Неравенства. Свойства числовых неравенств

1. НЕРАВЕНСТВА

2.

Число а больше числа b,
если разность а – b – положительное число
a > b, если а – b > 0
Число а меньше числа b,
если разность а – b – отрицательное число
a < b, если а – b < 0
Если а – b = 0, то а = b
На координатной прямой большее число
изображается точкой, лежащей правее, а
меньшее – точкой, лежащей левее

3.

1. Сформулируйте свойства числовых неравенств.
a b
a b, b c
a b, c любое число
a b и c 0
a b и c 0
a b, с d
a b, с d
a b, a 0, b 0
b a
a c
a с b с
ac bc
aс bc
a c b d
ac bd
n
a b
n

4.

2) - а > - b
3) 2b > 2а

5.

2. Известно, что a > b. Сравните a - b и b - a
1) a - b > b - a
2) a - b < b - a
3) a - b = b - a
4) Данных для сравнения недостаточно.
3.О числах a, b, c и d известно, что a b, b = c, d c.
Сравните d и a.
1) d = a
2) d a
3) d a
4) Сравнить невозможно.

6.

Неравенства бывают:
линейные
квадратные
рациональные
иррациональные

7. Вспомним:

Аналитическ
ая модель
х>а
х≥а
а≤ х < в
(а ; + ∞)
открытый луч
[а ; + ∞)
луч
открытый луч
в
(- ∞; в)
в
(- ∞; в]
луч
а
х≤в
а ≤х≤ в
Название
числовых
промежутков
а
х<в
а<х<в
Обозначение
Геометричес
кая модель
а
а
а
в
(а ; в)
интервал
в
[а ; в]
отрезок
полуинтервал
в
[а ; в)

8. Линейные неравенства

Определения:
1) Запись вида а>в; а≥в или а<в; а≤в называется
неравенством
2) Неравенства вида а≥в, а≤в называются
нестрогими.
3) Неравенства вида а>в, а<в называются
строгим
4) Решением неравенства с одной переменной
называется то значение переменной, которое
обращает его в верное числовое
неравенство

9. Линейные неравенства

Правила:
1) Любой член неравенства можно
переносить из одной части
неравенства в другую, изменив его
знак на противоположный, при этом
знак неравенства не изменится.

10. Линейные неравенства

Правила:
2) Обе части неравенства можно
умножить или разделить на одно и
тоже положительное число, при этом
знак неравенства не изменится.

11. Линейные неравенства

Правила:
3) Обе части неравенства можно
умножить или разделить на одно и
тоже отрицательное число, при этом
знак неравенства изменится на
противоположный.

12. Решим неравенство: 16х>13х+45

Решим неравенство: 16х>13х+45
Решение:
16х-13х > 45
слагаемое 13х с противоположным знаком
перенесли в левую часть неравенства
3х > 45
х > 15
15
привели подобные слагаемые
поделили обе части неравенства на 3
х
Ответ: (15;+∞)

13. Системы неравенств

• Система неравенств- это несколько неравенств
с одной переменной.
• Решение системы неравенств- это значение
переменной, при котором каждое из неравенств
системы обращается в верное числовое
неравенство.
• Общее решение неравенств- это множество
всех решений системы неравенств.

14.

5( х 1) 3( х 3) 1,
2х 1 х 1
7 2 .
Решить систему неравенств:
Решение. 1) Решим каждое неравенство данной системы:
5 х 5 3х 9 1,
2(2 х 1) 7( х 1);
2 х 5
3 х 9
: 2,
: (−3);
5 х 3х 10 5,
4 х 2 7 х 7;
х 2,5,
х 3.

15.

2) Изобразим решение каждого из
получившихся неравенств на одной числовой
прямой:
х 2,5,
||||||||||||||||||||||||||||||||||||||||||
/////////////////////////////////
х 3.
−3
2,5
−3 ≤ х ≤ 2,5.
3) Решение системы − отрезок [−3; 2,5]
Ответ: [−3; 2,5] .

16.

3 х 2 x 2,
2) Решить систему неравенств: х 15 6 2 x,
5 x 11 x 23.
Решение. 1) Решим каждое из неравенств данной системы
одновременно, получим:
3 х х 2 2,
х 2 х 6 15,
5 x х 23 11;
2 х 4
3 х 9
4 х 12
: 2,
: 3,
: 4;
х 2,
х 3,
х 3.
2) Изобразим решение каждого из
получившихся неравенств на одной числовой
прямой:

17.

х 2,
х 3,
х 3.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
////////////////////////////////
○ ○
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
−3 −2
3
−2< х ≤ 3.
3) Получили решение исходной системы: полуинтервал ( −2; 3]
Ответ:
(-2;3].

18.

КВАДРАТНЫЕ
НЕРАВЕНСТВА

19.

20. Квадратные неравенства

Определение: Квадратным называется
неравенство, левая часть которого −
квадратный трёхчлен, а правая часть
равна нулю:
ах²+bх+с>0
ах²+bх+с≥0
ах²+bх+с<0
ах²+bх+с≤0

21.

• Решением неравенства с одним
неизвестным называется то значение
неизвестного, при котором это
неравенство обращается в верное
числовое неравенство
• Решить неравенство − это значит
найти все его решения или
установить, что их нет.

22.

Квадратное неравенство
Алгоритм решения неравенств второй степени
(графический метод)
1. Приведите неравенство к виду ах2+вх+с>0 (ах2+вх+с <0)
2. Рассмотрите функцию у= ах2+вх+с
3. Определите направление ветвей
4. Найдите точки пересечения параболы с осью абсцисс (для
них у=0)
5. Схематически постройте график функции у=ах2+вх+с
6. Выделите часть параболы, для которой у>0 (у<0)
7. На оси абсцисс выделите те значения х, для которых у>0
(у<0)
8. Запишите ответ в виде промежутков

23.

Как может располагаться парабола у=ах2+bх+с
зависимости от поведения коэффициента a и
дискриминанта?
1) a>0
D>0
5) a>0
D<0
Х
Ветви ↑, две точки ∩ с Ох.
2) a<0
D>0
Ветви ↑, парабола не ∩ Ох.
Х
Ветви ↓, две точки ∩ с Ох.
3) a>0
D=0
6) a<0
D<0
Ветви ↓, парабола не ∩ Ох.
Х
Ветви ↑, парабола касается Ох.
4) a<0
D>0
Х
Х
Ветви ↓, парабола касается Ох.
Рассмотрим решение
квадратных неравенств
различных типов.
Х

24.

Алгоритм решения квадратного неравенства на
примере неравенства х 2 4 х 5 0 .
1) Введем функцию у х 2 4 х 5
2) Определим направление ветвей параболы. а < 0 - ветви
направлены вниз.
3) Найдем точки пересечения с
Ох: для этого решим
квадратное уравнение
х 2 4 х 5 0 x 1
x 5
-1
5
4) Схематично изобразим параболу.
5) Посмотрим на знак неравенства, выделим
соответствующие части графика и
соответствующие части Ох.
6) Ответ : x [ 1;5 ]
06.12.2023
Х
24

25.

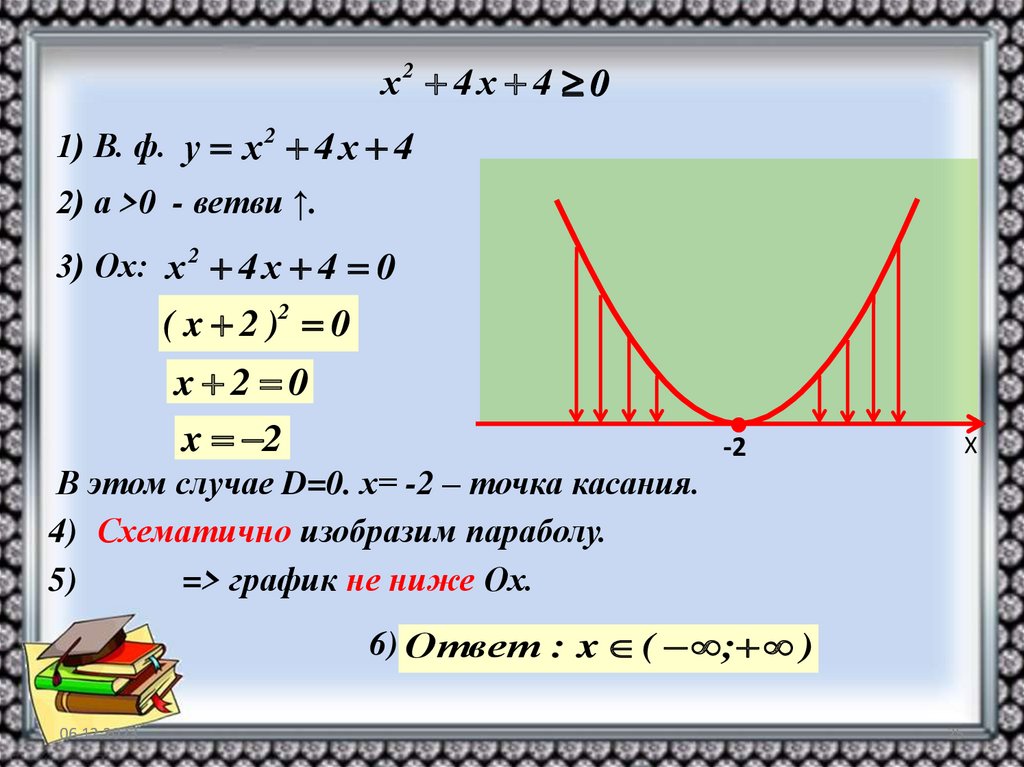
х2 4 х 4 0
1) В. ф. у х 2 4 х 4
2) а >0 - ветви ↑.
3) Ох: х 2 4 х 4 0
( x 2 )2 0
x 2 0
x 2
-2
Х
В этом случае D=0. х= -2 – точка касания.
4) Схематично изобразим параболу.
5)
=> график не ниже Ох.
6) Ответ : x ( ; )
06.12.2023
25

26.

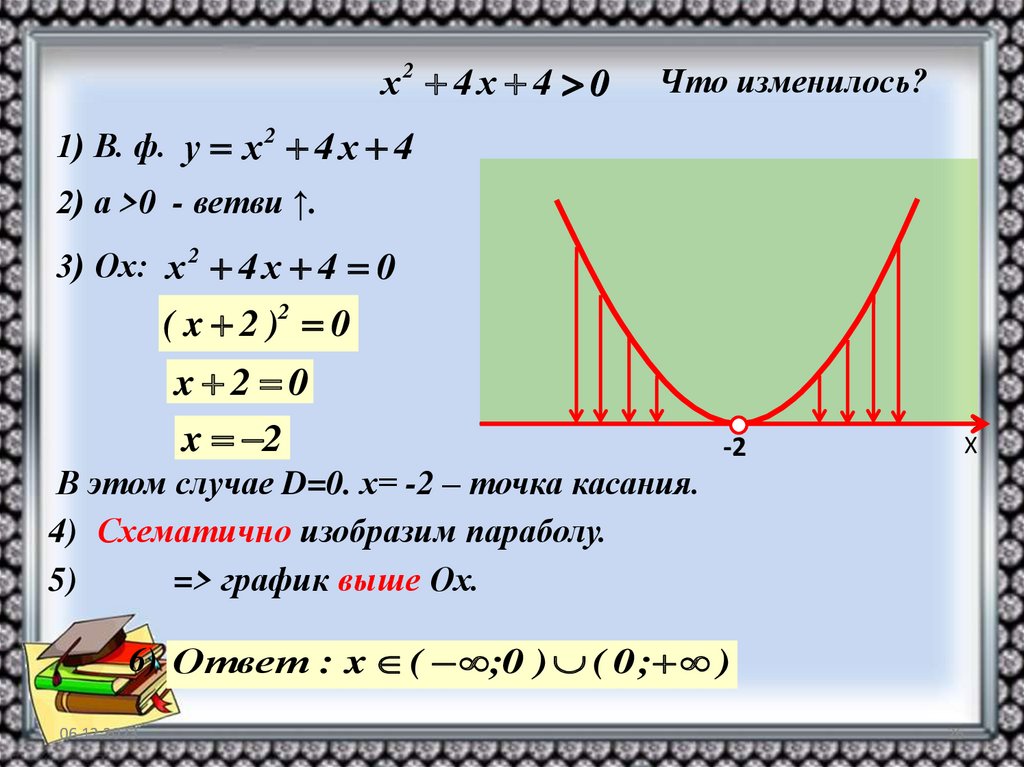
х2 4 х 4 0
Что изменилось?
1) В. ф. у х 2 4 х 4
2) а >0 - ветви ↑.
3) Ох: х 2 4 х 4 0
( x 2 )2 0
x 2 0
x 2
-2
Х
В этом случае D=0. х= -2 – точка касания.
4) Схематично изобразим параболу.
5)
=> график выше Ох.
6) Ответ : x ( ;0 ) ( 0 ; )
06.12.2023
26

27.

х2 4 х 4 0
Что изменилось?
1) В. ф. у х 2 4 х 4
2) а >0 - ветви ↑.
3) Ох: х 2 4 х 4 0
( x 2 )2 0
x 2 0
x 2
-2
Х
В этом случае D=0. х= -2 – точка касания.
4) Схематично изобразим параболу.
5)
=> график не выше Ох.
Не выше Ох нет есть одна точка.
6) Ответ : x 2
06.12.2023
27

28.

х2 4 х 4 0
Что изменилось?
1) В. ф. у х 2 4 х 4
2) а >0 - ветви ↑.
3) Ох: х 2 4 х 4 0
( x 2 )2 0
x 2 0
x 2
-2
Х
В этом случае D=0. х= -2 – точка касания.
4) Схематично изобразим параболу.
5)
=> график ниже Ох.
Ниже Ох нет ни одной точки.
6) Ответ : Ø
06.12.2023
28

29.

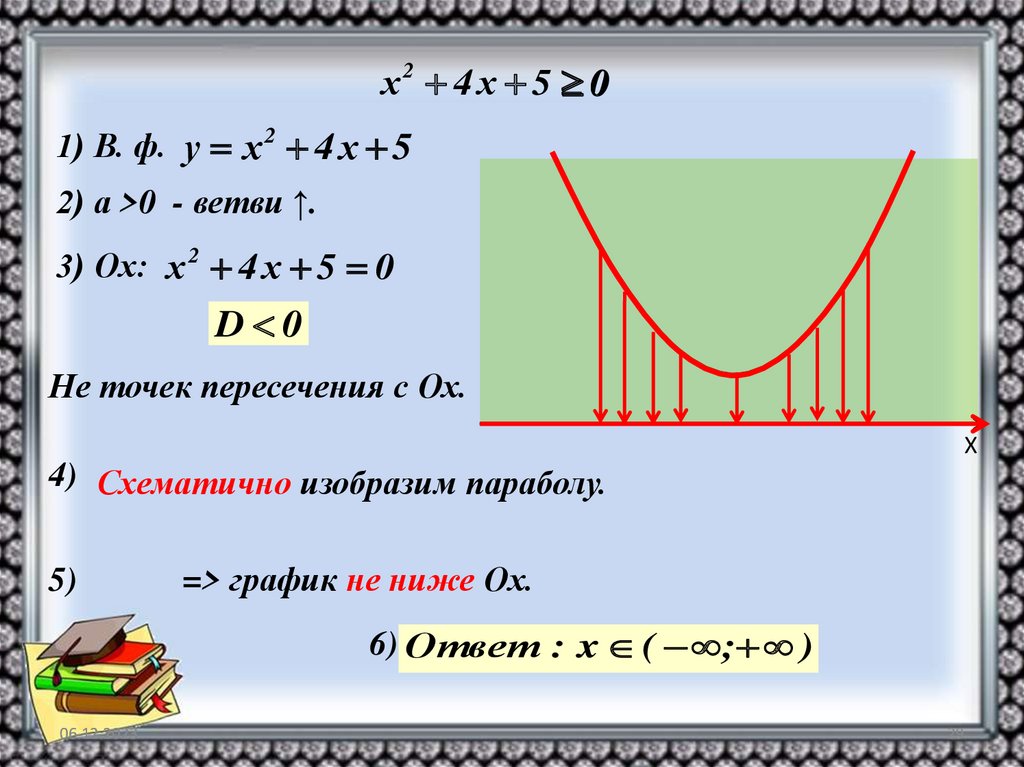
х2 4 х 5 0
1) В. ф. у х 2 4 х 5
2) а >0 - ветви ↑.
3) Ох: х 2 4 х 5 0
D 0
Не точек пересечения с Ох.
Х
4) Схематично изобразим параболу.
5)
=> график не ниже Ох.
6) Ответ : x ( ; )
06.12.2023
29

30.

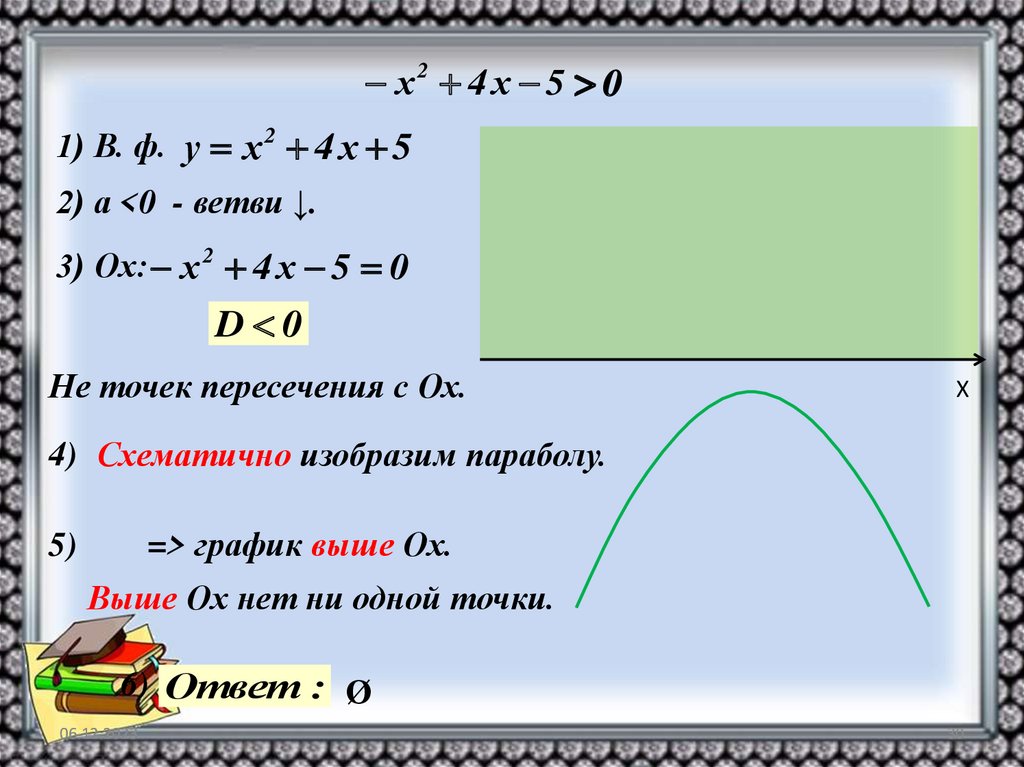
х2 4 х 5 0
1) В. ф. у х 2 4 х 5
2) а <0 - ветви ↓.
3) Ох: х 2 4 х 5 0
D 0
Не точек пересечения с Ох.
Х
4) Схематично изобразим параболу.
=> график выше Ох.
5)
Выше Ох нет ни одной точки.
6) Ответ : Ø
06.12.2023
30