Похожие презентации:
Общее по теме стереометрии (лекция 21)
1. Лекция 21. Общее по теме стереометрии
hS1
S2
S3
2.
Свойства плоских фигур,известные из курса планиметрии
имеют место и в стереометрии
(теоремы о равенстве и подобии
треугольников,
свойство углов с соответственно
параллельными сторонами и
т.д.).
3. Аксиоматический метод:
1. Перечисляются основныенеопределяемые понятия.
2. Формулируются аксиомы,
описывающие свойства основных
понятий.
3. С помощью основных понятий даются
определения более сложных понятий.
4. На основе введенных понятий (как
основных, так и прочих) и аксиом
доказываются теоремы.
4. 1. Перечисляются основные неопределяемые понятия
Основные понятия планиметрии:точка,
прямая,
расстояние.
Эти понятия, являясь идеальными
геометрическими объектами, возникли
вследствие отвлечения от всего
несущественного и случайного в реальных
физических объектах окружающего нас мира и
их отношениях.
Например, точка является идеализацией
свойств таких реальных объектов как песчинка,
острие иглы, . . . , а прямая — луча света,
натянутой нити и т.д.
5. В стереометрии
имеется четыре основных понятия:точка,
прямая,
расстояние,
плоскость.
6. 2. Формулируются аксиомы
Аксиомы – утверждения,принимаемые без доказательства,
отражают тем не менее реальные свойства
объектов окружающего мира, послуживших
«прообразами» основных понятий геометрии.
Так, например, аксиома планиметрии: «Через
любые две точки можно провести
единственную прямую» отражает наглядное
свойство:
сколько бы раз мы ни направляли луч света из
одной фиксированной точки в другую, он будет
описывать одну и ту же прямолинейную
траекторию.
7. 3. Даются определения более сложных понятий
Так, используя основныегеометрические понятия точки и
расстояния, определена окружность
как множество точек плоскости,
удаленных на одно и то же расстояние
(радиус) от фиксированной точки
(центра).
Подобным же образом определялись
отрезок, треугольник и другие понятия.
8. 4. На основе введенных понятий и аксиом доказываются теоремы
Все теоремы геометрии, каки других разделов
математики, доказываются с
помощью строгих логических
рассуждений
(признаки равенства
треугольников, теоремы Пифагора и
Фалеса и т.д.)
9. Заметим, что
для любой плоскостипространства справедливы
все основные определения,
выводы и аксиомы
планиметрии!!!
10. Аксиомы стереометрии Аксиома 1 (аксиома плоскости):
В пространстве существуютразличные плоскости.
Через любые три точки,
не лежащие на одной прямой,
проходит единственная
плоскость.
Из этой аксиомы вытекает, что пространство
состоит из бесконечного множества точек
(так как множество точек плоскости бесконечно),
не совпадающего ни с какой плоскостью, и
значит, для любой плоскости найдутся точки,
не принадлежащие ей.
11. Аксиома 2 (аксиома прямой и плоскости ):
Если две различныеα
точки прямой
принадлежат плоскости, ∙A
то и все точки прямой
принадлежат этой
плоскости.
∙B
l
Таким образом, прямая, не принадлежащая целиком
данной плоскости, может иметь с ней не более
одной общей точки.
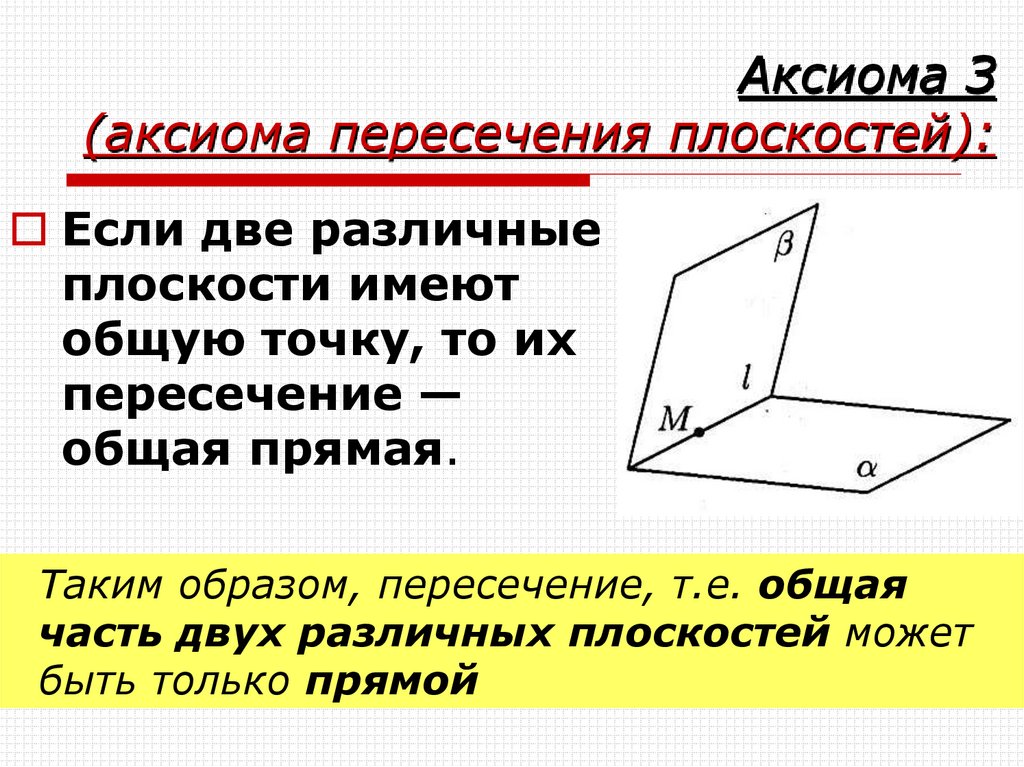
12. Аксиома З (аксиома пересечения плоскостей):
Если две различныеплоскости имеют
общую точку, то их
пересечение —
общая прямая.
Таким образом, пересечение, т.е. общая
часть двух различных плоскостей может
быть только прямой
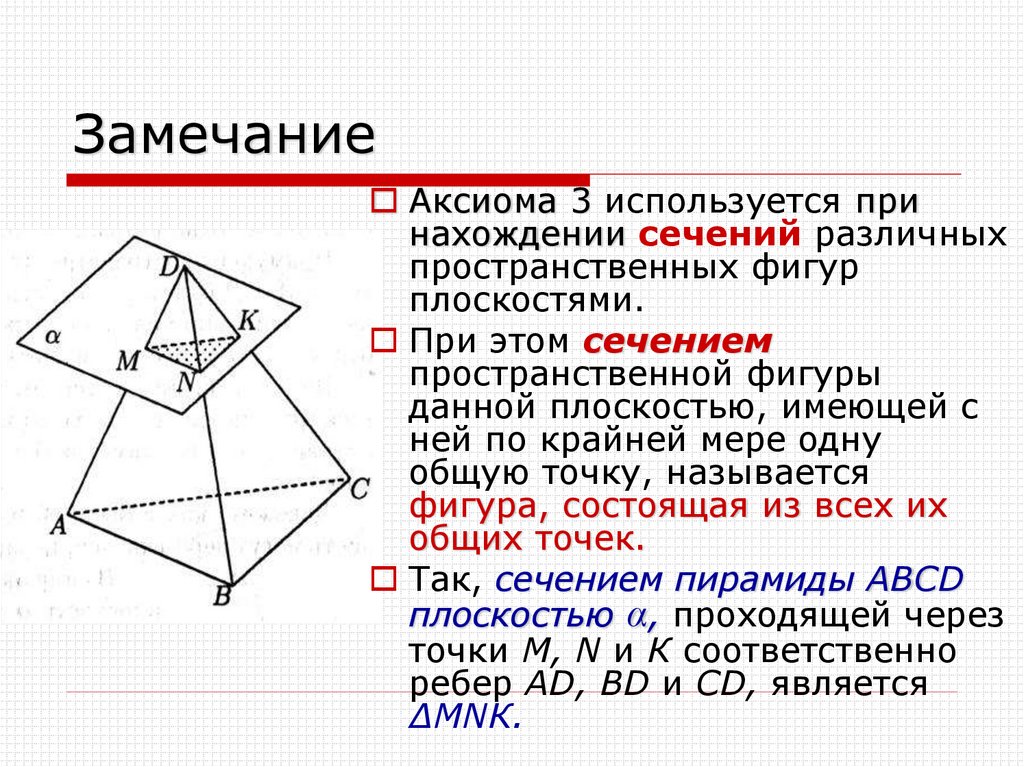
13. Замечание
Аксиома 3 используется принахождении сечений различных
пространственных фигур
плоскостями.
При этом сечением
пространственной фигуры
данной плоскостью, имеющей с
ней по крайней мере одну
общую точку, называется
фигура, состоящая из всех их
общих точек.
Так, сечением пирамиды АВСD
плоскостью α, проходящей через
точки М, N и К соответственно
ребер АD, ВD и СD, является
∆МNК.
14. Свойства прямой в пространстве
∙A∙B
(AB)
1. Через любые две различные точки
пространства проходит
единственная прямая.
Прямую в пространстве, проходящую
через две различные точки А и В будем
обозначать (АВ). То же будет обозначать
выражение «прямая АВ».
Отрезок с концами в точках А и В будем,
как и ранее, обозначать АВ.
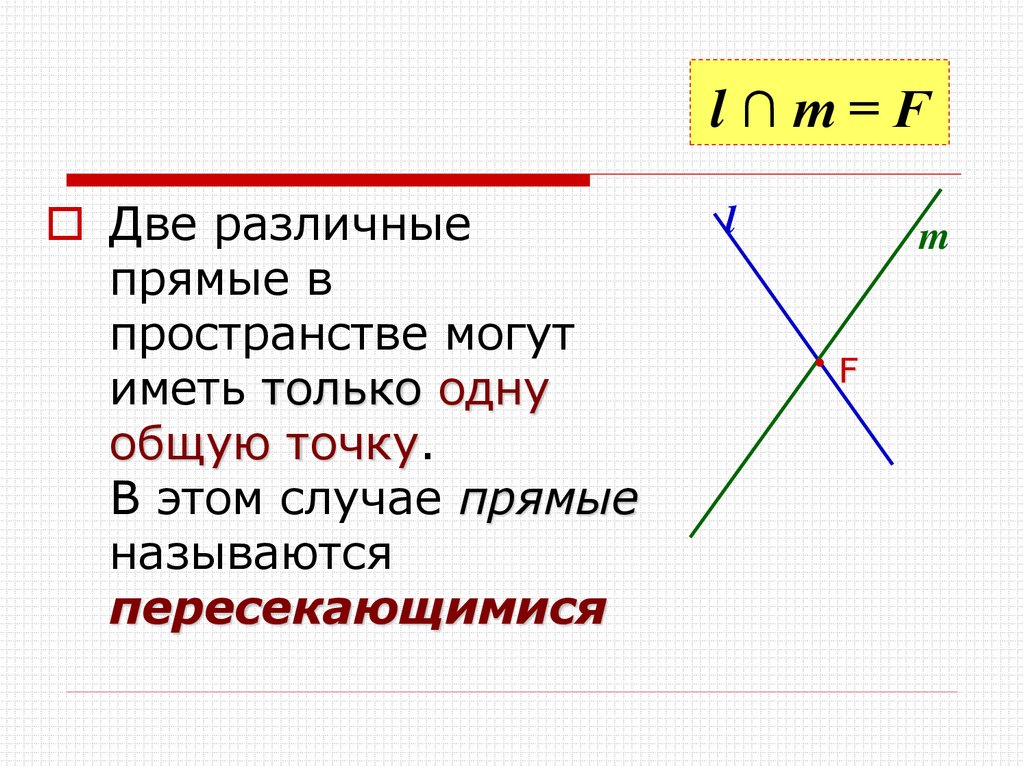
15. l ∩ m = F
l∩m=FДве различные
прямые в
пространстве могут
иметь только одну
общую точку.
В этом случае прямые
называются
пересекающимися
l
m
F
16. Прямая и плоскость могут пересекаться, т.е. иметь только одну общую точку.
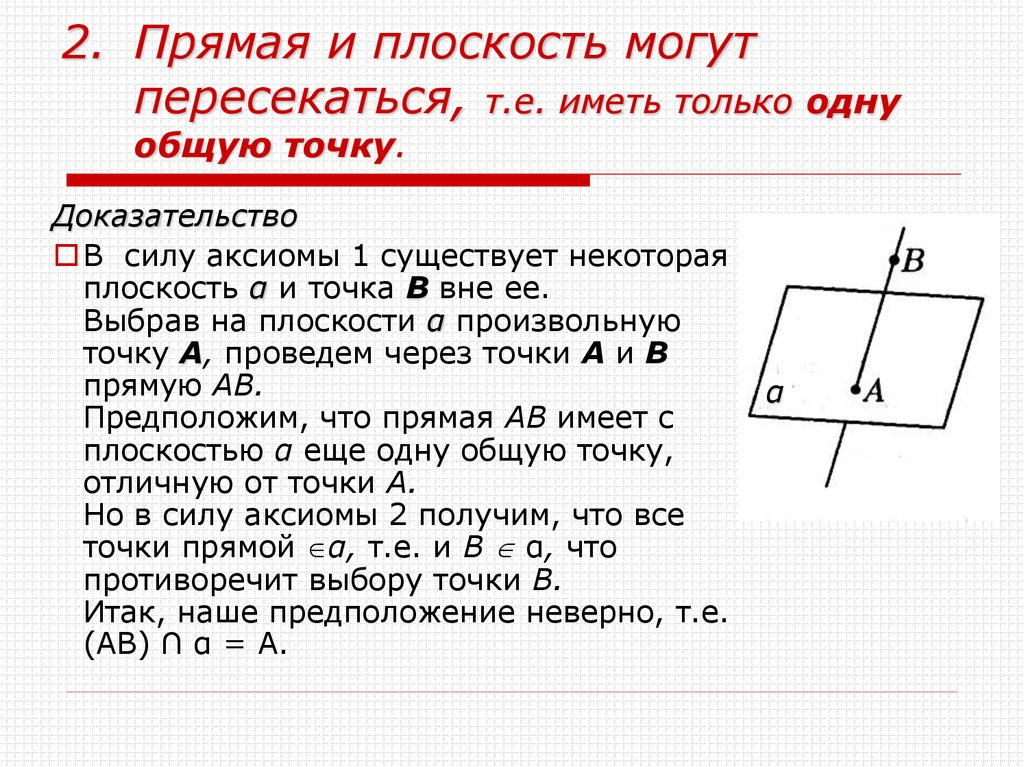
2. Прямая и плоскость могутпересекаться, т.е. иметь только одну
общую точку.
Доказательство
В силу аксиомы 1 существует некоторая
плоскость α и точка В вне ее.
Выбрав на плоскости α произвольную
точку А, проведем через точки А и В
прямую АВ.
Предположим, что прямая АВ имеет с
плоскостью α еще одну общую точку,
отличную от точки А.
Но в силу аксиомы 2 получим, что все
точки прямой α, т.е. и В α, что
противоречит выбору точки В.
Итак, наше предположение неверно, т.е.
(АВ) ∩ α = А.
α
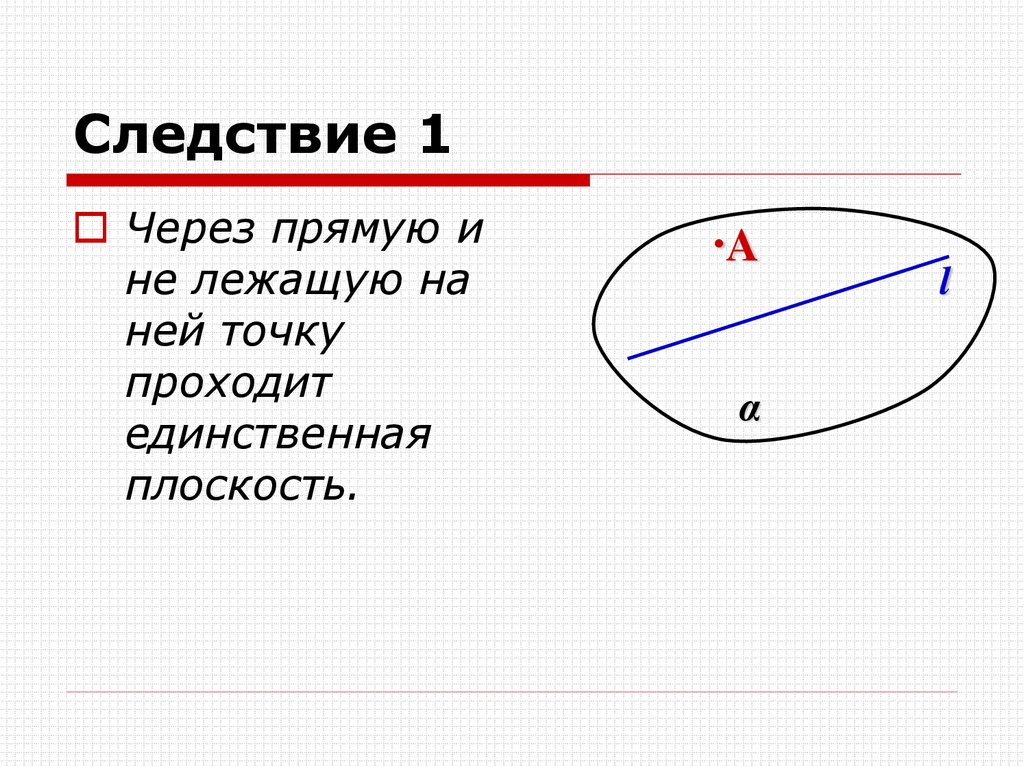
17. Следствие 1
Через прямую ине лежащую на
ней точку
проходит
единственная
плоскость.
∙A
α
l
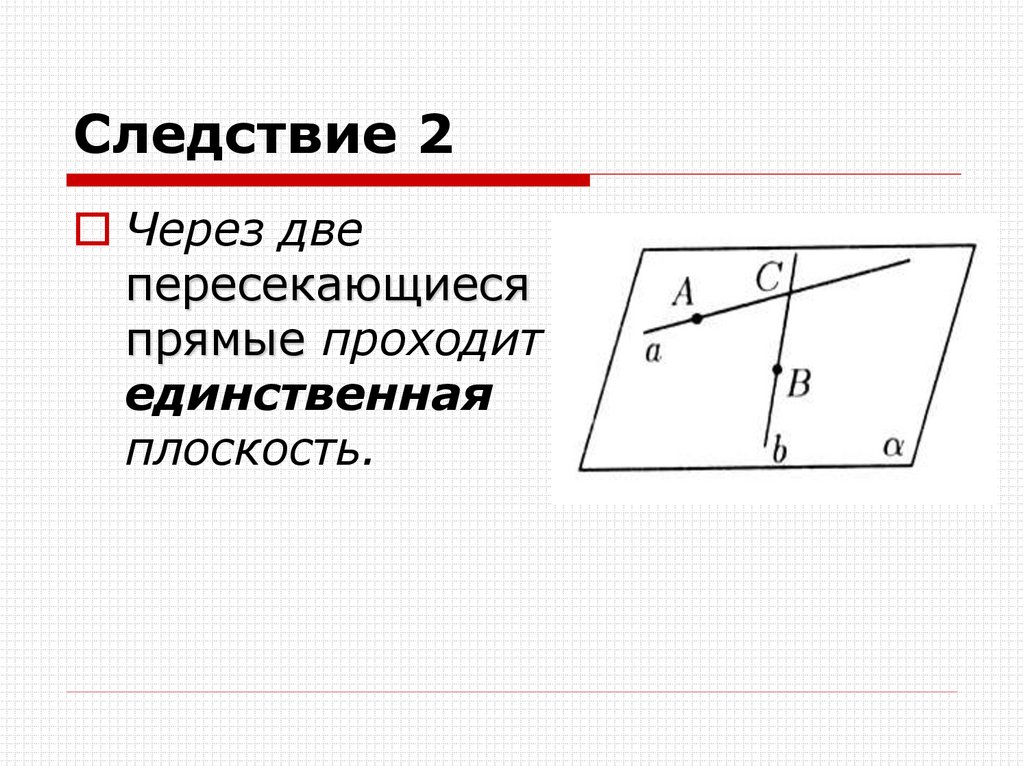
18. Следствие 2
Через двепересекающиеся
прямые проходит
единственная
плоскость.
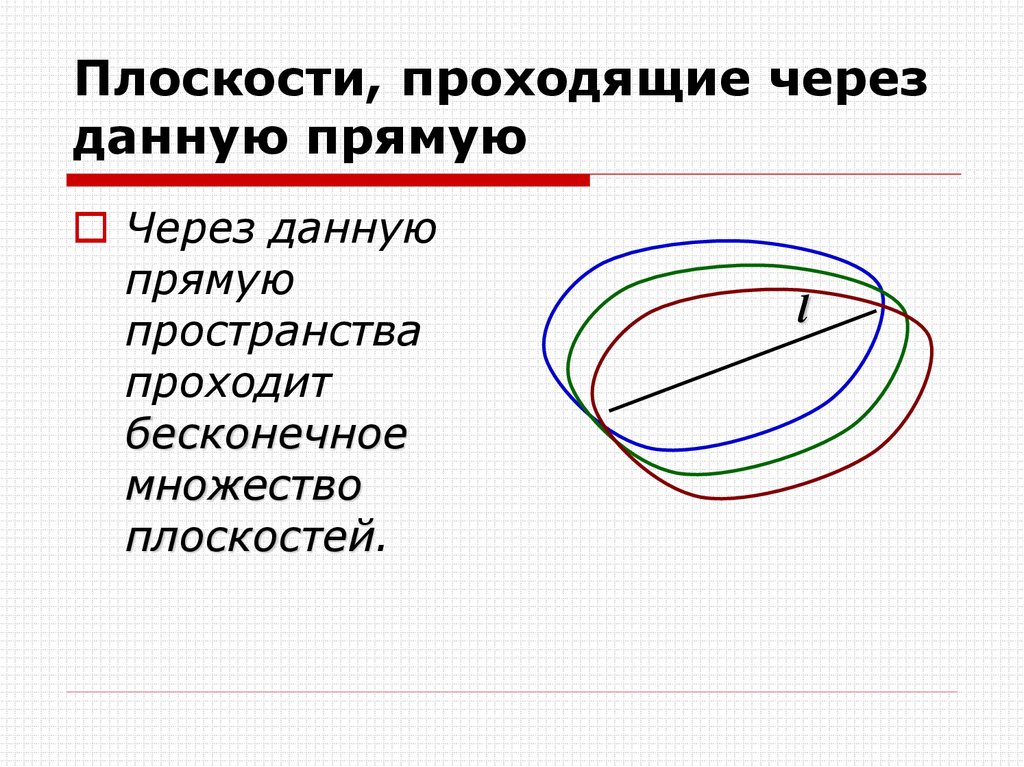
19. Плоскости, проходящие через данную прямую
Через даннуюпрямую
пространства
проходит
бесконечное
множество
плоскостей.
l
20. Характеристическое свойство прямой, плоскости и пространства
если фигура в пространстве,отличная от точки, обладает тем
свойством, что прямая, соединяющая
любые две точки этой фигуры,
целиком принадлежит ей,
то данная фигура является
- или прямой,
- или плоскостью,
- или совпадает со всем
пространством.
21. Аксиома 4 (аксиома расстояния):
Для любых двух точек А и В и пространстваоднозначно определено некоторое
неотрицательное число |АВ|, называемое
расстоянием между ними и обладающее
следующими свойствами:
|АВ| = |ВА|
|АВ| = 0 тогда и только тогда, когда
точки А и В совпадают;
|АС| ≤ |АВ| + |BС|, причем равенство
достигается в том и только в том случае, когда
точка В принадлежит отрезку АС.
Обозначение: |АВ| — расстояние между точками А и В;
АВ – длина отрезка АВ.
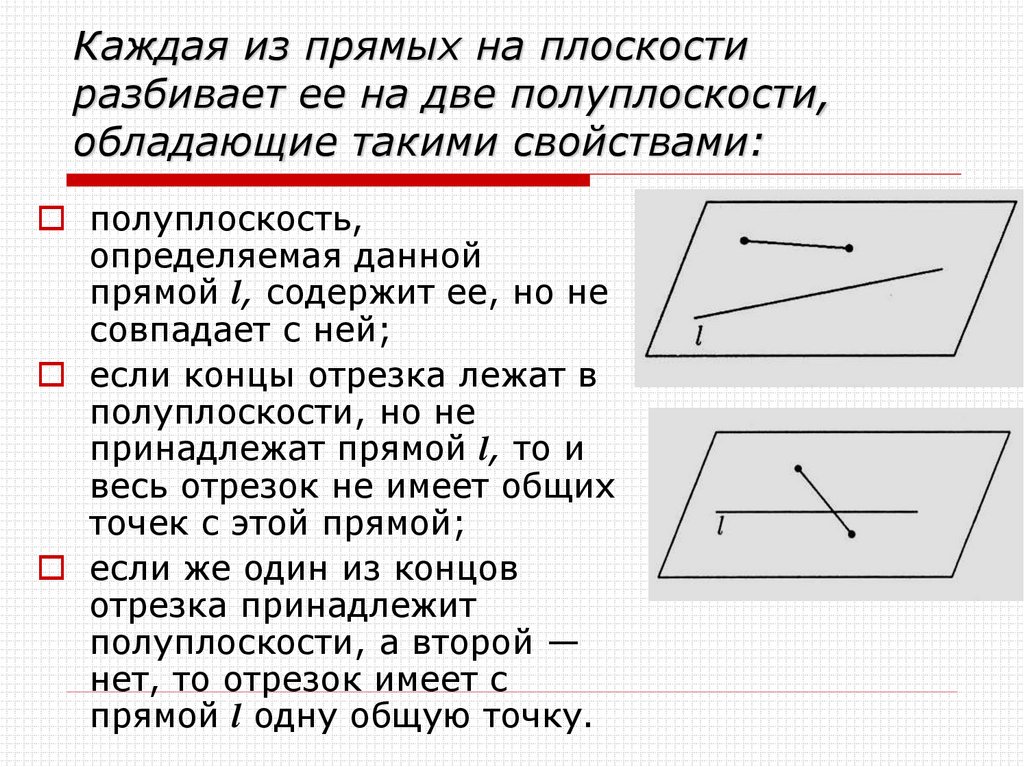
22. Каждая из прямых на плоскости разбивает ее на две полуплоскости, обладающие такими свойствами:
полуплоскость,определяемая данной
прямой l, содержит ее, но не
совпадает с ней;
если концы отрезка лежат в
полуплоскости, но не
принадлежат прямой l, то и
весь отрезок не имеет общих
точек с этой прямой;
если же один из концов
отрезка принадлежит
полуплоскости, а второй —
нет, то отрезок имеет с
прямой l одну общую точку.
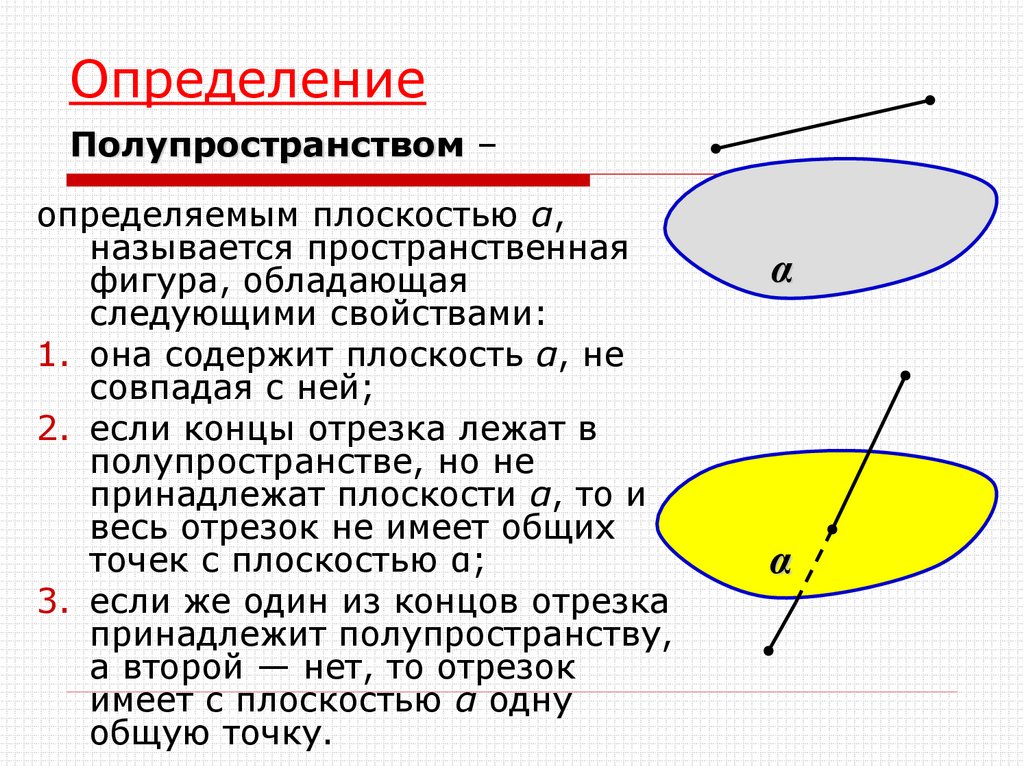
23. Определение Полупространством –
определяемым плоскостью α,называется пространственная
фигура, обладающая
следующими свойствами:
1. она содержит плоскость α, не
совпадая с ней;
2. если концы отрезка лежат в
полупространстве, но не
принадлежат плоскости α, то и
весь отрезок не имеет общих
точек с плоскостью α;
3. если же один из концов отрезка
принадлежит полупространству,
а второй — нет, то отрезок
имеет с плоскостью α одну
общую точку.
α
α
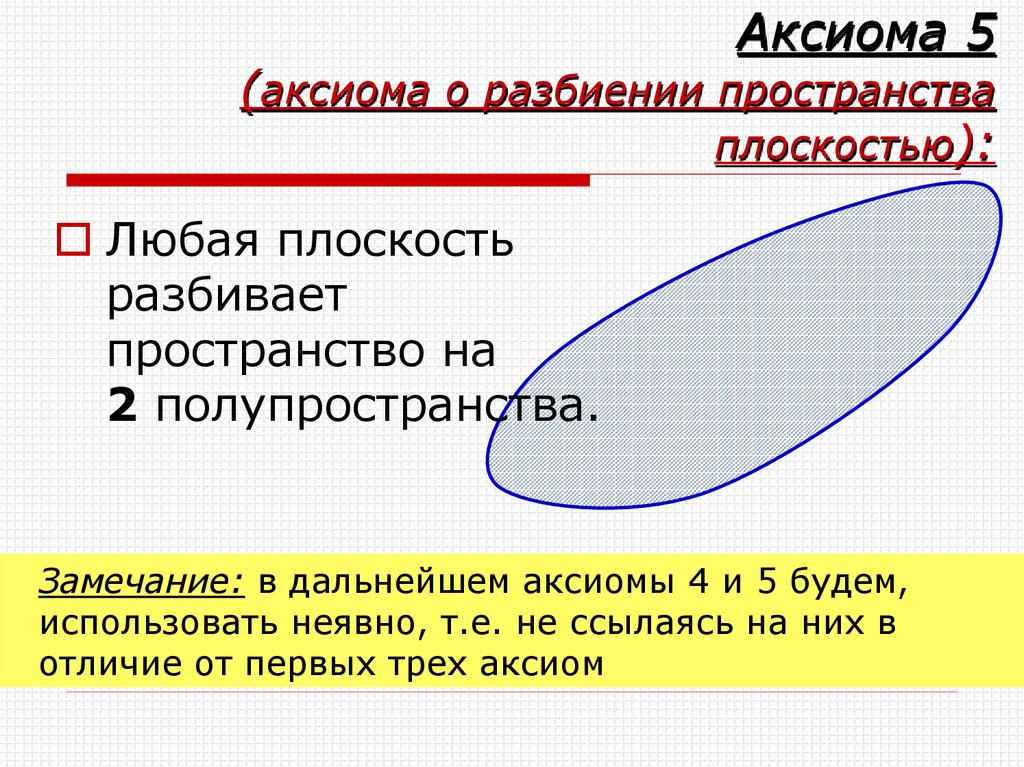
24. Аксиома 5 (аксиома о разбиении пространства плоскостью):
Любая плоскостьразбивает
пространство на
2 полупространства.
Замечание: в дальнейшем аксиомы 4 и 5 будем,
использовать неявно, т.е. не ссылаясь на них в
отличие от первых трех аксиом
25. УПРАЖНЕНИЯ для ума… 1 вариант 2 вариант
1.Приведитепримеры
пространственных
фигур, плоских
фигур, неплоских
фигур.
Какое минимальное
число точек может
содержать
неплоская фигура?
1.Перечислите
основные понятия
стереометрии.
Попытайтесь дать
определение шара,
укажите основные
понятия,
используемые в этом
определении.
26. УПРАЖНЕНИЯ для ума… 1 вариант 2 вариант
2.Верно ли, что черезтри попарно
пересекающиеся
прямые проходит
единственная
плоскость?
2.Верно ли, что можно
провести плоскость
через любые:
а) две точки,
б) три точки,
в) четыре точки?
27. УПРАЖНЕНИЯ для ума… 1 вариант 2 вариант
3.Укажите различныеспособы задания
плоскостей.
Верно ли, что через
любые два отрезка,
имеющих по
крайней мере одну
общую точку,
проходит
единственная
плоскость?
3.Дайте определение
полупространства.
Почему все
пространство не
может быть
полупространством,
определяемым
некоторой
плоскостью α ?
28. УПРАЖНЕНИЯ для ума… 1 вариант 2 вариант
УПРАЖНЕНИЯ для ума…1 вариант
4.Совпадает ли
плоскость, в которой
лежит трапеция с
плоскостью,
проходящей через:
а) середины ее
боковых сторон?
2 вариант
4.Совпадает ли
плоскость, в
которой лежит
трапеция с
плоскостью,
проходящей
через:
а) середины всех
сторон трапеции?
29. УПРАЖНЕНИЯ для ума… 1 вариант 2 вариант
5.Могут ли три5.Могут ли три
различные плоскости
различные плоскости
пересекаться только:
пересекаться только:
а) в одной точке;
а) в двух точках;
б) по двум
б) по двум
пересекающимся
пересекающимся
прямым?
прямым?


















 Математика
Математика








