Предмет стереометрии. Аксиомы стереометрии и следствия из них

1. Предмет стереометрии. Аксиомы стереометрии и следствия из них.

Урок-лекция

2.

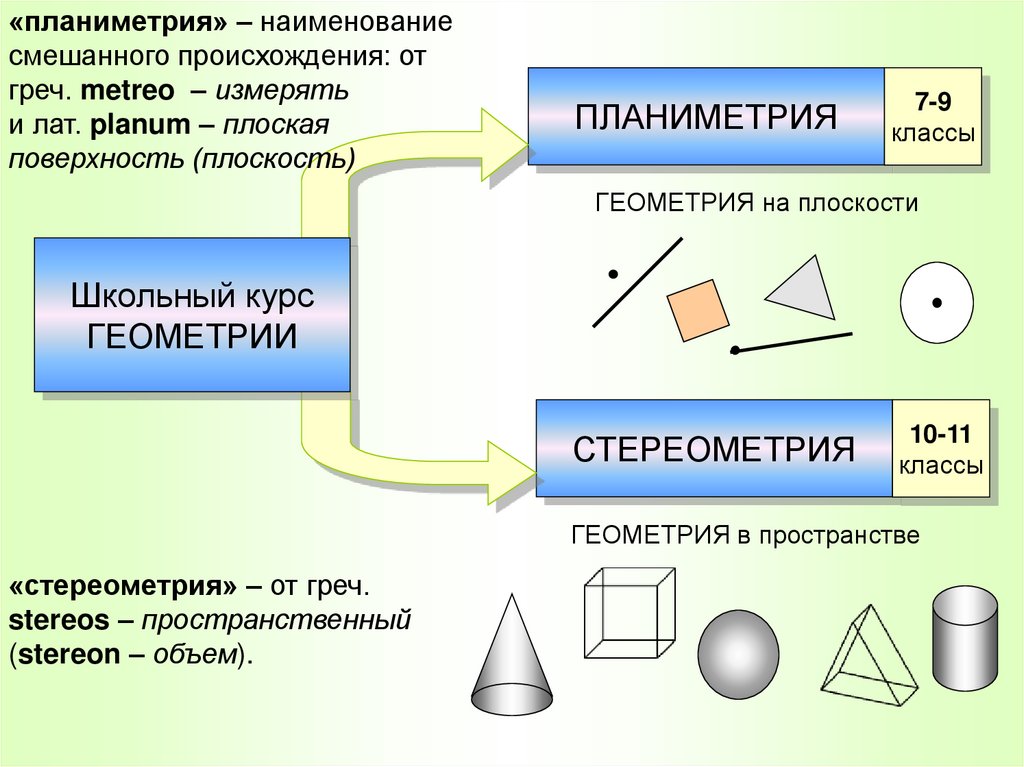
«планиметрия» – наименование
смешанного происхождения: от
греч. metreo – измерять
и лат. planum – плоская
поверхность (плоскость)
ПЛАНИМЕТРИЯ
7-9
классы
ГЕОМЕТРИЯ на плоскости
Школьный курс
ГЕОМЕТРИИ
СТЕРЕОМЕТРИЯ
10-11
классы
ГЕОМЕТРИЯ в пространстве
«стереометрия» – от греч.
stereos – пространственный
(stereon – объем).

3.

Геометрия
Наука, которая изучает свойства
геометрических фигур
Планиметрия
Стереометрия
Раздел геометрии, в котором
изучаются свойства фигур
на плоскости
Раздел геометрии, в котором
изучаются свойства фигур
в пространстве

4. Мы знаем, что

ГЕОМЕТРИЯ возникла из
практических задач людей;
ГЕОМЕТРИЯ лежит в основе всей
техники и большинства изобретений
технику,
человечества;
инженеру,
ГЕОМЕТРИЯ нужна
рабочему,
архитектору,
модельеру …

5. Изучая СТЕРЕОМЕТРИЮ

Мы проведем систематическое рассмотрение
свойств геометрических тел в пространстве.
Освоим различные способы вычисления
практически важных геометрических величин.
При этом мы будем развивать
пространственное воображение и логическое
мышление

6.

Геометрические фигуры
в пространстве
называют телами

7.

Одна и та же
фигура допускает
различные
изображения

8.

Изображения
пространственных фигур
Куб
Шар
Параллелепипед
Конус
Пирамида
Цилиндр

9.

При изучении стереометрии мы будем пользоваться рисунками,
чертежами: они помогут нам понять, представить,
проиллюстрировать содержание того или иного факта.
Поэтому прежде, чем приступить к пониманию сущности аксиомы,
определения, доказательству теоремы, решению геометрической
задачи, постарайтесь наглядно представить, вообразить,
нарисовать фигуры, о которых идет речь .
«Мой карандаш, бывает еще
остроумней моей головы», —
признавался великий математик
Леонард Эйлер (1707—1783).
ВЫВОД:
Интуитивное, живое пространственное воображение в сочетании со
строгой логикой мышления — это ключ к изучению стереометрии

10.

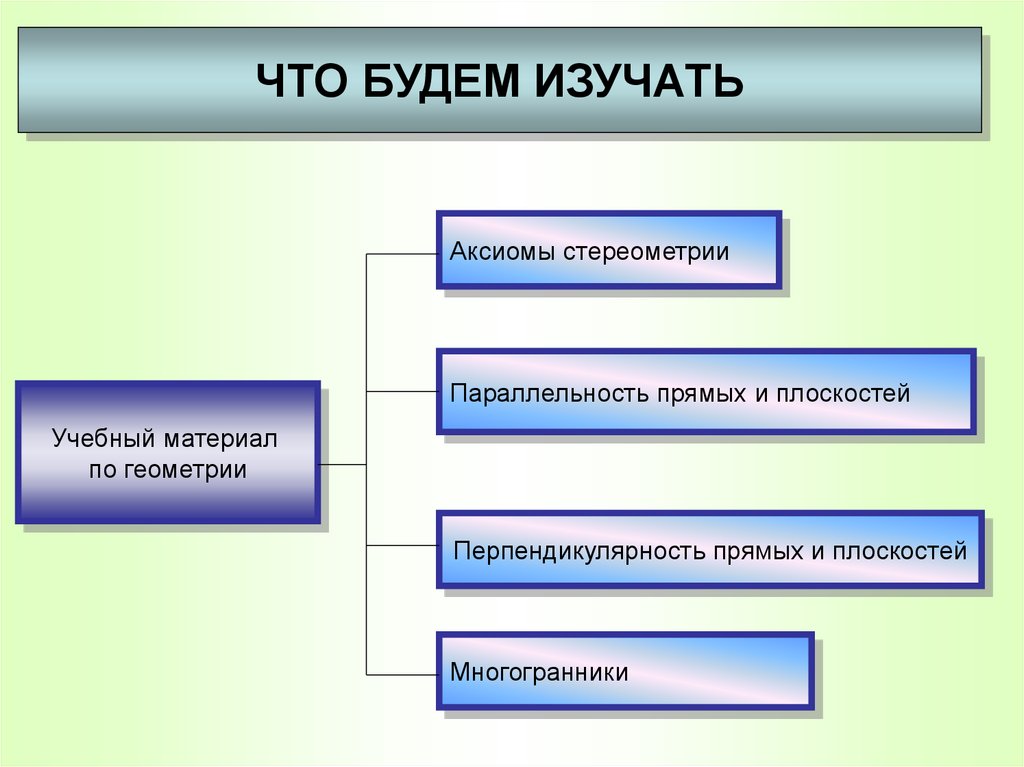
ЧТО БУДЕМ ИЗУЧАТЬ
Аксиомы стереометрии
Параллельность прямых и плоскостей
Учебный материал
по геометрии
Перпендикулярность прямых и плоскостей
Многогранники

11. Основные понятия стереометрии

точка,
прямая,
плоскость,
расстояние
А
Р
A , KC , P
С
К
, |PK| = 2 см
= (РКС)
|PK|

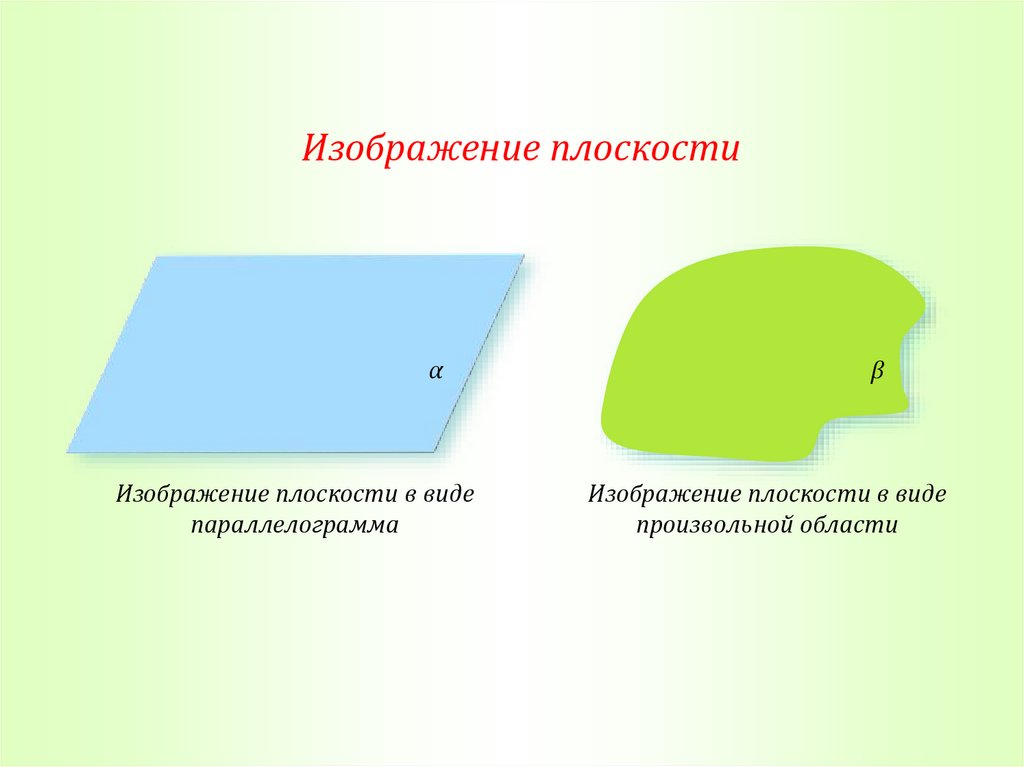
12.

Изображение плоскости
α
Изображение плоскости в виде
параллелограмма
β
Изображение плоскости в виде
произвольной области

13.

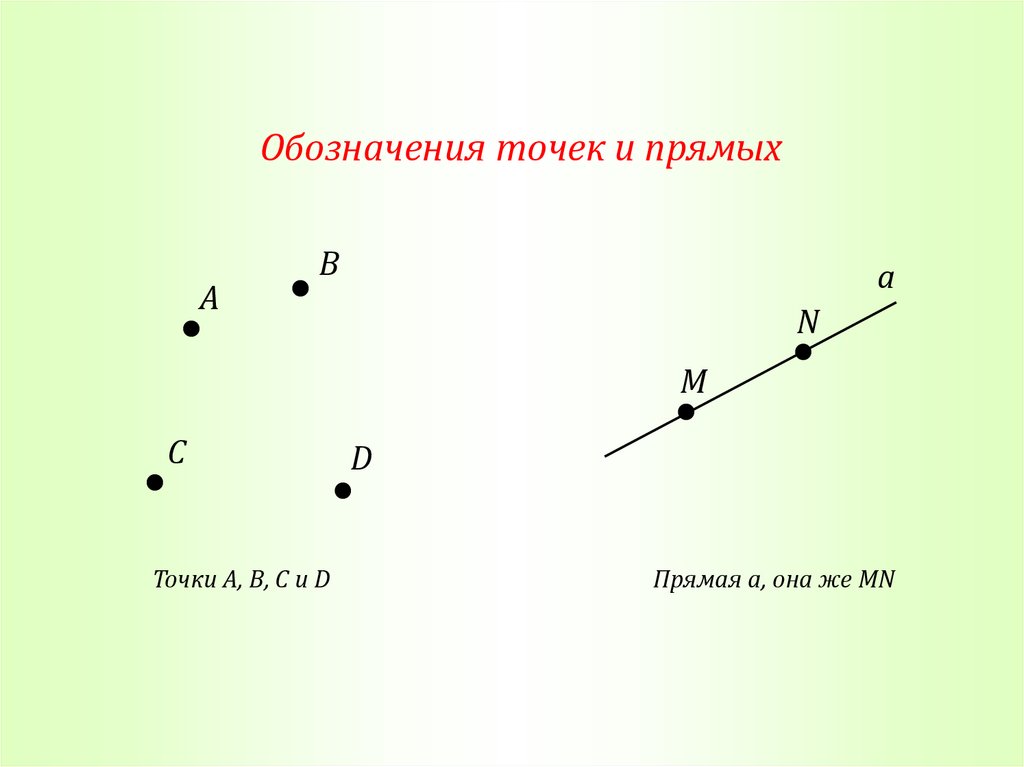
Обозначения точек и прямых
A
B
a
N
M
C
Точки A, B, C и D
D
Прямая a, она же MN

14.

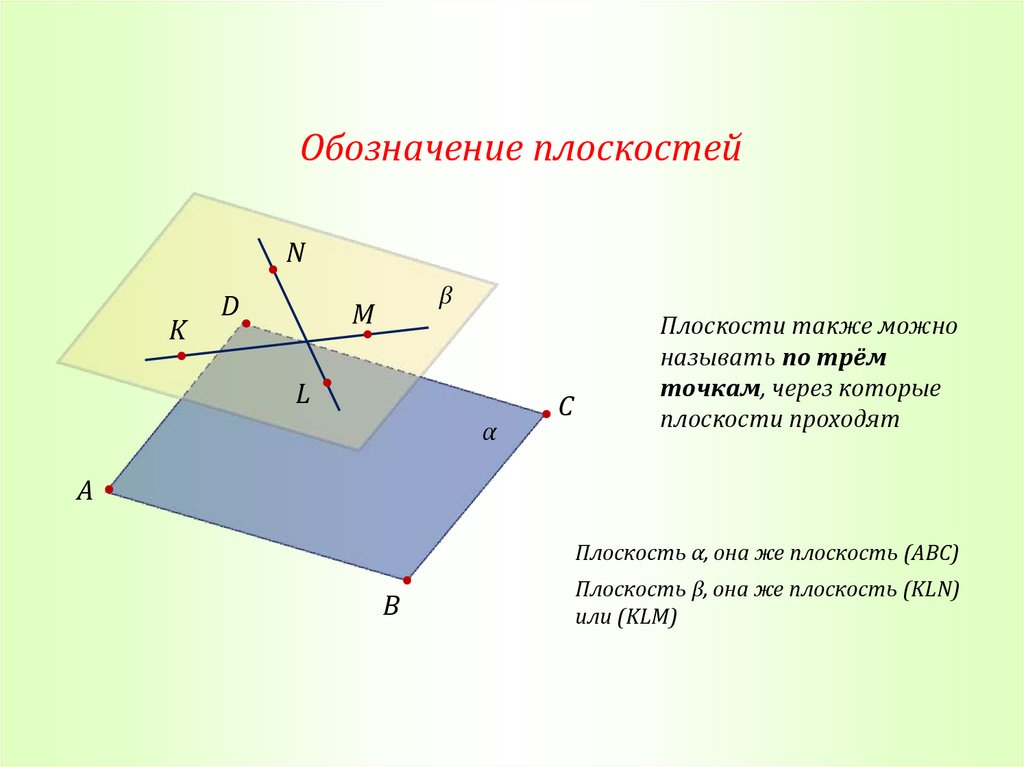
Обозначение плоскостей
N
K
D
β
M
L
α
C
Плоскости также можно
называть по трём
точкам, через которые
плоскости проходят
A
Плоскость α, она же плоскость (ABC)
B
Плоскость β, она же плоскость (KLN)
или (KLM)

15.

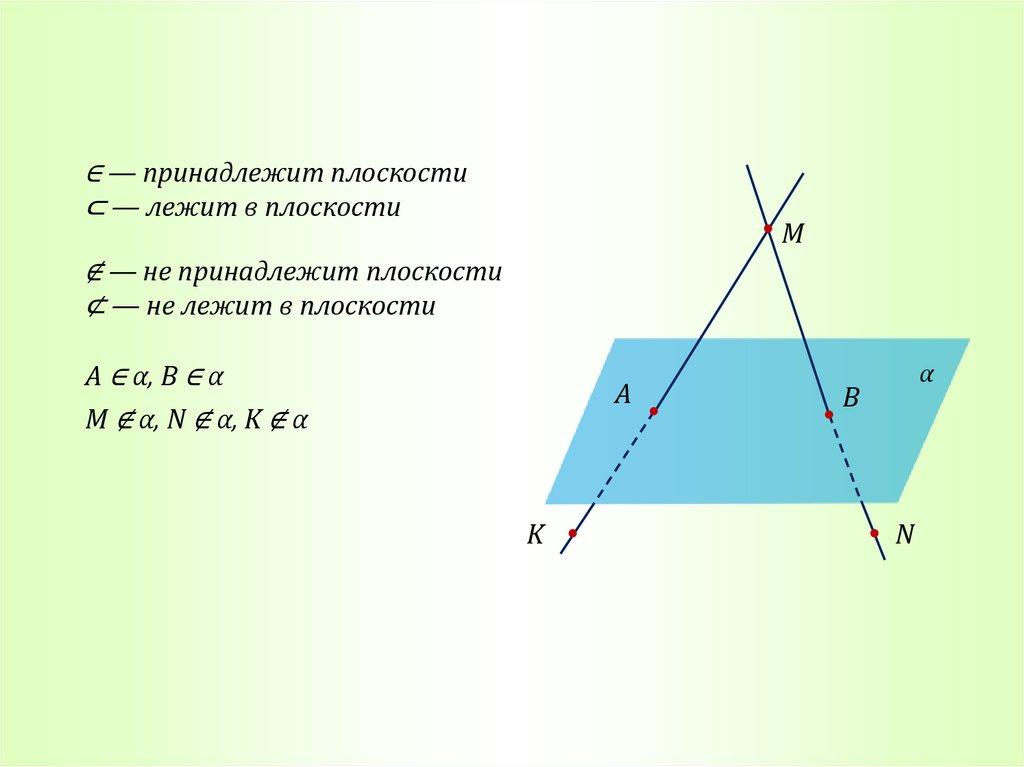
∈ — принадлежит плоскости
⊂ — лежит в плоскости
M
∉ — не принадлежит плоскости
⊄ — не лежит в плоскости
A ∈ α, B ∈ α
M ∉ α, N ∉ α, K ∉ α
A
K
α
B
N

16.

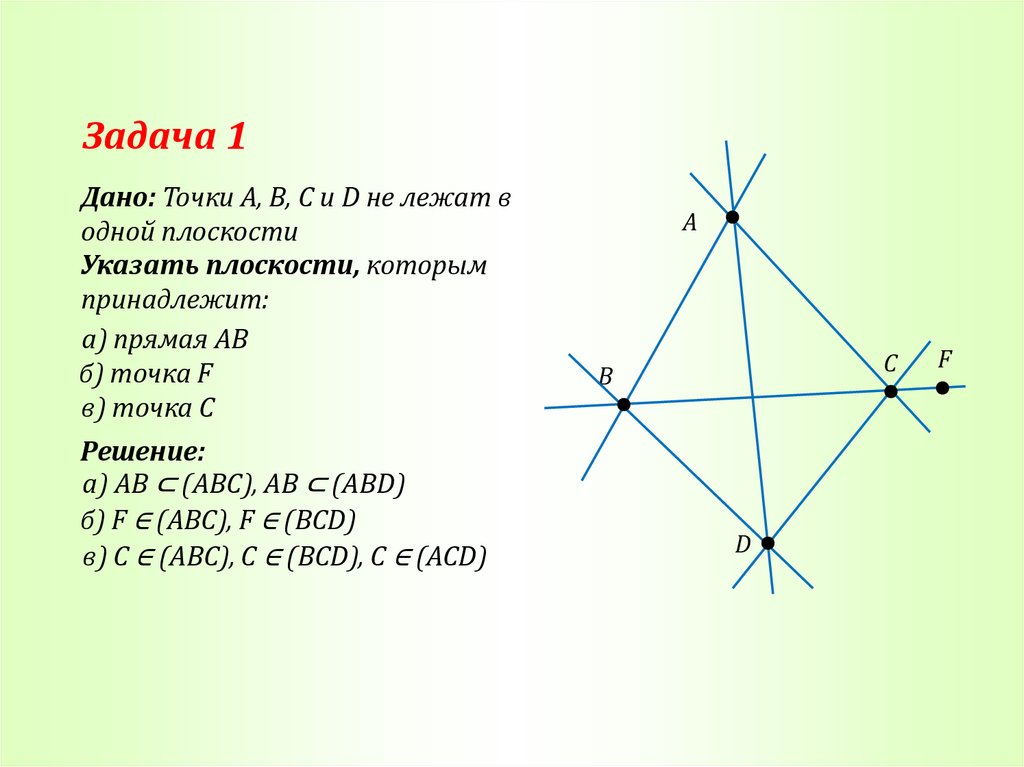
Задача 1
Дано: Точки A, B, C и D не лежат в
одной плоскости
Указать плоскости, которым
принадлежит:
а) прямая AB
б) точка F
в) точка C
Решение:
а) AB ⊂ (ABC), AB ⊂ (ABD)
б) F ∈ (ABC), F ∈ (BCD)
в) C ∈ (ABC), C ∈ (BCD), C ∈ (ACD)
A
C
B
D
F

17.

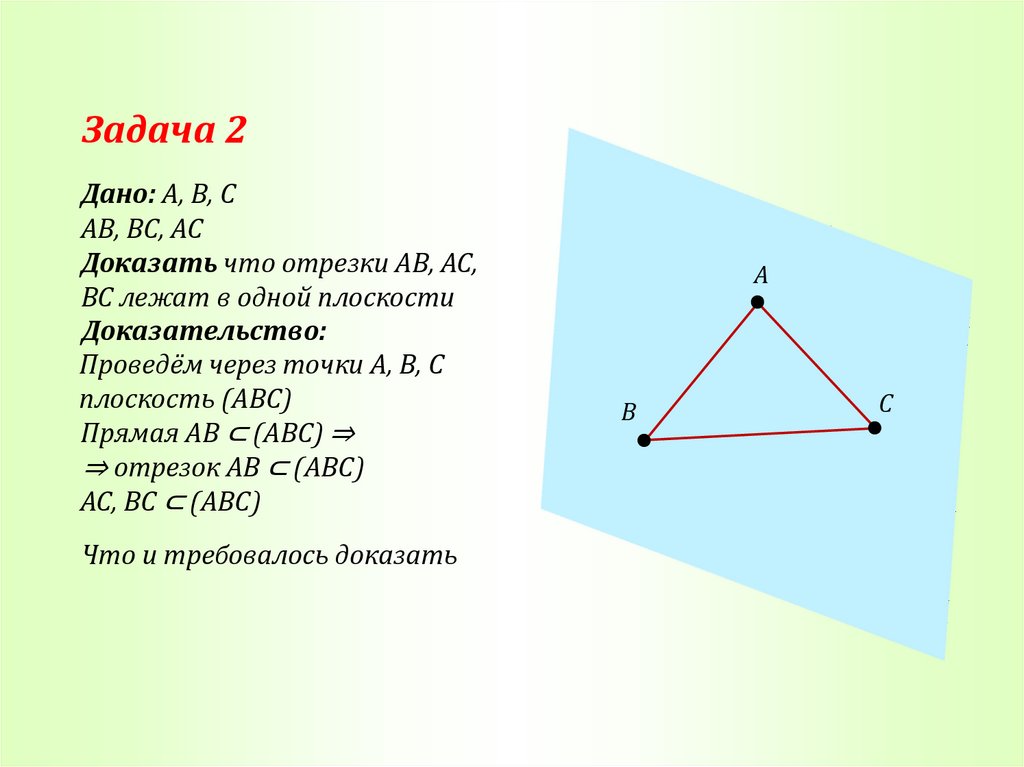
Задача 2
Дано: А, В, С
АB, ВC, AС
Доказать что отрезки АВ, АС,
ВС лежат в одной плоскости
Доказательство:
Проведём через точки А, В, С
плоскость (ABC)
Прямая AB ⊂ (ABC) ⇒
⇒ отрезок AB ⊂ (ABС)
АС, ВС ⊂ (АВС)
Что и требовалось доказать
A
B
C

18. Определите: верно, ли суждение?

В стереометрии мы будем рассматривать ситуации, задающие различные
расположения в пространстве основных фигур относительно друг друга
Определите: верно, ли суждение?
1.
2.
3.
4.
5.
6.
7.
8.
ДА
Любые три точки лежат в одной плоскости.
НЕТ
Любые четыре точки лежат в одной плоскости.
Любые четыре точки не лежат в одной плоскости.
НЕТ
Через любые три точки проходит плоскость и при том
НЕТ
только одна.
Если прямая пересекает 2 стороны треугольника, то
ДА
она лежит в плоскости треугольника.
Если прямая проходит через вершину треугольника, то НЕТ
она лежит в плоскости треугольника.
НЕТ
Если прямые не пересекаются, то они параллельны.
Если плоскости не пересекаются, то они параллельны. ДА

19. Аксиомы стереометрии

Слово «аксиома» греческого происхождения и в переводе означает
истинное, исходное положение теории.
Определение
Аксиома – это утверждение не требующее
доказательства.
Аксиомы стереометрии – утверждения о свойствах геометрических
тел, принимаемые в качестве исходных положений, на основе которых
доказываются все теоремы и вообще строится вся геометрия.
Система аксиом стереометрии дает описание
свойств пространства и основных его элементов
Понятия «точка», «прямая», «плоскость», «расстояние»
принимаются без определений: их описание и свойства содержатся в
аксиомах

20. Аксиомы стереометрии

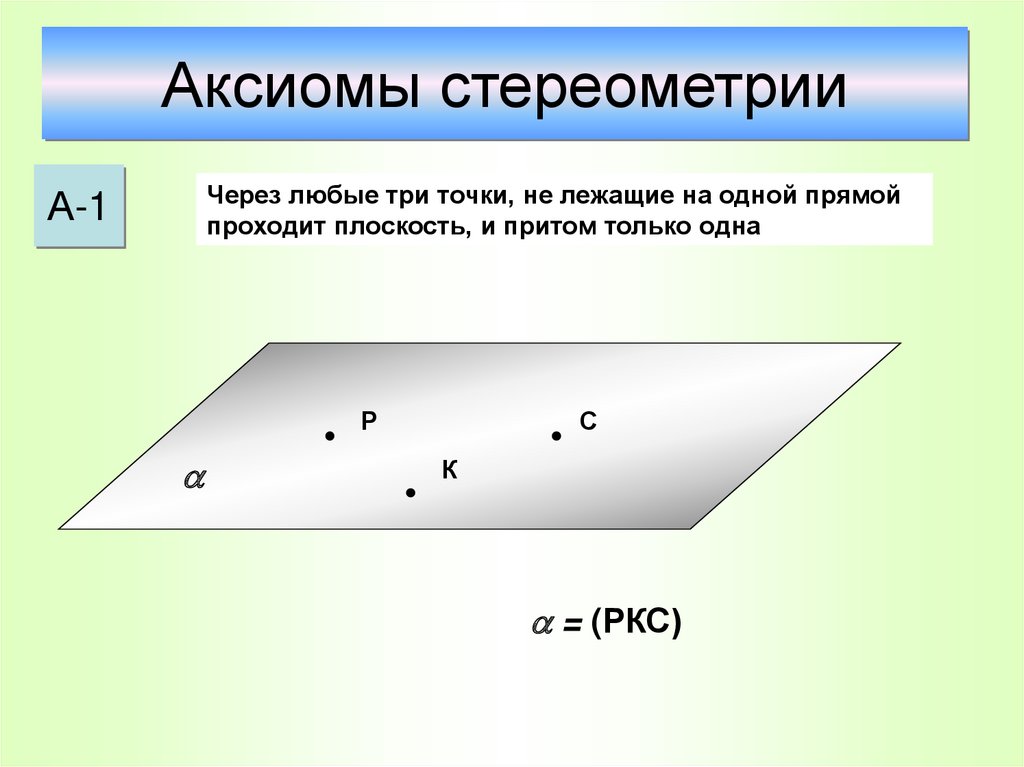
Через любые три точки, не лежащие на одной прямой
проходит плоскость, и притом только одна
А-1
Р
С
К
= (РКС)

21. Аксиомы стереометрии

А-2
Если две точки прямой лежат в плоскости, то все точки
прямой лежат в этой плоскости.
Если
М, C
М, C m,
то
m

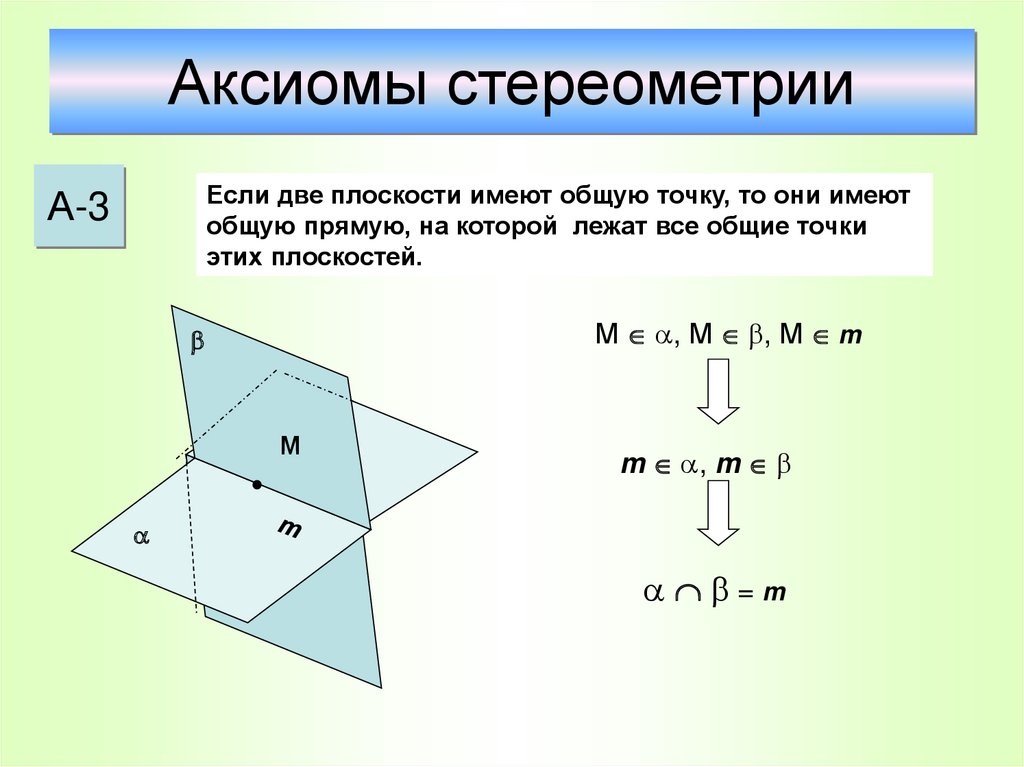
22. Аксиомы стереометрии

Если две плоскости имеют общую точку, то они имеют
общую прямую, на которой лежат все общие точки
этих плоскостей.
А-3
М , М , М m
М
m , m
=m

23. СЛЕДСТВИЯ ИЗ АКСИОМ

Через любую прямую и не принадлежащую ей точку
можно провести плоскость, и притом только одну.
Т-1
Дано: М m
В
А
м
Доказательство
Пусть точки A, B m.
Так как М m, то точки А, В и M не принадлежат одной прямой.
По А-1 через точки А, В и M проходит только одна плоскость — плоскость (ABM),
Обозначим её . Прямая m имеет с ней две общие точки — точки A и B, следовательно,
по аксиоме А-2 эта прямая лежит в плоскости ..
Таким образом, плоскость проходит через прямую m и точку M и является искомой.
Докажем, что другой плоскости, проходящей через прямую m и точку M, не существует.
Предположим, что есть другая плоскость — , проходящая через прямую m и точку M.
Тогда плоскости и проходят через точки А, В и M, не принадлежащие одной прямой, а
значит, совпадают. Следовательно, плоскость единственна.
Теорема доказана

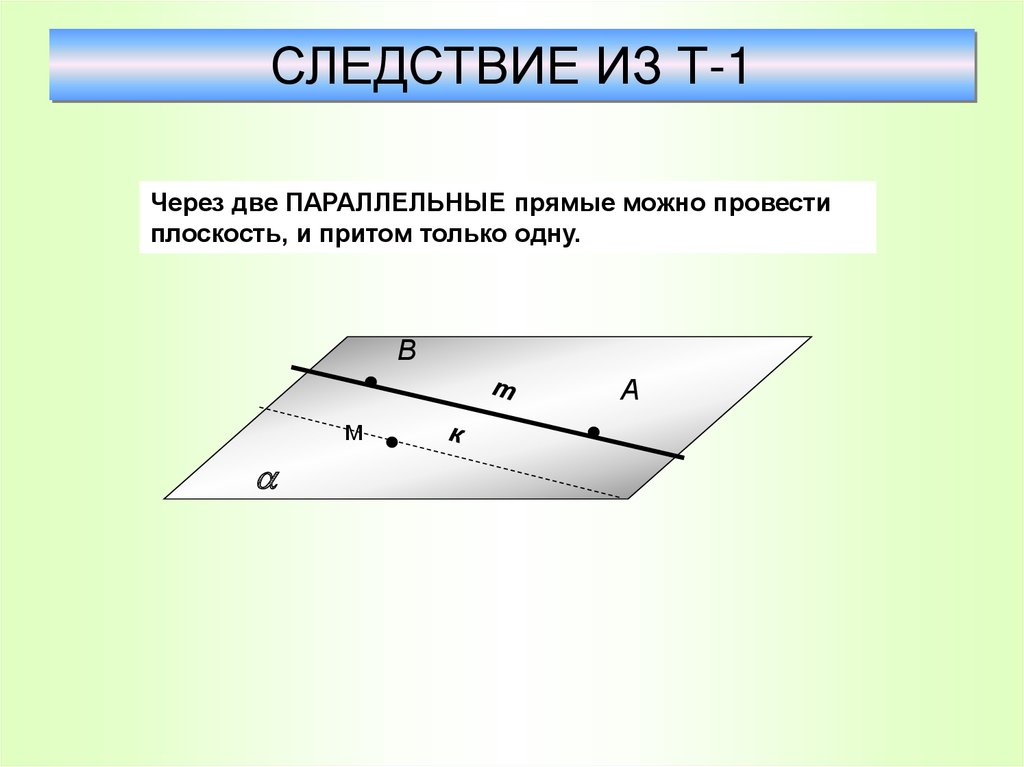
24. СЛЕДСТВИЕ ИЗ Т-1

Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести
плоскость, и притом только одну.
В
А
м

25. СЛЕДСТВИЯ ИЗ АКСИОМ

Через любые две пересекающиеся прямые можно
провести плоскость, и притом только одну.
Т-2
n
м
N
Дано: m n = M
Доказательство
Отметим на прямой m произвольную точку N,
отличную от М.
Рассмотрим плоскость =(n, N). Так как M и N , то по А-2 m . Значит
обе прямые m, n лежат в плоскости и следовательно , является искомой
Докажем единственность плоскости . Допустим, что есть другая, отличная от
плоскости и проходящая через прямые m и n, плоскость .
Так как плоскость проходит через прямую n и не принадлежащую ей точку N, то по
T-1 она совпадает с плоскостью . Единственность плоскости доказана.
Теорема доказана

26. ВЫВОД

Как в пространстве можно однозначно задать плоскость?
По трем точкам, не лежащим на одной прямой
По прямой и точке, не лежащей на этой прямой
По двум пересекающимся прямым
По двум параллельным прямым

27.

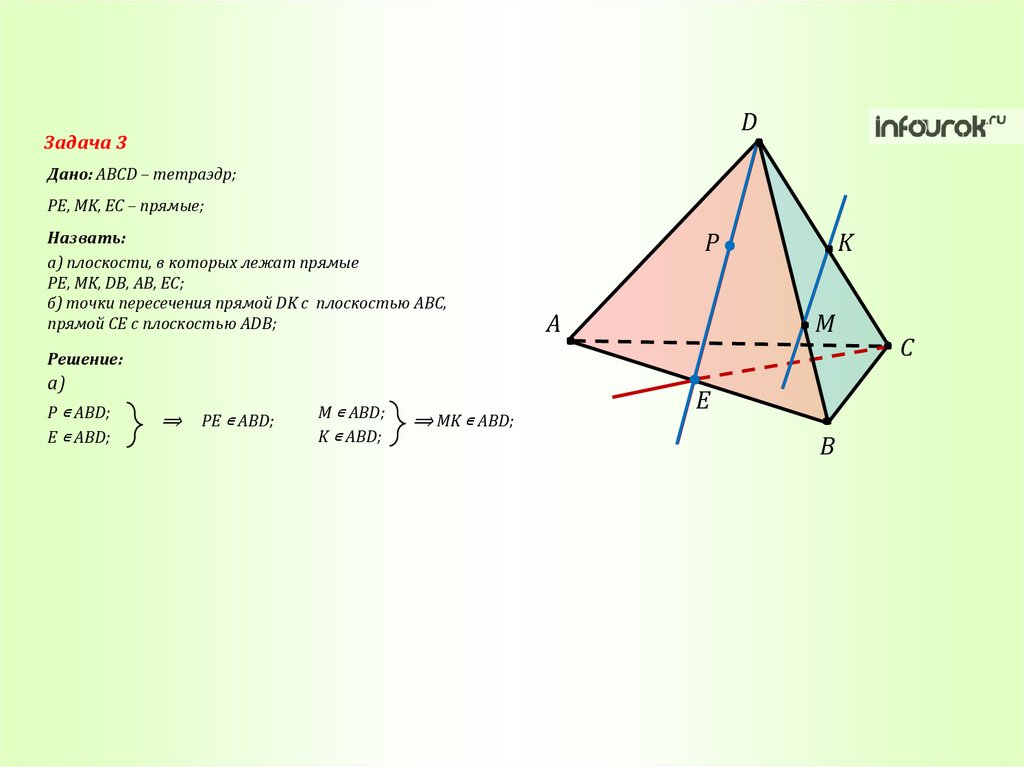
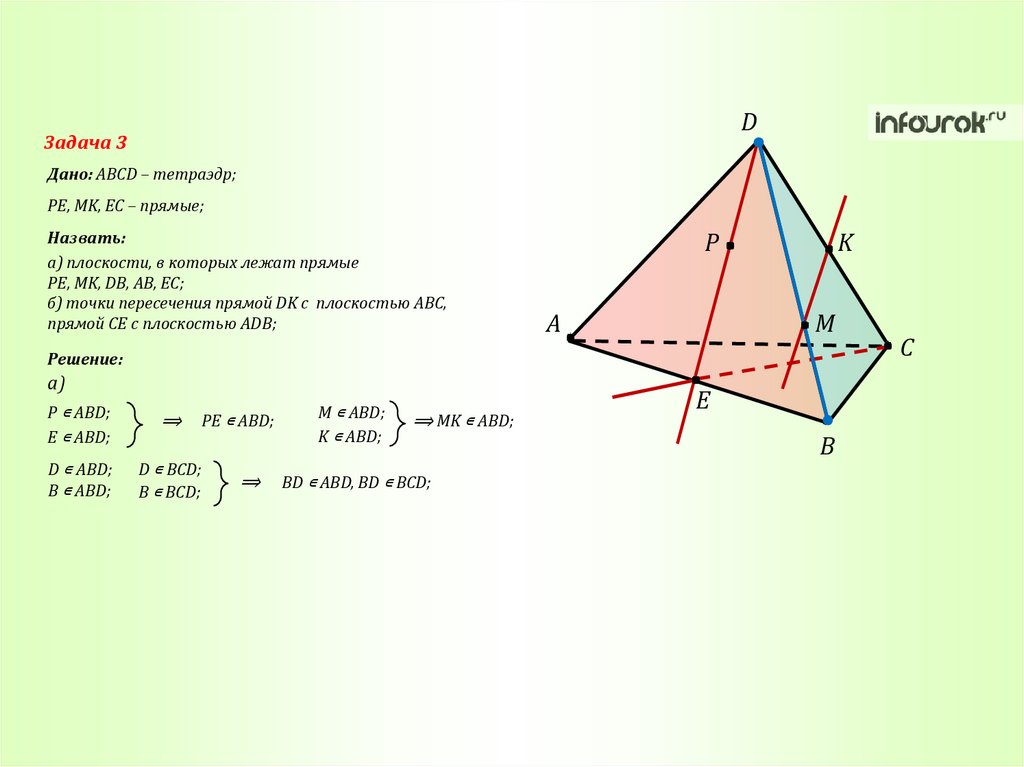
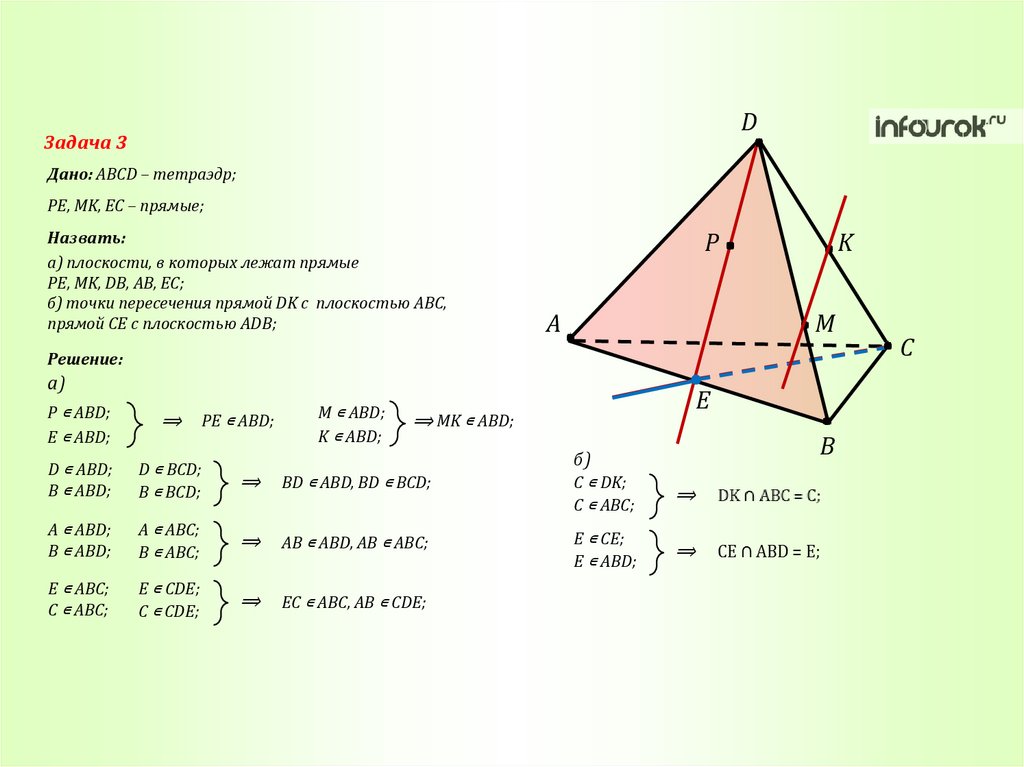
D
Задача 3
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
P ∊ ABD;
E ∊ ABD;
⟹
PE ∊ ABD;
M ∊ ABD;
K ∊ ABD;
⟹ MK ∊ ABD;
E
B
C

28.

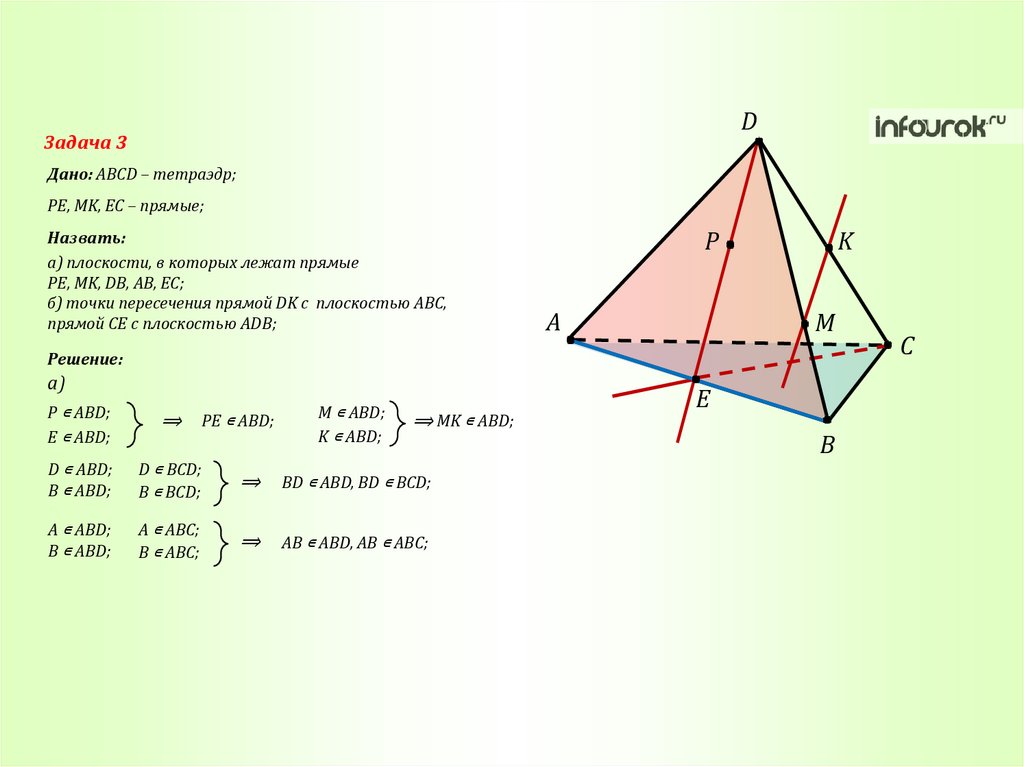
D
Задача 3
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
PE ∊ ABD;
⟹
M ∊ ABD;
K ∊ ABD;
⟹ MK ∊ ABD;
BD ∊ ABD, BD ∊ BCD;
E
B
C

29.

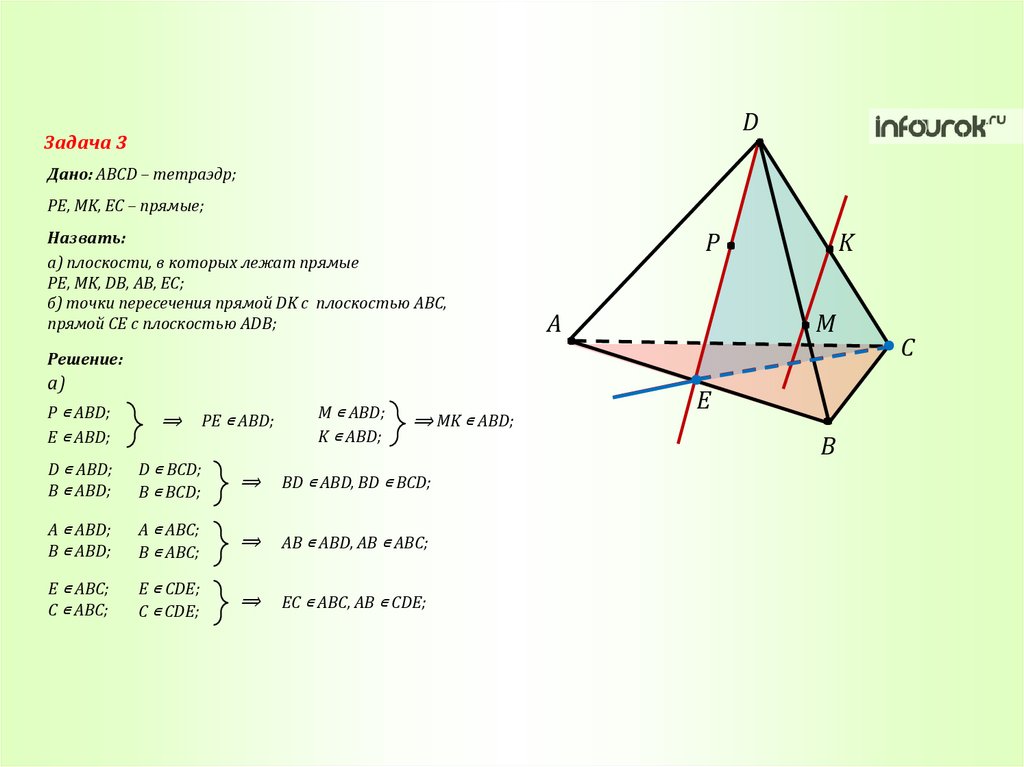
D
Задача 3
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
M ∊ ABD;
K ∊ ABD;
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
⟹
BD ∊ ABD, BD ∊ BCD;
A ∊ ABD;
B ∊ ABD;
A ∊ ABC;
B ∊ ABC;
⟹
AB ∊ ABD, AB ∊ ABC;
PE ∊ ABD;
⟹ MK ∊ ABD;
E
B
C

30.

D
Задача 3
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
M ∊ ABD;
K ∊ ABD;
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
⟹
BD ∊ ABD, BD ∊ BCD;
A ∊ ABD;
B ∊ ABD;
A ∊ ABC;
B ∊ ABC;
⟹
AB ∊ ABD, AB ∊ ABC;
E ∊ ABC;
C ∊ ABC;
E ∊ CDE;
C ∊ CDE;
⟹
EC ∊ ABC, AB ∊ CDE;
PE ∊ ABD;
⟹ MK ∊ ABD;
E
B
C

31.

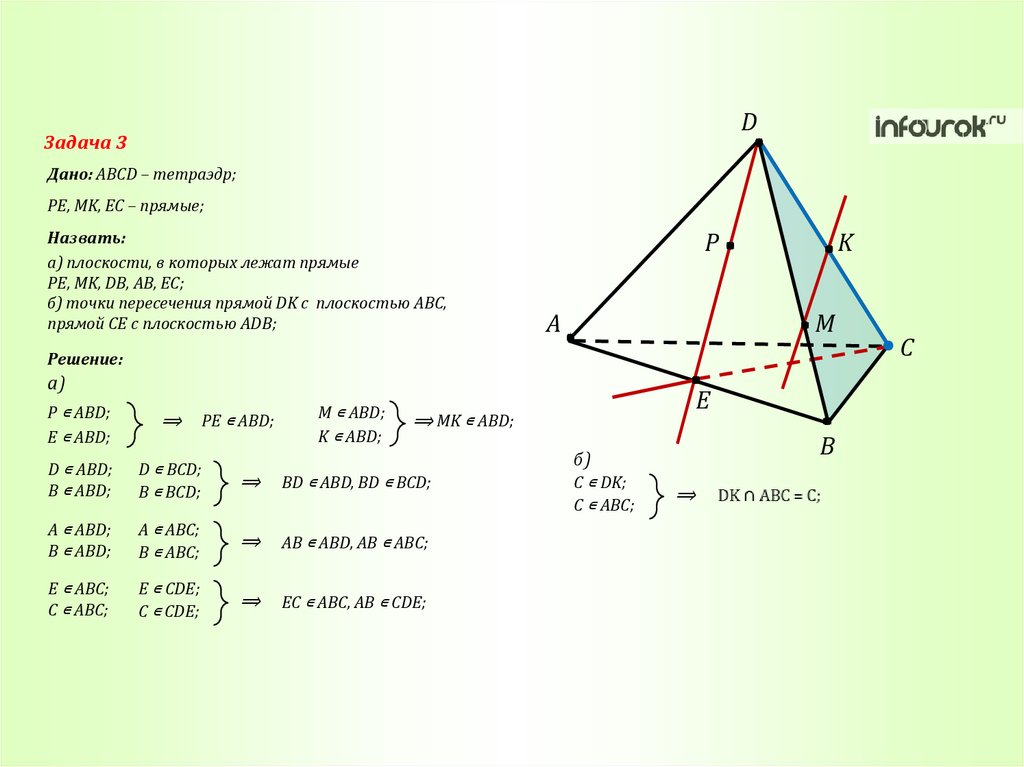
D
Задача 3
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
M ∊ ABD;
K ∊ ABD;
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
⟹
BD ∊ ABD, BD ∊ BCD;
A ∊ ABD;
B ∊ ABD;
A ∊ ABC;
B ∊ ABC;
⟹
AB ∊ ABD, AB ∊ ABC;
E ∊ ABC;
C ∊ ABC;
E ∊ CDE;
C ∊ CDE;
⟹
EC ∊ ABC, AB ∊ CDE;
PE ∊ ABD;
E
⟹ MK ∊ ABD;
B
б)
С ∊ DK;
C ∊ ABC;
⟹
C

32.

D
Задача 3
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
M ∊ ABD;
K ∊ ABD;
E
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
⟹
BD ∊ ABD, BD ∊ BCD;
С ∊ DK;
C ∊ ABC;
⟹
A ∊ ABD;
B ∊ ABD;
A ∊ ABC;
B ∊ ABC;
⟹
AB ∊ ABD, AB ∊ ABC;
E ∊ CE;
E ∊ ABD;
⟹
E ∊ ABC;
C ∊ ABC;
E ∊ CDE;
C ∊ CDE;
⟹
EC ∊ ABC, AB ∊ CDE;
PE ∊ ABD;
⟹ MK ∊ ABD;
B
б)
C

33.

Задача 4
Дано:
A, B, C, D – не лежат в одной плоскости
D
C
Найти:
Могут ли 3 из них лежать на одной прямой?
B
Решение.
A
Пусть: (A, B, C) ∊ m;
D ∉ m;
∃α: (A,C,D) ∊ α
(аксиома A1)
A∊α
(аксиома A2)
C∊α
⟹ B∊α
(A,B,C,D) ∊ α;
Ответ: Нет.
m

34.

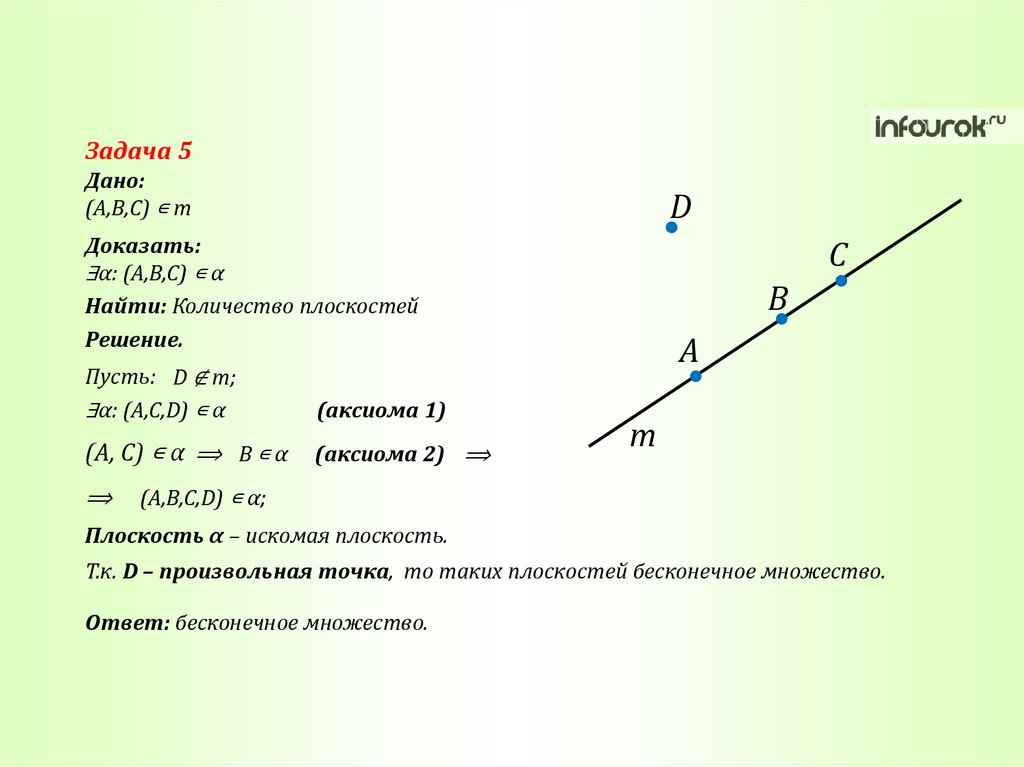
Задача 5
Дано:
(A,B,C) ∊ m
D
Доказать:
∃α: (A,B,С) ∊ α
Найти: Количество плоскостей
Решение.
Пусть: D ∉ m;
∃α: (A,C,D) ∊ α
(аксиома 1)
(A, C) ∊ α ⟹ B ∊ α
(аксиома 2) ⟹
⟹
C
B
A
m
(A,B,C,D) ∊ α;
Плоскость α – искомая плоскость.
Т.к. D – произвольная точка, то таких плоскостей бесконечное множество.
Ответ: бесконечное множество.