Признак перпендикулярности прямой и плоскости (10 класс)

1.

ПРИЗНАК
ПЕРПЕНДИКУЛЯРНОСТИ
ПРЯМОЙ И ПЛОСКОСТИ
Урок геометрии в 10 классе
Подготовила учитель математики
филиала «Примокшанская СОШ»
МБОУ «Ковылкинская средняя
общеобразовательная школа имени
Героя Советского Союза
М.Г.Гуреева» Гусарова Т.Д.

2.

2-й урок по теме «Перпендикулярность
прямых и плоскостей».
Повторить:
-определение перпендикулярных прямых;
-лемма;
-определение прямой, перпендикулярной
к плоскости;
-теорема о параллельных прямых,
перпендикулярных к плоскости
(прямая и обратная)

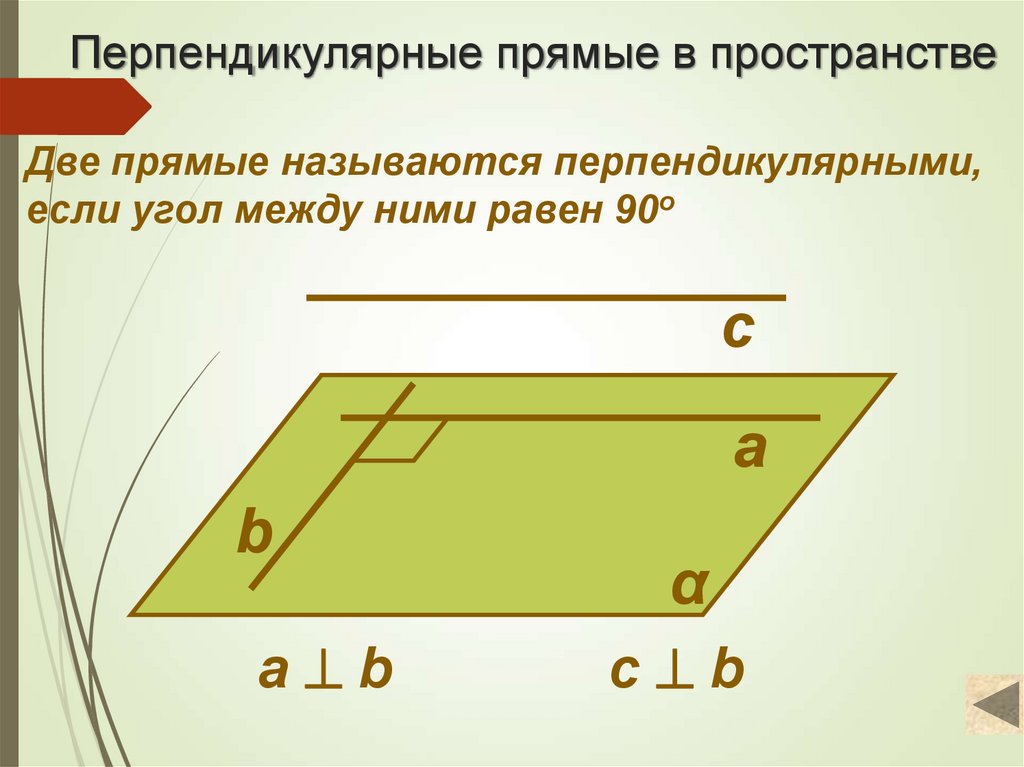
3. Перпендикулярные прямые в пространстве

Две прямые называются перпендикулярными,
если угол между ними равен 90о
с
а
b
а b
α
c b

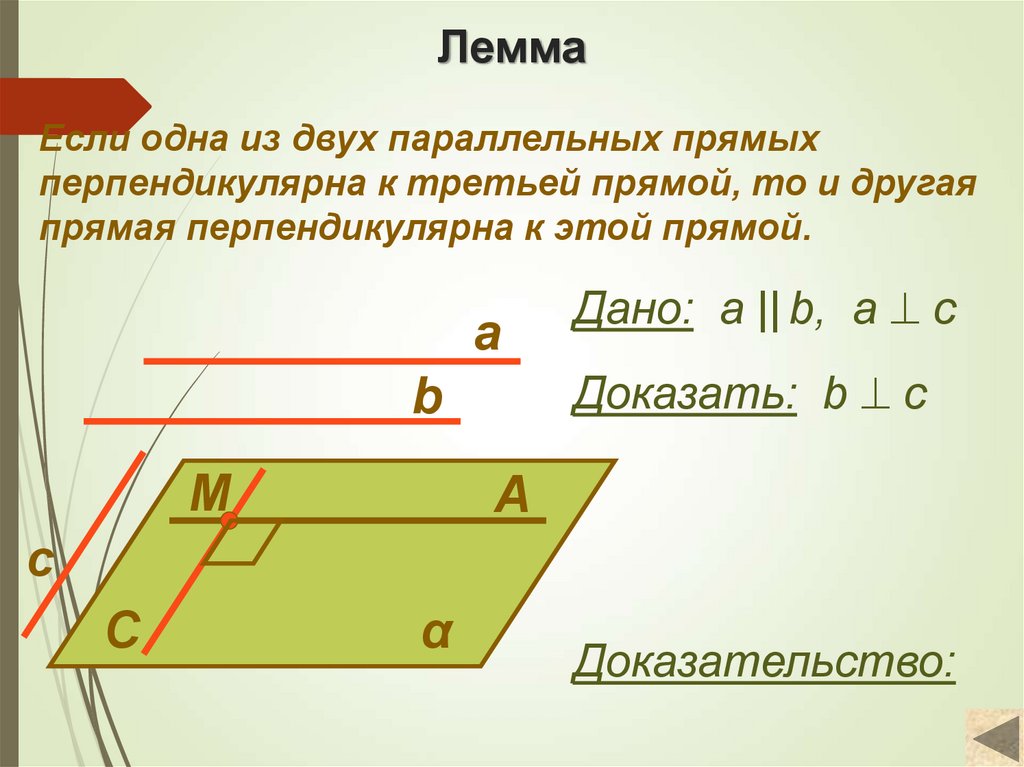
4. Лемма

Если одна из двух параллельных прямых
перпендикулярна к третьей прямой, то и другая
прямая перпендикулярна к этой прямой.
a
Доказать: b c
b
M
Дано: а || b, a c
A
c
C
α
Доказательство:

5. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости

а
α
а α

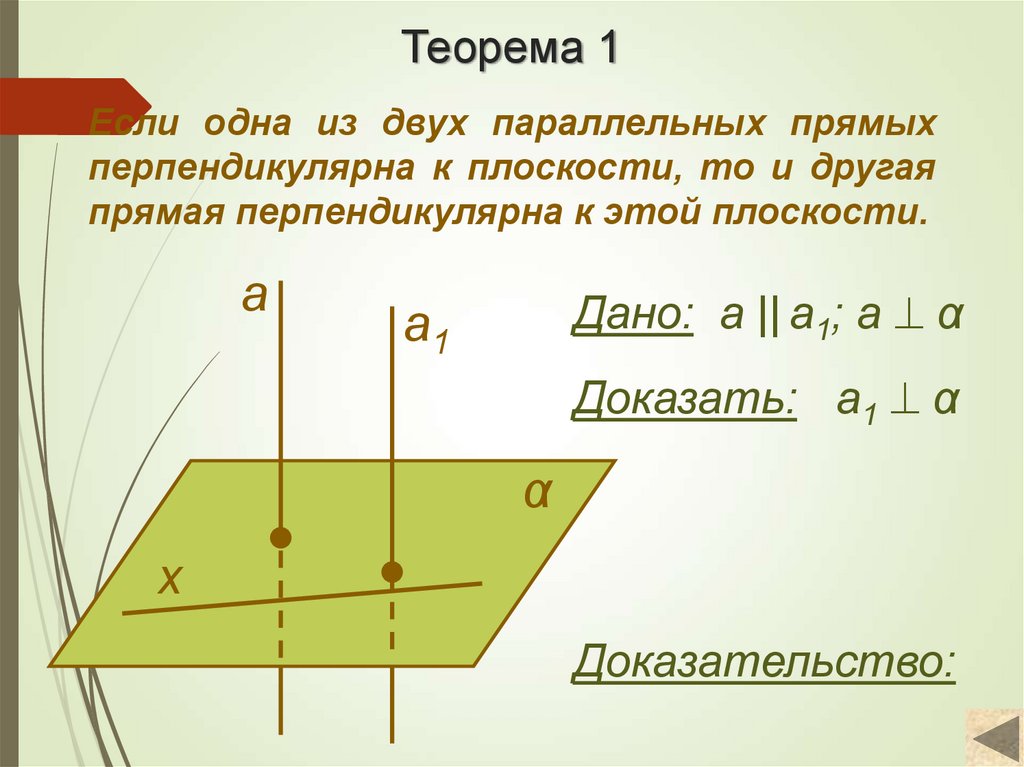
6. Теорема 1

Если одна из двух параллельных прямых
перпендикулярна к плоскости, то и другая
прямая перпендикулярна к этой плоскости.
a
Дано: а || а1; a α
а1
Доказать: а1 α
α
х
Доказательство:

7. Теорема 2

β
Если две прямые
перпендикулярны к
плоскости, то они
параллельны.
M
с
Дано: а α; b α
α
a
b
b1
Доказать: а || b
Доказательство:

8.

Устная работа
A
O
b
α
D
1. Дано: ОА ┴ α.
Найдите АОС, АОВ, AOD.
Найдите (а, b).
B
C
a
M
A
H
C
2. Дано: АМ ┴ (АВС), ВН – медиана
B Δ АВС
Найдите (ВН, АМ).

9.

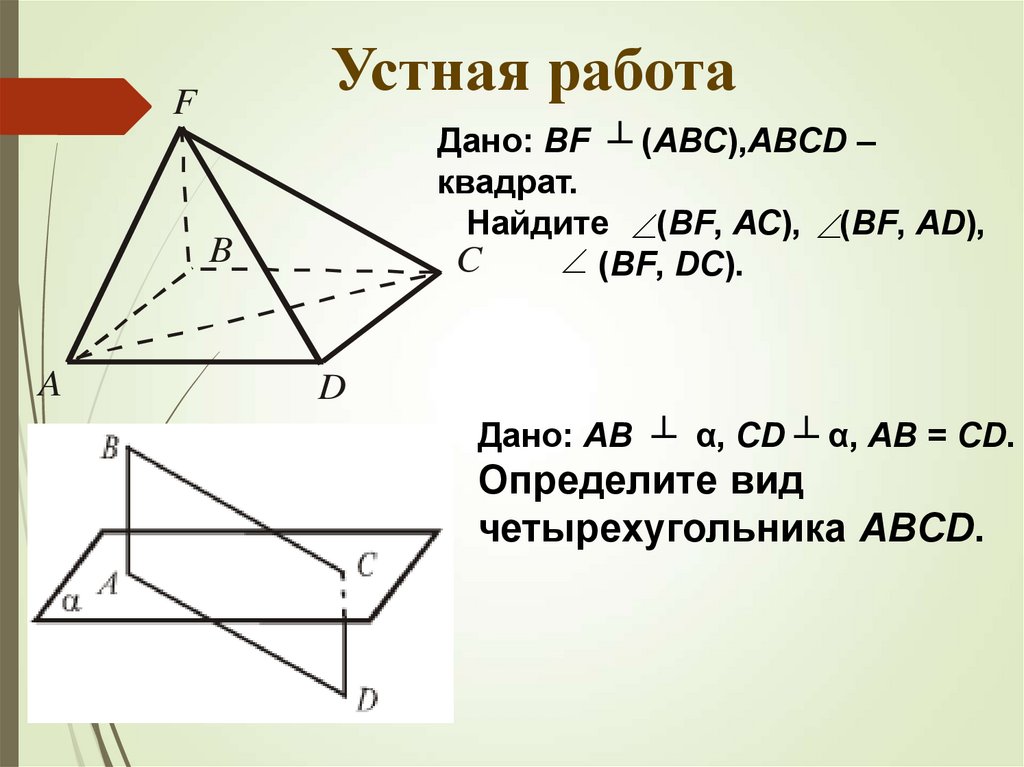
Устная работа
F
Дано: BF ┴ (АВС),ABCD –
квадрат.
Найдите (BF, АС), (BF, AD),
C
(BF, DC).
B
A
D
Дано: АВ ┴ α, CD ┴ α, AB = CD.
Определите вид
четырехугольника ABCD.

10.

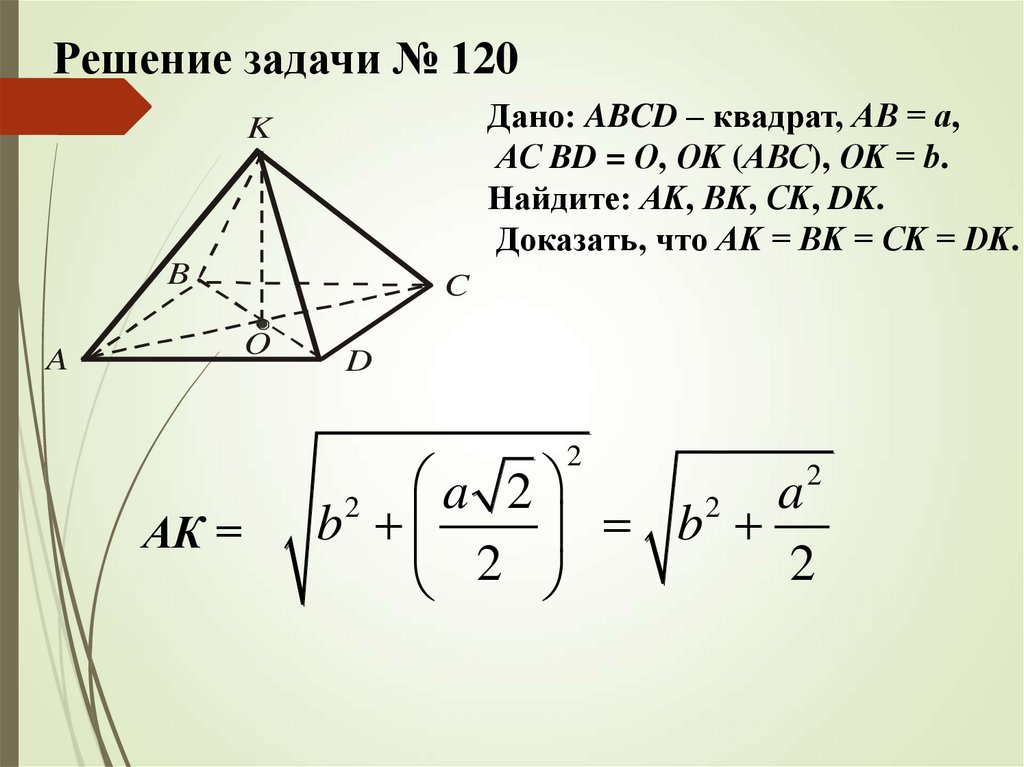
Решение задачи № 120
Дано: ABCD – квадрат, АВ = а,
АС BD = О, ОK (АВС), ОK = b.
Найдите: АK, ВK, СK, DK.
Доказать, что АK = ВK = СK = DK.
K
B
C
O
A
D
2
АК =
2
a 2
a
2
2
b
b
2
2

11.

ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ
ПРЯМОЙ И ПЛОСКОСТИ
Если прямая перпендикулярна к
двум пересекающимся прямым,
лежащим в плоскости, то она
перпендикулярна к этой плоскости

12.

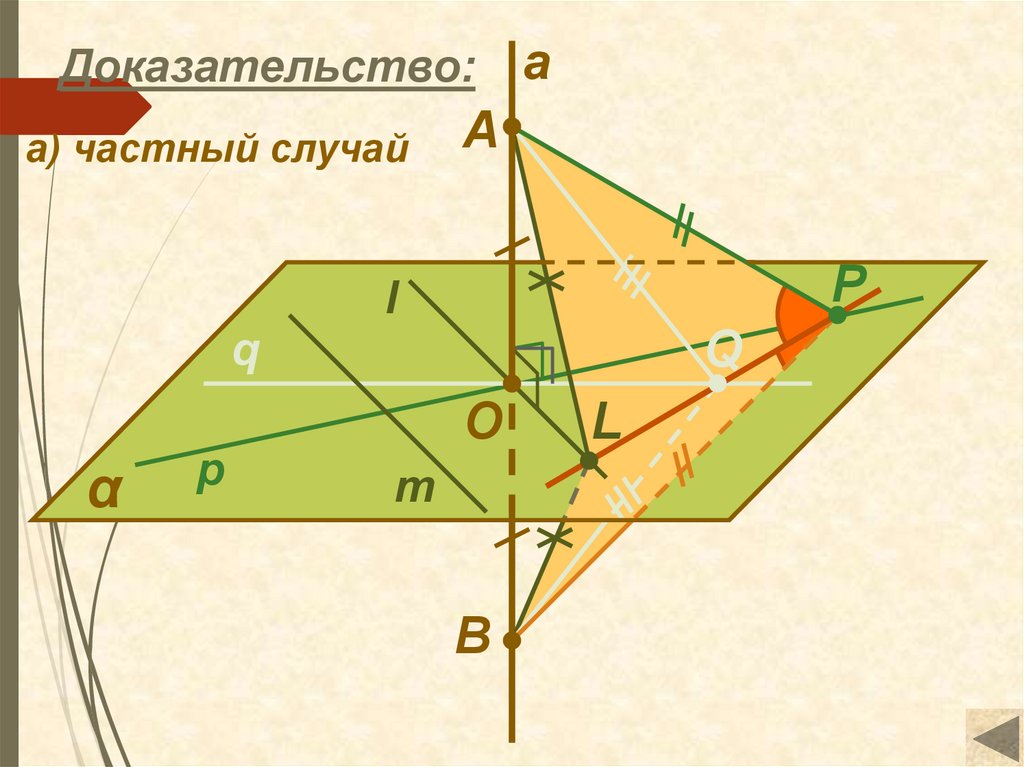
Доказательство:
а) частный случай
a
A
P
l
Q
q
O
α
p
m
B
L

13.

Доказательство:
а) общий случай
a1
a
m
q
p
O
α

14.

Решение задачи № 1
D
K
Дано: Δ ABC – правильный, CD ┴(АВС),
О – центр Δ АВС, ОK || CD,
АВ = 16 √3 см, ОK = 12 см, CD = 16 см.
Найдите: BD, AD, АK, ВK.
A
C
N
O
M
B

15.

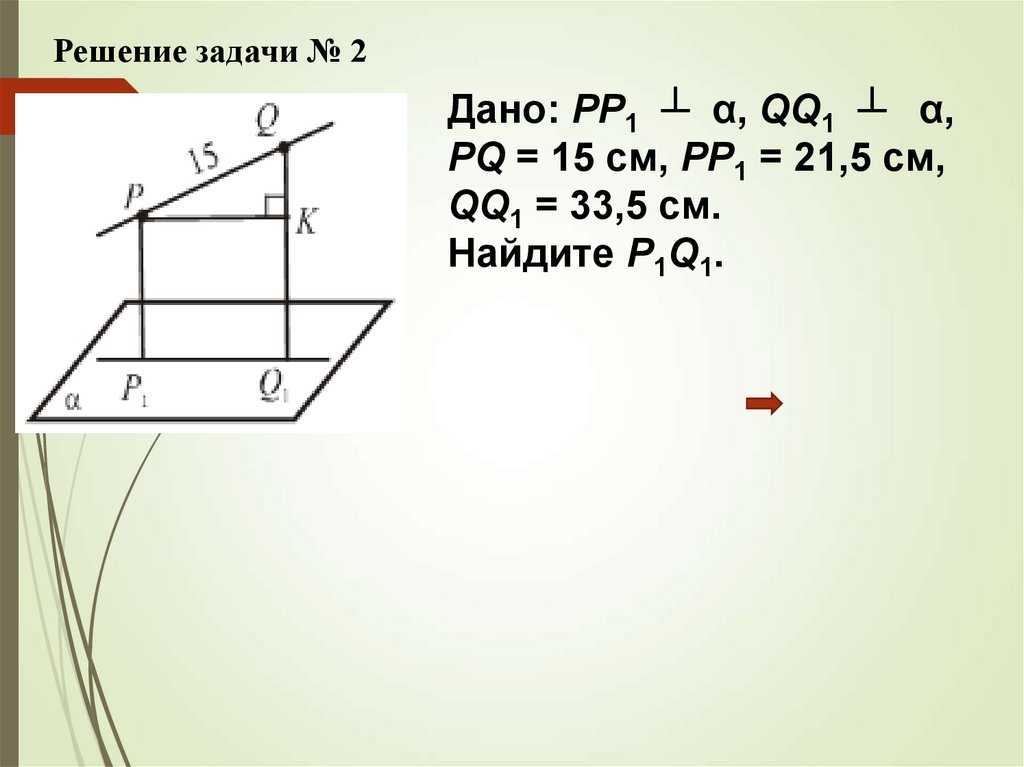
Решение задачи № 2
Дано: РР1 ┴ α, QQ1 ┴ α,
PQ = 15 см, РР1 = 21,5 см,
QQ1 = 33,5 см.
Найдите P1Q1.

16.

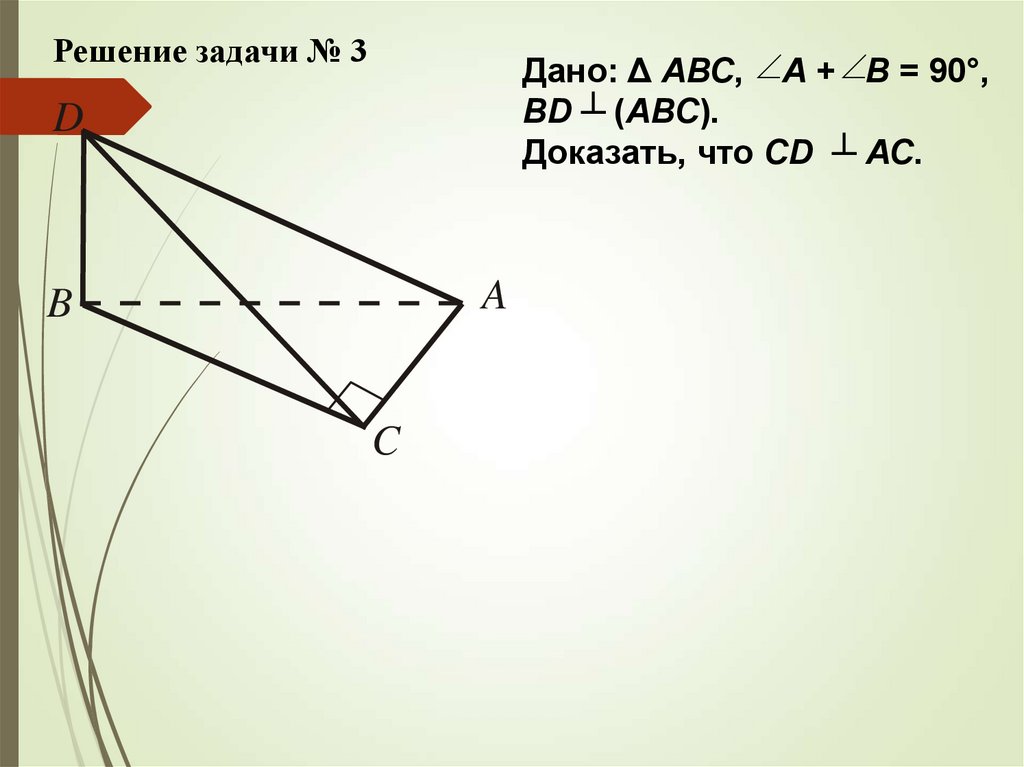
Решение задачи № 3
Дано: Δ АВС, А + В = 90°,
BD ┴ (АВС).
Доказать, что CD ┴ АС.
D
A
B
C

17.

Домашнее задание:
п. 9, выучить определения, теоремы.
№№ 9.11, 9.13 выполнить в тетради.