Основные понятия, теоремы, формулы вписанной и описанной окружности

1.

Вписанная и описанная
окружности
Основные понятия, теоремы, формулы

2.

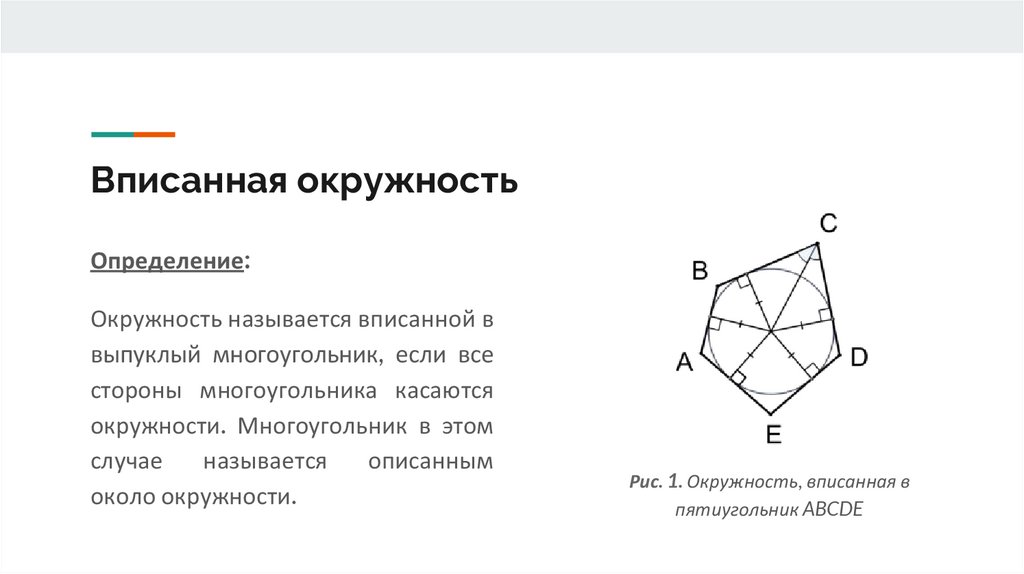
Вписанная окружность
Определение:
Окружность называется вписанной в
выпуклый многоугольник, если все
стороны многоугольника касаются
окружности. Многоугольник в этом
случае
называется
описанным
около окружности.
Рис. 1. Окружность, вписанная в
пятиугольник ABCDE

3.

Теорема об окружности, вписанной в
треугольник
Теорема: В любой треугольник
можно вписать окружность.
Рис. 2

4.

Теорема об окружности, вписанной в
треугольник
Доказательство: Рассмотрим произвольный
треугольник ABC и обозначим буквой O точку
пересечения его биссектрис. Точка O
равноудалена от всех сторон треугольника, т.е
OK=OL=OM. где OK, OL и OM –
перпендикуляры из точки O к сторонам AB, BC
и AC соответственно. Значит, O – центр
окружности, а AB, BC, AC – касательные к ней.
Таким образом, окружность вписана в
треугольник ABC.
Рис. 2

5.

Теорема об окружности, вписанной в
треугольник
Замечание 1: В треугольник можно вписать только одну окружность.
В самом деле, предположим, что в треугольник можно вписать две окружности. Тогда
центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с
точкой O пересечения биссектрис треугольника, а радиус равен расстоянию от точки
O до сторон треугольника. Следовательно, эти окружности совпадают.

6.

Теорема об окружности, вписанной в
треугольник
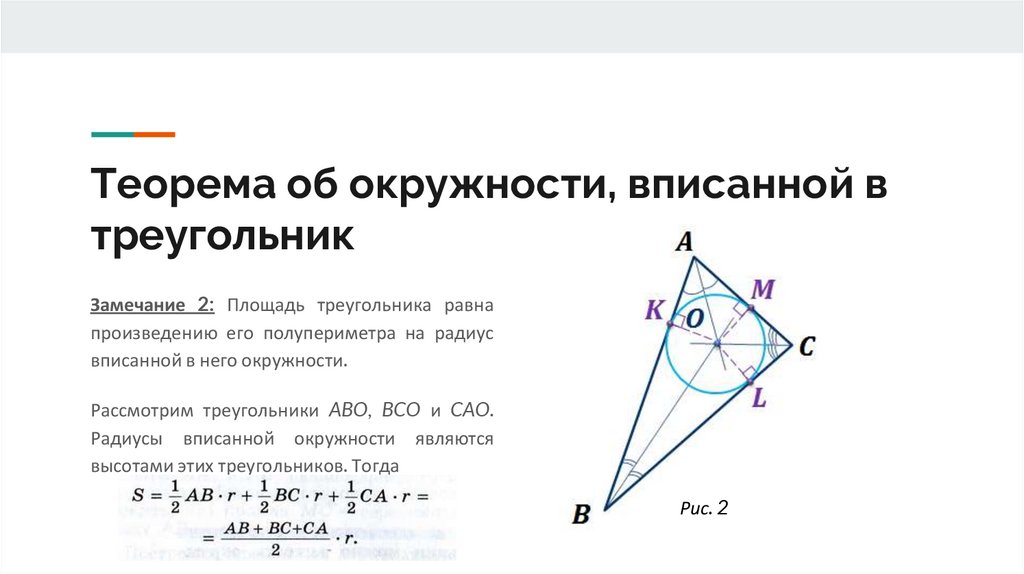
Замечание 2: Площадь треугольника равна
произведению его полупериметра на радиус
вписанной в него окружности.
Рассмотрим треугольники ABO, BCO и CAO.
Радиусы вписанной окружности являются
высотами этих треугольников. Тогда
Рис. 2

7.

Окружность, вписанная в четырехугольник
В четырехугольник не всегда можно вписать
окружность.
1. Если в четырехугольник можно вписать
окружность,
то
суммы
его
противоположных сторон равны.
На рис. 3 одними и теми же буквами
обозначены равные отрезки касательных. В
самом
деле
AB
+
CD
=x+y+u+z,
BC
+
AD
=x+y+u+z,
поэтому AB + CD=BC + AD.
Рис. 3

8.

Окружность, вписанная в четырехугольник
2. Если суммы противоположных
сторон выпуклого четырехугольника
равны, то в него можно вписать
окружность.
Рис. 3

9.

Описанная окружность
Определение:
Окружность называется описанной
около многоугольника, если все
вершины многоугольника лежат на
окружности.
Рис. 4. Окружность, описанная
около восьмиугольника

10.

Теорема об окружности, описанной
около треугольника
Теорема:
Около
любого
треугольника можно описать
окружность.
Рис. 5

11.

Теорема об окружности, описанной
около треугольника
Доказательство:
Рассмотрим
произвольный
треугольник ABC. Обозначим буквой O точку
пересечения серединных перпендикуляров к его
сторонам и соединим ее с вершинами
треугольника. Так как точка O равноудалена от
вершин треугольника ABC, то OA=OB=OC.
Поэтому окружность с центром O проходит через
все три вершины треугольника и, значит, является
описанной около треугольника ABC.
Рис. 5

12.

Теорема об окружности, описанной
около треугольника
Замечание 1: Около треугольника можно описать
только одну окружность.
В самом деле, допустим, что около треугольниа
можно описать две окружности. Тогда центр
каждой из них равноудален от его вершин и
поэтому совпадает с точкой O пересечения
серединных перпендикуляров к сторонам
треугольника, а радиус равен растоянию от точки
O до вершин треугольника. Следовательно, эти
окружности совпадают.
Рис. 5

13.

Окружность, описанная около
четырехугольника
Около четырехугольника не всегда можно описать окружность.
1.
В любом вписанном четырехугольнике сумма
противоположных углов равна 1800
По теореме о вписанном угле,
Рис. 6

14.

Окружность, описанная около
четырехугольника
2. Если сумма противоположных углов четырехугольника равна 1800, то
около него можно описать окружность.