Задача на нахождение средней скорости

1.

Если две точки одновременно начинают движение по окружности в одну сторону со скоростями
V₁ и V₂ , где V₁ > V₂ то первая точка приближается ко второй со скоростью V₁ - V₂ и в момент,
когда первая точка в первый раз догоняет вторую, она проходит расстояние на один круг
больше.
Задача №1
Из одной точки круговой трассы, длина которой равна 14 км, одновременно стартовали два
автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он
опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в
км/ч.
Решение
Пусть скорость второго автомобиля х км/ч. 40 минут это 2/3 часа и это – то время, за которое
первый автомобиль будет опережать второй на один круг, составим и решим уравнение:
14: (80-х)=2/3
х=59

2.

Задача на нахождение средней скорости.
Средняя скорость вычисляется по формуле V=S/t, где S - ВСЕ РАССТОЯНИЕ, ПРОЙДЕННОЕ
ТЕЛОМ, а t – ВСЕ ВРЕМЯ, ЗА КОТОРОЕ ЭТОТ ПУТЬ ПРОЙДЕН.
Задача №2
Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16
км/ч, а последнюю треть – 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении
всего пути. Ответ дайте в км/ч.
Решение
Обозначим длину трассы через 3 S. Тогда первую треть трассы велосипедист проехал за время
S/12, вторую треть за время S/16, а последнюю за S/24. значит, время, затраченное на весь путь
равно S/12 + S/16 + S/24= 9S/48. Скорость3S/9S/48=16 км/ч

3.

Задача на движение протяженных тел.
В задачах такого типа требуется, как правило, определить длину одного из этих тел. Наиболее
типичная ситуация: определение длины поезда, проезжающего мимо столба или протяженной
платформы. В первом случае поезд проходит мимо столба расстояние, равное длине поезда,
во втором случае-расстояние, равное сумме длин поезда и платформы.
Задача №3
Найти скорость и длину поезда, зная, что он проходит с постоянной скоростью мимо
неподвижного наблюдателя в течении 7 с и затратил 25 секунд на то, чтобы пройти с той же
скоростью вдоль платформы длиной 378 м.
Решение
Пусть длина поезда –у метров, а скорость поезда – х м/с. Тогда х=у/7. За 25 секунд поезд
пройдет расстояние равное (378+у) метров. Составим и решим уравнение:
25*у/7=у+378
У=147 метров
Длина поезда 147 метров. Скорость поезда = 147/7 м/с=75,6 км/ч

4.

Задача №4
По морю параллельными курсами в одном направлении следуют два
сухогруза: первый длиной 120 метров, второй-длиной 80 метров. Сначала
второй сухогруз отстает от первого и в некоторый момент времени
расстояние от кормы первого сухогруза до носа второго сухогруза составляет
400 м. через 12 минут после этого уже первый сухогруз отстает от второго так,
что расстояние от кормы второго сухогруза до носа первого равно 600 м. На
сколько км/ч скорость первого сухогруза меньше скорости второго?
Решение
За 12 минут второй сухогруз проходит расстояние равное 400+120+600+80
Поэтому скорость второго равна 1200/12=100 м/мин или 6 км/ч.

5.

Задачи на производительность.
В определенном смысле задачи на работу схожи с задачами на движение: роль скорости здесь играет
производительность труда, роль расстояния- объем работы. В тех случаях, когда объем работы не
задан, его удобно принять равным единице.
Существенно разных задач здесь практически нет, во всех случаях речь идет о выполнении
определенной работы, меняются только сюжеты, а математическая фабула остается одной и той же.
Иногда в задачах на работу выделяют группу задач на трубы и бассейны, решение которых, вообще
говоря, не имеет никаких специфических черт по сравнению с другими задачами на работу.
Задача №5
Каждый из двух рабочих одинаковый квалификации может выполнить заказ за 15 часов. Через 3 часа
после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и
работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение
всего заказа?
Решение
V
T
A
1 рабочий
1/15
15
1
2 рабочий
1/15
15
1
Вместе
2/15
1
Пусть х часов они работали вместе,
Тогда можно составить уравнение
3*1/15+х*2/15=1
Х=6 часов

6.

Задачи на проценты, концентрацию, части ,доли.
При решении задач на проценты важно четко понимать что процент- это просто сотая часть
числа.
Задача №6
Брюки дороже рубашки на 20% и дешевле пиджака на 46%. На сколько процентов рубашка
дешевле пиджака?
Решение
Брюки
Рубашка
120% - ? р
100%-х р
Брюки
Пиджак
1.2 * х р
?Р
54%
100%
120х/54 р стоит пиджак
Рубашка
Пиджак
хр
120х/54 р
?%
100%
(100х) : (120х/54)=45%
100-45=55%
х*1.2 р стоят брюки

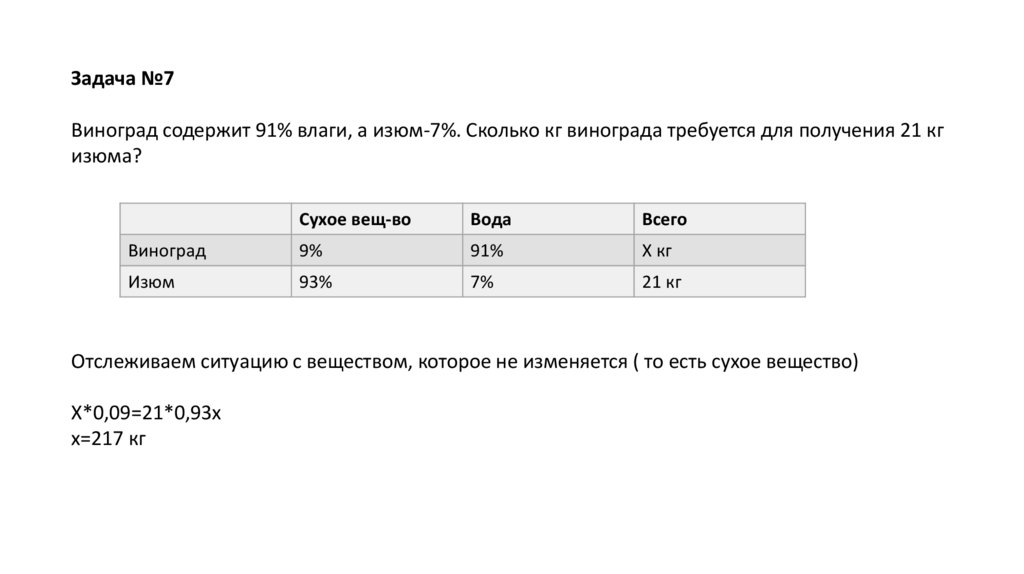
7.

Задача №7
Виноград содержит 91% влаги, а изюм-7%. Сколько кг винограда требуется для получения 21 кг
изюма?
Сухое вещ-во
Вода
Всего
Виноград
9%
91%
Х кг
Изюм
93%
7%
21 кг
Отслеживаем ситуацию с веществом, которое не изменяется ( то есть сухое вещество)
Х*0,09=21*0,93х
х=217 кг