Похожие презентации:
Функция. Прямая
1.
3.1.
Ф У Н К Ц И
2.
П Р Я М А Я
П А Р А
4.
5.
6.
Я
Б О Л А
В Е
Р Ш И Н А
О Р Д И Н А Т А
А Р Г У М Е Н Т
7.
К О Р
8. А
Е Н Ь
Б С Ц И С С А
9.
В Е
Т В Ь
9. Парабола состоит из двух частей,
3.График
1.
4.
8.
2.5.
y=kx+b,
Точка
6.
Первая
График
Вторая
7.
В X+5=0,
записи
(0,0)
квадратичной
координата
линейной
y=kx,
координата
–y=kx+b
x=-5,
для
y=x²
параболы
что
функции
-точки
xвсе
функции
точки
-такое
…?
это
-…
…?
--5?
-…
…?
….
-??… ?
каждая из которых называется - …?
2. Повторение
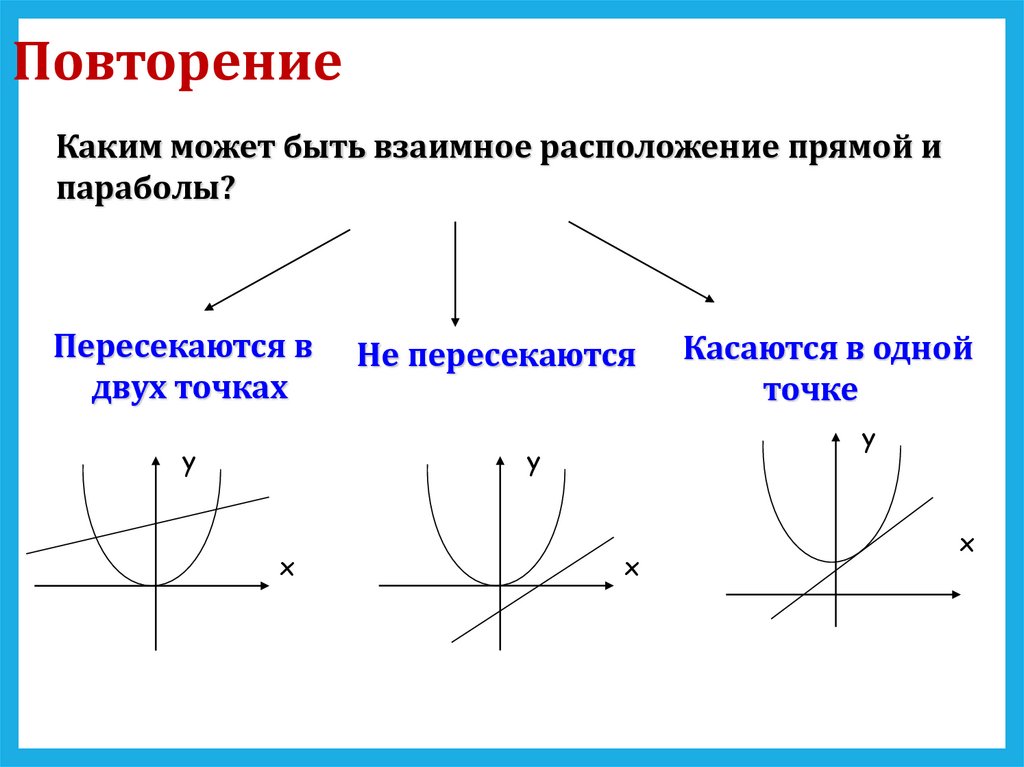
Каким может быть взаимное расположение прямой ипараболы?
Пересекаются в
двух точках
Не пересекаются
у
у
у
х
Касаются в одной
точке
х
х
3. Графический способ решения уравнений.
ГРАФИЧЕСКИЙСПОСОБ
РЕШЕНИЯ
УРАВНЕНИЙ.
4.
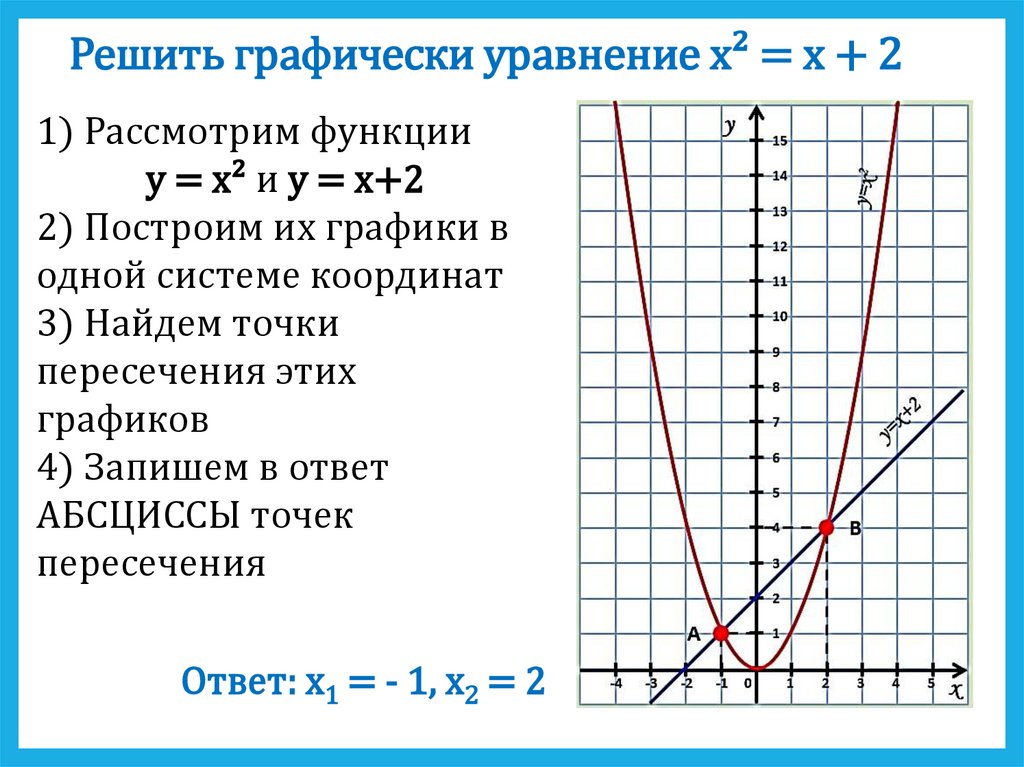
Решить графически уравнение x² = x + 21) Рассмотрим функции
y = x² и y = x+2
2) Построим их графики в
одной системе координат
3) Найдем точки
пересечения этих
графиков
4) Запишем в ответ
АБСЦИССЫ точек
пересечения
Ответ: х1 = - 1, х2 = 2
5.
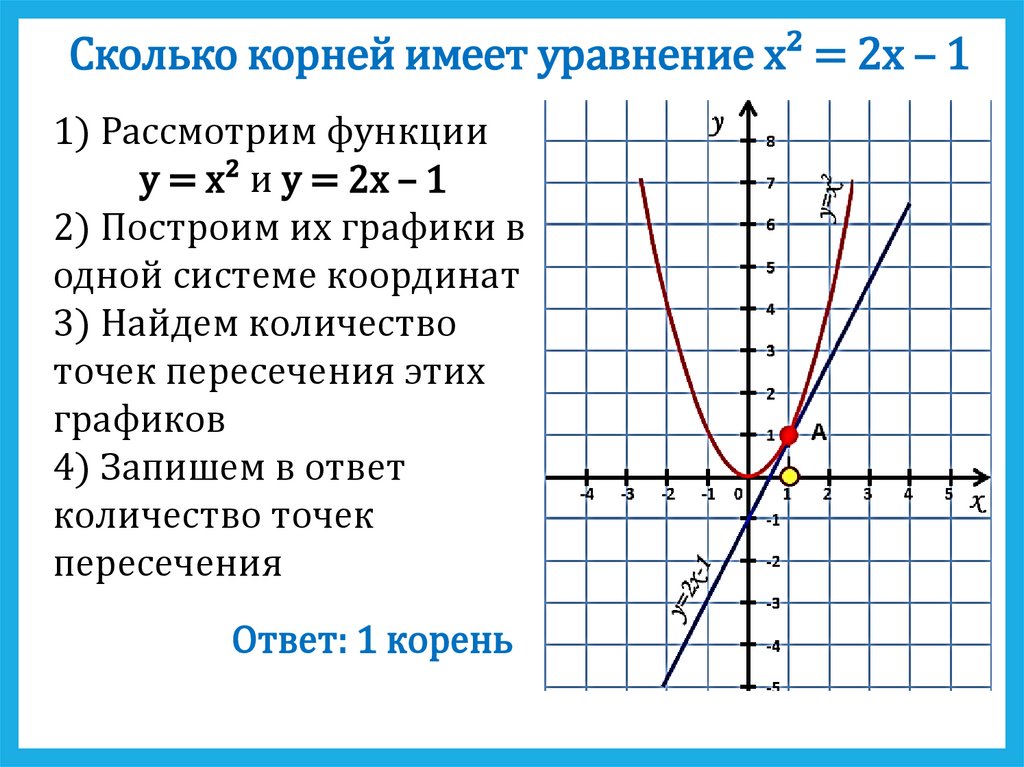
Сколько корней имеет уравнение x² = 2х – 11) Рассмотрим функции
y = x² и y = 2x – 1
2) Построим их графики в
одной системе координат
3) Найдем количество
точек пересечения этих
графиков
4) Запишем в ответ
количество точек
пересечения
Ответ: 1 корень
6.
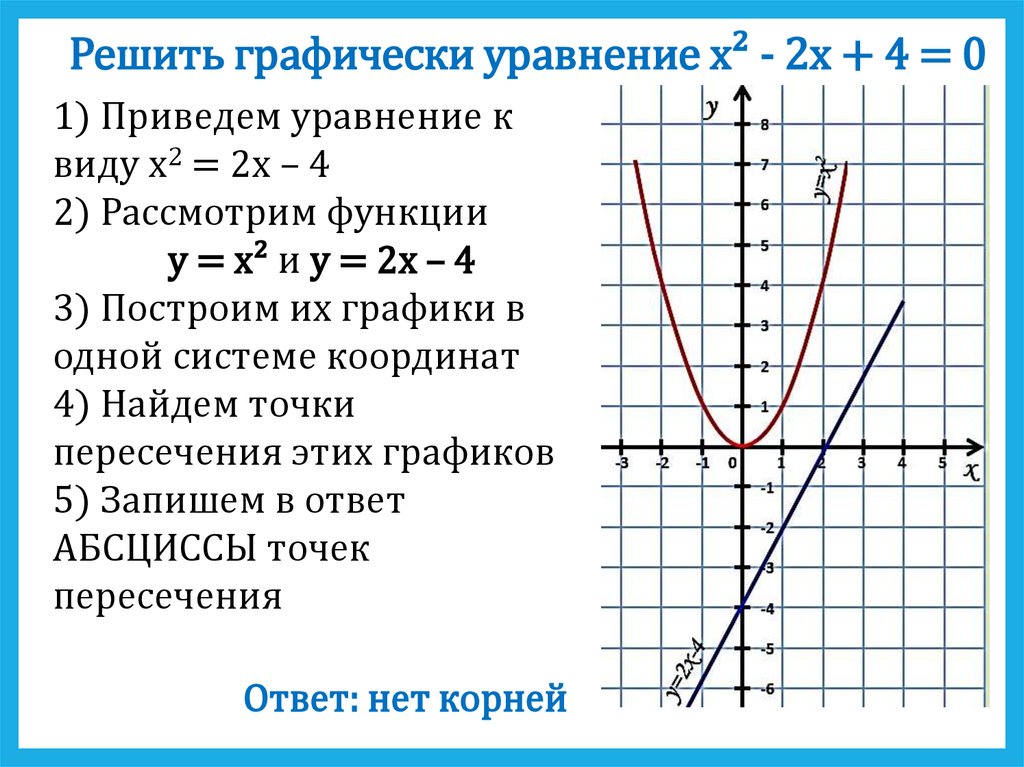
Решить графически уравнение x² - 2х + 4 = 01) Приведем уравнение к
виду х2 = 2х – 4
2) Рассмотрим функции
y = x² и y = 2х – 4
3) Построим их графики в
одной системе координат
4) Найдем точки
пересечения этих графиков
5) Запишем в ответ
АБСЦИССЫ точек
пересечения
Ответ: нет корней
7.
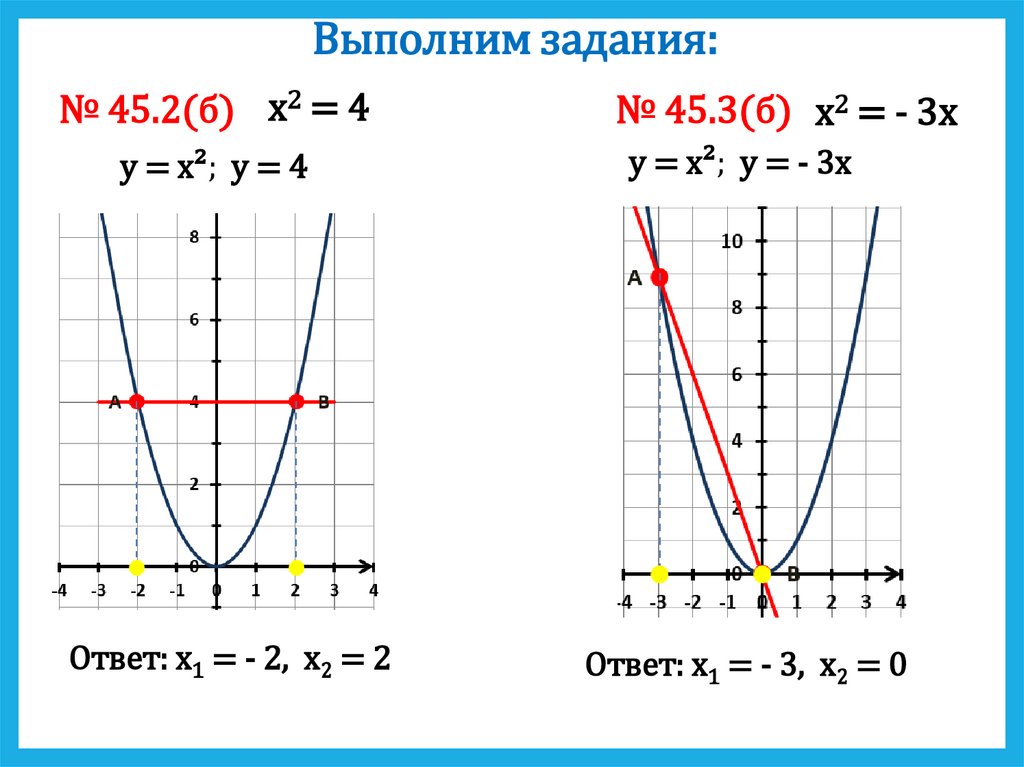
Выполним задания:№ 45.2(б) х2 = 4
y = x²; y = 4
Ответ: х1 = - 2, х2 = 2
№ 45.3(б) х2 = - 3х
y = x²; y = - 3х
Ответ: х1 = - 3, х2 = 0
8.
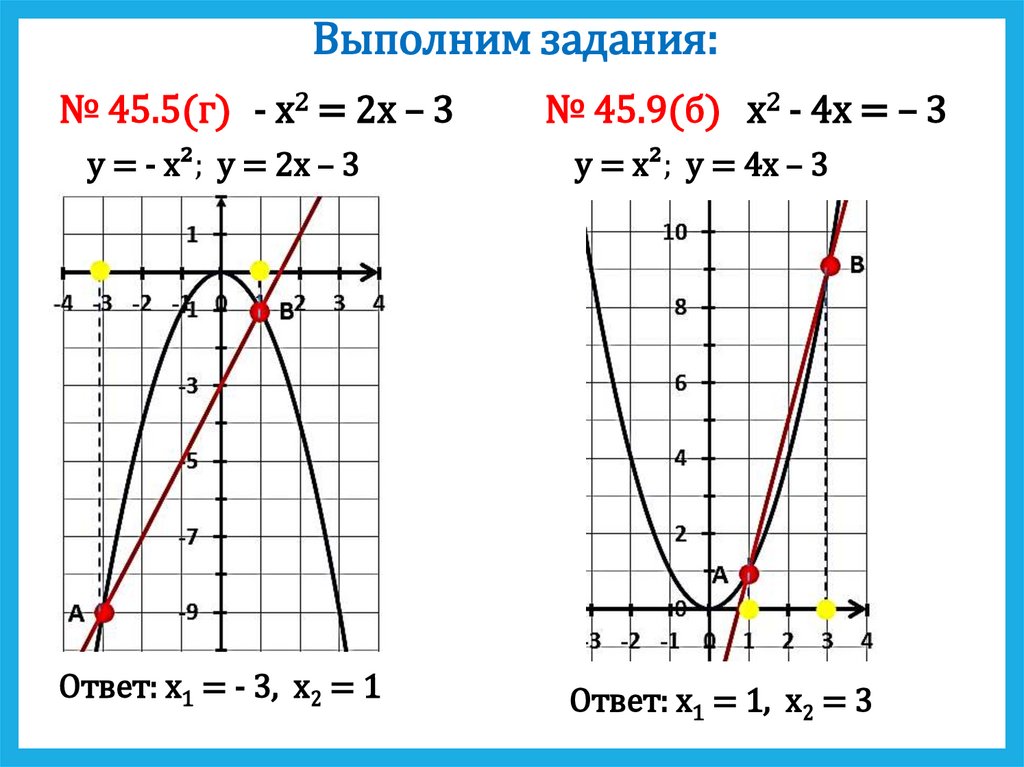
Выполним задания:№ 45.5(г) - х2 = 2х – 3
y = - x²; y = 2х – 3
Ответ: х1 = - 3, х2 = 1
№ 45.9(б) х2 - 4х = – 3
y = x²; y = 4х – 3
Ответ: х1 = 1, х2 = 3
9.
Домашнее задание:№ 45.2, 45.3, 45.5, 45.9 –
оставшиеся пункты



 Математика
Математика








