Похожие презентации:
Функция. Прямая пропорциональность
1.
ФункцияПрямая пропорциональность. y =kx
Обратная пропорциональность.
Безгодкова О.В.
k
y= x
2.
Функция - одно из важнейших понятий математики, исходное понятиеведущей ее области - математического анализа. В школьном курсе
математики основное внимание уделяется числовым функциям.
В начальном курсе математики понятие функции и все, что с ним
связано, в явном виде не изучается, но идея функциональной зависимости
буквально пронизывает его, а правильное понимание таких свойств реальных
явлений, как взаимозависимость и изменяемость, является основой научного
мировоззрения. Безусловно, все это требует от учителя начальных классов
определенных знаний о функции и ее свойствах
3.
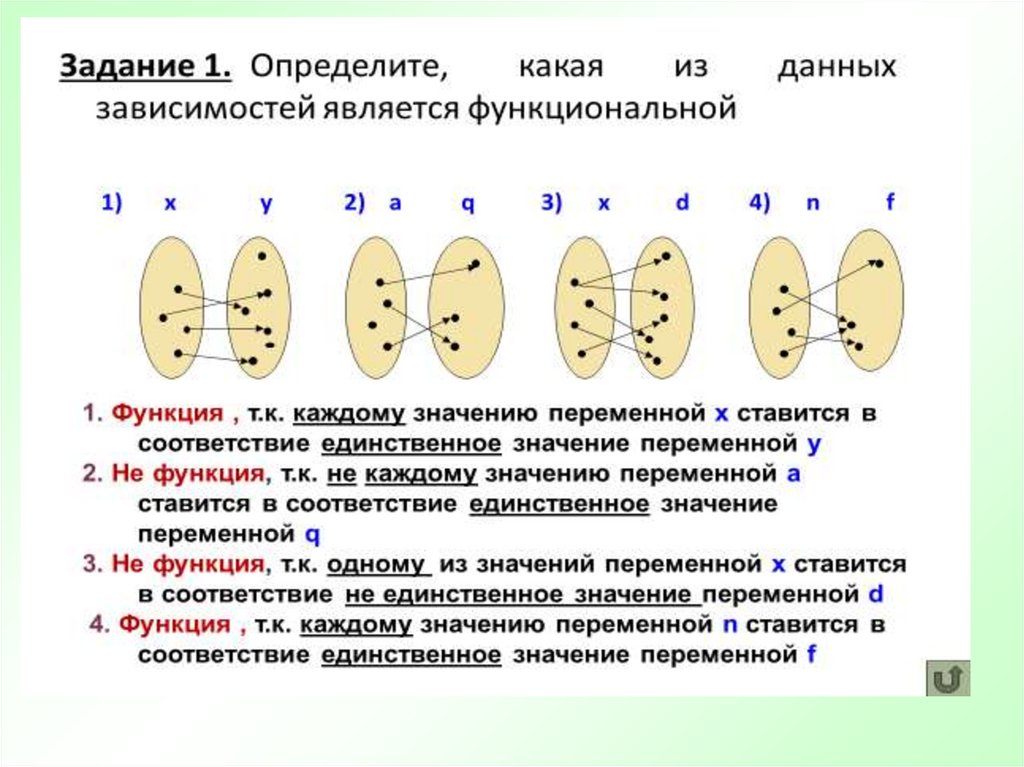
1. Понятие функции. Способы задания функцийОпределение. Числовой функцией называется такое соответствие между числовым
множеством X и множеством R действительных чисел, при котором каждому числу из
множества X сопоставляется единственное число из множества R.
Множество X называют областью определения функции.
Функции принято обозначать буквами f, g, h и др. Если f- функция, заданная на
множестве X, то действительное число у, соответствующее числу x из множества X, часто
обозначают f(х) и пишут у = f(х). Переменную х при этом называют аргументом (или
независимой переменной) функции f. Множество чисел вида f(х) для всех х из множества X
называют областью значений функции f.
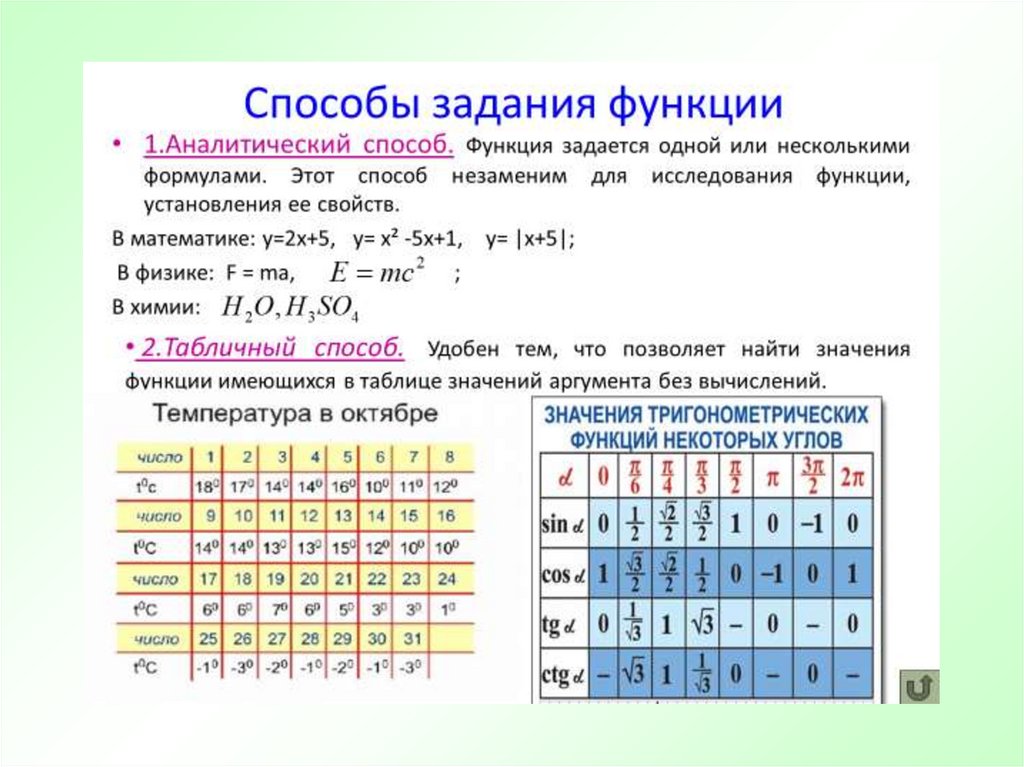
Из определения функции вытекает, что для задания функции необходимо указать,
во-первых, числовое множество X, т.е. область определения функции, и, во-вторых,
правило, по которому каждому числу из множества X соответствует единственное
действительное число.
4.
Что такое функция?Определение: Числовой функцией называется такой закон f,
при котором каждому числу х из множества D
ставится в соответствие единственное число у, зависящее от х.
т.е. задана функция y=f(x) с областью определения D
Обозначают: у = f(x), x Є D.
Переменную х называют аргументом.
Переменную у – функцией.
f
D
Х
f(x)
у
у1
5.
6.
7.
8.
9.
10.
11.
Свойство монотонности функцииЧисловые функции обладают многими свойствами. Мы рассмотрим одно из них - свойство
монотонности, так как понимание этого свойства учителем важно при обучении
математике младших школьников.
Определение. Функция f(х) называется монотонной на некотором
промежутке А, если она на этом промежутке возрастает или убывает.
Определение. Функция f(х) называется возрастающей на некотором
промежутке А, если для любых чисел х1, х2 из множества А выполняется условие:
х1< х2 f(х1)< f(х2)
Определение. Функция f называется убывающей на некотором промежутке
А, если для любых чисел х1, х2 из множества А выполняется условие:
х1< х2 f(х1)> f(х2)
12.
Прямая пропорциональностьОпределение. Прямой пропорциональностью называется функция, которая
может быть задана при помощи формулы у = kх, где k - не равное нулю
действительное число.
Название функции у = kх связано с тем, что в формуле у = kх есть переменные х и
у, которые могут быть значениями величин. А если отношение двух величин равно
некоторому числу, отличному от нуля, их называют прямо пропорциональными. В
нашем случае y/x = k (k ≠ 0). Это число называют коэффициентом
пропорциональности.
Функция у = kх является математической моделью многих реальных ситуаций,
рассматриваемых уже в начальном курсе математики.
Если t - время движения пешехода (в часах), s - пройденный путь (в километрах), и
он движется равномерно со скоростью 4 км/ч, то зависимость между этими величинами
можно выразить формулой s = 4t. Так как каждому значению I соответствует
единственное значение 5, то можно говорить о том, что с помощью формулы s = 4t
задана функция.
13.
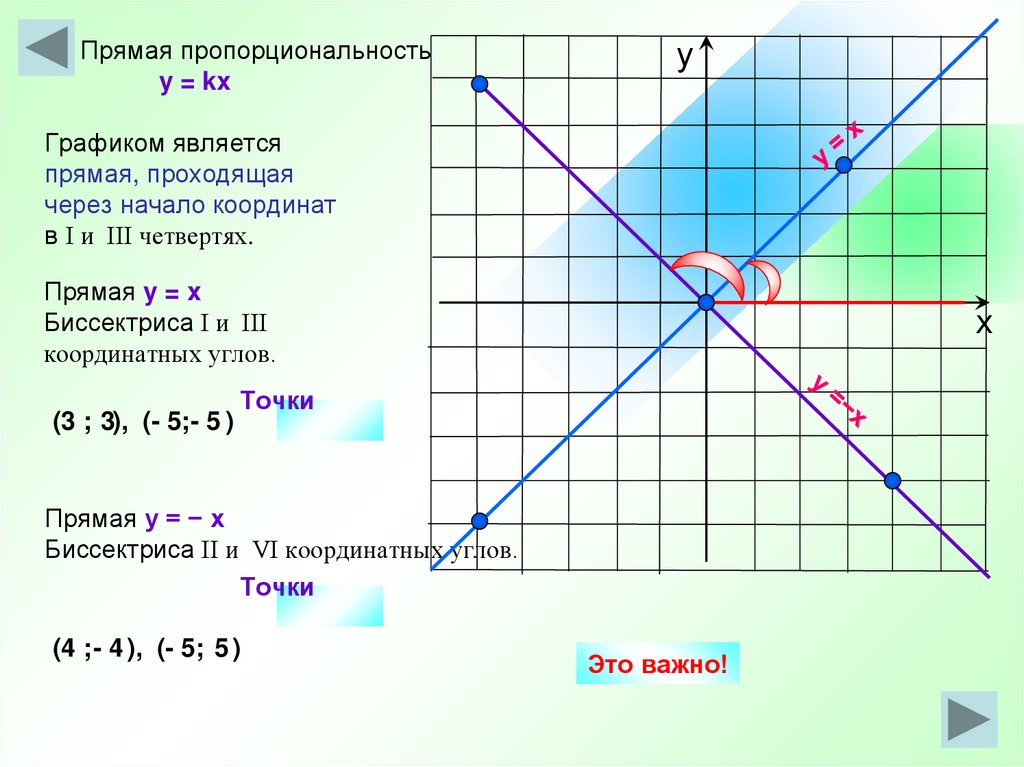
Прямая пропорциональностьy = kx
у
Графиком является
прямая, проходящая
через начало координат
в I и III четвертях.
Прямая y = x
Биссектриса I и III
координатных углов.
(3 ; 3), (- 5;- 5 )
х
Точки
Прямая y = − x
Биссектриса II и VI координатных углов.
Точки
(4 ; - 4 ), (- 5; 5 )
Это важно!
14.
Свойства прямой пропорциональности1. Областью определения функции у = kх и областью ее значений является множество
действительных чисел.
2. Графиком прямой пропорциональности является прямая, проходящая через начало
координат. Поэтому для построения графика прямой пропорциональности достаточно
найти лишь одну точку, принадлежащую ему и не совпадающую с началом
координат, а затем через эту точку и начало координат провести прямую.
Например, чтобы построить график функции у = 2х, достаточно иметь точку с координатами (1, 2), а затем через нее и начало координат провести прямую (рис. 89).
3. При k > 0 функция у = kх возрастает на всей области определения; при k < 0 убывает на всей области определения.
4. Если функция f - прямая пропорциональность и (х1,у1), (х2,у2),
соответственных значений переменных x и у, причем x2 ≠ 0, то x1/x2 = y1/y2
- пары
15.
Обратная пропорциональностиОпределение. Обратной пропорциональностью называется функция, которая
может быть задана при помощи формулы у = k/x, где k – не равное нулю
действительное число.
Название данной функции связано с тем, что в у = k/x есть переменные x и у, которые
могут быть значениями величин. А если произведение двух величин равно некоторому
числу, отличному от нуля, то их называют обратно пропорциональными. В нашем случае
xy = k (к ≠ 0). Это число k называют коэффициентом пропорциональности.
Функция у = k/x является математической моделью многих реальных ситуаций,
рассматриваемых уже в начальном курсе математики.
Если t- время движения пешехода (в часах), v - его скорость (в км/ч) и он прошел 12 км, то
зависимость между этими величинами можно выразить формулой v · t = 20 или v= 20/t. Так как
каждому значению t (t≠0) соответствует единственное значение скорости v, то можно говорить о
том, что с помощью формулы v =20/t задана функция.
16.
уОбратная пропорциональность
k>0
Графиком является гипербола,
проходящая в I и III четвертях.
Гипербола в
I и III координатных четвертях.
Точки
х
у
-0,5
-4
-1
-2
4
-
-2
- 1 - 0,5
х
17.
18.
Свойства обратной пропорциональности1. Областью определения функции у = k/x и областью ее значений x является
множество действительных чисел, отличных от нуля.
2. Графиком обратной пропорциональности является гипербола.
3. При k > 0 ветви гиперболы расположены в 1-й и 3-й четвертях и функция у = k/x
является убывающей на всей области определения x (рис. 90). При k < 0 ветви
гиперболы расположены во 2-й и 4-й четвертях и функция у = k/x является
возрастающей на всей области определения х
4. Если функция f - обратная пропорциональность и (х1,у1), (х2,у2) - пары
соответственных значений переменных х и у, то x1/x2 = y1/y2.
19.
Укажите, какие из функций являются прямой иобратной пропорциональностью.
3
у ;
х
х
у ;
5
у = 2х – 1;
1
у х;
4
7
у ;
х
0,6
у
;
х
5
у 2;
х
1
у
2х
















 Математика
Математика








