Похожие презентации:
Физические основы механики
1. Курс лекций по общей физике Раздел 1. Физические основы механики Разработчик: к.п.н., доцент кафедры САПРиМ Соболева В.В.
16.12.2023ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ АСТРАХАНСКОЙ ОБЛАСТИ
«АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ
УНИВЕРСИТЕТ»
Кафедра «Системы автоматизированного
проектирования и моделирования»
Курс лекций по общей физике
Раздел 1. Физические основы
механики
Разработчик: к.п.н., доцент кафедры САПРиМ
Соболева В.В.
1
2. Общая структура изучаемого курса:
16.12.2023Общая структура изучаемого курса:
1
2
Физические основы механики.
Молекулярная физика и термодинамика.
Электрическое поле.
Колебания и волны. Оптика. Физика атомов
и молекул.
2
3. Литература:
1.2.
3.
4.
5.
6.
Трофимова Т.И. Курс физики. М.: Академия, 2012 г., 537 с.
Трофимова Т.И. Краткий курс физики с примерами решения задач.М.: Кнорус, 2007 г., 279 с.
Детлаф А.А., Яворский Б.М. Курс физики. - М.: Высшая школа, 1989
Черноуцан А.И. Краткий курс физики: учебное пособие/А.И.
Черноуцан. – М.: Физматлит, 2002 г., 309с. [Электронный ресурс]. –
URL:
http://biblioclub.ru/index.php?page=book_view_red&book_id=82664
Сивухин Д.В. Общий курс физики: учебное пособие: в 5 т. Т.1.
Механика. – 6-е изд., стеорт. – М.: ФИЗМАТЛИТ, 2014. – 560 с.
[Электронный ресурс]. – URL:
http://biblioclub.ru/index.php?page=book_view_red&book_id=275610
Зисман Г.А., Тодес О.М. Курс общей физики. - М.: Высшая
школа,1989, т. 1
16.12.2023
3
4. 1.1 Кинематика материальной точки и поступательного движения твердого тела
Физические модели в механике:Материальной точкой (тело точечной массы)
называется идеализированная модель, соответствующая
физическому телу, размерами которого в данных
условиях можно пренебречь.
Абсолютно твердое тело – тело, расстояние между
двумя точками которого в условиях данной задачи
можно считать постоянным. Иначе говоря - это тело,
формы и размеры которого не изменяются при его
движении.
16.12.2023
4
5. Физические модели в механике:
Абсолютно упругое тело – тело, деформациякоторого подчиняется закону Гука, а после
прекращения внешнего силового воздействия
восстанавливает свои первоначальные размеры и
форму
Абсолютно неупругое тело – тело, сохраняющее
деформированное состояние после прекращения
действия внешних сил.
16.12.2023
5
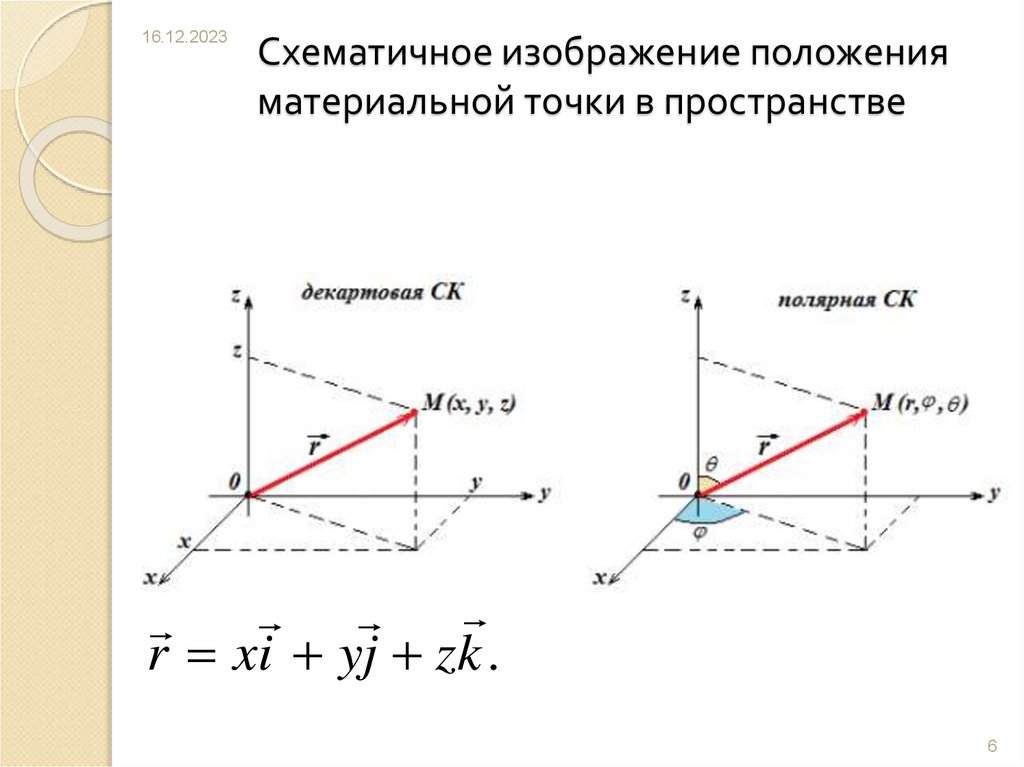
6. Схематичное изображение положения материальной точки в пространстве
16.12.2023Схематичное изображение положения
материальной точки в пространстве
r xi yj zk .
6
7. Основные понятия и определения
Траектория движенияДлина пути
Вектор перемещения
• Скорость
• Ускорение
r r2 r1 r (t2 ) r (t1 )
x i y j z k вектор перемещения
16.12.2023
7
8. Вектор средней скорости
rср
t
16.12.2023
8
9. Мгновенная скорость
r drlim
t 0 t
dt
16.12.2023
9
10. Вектор скорости
dr dxi yj zk
dt dt
dx
dy
dz
i
j k
dt
dt
dt
16.12.2023
10
11. Модуль вектора скорости
2x
2
2
y
2
z
2
2
dx dy dz
.
dt dt dt
16.12.2023
11
12. Ускорение
a tУскорение
ср
16.12.2023
12
13. мгновенное ускорение
da lim a ср lim
t 0
t 0 t
dt
16.12.2023
13
14. Вектор ускорения
d dx dy dza i j k
dt dt dt
dt
y
d
d
x
d
z
.
j
i
k
dt
dt
dt
2
2
2
2
2
16.12.2023
2
14
15.
Модуль вектора скоростиa a a a a
2
2
2
x
y
z
2
2
2
d x d y d z
.
dt 2 dt 2 dt 2
2
2
16.12.2023
2
15
16.
Движение материальной точки вдолькриволинейной траектории
16.12.2023
16
17. Ускорение материальной точки
d da
dt dt
d
d
.
dt
dt
16.12.2023
17
18. Ускорение материальной точки при криволинейном движении
1)тангенциальное ускорение:
d
a
,
dt
2) нормальное ускорение :
d
an
.
dt
16.12.2023
18
19. Полное ускорение материальной точки
a a a2
n
dv v
a a a .
dt R
2
4
2
2
n
16.12.2023
19
20. 1. Прямолинейное равномерное движение
consta 0, a 0
n
0
t
x dt x t x ,
x
0
0
0
.
t
S x x0
16.12.2023
20
21. 2. Прямолинейное равнопеременное движение
ta dt a t ,
0
0
0
t
t
0
0
a t
x x0 dt x0 0 a t dt x0 0 t
2
a
t
S x x t
2
0
2
0
16.12.2023
21
2
22. 3. Равномерное движение по окружности
an2
R
16.12.2023
22
23. Кинематика вращательного движения
16.12.202323
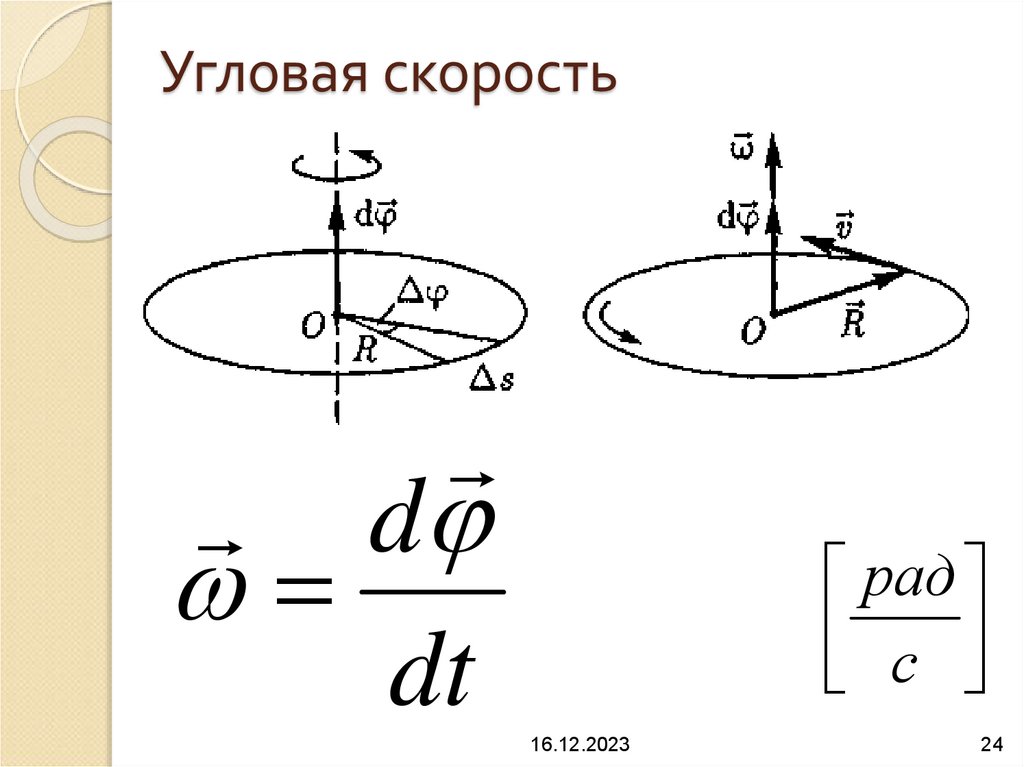
24. Угловая скорость
ddt
рад
с
16.12.2023
24
25. Угловое ускорение:
16.12.2023d
dt
25
26. Уравнения кинематики вращательного движения твердого тела
а) Равномерное вращение:0 , const
t
dt t
0
0
0
16.12.2023
26
27. Уравнения кинематики вращательного движения твердого тела
б) Равнопеременное вращение относительнооси OZ:
t
0 z dt 0 z t
const
0
t
t
0
0
0 dt 0 ( 0 z t ) dt
0 0t
zt
2
2
d
S dt Rdt R dt R
dt
t1
t1
t1
t2
t2
t2
16.12.2023
27
28.
Динамические характеристики материальнойточки: сила, масса.
Законы Ньютона
16.12.2023
28
29.
СилыВнешние
Внутренние
Сила F задана:
•указан модуль F;
•направление в пространстве;
•точка приложения.
Единица измерения силы:
Ньютон [Н]
16.12.2023
29
30.
16.12.202330
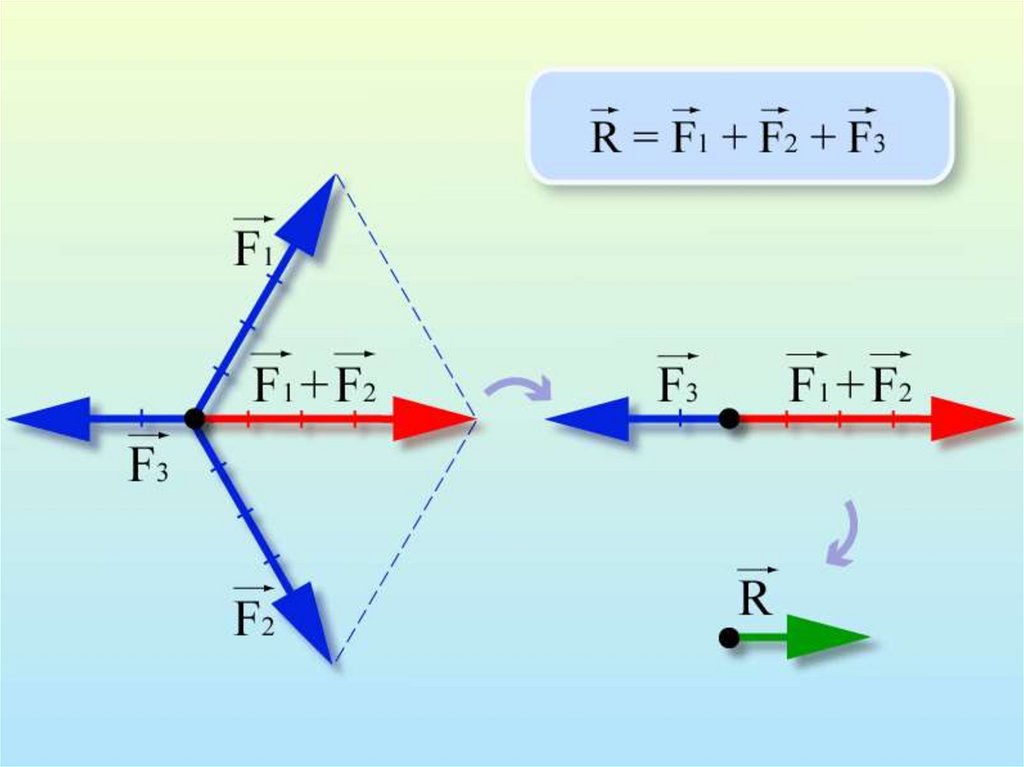
31. Равнодействующая сила:
...F
F F F
F
n
р
i 1
i
1
2
n
16.12.2023
31
32.
Свойства массы (m) тела:1) масса материальной точки не зависит от состояния
движения точки, являясь ее неизменной
характеристикой;
n
2) масса – величина аддитивная:
m mi
i 1
3) масса замкнутой системы остается неизменной при
любых процессах, происходящих в этой системе (закон
сохранения массы).
16.12.2023
32
33. Законы Ньютона
16.12.202333
34. Первый закон Ньютона:
Материальнаяточка
сохраняет
состояние покоя или равномерного и
прямолинейного движения до тех пор,
пока воздействие со стороны других тел
не заставит его изменить это состояние
16.12.2023
34
35. Второй закон Ньютона
Fa
m
16.12.2023
35
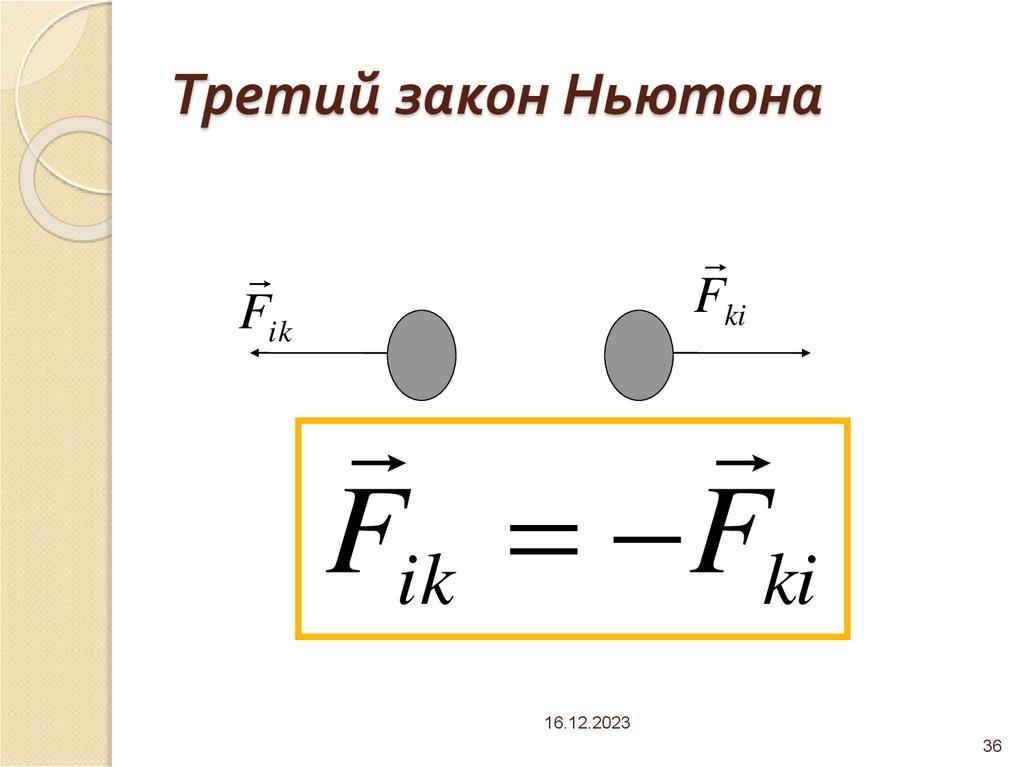
36. Третий закон Ньютона
FkiFik
Fik Fki
16.12.2023
36
37. Силы в природе
38. Силы всемирного тяготения (гравитационные силы)
Закон всемирного тяготения:m1 m 2
F G
2
R
G = 6,672·10-11 Н·м2/кг2 – гравитационная постоянная
39.
Ускорение свободного паденияmM 3
mg G 2
R3
Mз
g G 2 .
Rз
g G
Mз
R h
2
з
.
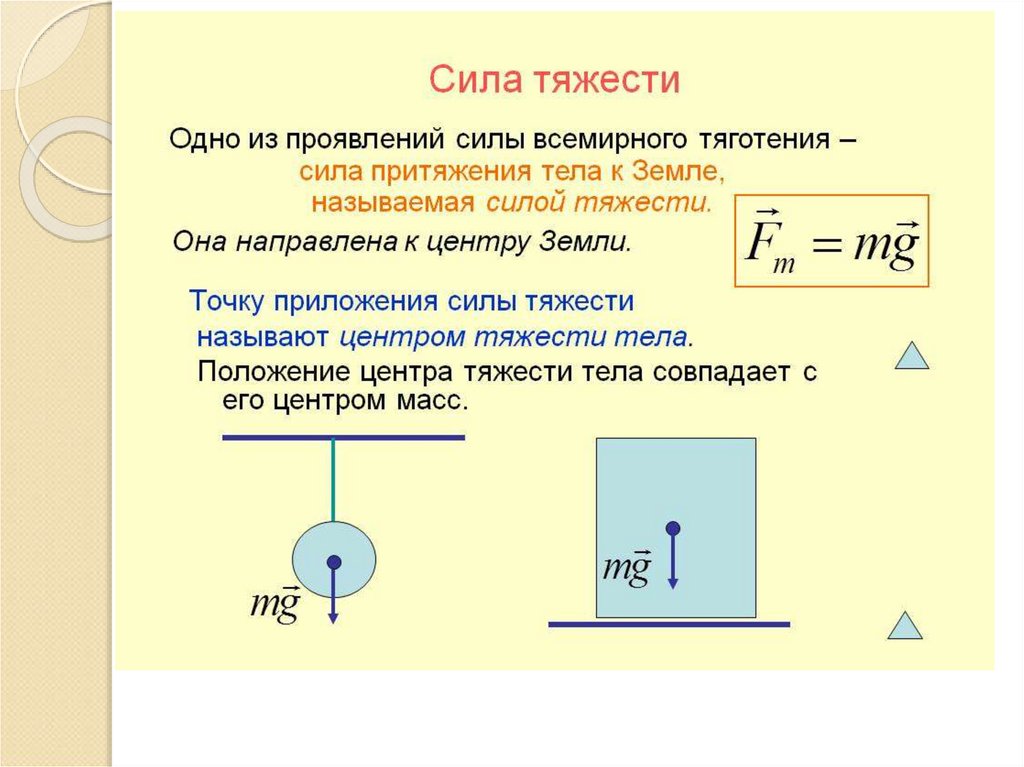
40.
41. Вес тела
42.
Сила тренияFтр N
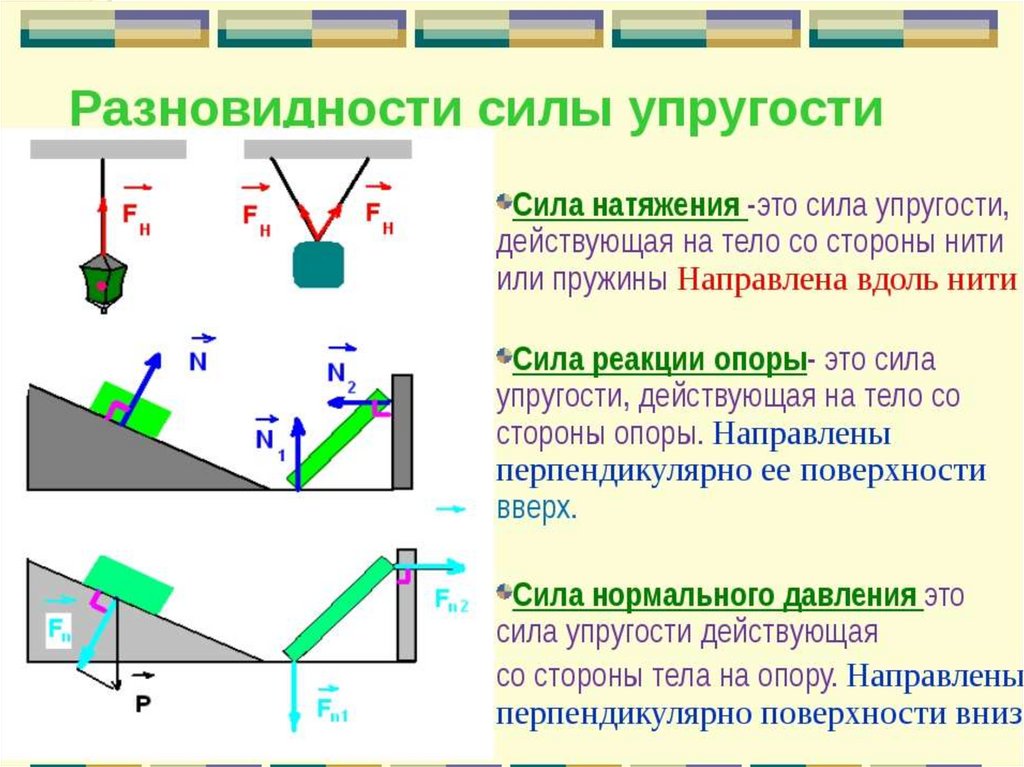
43. Сила упругости
Упругой деформацией называют такуюдеформацию, которая исчезает после
прекращения действия приложенных сил
Пластической или остаточной
деформацией называют такую
деформацию, которая имеет место и после
прекращения действия сил
44. Сила упругости
45.
46. Закон Гука
E47.
lм одульот носит ельной деформ ации
lo
l l lo
F
S
- модуль абсолютной деформации
- механическое напряжение
48. Коэффициент Пуассона: отношение относительного поперечного сжатия стержня к его относительному продольному удлинению
(деформации):a l
:
a0 l
49. Работа. Мощность. Энергия. Импульс
16.12.202349
50.
Работа(А)
A F dr F dt ,
A lim
Fi ri F dr
n
r 0
r
i 1
l
l
0
0
А F cos dl Fl dl.
Единица измерения: джоуль [ Дж]
16.12.2023
50
51.
ВЫВОДЫ1) работа обладает свойством аддитивности;
2) если /2> >0, то cos >0 – работа
положительна;
3) если = /2, то работа равна нулю;
4) если > > /2, то работа совершается против
действия силы и она отрицательна;
5) «центростремительная» сила (например, сила
Лоренца) не совершает работы.
16.12.2023
51
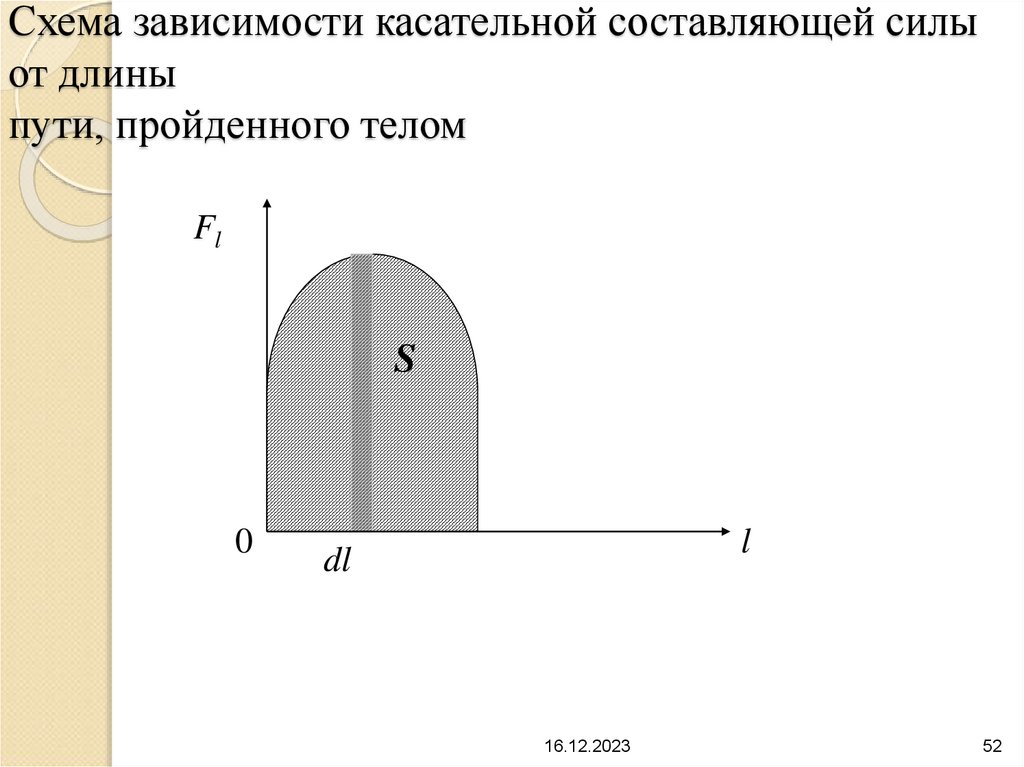
52. Схема зависимости касательной составляющей силы от длины пути, пройденного телом
FlS
0
l
dl
16.12.2023
52
53. Мощность силы в поступательном движении
NA
dt
16.12.2023
53
54. Мощность силы в поступательном движении
dlN F cos F cos
dt
N F v cos Fl v F v
16.12.2023
54
55. Вывод формулы кинетической энергии поступательно движущегося тела
A Fl dld
Fl m
dt
16.12.2023
55
56. Вывод формулы кинетической энергии поступательно движущегося тела
ddl
A m
dl m d
dt
dt
A m d
16.12.2023
56
57. Вывод формулы кинетической энергии поступательно движущегося тела
mA m d
2
0
m
Wk A
2
16.12.2023
2
2
57
58. Потенциальная энергия
A1-2 = Wп1 - Wп2H
l
mg
A = P l cos = m g H
16.12.2023
58
59.
Работа силы тяжестина криволинейном пути
n
n
i 1
i 1
A Ai P H i P H m g H
Wп = m g H + Wп0
Wп = m g H
16.12.2023
59
60. Полная механическая энергия системы:
W = Wк + Wп16.12.2023
60
61. Импульс (количество движения) материальной точки
р mкг м
с
16.12.2023
61
62. Основное уравнение динамики поступательного движения материальной точки
d d m dрm a m
dt
dt
dt
dр
F
dt
dр F dt
16.12.2023
62
63. Следствие из основного уравнения динамики поступательного движения
1. F constt
р F dt m 0 F t р0
0
2. F const ,
m 2 m 1 F dt Fср t2 t1
t2
t1
16.12.2023
63
64. Законы сохранения в механике:
Закон сохранения количествадвижения (импульса) тела
Закон сохранения
механической энергии
Закон сохранения момента
импульса
16.12.2023
64
65. Закон сохранения импульса
dрd
m
0
рx = const
dt
dt
р mi i const
n
i 1
16.12.2023
65
66. Применение закона сохранения импульса
Абсолютно неупругий ударm1
m2
1
m1+т2
2
а)
u
б)
Рис.
Схематическое изображение неупругого удара двух тел:
а) состояние до удара; б) после удара
m1 1 m2 2
u
.
m1 m2
16.12.2023
66
67. Закон сохранения и превращения энергии в механике
в замкнутой системе энергия можетпереходить из одних видов в другие и
передаваться от одного тела к
другому, но ее общее количество
остается неизменным
16.12.2023
67
68. закон сохранения механической энергии
W = Wк + Wп = constполная механическая энергия консервативной системы
не изменяется с течением времени
16.12.2023
68
69. применение закона сохранения механической энергии
б)а)
m1
1
m2
2
m1
m2
u1
u2
Рис. 3.7.
Схематическое изображение упругого прямого удара двух тел:
а) состояние до удара; б) после удара
m1 v1 m2 v2 m1 u1 m1 u 2
m1 v12 m2 v22 m1 u12 m2 u22
2
2
2
2
16.12.2023
69
70. Применение законов сохранения импульса и механической энергии (продолжение)
v1 m1 m2 2m2 v2u
1
m1 m2
u v2 m2 m1 2m1v1
2
m1 m2
16.12.2023
70
71. Закон сохранения момента импульса
внешM
0
dL z
0
dt
Lz const
I z const.
16.12.2023
71
72. Элементы механики твердого тела. Работа, мощность и энергия вращательного движения
73. Момент импульса
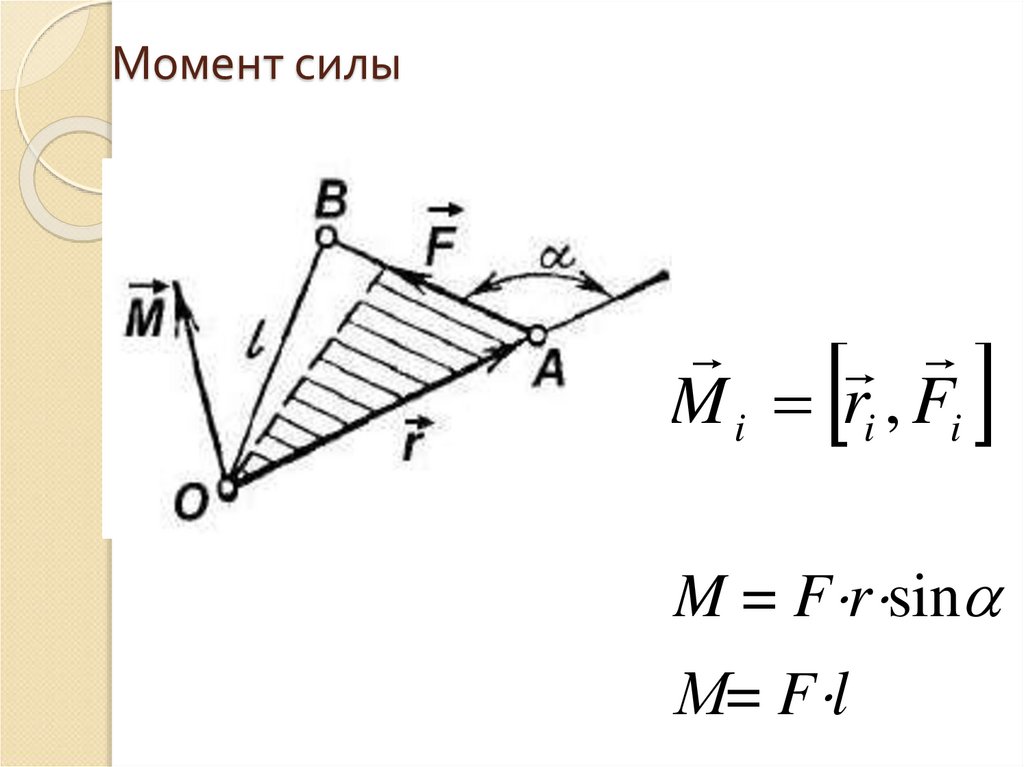
L r , mv74. Момент силы
M i ri , FiM = F r sin
М= F l
75. Момент инерции тела
76.
77. Теорема Штейнера (теорема о переносе осей инерции)
O/1O1
I = IC + m d2
C
O
d
O/
Теорема Штейнера: момент инерции тела I относительно
произвольной оси ОО1 равен сумме момента инерции тела
IC относительно оси O/O/1, проведенной через центр
инерции тела параллельно оси ОО1 и произведения массы
m тела на квадрат расстояния между этими осями
78.
Основное уравнение динамикивращательного движения
твердого тела
внеш
dL
M
.
dt
dL
d
I
I M
dt
dt
79. Второй закон Ньютона во вращательном движении
в нешMz
.
Jz
Угловое ускорение твердого тела, вращающегося
относительно неподвижной оси OZ, прямо
пропорционально результирующему моменту
(относительно этой оси) действующих на тело всех
внешних сил, и обратно пропорционально моменту
инерции тела относительно той же оси
80. Работа, совершаемая за конечный промежуток времени при вращательном движении
00
0
A A M z cos d M z d .
81. Мощность силы во вращательном движении
A M z d dN
Mz
dt
dt
dt
N M z
82. Кинетическая энергия вращающегося тела
вращk
W
I z
m
i
2 i 1
2
Wk W
2
вращ
k
n
2
i
m v
I z
.
2
2
2
C
2
2










































































 Физика
Физика








