Электричество и магнетизм

1.

company name
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

2.

Электростатика
Электростатика
рассматривает
неподвижные заряды и связанные с ними
неизменные электрические поля
Электрон, заряд – свойство материальных
объектов,
приводит
к
электрическим
взаимодействиям
2 типа зарядов
q
q
q 1Кл 1A 1c
Свойства электрического заряда
q Ne
e 1,6 10 19 Кл
1) эл. заряд – дискретная величина
Элементарный эл. заряд
Минимальный эл. заряд, заряды всех элементарных частиц, ядер
атомов, тел кратны элементарному заряду.
company name
2) закон сохранения эл. заряда
В электрически изолированной системе, т.е. в
системе, которая не обменивается зарядами с
внешними телами, алгебраическая сумма эл.
зарядов является величиной постоянной.
qi const

3.

Электростатика
3) инвариантность эл. заряда
Величина эл. заряда не зависит от скорости его
q f
движения, даже при движении со скоростями
близкими к скорости света.
Закон Кулона
(закон взаимодействия точечных зарядов) 1785 г.
V
Точечный заряд – заряженное тело, размерами которого можно
пренебречь по сравнению с расстояниями от него до других тел.
company name
Сила
электростатического
взаимодействия
двух
неподвижных
точечных зарядов в вакууме прямо
пропорциональна произведению модулей
этих зарядов и обратно пропорциональна
квадрату расстояния между ними.
Сила
направлена
по
прямой,
соединяющей заряды, и соответствует
притяжению для разноименных зарядов
и отталкиванию для одноименных.

4.

Электростатика
q1q2 r 1,2
F 1,2 k 2
r1,2 r1,2
r 1,2
q1q2
F 1,2 k 2
r1,2
- радиус-вектор, проведенный из первого заряда во второй
2
Н
м
k - постоянная закона Кулона k 9 109
2
Кл
2
1
Кл
, 0 - электрическая постоянная
k
0 8,85 10 12
Н м2
4 0
company name
В диэлектриках взаимодействие зарядов уменьшается за счет явления
поляризации.
диэлектрическая
проницаемость
среды,
показывает во сколько раз взаимодействие зарядов
в диэлектрике меньше по сравнению с их
взаимодействием в вакууме
Fв вакууме
Fв среде
q1q2
F 1,2 k 2
r1,2

5.

Электростатика
Электростатическое поле и его характеристики
Электростатическое поле – постоянное во времени электрическое поле,
создается неподвижными электрическими зарядами, является формой
материи, осуществляющей взаимодействие между электрическими
зарядами.
Характеристики электростатического поля
E - напряженность поля (силовая характеристика)
- потенциал поля (энергетическая характеристика)
Напряженность
поля
–
векторная
физическая
величина,
измеряемая
отношением
силы,
действующей
на
неподвижный
пробный
электрический заряд, к величине этого заряда.
company name
Направление вектора напряженности совпадает с направлением вектора
силы, действующей на помещаемый в данную точку поля пробный заряд.
qпр - пробный заряд, малый по величине, положительный точечный
заряд
E
F
qпр
E
Н В
Кл м
F qE
- кулоновская сила

6.

Электростатическое поле и его характеристики
Потенциал электростатического поля – скалярная физическая величина,
равная отношению потенциальной энергии пробного заряда в данной
точке поля к величине этого заряда.
Wпот
qпр
Wпот q
Дж
В
Кл
потенциальная энергия заряда
Как и потенциальная энергия потенциал электростатического поля
зависит от выбора нулевого уровня (т.е. той точки , в которой потенциал
считается равным нулю) и поэтому определен лишь с точностью до
произвольной постоянной.
company name
Wпот 0
Будем считать потенциальную энергию заряда и
потенциал в бесконечно удаленной точке равным
0
нулю:
Тогда потенциал данной точки поля равен работе, которую совершают
силы поля, перемещая единичный положительный заряд из данной точки
в бесконечно удаленную точку:
A W
W
1,
пот 1 пот
Wпот 1 q 1 Wпот 0 1
Wпот 1
q
A1,
q

7.

Электростатическое поле и его характеристики
Напряженность поля точечного заряда - физическая
определяемая
силой,
действующей
на
пробный
положительный заряд, помещенный в эту точку поля :
F
E
qпр
F k
величина,
точечный
q qпр r
r 2 r
q
E т.з. k 3 r
r
1 q
Eт . з.
4 0 r 2
векторный вид
скалярный вид
company name
r - радиус-вектор, проведенный в данную точку
поля из заряда q, создающего поле;
r - расстояние между зарядом q и точкой, в
которой определяется вектор E.
Вектор
напряженности
в
любой
точке
электрического поля направлен вдоль прямой,
соединяющей эту точку и заряд.
Вектор напряженности всегда направлен
положительного заряда к отрицательному.
от

8.

Электростатическое поле и его характеристики
Потенциал поля точечного заряда равен работе, которую совершают
силы поля, перемещая единичный положительный заряд из данной
точки в бесконечно удаленную точку:
A1,
1
q
A1, F dl
F q E
1
1 E dl
1
пробного заряда
dl - элементарное перемещение
В любой точке этого поля на пробны точечный заряд
q’ действует сила F :
'
company name
F
dl cos dr - приращение радиус-вектора
Из рис. видно, что
1 qq
4 0 r 2
E dl E dl cos E dr

9.

Электростатическое поле и его характеристики
Интегрируем:
q
q
dr
1 E dl E dr
dr
2
2
4
r
4
r
0
0 1
1
1
1
q 1
q
1
4 0 r 1 4 0 r
q
т . з .
4 0 r
- потенциал поля точечного заряда
Связь напряженности и потенциала электростатического поля
company name
Эл. поле имеет две характеристики:
силовую – вектор напряженности поля
энергетическую – потенциал поля
E

10.

Электростатическое поле и его характеристики
Свяжем эти 2 характеристики друг с другом:
а) известна напряженность в любой точке поля
E f r f x, y, z
Потенциал находится интегрированием:
1 E dl Edl cos Edl
1
1
Разность потенциалов:
2
2
1,2 Edl E dl cos E , dl
1
1
company name
б) известен потенциал в любой точке поля
f r f x, y, z

11.

Электростатическое поле и его характеристики
Из сопоставления формул для потенциальной энергии и потенциала поля
точечного заряда, получаем
1 qqпр
Wпот
,
4 0 r
1 q
4 0 r
Wпот qпр
Сила, действующая на заряд в электростатическом поле:
F E qпр
Из механики известна связь между силой и потенциальной энергией:
F gradWпот
company name
Поскольку заряд
grad qпр E qпр
qпр не зависит от координат точек поля, получаем:
grad qпр qпр grad
E grad

12.

Электростатическое поле и его характеристики
Проекции вектора напряженности на оси координат запишутся в виде:
E x , E y , Ez
x
y
z
Представим вектор E через компоненты координат:
E E x i E y j Ez k i
j
k grad
y
z
x
Работа в электростатическом поле по перемещению заряда
company name
1 qqпр
F
4 0 r 2
При перемещении пробного заряда из т.1 в т.2 эта
сила совершает работу:
2
2
1
1
A1,2 F dl F dl cos , dl cos dr

13.

Электростатическое поле и его характеристики
qqпр 1 1
A1,2
2
4 0 1 r
4 0 r1 r2
qqпр 2 dr
Работа сил электростатического поля не зависит от
формы траектории, а зависит от начального и
конечного положения пробного заряда.
Силы, производящие такую работу, называются
потенциальными (или консервативными).
company name
1 qпр
4 0 r
qqпр 1 1
A1,2
q 1 2
4 0 r1 r2
A1,2 q 1 2
Работа сил электростатического поля равна произведению величины
заряда на разность потенциалов начальной и конечной точки.

14.

Электростатическое поле и его характеристики
Работа перемещения заряда в электростатическом
произвольной замкнутой траектории равна нулю:
поле
вдоль
A dA q нач кон 0 , т.к.
нач кон
Учитывая, что
dA F dl
F q E
q E dl 0
dA q E dl
Интеграл
E dl называется циркуляцией вектора напряженности.
L
company name
L
Циркуляция вектора напряженности в любом электростатическом поле
равна нулю. Это утверждение называют теоремой о циркуляции:
E dl 0
L

15.

Электростатическое поле и его характеристики
Принцип суперпозиции полей
Поле – вид материи, с помощью которого происходит взаимодействие
частиц вещества.
Принцип суперпозиции полей – поля существуют в пространстве
независимо друг от друга.
При наложении полей в одной точке пространства характеристики полей
складываются линейным образом.
Поле – переносчик взаимодействия между частицами (объектами), поля
друг на друга не действуют.
Пусть электростатическое поле создается системой зарядов:
n
F Fi
E
company name
i 1
F
q
n
E
F
i 1
q
i
n
n
Fi
Ei
i 1 q
i 1

16.

Принцип суперпозиции полей
n
i 1
Вектор напряженности поля системы зарядов равен
векторной сумме напряженностей полей, создаваемых
каждым из зарядов в отдельности.
E Ei
1 E dl Ei dl Ei dl i
i 1
i 1 1
1
1 i 1
i
i 1
Потенциал системы зарядов равен алгебраической
сумме потенциалов полей каждого заряда в
отдельности.
company name
Свойства потенциала электростатического поля
1) это скалярная величина
2) потенциал величина непрерывная, он не изменяется на границе
раздела двух заряженных сред
3) на бесконечности потенциал системы неподвижных стационарных
зарядов полагается равным нулю
4) для потенциала электростатического поля справедлив принцип
суперпозиции.

17.

Электростатическое поле и его характеристики
Графическое изображение электростатических полей
company name
Электростатическое поле наглядно изображают с помощью силовых
линий и эквипотенциальных поверхностей.
суперпозиции
Силовые линииПринцип
или линии
напряженности –полей
линии, касательные к
которым в любой точке совпадают с направлением вектора E в этой точке.
Принципы построения силовых линий:
1) силовые линии не пересекаются, начинаются
на положительных зарядах и заканчиваются
на отрицательных (или в бесконечности), т.е.
направлены от «+» к «-»
2) силовые линии вектора E подходят к
поверхности зарядов под прямым углом
3) для количественного описания вектора E
силовые линии проводят с определенной
густотой.
Число
линий
напряженности,
пронизывающих
единицу
площади
поверхности,
перпендикулярную
линии
напряженности,
должно
быть
равно
(пропорционально) модулю вектора E.

18.

Графическое изображение электростатических полей
company name
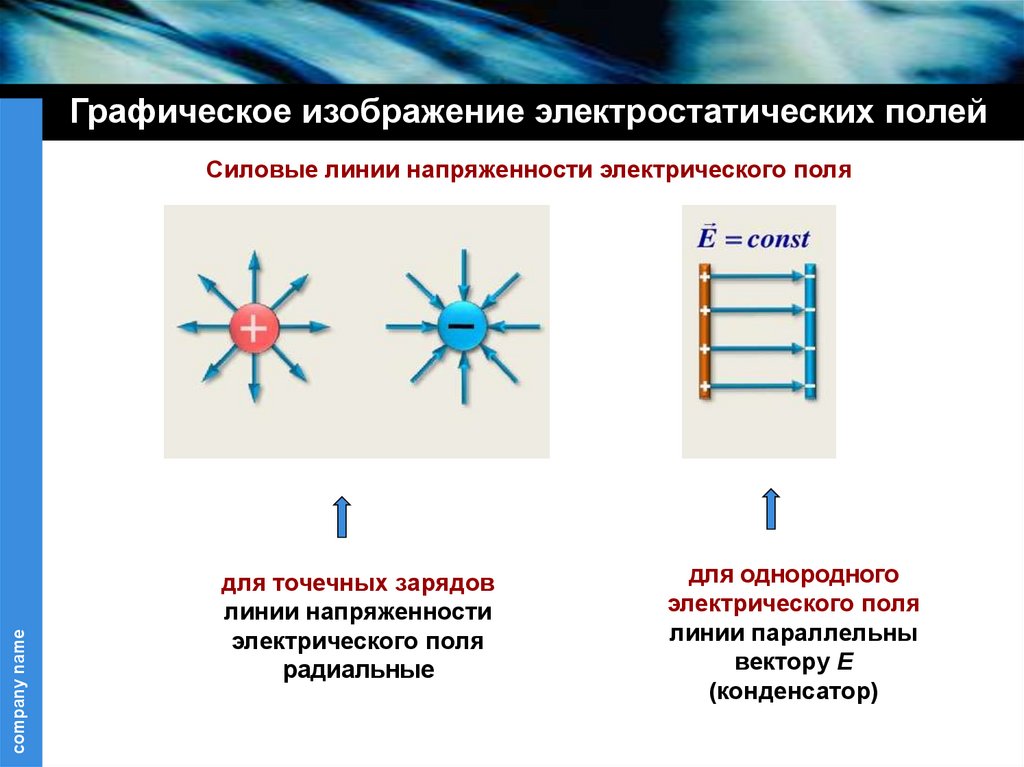
Силовые линии напряженности электрического поля
для точечных зарядов
линии напряженности
электрического поля
радиальные
для однородного
электрического поля
линии параллельны
вектору E
(конденсатор)

19.

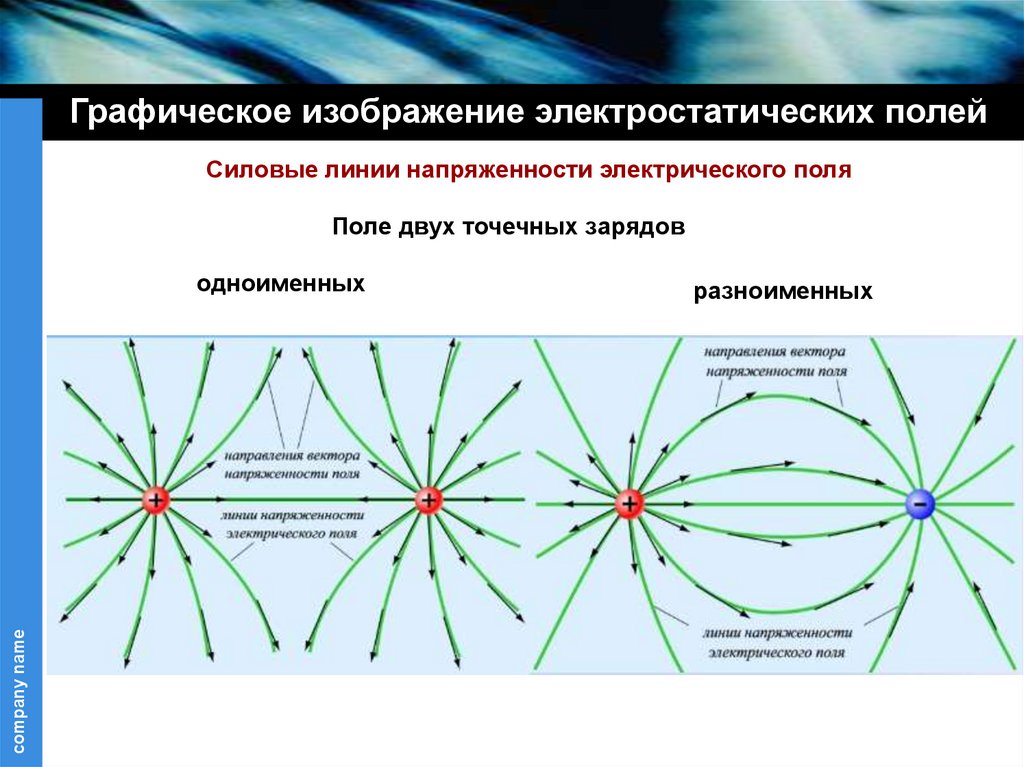
Графическое изображение электростатических полей
Силовые линии напряженности электрического поля
Поле двух точечных зарядов
company name
одноименных
разноименных

20.

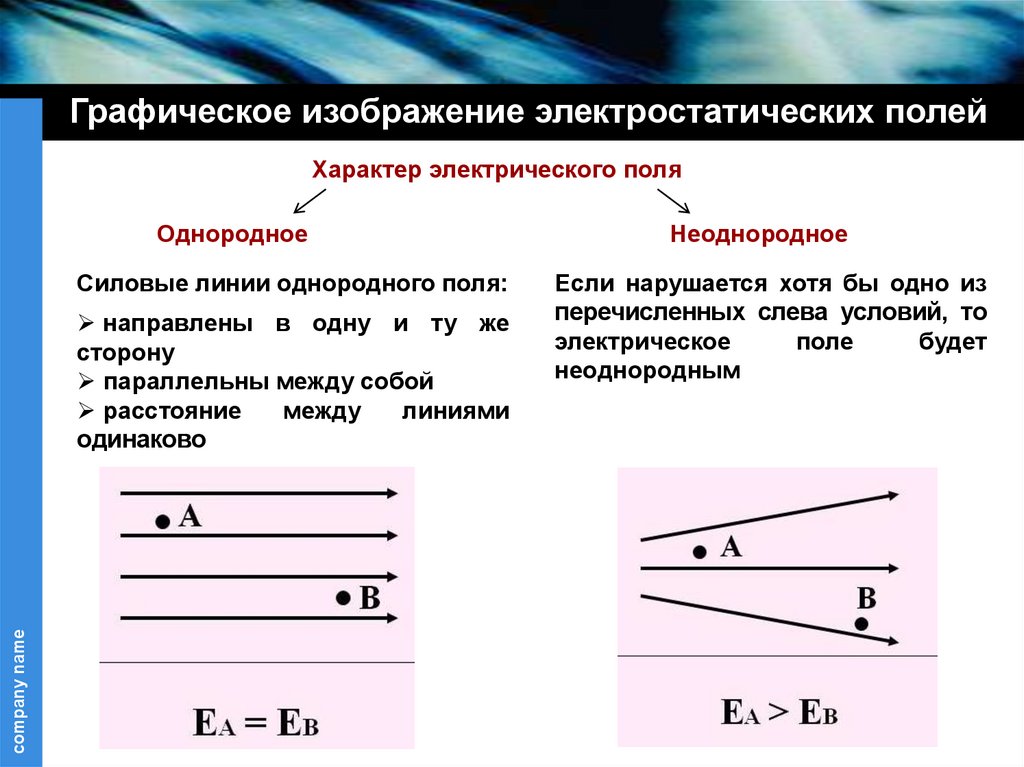
Графическое изображение электростатических полей
Характер электрического поля
Однородное
Силовые линии однородного поля:
company name
направлены в одну и ту же
сторону
параллельны между собой
расстояние
между
линиями
одинаково
Неоднородное
Если нарушается хотя бы одно из
перечисленных слева условий, то
электрическое
поле
будет
неоднородным

21.

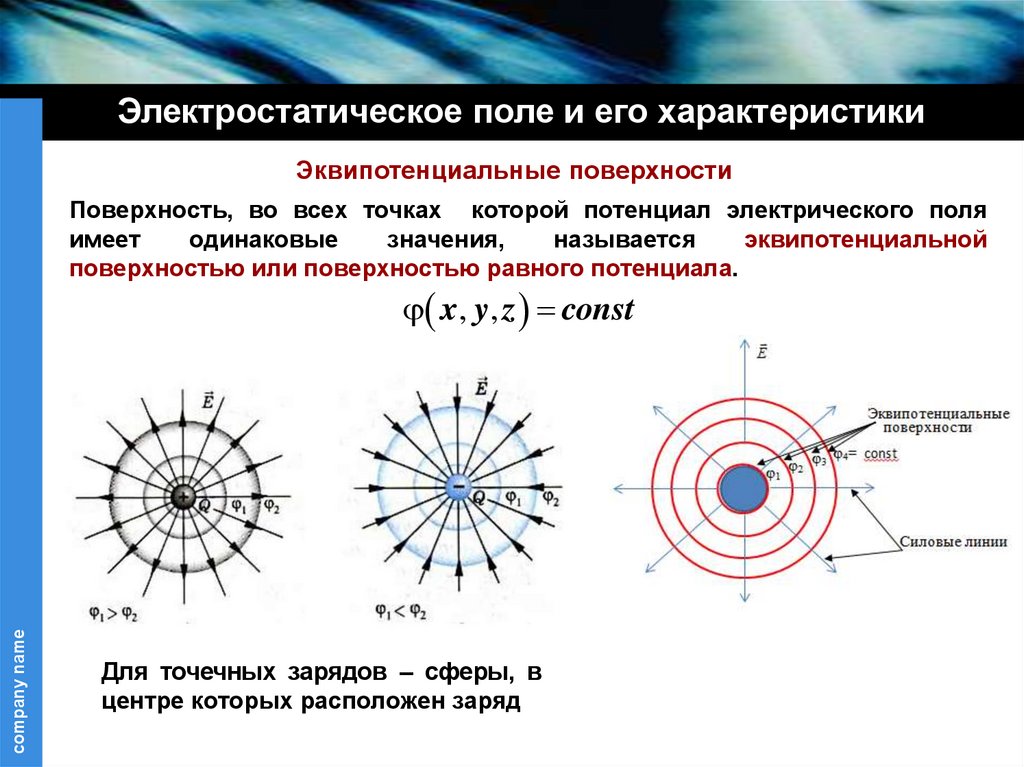
Электростатическое поле и его характеристики
Эквипотенциальные поверхности
Поверхность, во всех точках которой потенциал электрического поля
имеет
одинаковые
значения,
называется
эквипотенциальной
поверхностью или поверхностью равного потенциала.
company name
x, y, z const
Для точечных зарядов – сферы, в
центре которых расположен заряд

22.

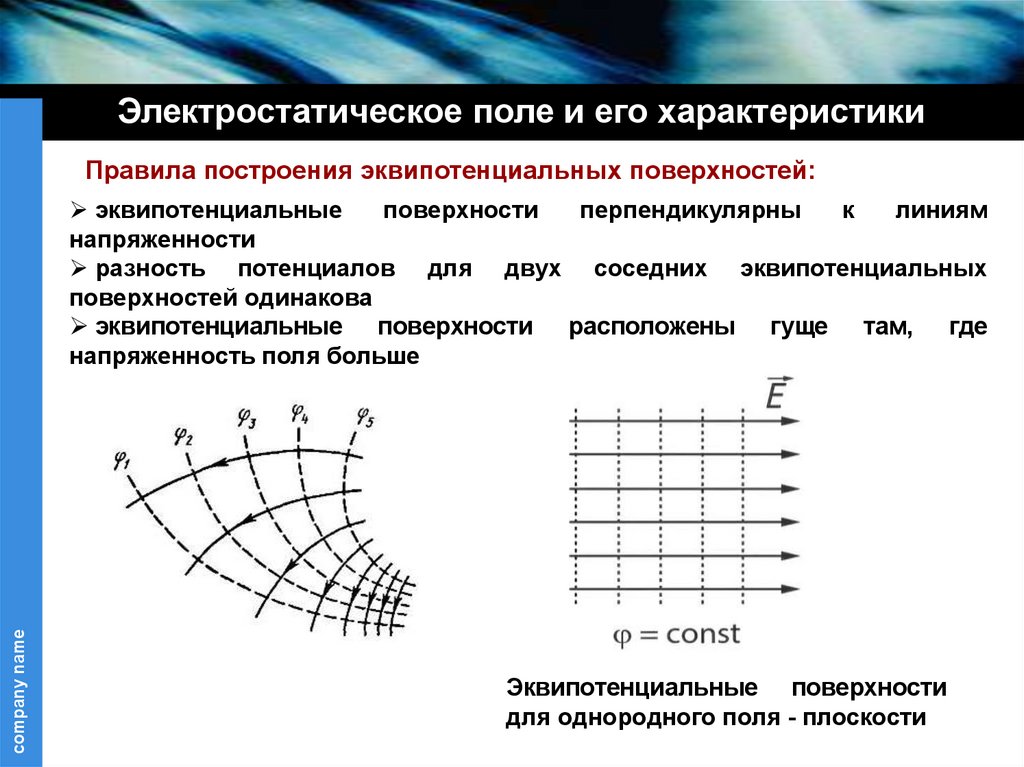
Электростатическое поле и его характеристики
Правила построения эквипотенциальных поверхностей:
company name
эквипотенциальные
поверхности
перпендикулярны
к
линиям
напряженности
разность потенциалов для двух соседних эквипотенциальных
поверхностей одинакова
эквипотенциальные поверхности расположены гуще там, где
напряженность поля больше
Эквипотенциальные поверхности
для однородного поля - плоскости

23.

Линии напряженности и эквипотенциальные поверхности
company name
Примеры:

24.

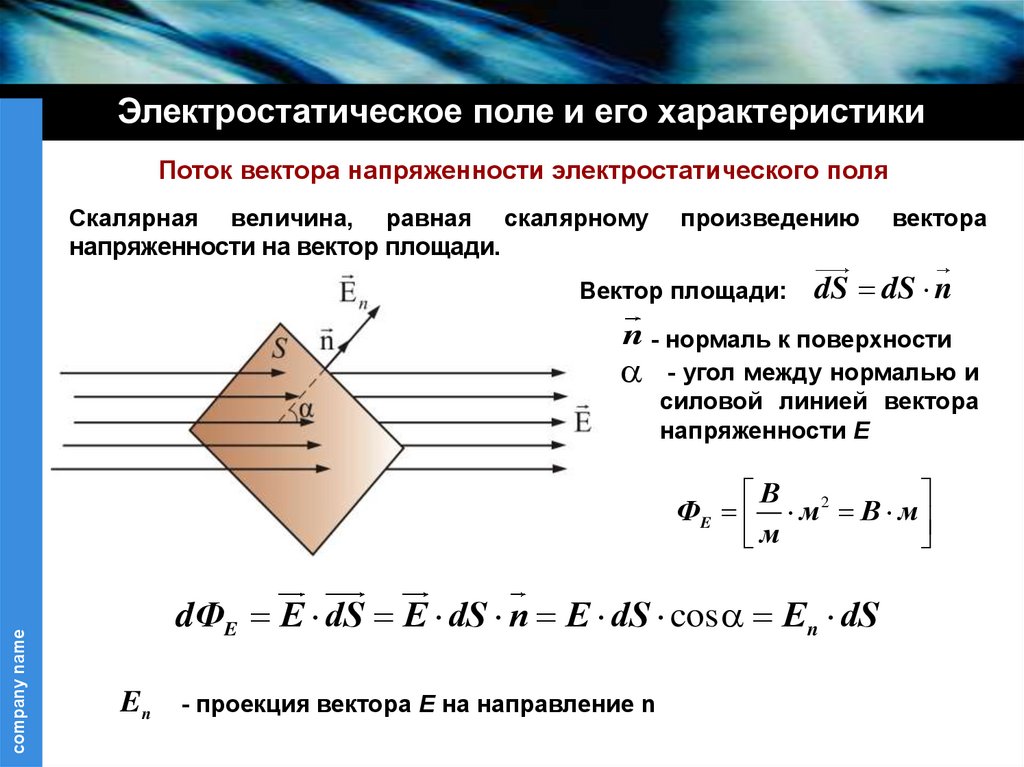
Электростатическое поле и его характеристики
Поток вектора напряженности электростатического поля
Скалярная величина, равная скалярному
напряженности на вектор площади.
произведению
Вектор площади:
вектора
dS dS n
n - нормаль к поверхности
- угол между нормалью и
силовой линией вектора
напряженности E
company name
В
ФE м 2 В м
м
dФE E dS E dS n E dS cos En dS
En
- проекция вектора E на направление n

25.

Электростатическое поле и его характеристики
Вычисление потока вектора напряженности электрического поля
а) однородное поле, плоская поверхность:
б) общий случай:
ФE dФE E dS
company name
S
S
ФE E S E S cos
Поток может быть положительным и отрицательным в зависимости от
угла , величина которого определяется выбором направления нормали
n. Для расчета потока через замкнутую поверхность принято
использовать только внешнюю нормаль, т.е. нормаль, направленную
наружу от поверхности. Поэтому поток будет считаться отрицательным,
если линии напряженности поля направлены внутрь замкнутой
поверхности, и положительным, если линии направлены наружу.

26.

Электростатическое поле и его характеристики
Теорема Остроградского - Гаусса
Поток вектора напряженности электрического поля сквозь любую
замкнутую поверхность равен алгебраической сумме всех зарядов
внутри этой поверхности, деленной на 0 :
1 n
qi
S EndS 0
i 1
Поток
вектора
напряженности
электростатического поля через элементарную
площадку dS :
company name
dФ E dS E dS cos En dS
En E cos -
проекция вектора E на
нормаль n к площадке dS

27.

Электростатическое поле и его характеристики
Теорема Остроградского - Гаусса
Рассмотрим точечный заряд q.
Поверхность интегрирования – S, сфера
радиуса r, в любой точке поверхности
сферы E dS , E n E .
Напряженность поля точечного заряда :
q
E
4 0 r 2
Следовательно:
company name
q
q
q
2
E
dS
dS
dS
4
r
S n
S 4 0 r 2
4 0 r 2 S
4 0 r 2
S 4 r 2 - площадь
поверхности сферы
q
S EndS 0
- теорема
Остроградского - Гаусса

28.

Электростатическое поле и его характеристики
Применение теоремы Остроградского – Гаусса к расчету
электростатических полей
1) поле равномерно заряженной бесконечно протяженной плоскости
Поверхностная плотность заряда:
E к плоскости
dq
dS
Поверхность интегрирования – цилиндр,
перпендикулярный к плоскости.
S
S EndS бок EndS торцы
EndS 2ES 0
company name
0
E
2 0
Вектор напряженности не зависит от расстояния
до
плоскости.
Это
означает,
что
электростатическое поле бесконечной плоской
поверхности однородно.

29.

Электростатическое поле и его характеристики
Применение теоремы Остроградского – Гаусса к расчету
электростатических полей
2) поле равномерно заряженного бесконечно протяженного цилиндра
(нити)
dq Кл
Линейная плотность заряда:
dl м
Вектор напряженности перпендикулярен к нити и к
боковой поверхности цилиндра.
Поверхность интегрирования – цилиндр, радиус
цилиндра – r, длина – l, к боковой поверхности
цилиндра.
EndS EndS
S
бок
EndS ESбок E 2 rl
торцы
l
0
company name
0
S 2 rl - площадь боковой поверхности цилиндра
если r R , то
E
2 0 r
- напряженность поля на
поверхности заряженного
цилиндра

30.

Электростатическое поле и его характеристики
Применение теоремы Остроградского – Гаусса к расчету
электростатических полей
3) поле двух параллельных бесконечно протяженных плоскостей
Поверхностная плотность заряда:
E Силовые
dq
dS
линии поля «+» заряженной
плоскости показаны сплошными прямыми,
«-» заряженной – пунктирными.
полей обеих плоскостей
E Напряженности
равны по абсолютной величине:
E E
company name
E 0
E E E
E
0
E 0
2 0
Между плоскостями (область 2) оба вектора
имеют одинаковые
направления поэтому
результирующая напряженность численно
равна их сумме:
E E E 2
- поле сосредоточено между плоскостями, оно
однородно
2 0 0