Похожие презентации:
Электричество и магнетизм
1. ЭЛЕКТРИЧЕСТВО и МАГНЕТИЗМ
2. СПИСОК ЛИТЕРАТУРЫ:
СПИСОК ЛИТЕРАТУРЫ:
Курс общей физики [Текст]/И.В. Савельев.СПб.: Лань, 2011.
Общий курс физики [Текст]/Д.В. Сивухин.- М.:
Физматлит, 2008.
Курс физики: электричество [Текст]/Р.В.
Телеснин, В.Ф. Яковлев.- М.: Наука, 1970.
Электричество [Текст]/С.Г. Калашников.- М.:
Физматлит, 2008.
Сборник задач по общему курсу физики
[Текст]/В.С. Волькенштейн.- М.: Книжный мир,
2008.
Задачи по общей физике [Текст]/И.Е.
Иродов.- М.: Бином. Лаборатория знаний,
2012.
3.
Электричество и магнетизм
Электростатика
Постоянный электрический ток
Электромагнетизм
4. Электростатика – раздел физики, изучающий взаимодействие и свойства систем электрических зарядов неподвижных относительно выбранной ин
• Электростатика – раздел физики,изучающий взаимодействие и свойства
систем электрических зарядов
неподвижных относительно выбранной
инерциальной системы отсчета.
• Электрический заряд – мера
электрических свойств тел или их
составных частей.
Термин ввел Б.Франклин в 1749 г. Он же –
«батарея», «конденсатор», «проводник»,
«заряд», «разряд», «обмотка».
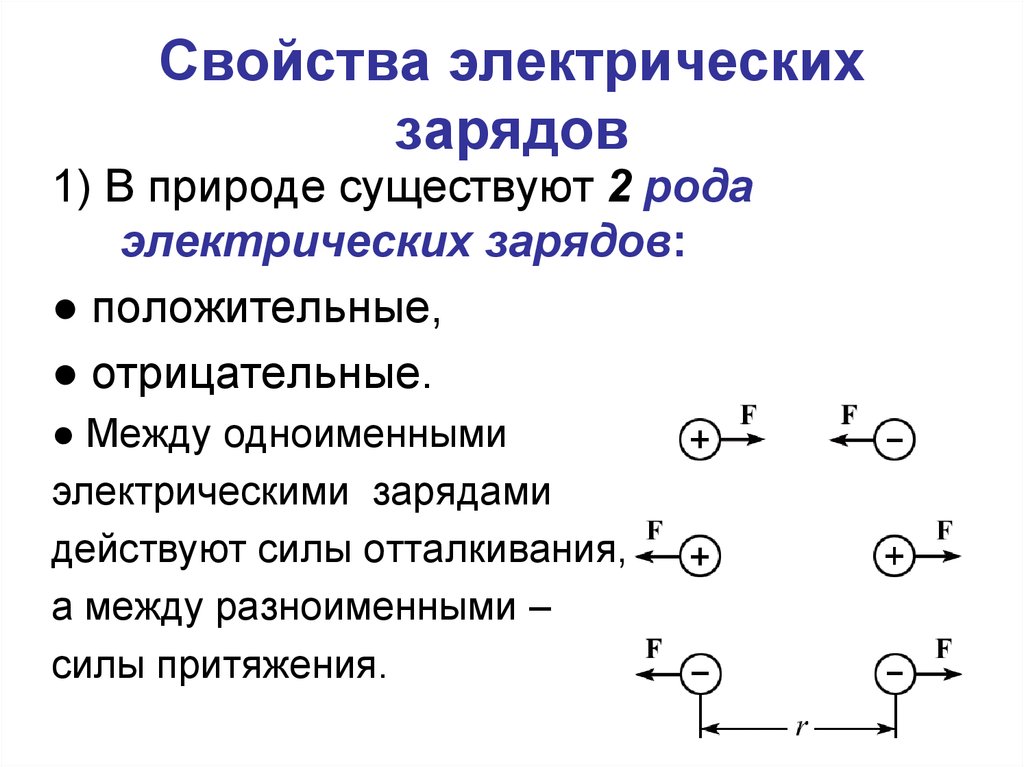
5. Свойства электрических зарядов
1) В природе существуют 2 родаэлектрических зарядов:
● положительные,
● отрицательные.
● Между одноименными
электрическими зарядами
действуют силы отталкивания,
а между разноименными –
силы притяжения.
6. Свойства электрических зарядов
2) Закон сохранения заряда –фундаментальный закон (экспериментально
подтвержден Фарадеем в 1845 г.)
Полный электрический заряд изолированной
системы есть величина постоянная.
Полный электрический заряд – сумма
положительных и отрицательных зарядов,
составляющих систему. q + q + q + … +q = const
1
2
3
n
7.
• В соответствии с законом сохранения зарядаразноименные заряды рождаются и исчезают
попарно: сколько родилось (исчезло)
положительных зарядов, столько родилось
(исчезло) отрицательных зарядов.
• Два элементарных заряда противоположных
знаков в соответствии с законом сохранения
заряда всегда рождаются и исчезают
одновременно.
Пример: электрон и позитрон, встречаясь друг
с другом, аннигилируют, рождая два или
более гамма-фотонов.
e – + e + 2g.
8. Свойства электрических зарядов
3) Электрический заряд – инвариант,его величина не зависит от выбора системы
отсчета.
4) Электрический заряд – величина
релятивистки инвариантная,
не зависит от того движется заряд или покоится.
5) Квантование заряда, электрический заряд
дискретен, его величина изменяется скачком.
Опыт Милликена (1910 – 1914 гг.)
q = n e, где n целое число. Заряд любого
тела составляет целое кратное от
элементарного электрического заряда
е = 1,6 10 19 Кл (Кулон).
9.
• Наименьшая частица, обладающаяотрицательным элементарным электрическим
зарядом, – электрон, me= 9,11·10-31 кг,
• Наименьшая частица, обладающая
положительным элементарным электрическим
зарядом, – позитрон.
• Таким же зарядом обладает протон, входящий
в состав ядра, mр= 1,67·10-27 кг.
10. Свойства электрических зарядов
6) Различные тела в классической физике взависимости от концентрации свободных
зарядов делятся на
● проводники (электрические заряды могут
перемещаться по всему их объему),
● диэлектрики (практически отсутствуют свободные
электрические заряды, содержит только связанные
заряды, входящие в состав атомов и молекул),
● полупроводники (по электропроводящим
свойствам занимают промежуточное положение
между проводниками и диэлектриками).
11. Свойства электрических зарядов
Проводники делятся на две группы:1) проводники первого рода (металлы), в
которых перенос зарядов (свободных электронов)
не сопровождается химическими превращениями,
2) проводники второго рода (растворы
солей, кислот), перенос зарядов (+ и − ионов)
в них сопровождается химическими изменениями.
12. Свойства электрических зарядов
7) Единица электрического заряда вСИ [1 Кл] – электрический заряд,
проходящий через поперечное
сечение проводника при силе тока 1 А
за время 1 с.
q = I·t.
13. Закон Кулона – основной закон электростатики
Описывает взаимодействие точечных зарядов.• Точечный заряд сосредоточен на теле,
линейные размеры которого пренебрежимо
малы по сравнению с расстоянием до других
заряженных тел.
Точечный заряд, как физическая модель, играет в
электростатике ту же роль, что и материальная точка
и абсолютно твердое тело в механике, идеальный газ
в молекулярной физике, равновесные процессы и
состояния в термодинамике.
14.
Закон КулонаУпругая
проволока
Стержень
Противовес
Стеклянная
палочка
Металлические
шарики
15. Закон Кулона
В 1785 г. Шарль Огюстен Кулонэкспериментальным путем с помощью
крутильных весов определил:
r
q1 q2
F k
,
2
r
сила взаимодействия F двух
неподвижных точечных
зарядов пропорциональна
величине каждого из зарядов
q1, q2 и обратно
пропорциональна квадрату
расстояния r между ними
k – коэффициент пропорциональности,
зависящий от выбранной системы единиц.
16. Закон Кулона
F• Сила
направлена по прямой,
соединяющей взаимодействующие заряды.
• Кулоновская сила является центральной
силой.
17. Закон Кулона в векторном виде
18. Закон Кулона
• Закон Кулона выполняется прирасстояниях
10-15 м < r < 4·104 км.
• В системе СИ: k =
1
4 0
H м2
2
Кл
= 9·109
[ м / Ф].
• В системе СГС: k = 1.
Кл 2
2
ε0 = 8,85·10-12
,[Ф / м] –
H м
электрическая постоянная.
19. Электрическое поле
• Согласно идее Фарадея электрическиезаряды не действуют друг на друга
непосредственно.
• Каждый из них создает в окружающим
пространстве электрическое поле.
• Поле одного заряда действует на другой
заряд и наоборот.
• По мере удаления от заряда поле
ослабевает.
20. Электрическое поле. Напряженность электрического поля
• Электрическое поле материально,оно существует независимо от нас и
наших знаний о нем.
• Главное свойство электрического
поля – действие его на электрические
заряды с некоторой силой.
• Электрическое поле неподвижных
зарядов называют
электростатическим. Оно не меняется
со временем.
21. Пробный точечный положительный заряд q0
• используют для обнаружения и исследованияэлектростатического поля.
• q0 не вызывает заметного
перераспределения зарядов на телах,
создающих поле.
• Силовая характеристика электростатического
поля определяет, с какой силой поле
действует на единичный положительный
точечный заряд q0. Такой характеристикой
является напряженность
электростатического поля.
22. Напряженность электрического поля – физическая величина, определяемая силой, действующей на пробный точечный положительный заряд q0, поме
Напряженность электрического поля –физическая величина, определяемая силой,
действующей на пробный точечный
положительный заряд q0, помещенный в
эту точку поля.
F
E
,
q0
q – источник
поля.
q0+ – пробный
заряд.
E Ex i E y j Ez k
E
2
Ex
2
Ey
2
Ez
23.
FE
.
q0
• Напряженность электростатического поля в
данной точке численно равна силе,
действующей на единичный положительный
точечный заряд, помещенный в данную точку
поля.
24.
• Зная напряженность поля в какой-либо точкепространства, можно найти силу,
действующую на заряд , помещенный в эту
точку:
F qE.
• Это другой вид закона Кулона, который и
вводит понятие электрического поля,
создающееся зарядами во всем окружающем
пространстве,
а также представляет закон действия данного
поля на любой заряд.
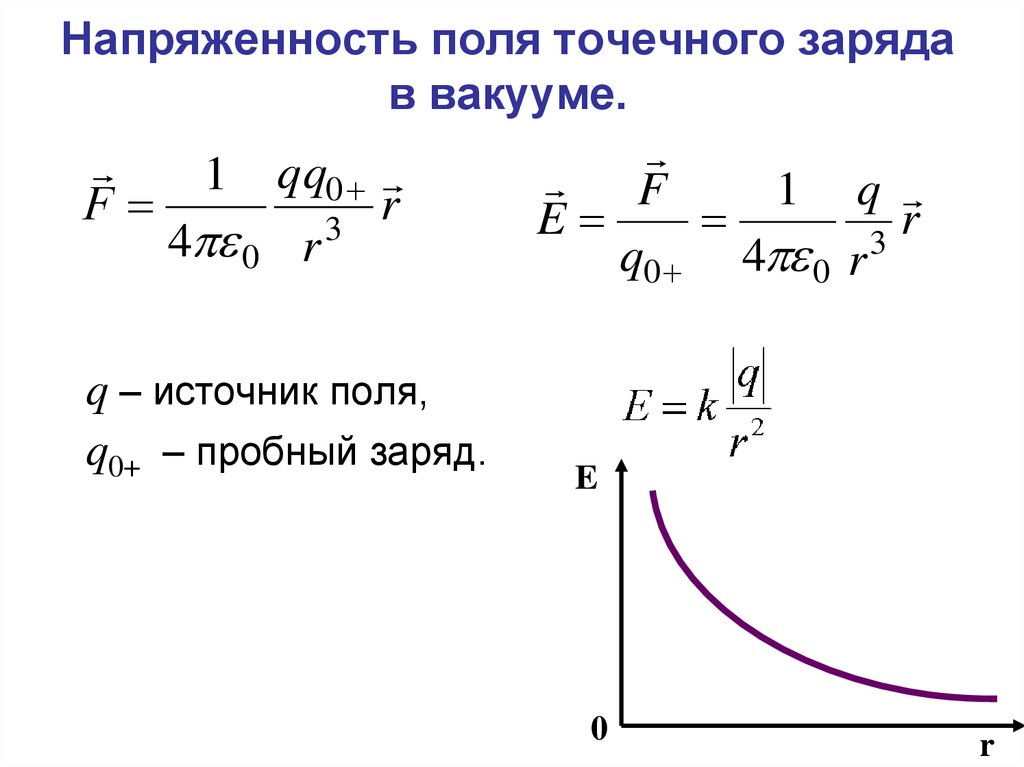
25. Напряженность поля точечного заряда в вакууме.
1 qq0F
1 q
F
r
E
r
3
3
4 0 r
q0 4 0 r
q – источник поля,
q0+ – пробный заряд.
E
0
r
26. Напряженность электрического поля
• E совпадает снаправлением силы F,
действующей на пробный
заряд q0+ .
• Поле создается
положительным зарядом –
вектор напряженности
электрического поля E
направлен от заряда.
27. Напряженность электрического поля
• СИ: E измеряется в [1 Н /Кл = 1 В/м] –это напряженность такого поля, которое
на точечный заряд 1 Кл действует с
силой 1 Н.
28. Принцип суперпозиции напряженности электрического поля
• Опытно установлено, что взаимодействиедвух зарядов не зависит от присутствия
других зарядов.
• В соответствии с принципом независимости
действия сил: на пробный заряд,
помещенный в некоторую точку, будет
действовать сила F со стороны всех зарядов
qi, равная векторной сумме сил Fi,
действующих на него со стороны каждого из
зарядов.
n
F F1 F2 ... Fn Fi
i 1
29. Принцип суперпозиции напряженности электрического поля
F q0 EFi q0 Ei
n
q0 E q0 Ei ,
i 1
n
E Ei
i 1
Напряженность электростатического поля,
создаваемого системой точечных зарядов
в данной точке, равна геометрической сумме
напряженностей полей, создаваемых в этой
точке каждым из зарядов в отдельности.
30. Поле электрического диполя
• Электрический диполь - система двуходинаковых по величине разноименных
точечных зарядов, расстояние l между
которыми значительно меньше расстояния
до тех точек, в которых определяется поле.
• Ось диполя прямая, проходящая через оба
заряда.
l – плечо диполя – вектор,
r
pl
-q
l
+ q
проведенный от отрицательного
заряда к положительному.
Дипольный
мом
pl ql
31. Поле электрического диполя
>>l
→
Диполь
можно
рассматриват
Молекула воды
Н2О систему
ь как
обладает дипольным
2-х
точечных
моментом р =зарядов.
6,3 10 30 Кл м.
Вектор дипольного
момента направлен от
центра иона кислорода О2
к середине прямой,
соединяющей центры
r
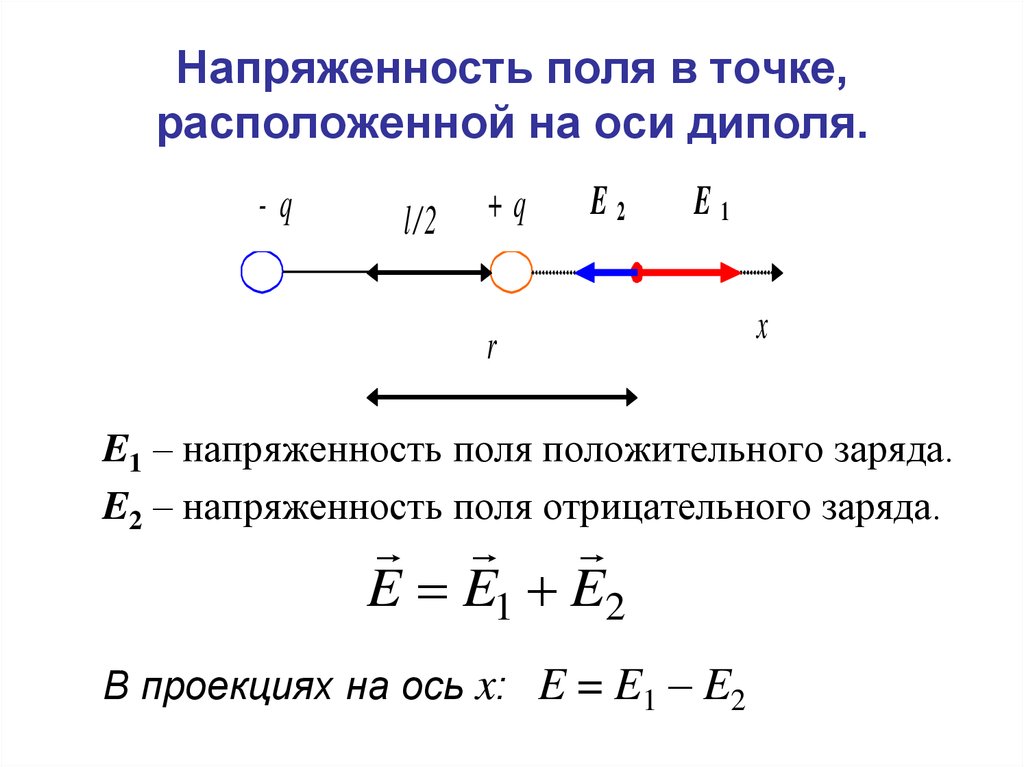
32. Напряженность поля в точке, расположенной на оси диполя.
-ql/2
+q
E2
E1
r
x
E1 – напряженность поля положительного заряда.
E2 – напряженность поля отрицательного заряда.
E E1 E2
В проекциях на ось x: E = E1 – E2
33. Напряженность поля в точке, расположенной на оси диполя.
-ql/2
+q
E2
E1
r
x
l
l
(r ) 2 (r ) 2
1
q
1
q
q
2
2
E
4 0 (r l ) 2 4 0 (r l ) 2 4 0 (r l ) 2 (r l ) 2
2
2
2 2
l
r l ( r ) r ,
2
q
2rl
2ql
.
4
3
4 0 r
4 0 r
E
2 pl
4 0 r
l
( r ) r .
2
3
34. Напряженность поля в точке, расположенной на оси диполя.
2 plE
.
3
4 0 r
• Поле диполя убывает быстрее в
зависимости от расстояния по
сравнению с полем точечного заряда.
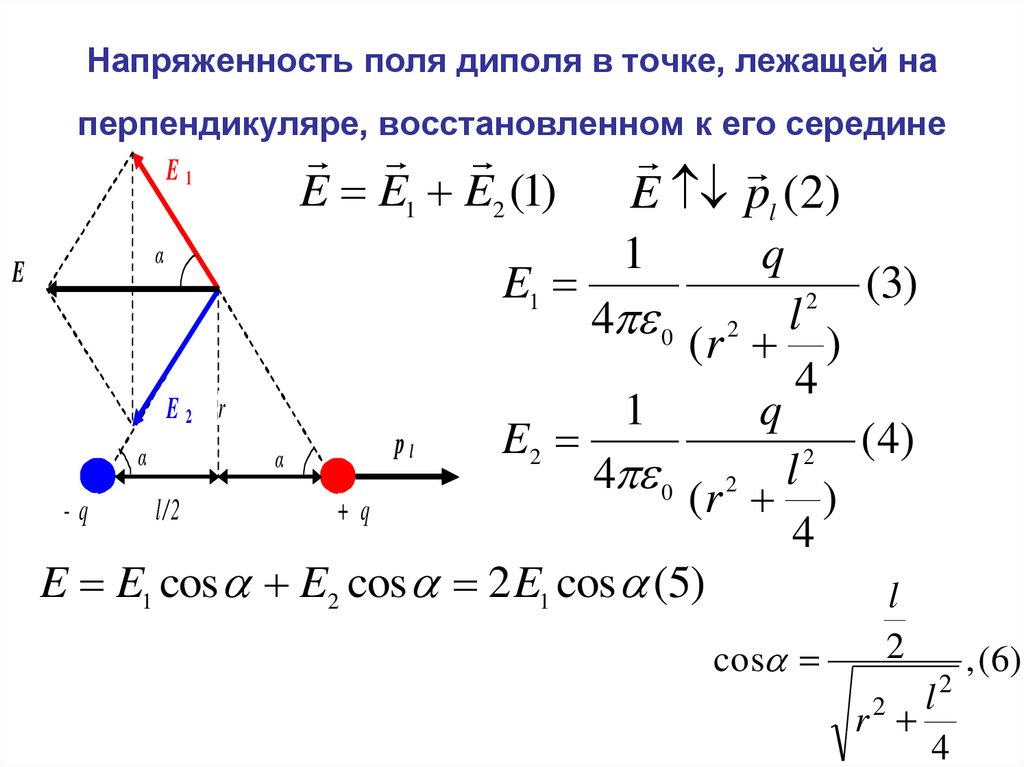
35. Напряженность поля диполя в точке, лежащей на перпендикуляре, восстановленном к его середине
E pl (2)1
q
E1
(3)
2
4 0 2 l
(r )
4
E E1 E2 (1)
E1
α
E
E2 r
α
α
pl
E2
1
4 0
q
2
l
(r )
-q
l/2
+q
4
E E1 cos E2 cos 2 E1 cos (5)
( 4)
2
cos
l
2
2
l
r2
4
, ( 6)
36. Напряженность поля диполя в точке, лежащей на перпендикуляре, восстановленном к его середине
Уравнения (3),(4), (6)→(5):E 2
1
q
4 0
2
l
2
(r )
4
l
2
l
2 r
4
l2
r l 0
4
2
ql
4 0 r 3
E pl
pl ql
E1
α
E
E2 r
α
-q
pl
α
l/2
+q
E
pl
4 0 r
3
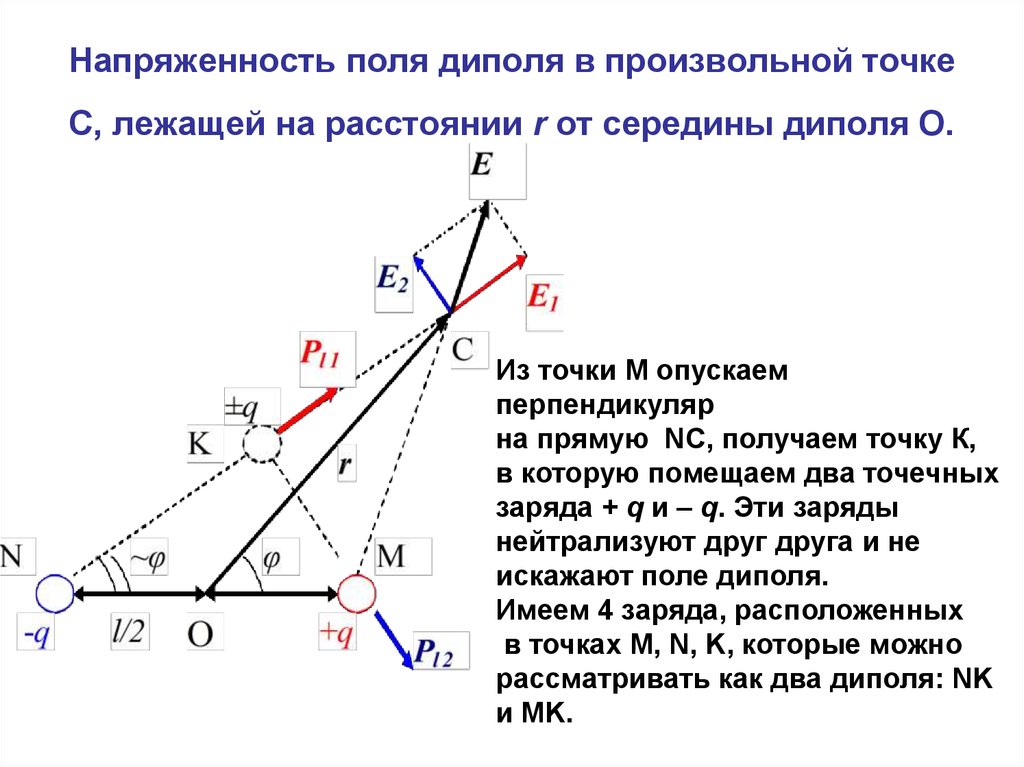
37. Напряженность поля диполя в произвольной точке С, лежащей на расстоянии r от середины диполя О.
Из точки М опускаемперпендикуляр
на прямую NC, получаем точку К,
в которую помещаем два точечных
заряда + q и – q. Эти заряды
нейтрализуют друг друга и не
искажают поле диполя.
Имеем 4 заряда, расположенных
в точках M, N, K, которые можно
рассматривать как два диполя: NK
и MK.
38. Напряженность поля диполя в произвольной точке С, лежащей на расстоянии r от середины диполя О.
l << r →Угол СNM ≈ φ→• Электрический момент
диполя NK:
pl1 q NK ql cos pl cos (1)
• Электрический момент
диполя MK:
pl 2 q KM ql sin pl sin (2)
pl1 pl 2
39.
Для диполя NK точка Слежит на его оси
1 2 pl1
E1
3 (3)
4 0 r
Для диполя МК точка С
лежит на перпендикуляре
1 pl 2
E2
3 (4)
4 0 r
E1 E2
pl1 pl 2
E
2
E1
2
E2
1
1
4 0 r
3
(2 pl1 ) pl 2
2
2
40.
Уравнения (1), (2) → (5):E
1
4 0 r
pl
4 0 r
2
2
4
cos
sin
3
pl
4 0 r
2
2
2
2
4
p
cos
p
sin
l
l
3
3 cos 1
2
3
41.
В предельных случаях:а) если , 0 0 то есть точка лежит на
оси диполя, то получим
2 pl
E
.
3
4 0 r
б) если , 90
то есть точка лежит на
перпендикуляре к оси диполя, то
получим
0
E
pl
4 0 r
3
.
42. Линейная, поверхностная и объемная плотности зарядов
• Хотя электрический заряд дискретен,число его носителей в
макроскопических телах столь велико,
что можно ввести понятие плотности
заряда, использовав представление о
непрерывном «размазанном»
распределении заряда в пространстве.
43.
• Линейнаяплотность заряда:
dq Кл
,
dl м
заряд, приходящийся на единицу длины.
• Поверхностная
плотность заряда:
заряд, приходящийся на единицу
площади.
• Объемная
плотность заряда:
заряд, приходящийся на единицу
объема.
dq Кл
, 2
dS м
dq Кл
, 3
dV м
44. Линейная, поверхностная и объемная плотности зарядов
Полеdq dl
dq dS
dq dV
dE k
dE k
dE k
dl
r
2
l
dS
r
E k
dl
2
S
dV
r
E k
2
E k
V
r2
dS
r2
dV
r2
45. Силовые линии напряженности электрического поля - линии, касательные к которым в каждой точке совпадают с вектором Е
• По их направлению можносудить, где расположены
положительные (+) и
отрицательные (–) заряды,
создающие электрическое
поле.
• Густота линий
(количество линий, пронизывающих единичную
площадку поверхности, перпендикулярную к
ним) численно равно модулю вектора Е.
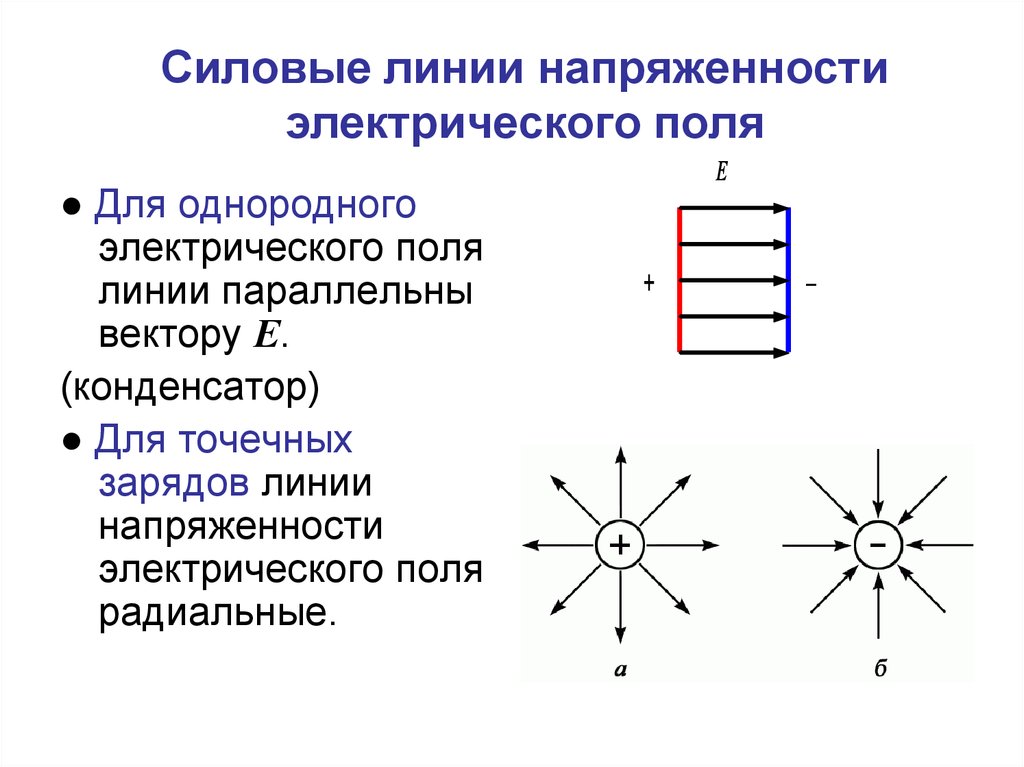
46. Силовые линии напряженности электрического поля
● Для однородногоэлектрического поля
линии параллельны
вектору Е.
(конденсатор)
● Для точечных
зарядов линии
напряженности
электрического поля
радиальные.
Е
+
–
47. Силовые линии напряженности электрического поля
• Силовые линии напряженностиэлектрического поля не замкнуты, имеют
начало и конец. →
Можно говорить, что электрическое поле имеет
«источники» и «стоки» силовых линий.
• Силовые линии начинаются
на положительных (+)
зарядах (Рис. а), заканчиваются
на отрицательных (–) зарядах (Рис. б).
• Силовые линии не пересекаются.
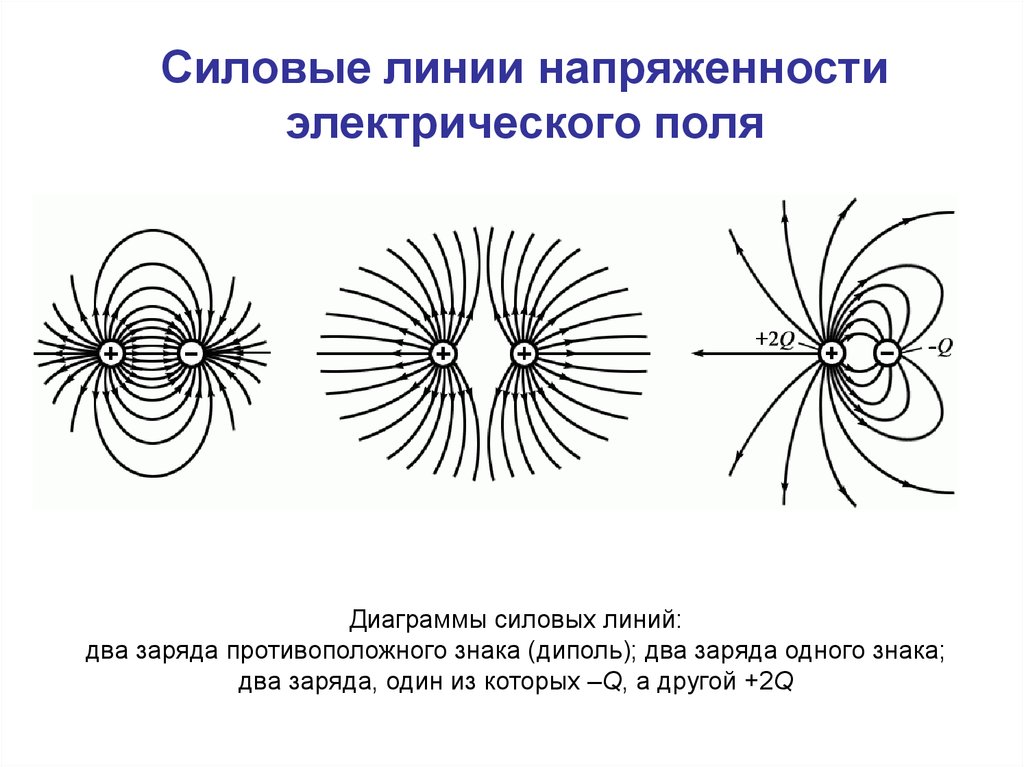
48. Силовые линии напряженности электрического поля
Диаграммы силовых линий:два заряда противоположного знака (диполь); два заряда одного знака;
два заряда, один из которых –Q, а другой +2Q
49.
Величина напряженности электрического поляхарактеризуется густотой линий.
● Число линий
N, пронизывающих
единичную
dS E ,
n
N E;
nE 0
где
- вектор положительной нормали к dS.
● Если единичная площадка dS не
перпендикулярна вектору Е, то
nE ;
число линий N EdS cos En dS , где En E cos .
50. Поток вектора напряженности электрического поля
● Произвольная площадка dS.Поток вектора напряженности
электрического поля через
площадку dS:
dФ
E
dS
E
d
S
E
n
В м
dS dS n - псевдовектор, модуль
которого равен dS, а направление совпадает
с направление вектора n к площадке dS.
Е = const
→
dФЕ = N - числу линий
вектора напряженности электрического поля
Е, пронизывающих площадку dS.
51. Поток вектора напряженности электрического поля
● Произвольная замкнутая поверхностьS.ФЕ dФE En dS
S
S
Положительное направление вектора n
- внешняя нормаль, т.е. направленная
наружу области, охватываемой
поверхностью S.
52. Поток вектора напряженности электрического поля
• Если поверхность не плоская, а поленеоднородное, то выделяют малый элемент
dS, который считать плоским, а поле –
однородным.
Поток вектора напряженности электрического
поля:
Ф EdS
Е
S
Знак потока совпадает со знаком заряда.
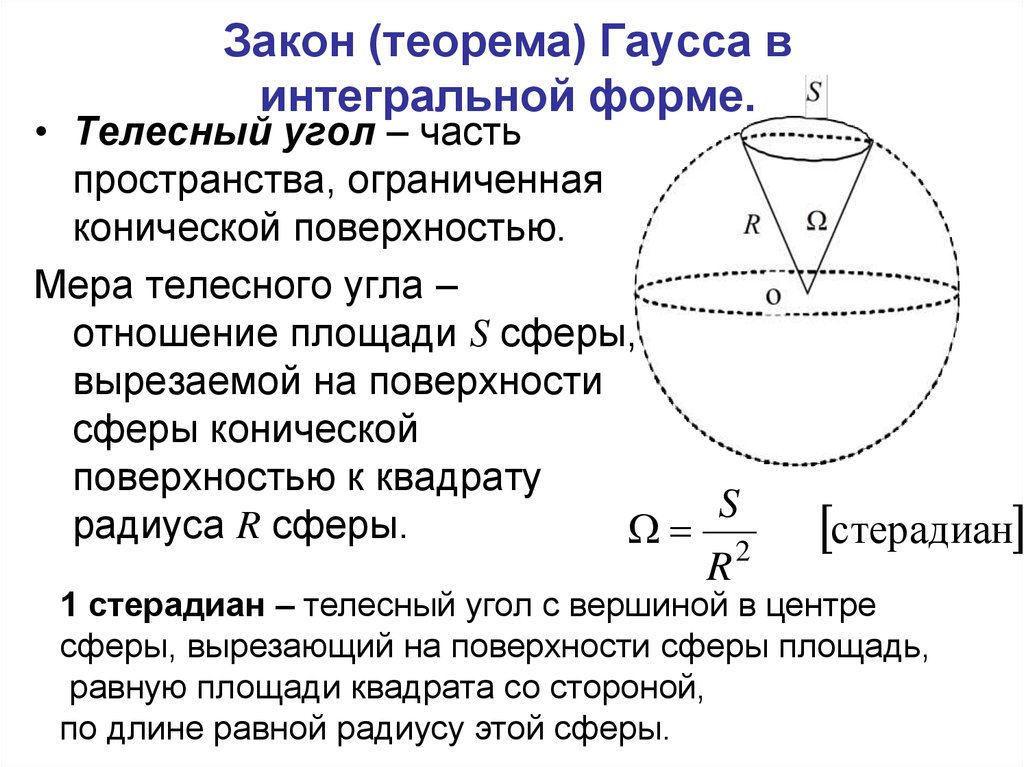
53. Закон (теорема) Гаусса в интегральной форме.
• Телесный угол – частьпространства, ограниченная
конической поверхностью.
Мера телесного угла –
отношение площади S сферы,
вырезаемой на поверхности
сферы конической
поверхностью к квадрату
S
радиуса R сферы.
2
R
стерадиан
1 стерадиан – телесный угол с вершиной в центре
сферы, вырезающий на поверхности сферы площадь,
равную площади квадрата со стороной,
по длине равной радиусу этой сферы.
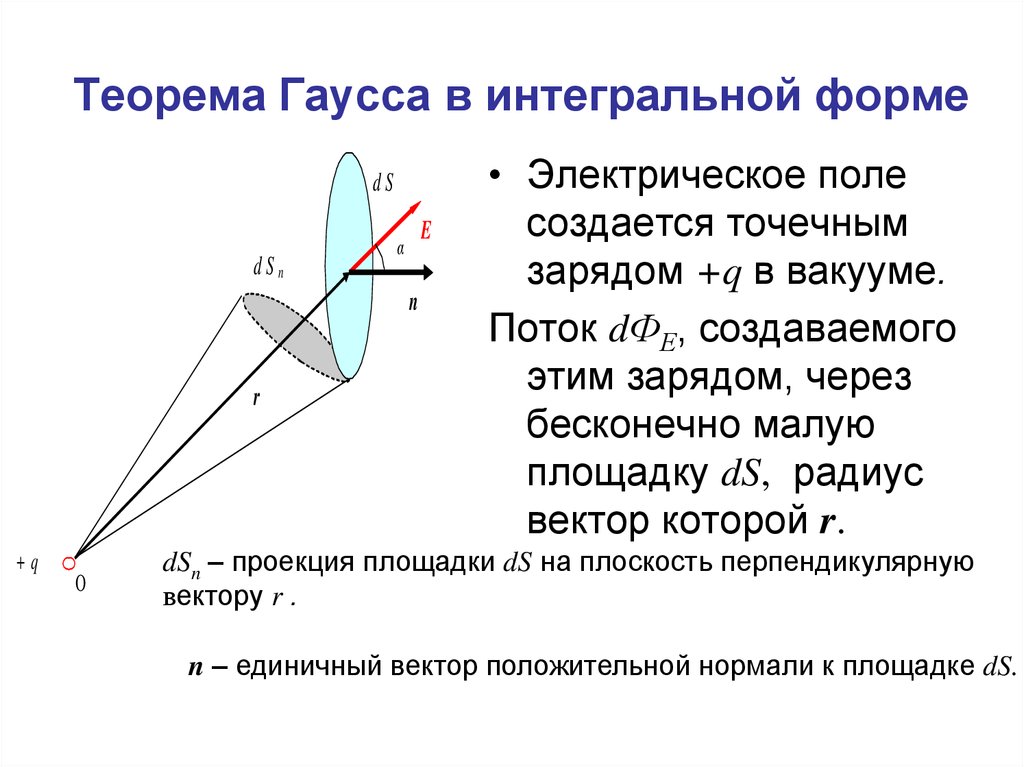
54. Теорема Гаусса в интегральной форме
dSdSn
E
α
n
r
+q
O
• Электрическое поле
создается точечным
зарядом +q в вакууме.
Поток dФЕ, создаваемого
этим зарядом, через
бесконечно малую
площадку dS, радиус
вектор которой r.
dSn – проекция площадки dS на плоскость перпендикулярную
вектору r .
n – единичный вектор положительной нормали к площадке dS.
55. Теорема Гаусса в интегральной форме
Начало отсчета совмещаем с точечным зарядом +q.dS
E
α
dSn
n
ФЕ E dS
E
qr
4 0 r
3
dS dS n
r
(1)
(2)
(3)
qr
+q
O
qdSn
qrdS
(4)
dФЕ
dS
cos( r , dS )
3
3
2
4 0 r
4 0 r
4 0 r
dS cos( r , dS ) dS cos dS n (5)
56. Теорема Гаусса в интегральной форме
dSdSn
E
α
n
r
Поток dФЕ через площадку dS и dSn
один и тот же.
Площадка dSn совпадает с элементом
шаровой поверхности радиуса R с
центром в точке О.
α - мал,
R ≈ r.
d
+q
O
dSn
dSn r d , (6)
2
r2
qdSn
dФЕ
, (4)
2
4 0 r
qdSn
qr d
q
dФЕ
d .(7)
2
2
4 0 r
4 0 r
4 0
2
57. Теорема Гаусса в интегральной форме
• Для конической поверхности:q
ФЕ dФЕ
d
.(8)
4 0
0 4 0
• Для замкнутой поверхности:
ФЕ EdSn
S
S
q
4 0 r
2
q
dSn
q
4 0 r
4 r
2
2
q
0
Или из уравнения (8):
ФЕ dФЕ
S
4
q
q
q
4 d 4 4
0
0
0
0
58. Теорема Гаусса в интегральной форме
● Точечный заряд +q охваченсферической поверхностью.
ФЕ
q
0
● Этот результат справедлив
для замкнутой поверхности
любой формы, так как
каждая линия вектора E,
пронизывающая сферу,
пройдет и сквозь эту
поверхность.
59.
• Если произвольная поверхность окружает k–зарядов, то согласно
принципу
суперпозиции:
E E1 E2 ... Ek
k
k
ФЕ En dS ( Eni ) dS Eni
S
S
i 1
i 1 S
q
dS
i
0
Теорема Гаусса: для электрического поля в
вакууме поток вектора напряженности
электрического поля сквозь произвольную
замкнутую поверхность равен
алгебраической сумме заключенных внутри
этой поверхности зарядов, деленных на ε0.
60. Теорема Гаусса в интегральной форме
• Если внутри поверхности имеется каким-тообразом распределенный заряд с объемной
плотностью ρ ( ρ = dq/dV, Кл/м3), то
суммарный заряд, заключенный внутри
поверхности площадью S, охватывающей
объем V:
qi dV
i
V
ФE
1
dV
0 V
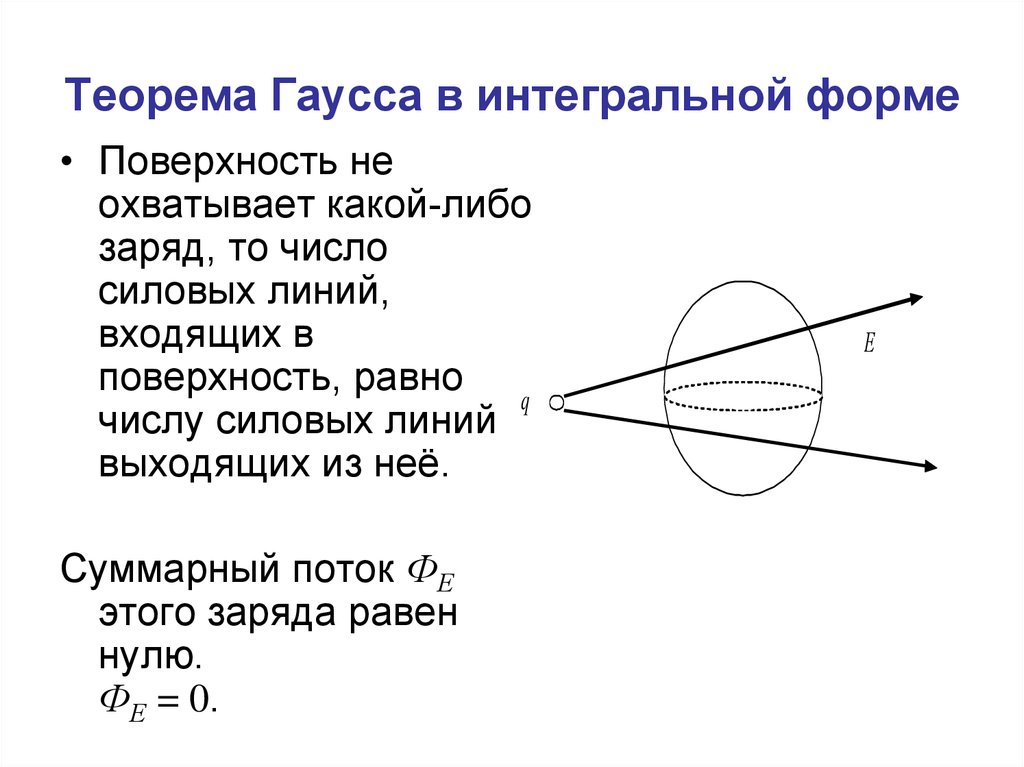
61. Теорема Гаусса в интегральной форме
• Поверхность неохватывает какой-либо
заряд, то число
силовых линий,
входящих в
поверхность, равно q
числу силовых линий
выходящих из неё.
Суммарный поток ФЕ
этого заряда равен
нулю.
ФЕ = 0.
Е
62. Методика применения теоремы Гаусса для расчета электрических полей – второй способ определения напряженности электрического поля Е
• Теорема Гаусса применяется длянахождения полей, созданных телами,
обладающими геометрической
симметрией. Тогда векторное
уравнение сводится к скалярному.
63. Методика применения теоремы Гаусса для расчета электрических полей – второй способ определения напряженности электрического поля Е
1) Находится поток ФЕ вектора Е поопределению потока.
Ф Е Ed S
S
2) Находится поток ФЕ
по теореме Гаусса.
ФЕ
qi
0
3) Из условия равенства потоков находится
вектор Е.
qi 1
ФЕ EdS
dV
S
0
0 V
E Exi E y j Ez k .
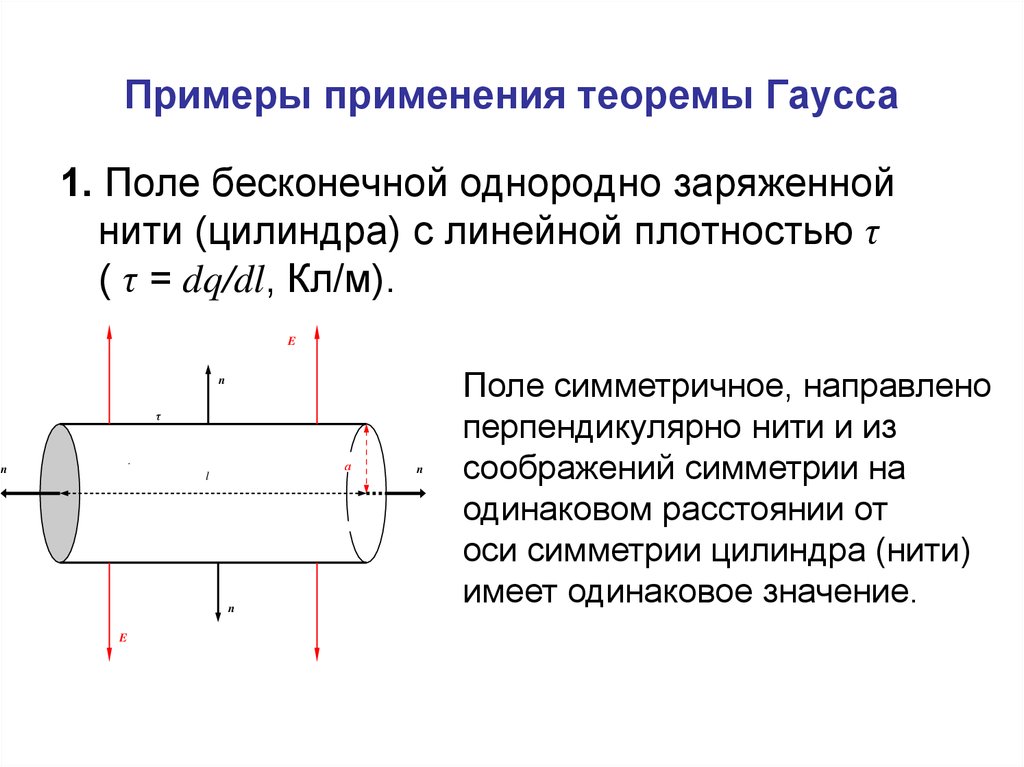
64. Примеры применения теоремы Гаусса
1. Поле бесконечной однородно заряженнойнити (цилиндра) с линейной плотностью τ
( τ = dq/dl, Кл/м).
E
n
τ
n
а
l
n
E
n
Поле симметричное, направлено
перпендикулярно нити и из
соображений симметрии на
одинаковом расстоянии от
оси симметрии цилиндра (нити)
имеет одинаковое значение.
65. 1. Поле бесконечной заряженной нити
Ф Е EdS 2 EdS EdSПоток вектора Е:
• Основание цилиндра:
E , n
2
S
S осн
ФЕосн 2 EdS cos( E , n ) 0.(2)
S осн
• Боковая поверхность:
E, n 0
E
cos( E, n) 1
n
τ
n
а
l
n
E
S бок
n
66. 1. Поле бесконечной заряженной нити
ФЕ ФЕ осн ФЕбок1)
0 EdS cos( E , n ) EdS
S бок
S бок
E dS E 2 al
S бок
2)
3)
ФЕ
qi
0
dl l
l
l
E 2 al
0
0
0
E
2 0 a
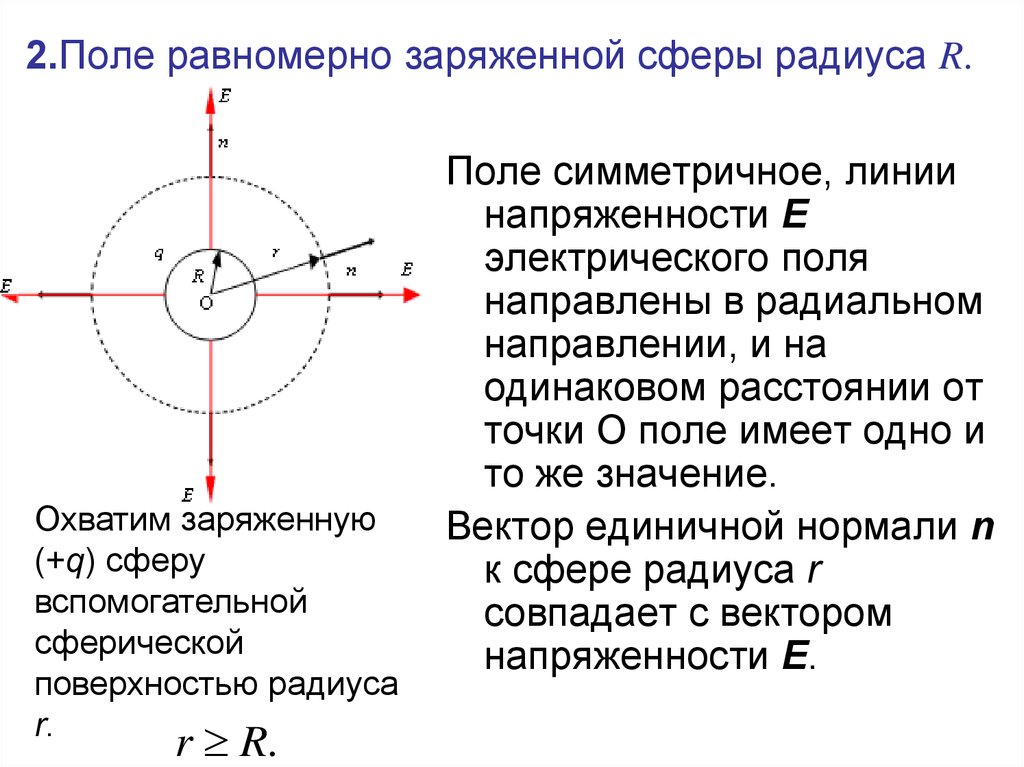
67. 2.Поле равномерно заряженной сферы радиуса R.
Охватим заряженную(+q) сферу
вспомогательной
сферической
поверхностью радиуса
r.
r R.
Поле симметричное, линии
напряженности Е
электрического поля
направлены в радиальном
направлении, и на
одинаковом расстоянии от
точки О поле имеет одно и
то же значение.
Вектор единичной нормали n
к сфере радиуса r
совпадает с вектором
напряженности Е.
68. 2.Поле равномерно заряженной сферы радиуса R.
1) ФЕ EdS EdS cos( E , dS )S
S бок
E dS E 4 r 2
S
3)
ФЕ E 4 r
2
2)
ФЕ
q
0
qi
0
q
0
E
q
4 0 r
2
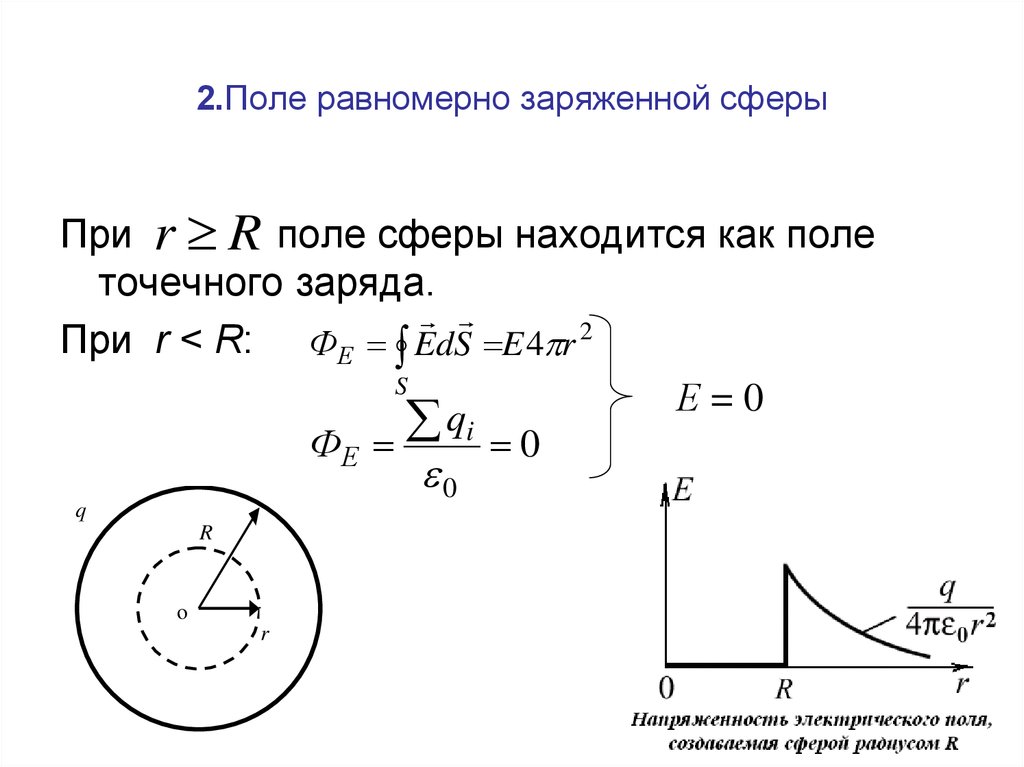
69. 2.Поле равномерно заряженной сферы
При r R поле сферы находится как полеточечного заряда.
При r < R: ФЕ EdS E 4 r 2
S
Е=0
q
i
ФЕ
0
0
q
R
o
r
70. 3. Поле равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда + σ
3. Поле равномерно заряженной бесконечнойплоскости с поверхностной плотностью заряда + σ
( σ = dq/dS, Кл/м2).
Поле симметричное,
вектор Е
перпендикулярен
плоскости с
поверхностной
плотностью заряда +σ
и на одинаковом
В качестве замкнутой поверхности расстоянии от
возьмем цилиндр, основания
плоскости имеет
которого параллельны плоскости,
одинаковое значение.
и который делится заряженной
Е
S
с
Е
с
с
с S
+σ
плоскостью на две равные половины.
71. 3. Поле равномерно заряженной бесконечной плоскости
ФЕ ФЕ осн ФЕбок 2 EdS EdSS осн
S бок
2 ESосн 0( Е dS ) 2 ES
ФЕ
q
i
0
S
2 ES
0
S
;
0
Е
E
2 0
S
с
с
с
с S
+σ
Е
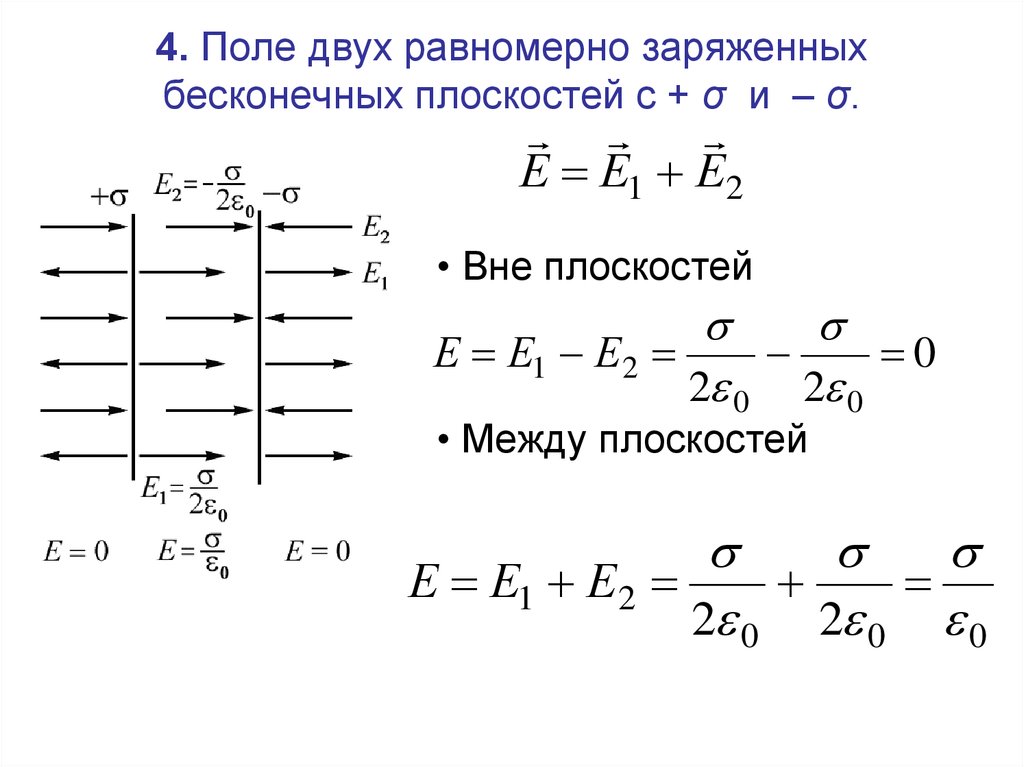
72. 4. Поле двух равномерно заряженных бесконечных плоскостей с + σ и – σ.
4. Поле двух равномерно заряженныхбесконечных плоскостей с + σ и – σ.
Е Е1 Е2
• Вне плоскостей
Е Е1 Е2
0
2 0 2 0
• Между плоскостей
Е Е1 Е2
2 0 2 0 0


























































 Физика
Физика








