Призма. Площадь поверхности призмы. Определение призмы

1. Призма. Площадь поверхности призмы

2.

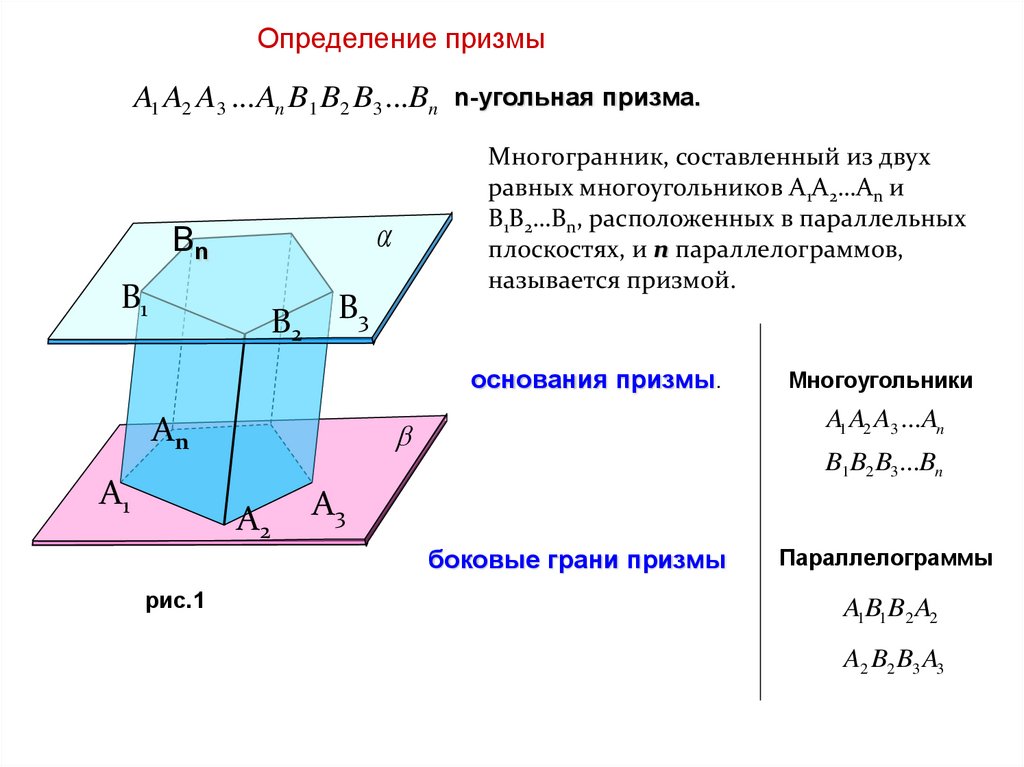
Определение призмы
A1 A2 A3 ... An B1 B2 B3 ...Bn n-угольная призма.
Многогранник, составленный из двух
равных многоугольников А1А2…Аn и
В1В2…Вn, расположенных в параллельных
плоскостях, и n параллелограммов,
называется призмой.
Bn
B1
B2
B3
основания призмы.
Аn
А1
A1 A2 A3 ...An
А2
B1B2 B3...Bn
А3
боковые грани призмы
рис.1
Многоугольники
Параллелограммы
A1B1B2 A2
A2 B2 B3 A3

3.

1. Среди изображенных тел выберите те, которые являются призмами.
1
2
3
4
5
Призмами являются многогранники под номерами 1 и 6
6

4.

2. Назовите для призмы:
B1
Вершины
C1
Боковые ребра
точки: A B C D
A1 B1 C1 D1
отрезки DD1 CC1
D1
A1
BB1 AA1
Боковые грани
параллелограммы
ABB1A1
B
C
CDD1C1 ADD1A1
Основания
A
BCC 1B1
D
Противоположные грани
Диагонали граней
Диагонали призмы
многоугольники
ABCD A1B1C1D1
ABB1A1
CDD1C1
отрезки C1D
CB1
отрезки BD1
AC1

5.

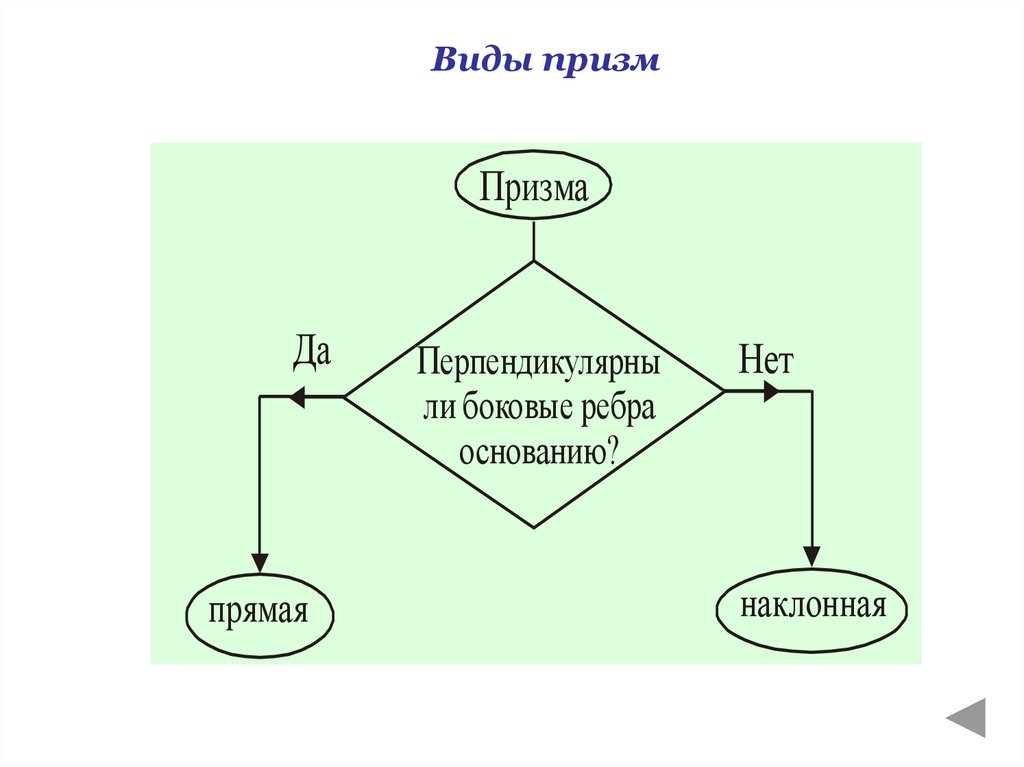
Виды призм
Призма
Да
прямая
Перпендикулярны
ли боковые ребра
основанию?
Нет
наклонная

6. Прямые призмы

7. Наклонные призмы

Треугольная наклонная
призма
Четырехугольная наклонная
призма

8.

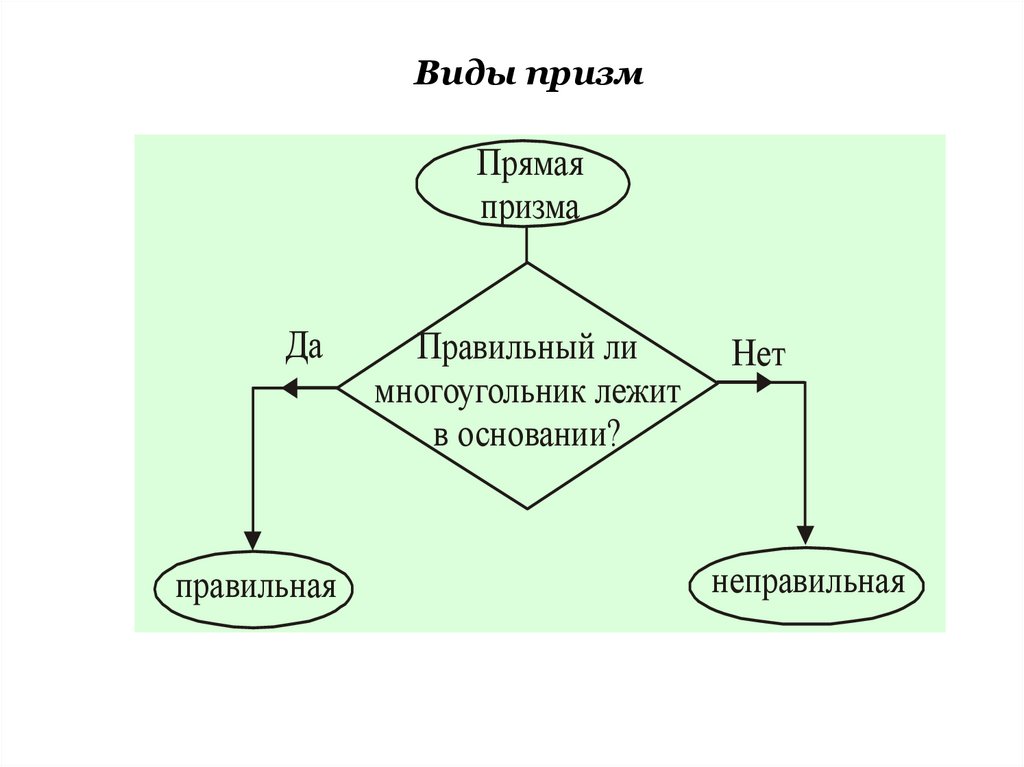
Виды призм
Прямая
призма
Да
правильная
Правильный ли
многоугольник лежит
в основании?
Нет
неправильная

9. Площадь поверхности призмы

10.

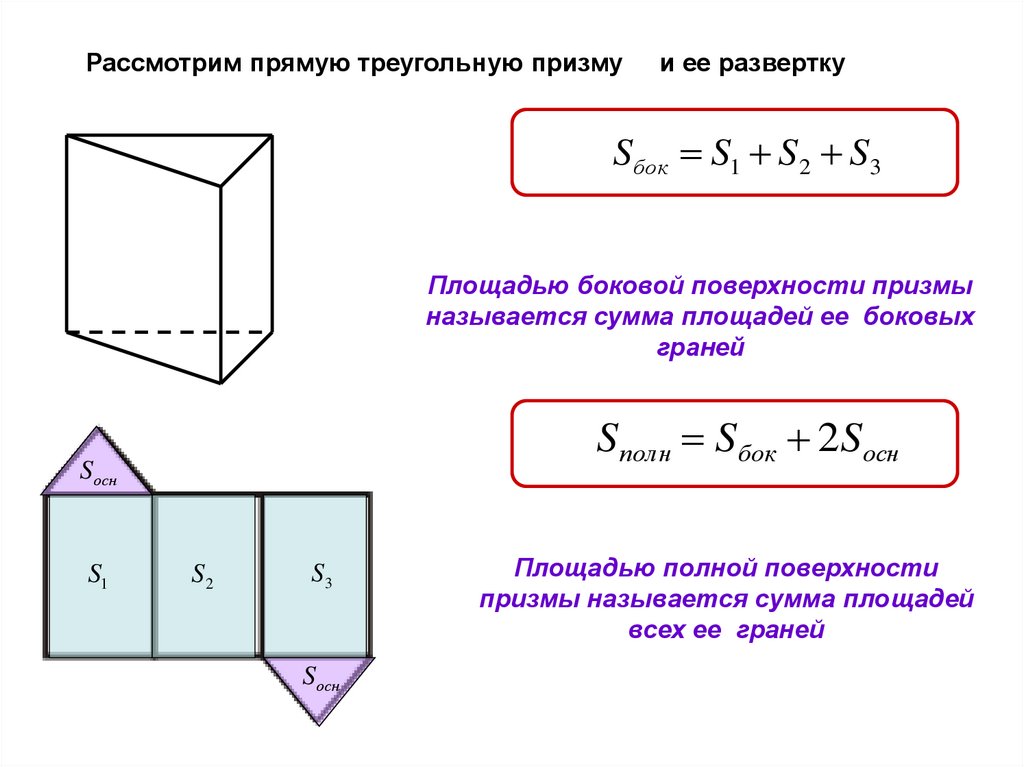
Рассмотрим прямую треугольную призму
и ее развертку
Sбок S1 S2 S3
Площадью боковой поверхности призмы
называется сумма площадей ее боковых
граней
S полн Sбок 2Sосн
S осн
S1
S2
S3
S осн
Площадью полной поверхности
призмы называется сумма площадей
всех ее граней

11.

Рассмотрим прямую шестиугольную призму
и ее развертку
S полн S бок 2 S осн
h
Pocн
S бок Росн h

12. Задача № 229(а)

C1
A1
A
C
10
AB =10 см.
AA1 =15 см.
Найти: S бок , S полн
B1
15
Дано: ABCA1 B1C1 правильная треугольная призма.
Решение
S бок Росн h
S полн S бок 2 S осн
B
1) Так как призма правильная, то в ее основании лежит
правильный треугольник , значит АВ = ВС = АС = 10 см
и A B C 60 0
2) Тогда периметр основания Р = 10·3=30 см. Sбок=30·15=450 см2
3) Площадь основания найдем по формуле
1
3
S осн 10 10 sin 600 50
25 3
2
2
Ответ:
450 50 3
S осн
1
AB BC sin B
2
Sполн Sбок 2Sосн 450 2 25 3 450 50 3

13.

Задача. Сторона основания правильной треугольной призмы равна
6см., а диагональ боковой грани равна 10см. Найти площадь боковой и
полной поверхности призмы.
A1 Дано: ABCA B C правильная треугольная призма.
1 1 1
C1
AB = 6 см.
B1
10
BC 1 = 10 см.
Найти: S бок , S полн
Решение
A
C
6
B
1) Так как призма правильная, то в ее основании лежит
правильный треугольник , значит АВ = ВС = АС = 6 см и
A B C 60 0
2) Найдем периметр основания и его площадь: Pосн 6 3 18
1
1
3
S осн AB BC sin B 6 6 sin B 18
9 3
2
2
2
3) Для нахождения высоты призмы. рассмотрим BCC1
4) По условию призма прямая, значит CC1 ABC , CB ABC CC1 CB
В BCC1 по т. Пифагора находим CC1 8
Sполн Sбок 2Sосн 18 8 2 9 3 144 18 3
Ответ: 144 18 3