Таблица истинности для операции эквивалентности

1.

2. ВСПОМНИМ ПРОШЛЫЙ УРОК

• Как выглядит таблица истинности для
операции ЭКВИВАЛЕНТНОСТИ?
• С помощью какой связки слов
составляется высказывание –
эквивалентность?
• Приведите пример истинного и ложного
высказывания – эквивалентности.

3. ВСПОМНИМ ПРОШЛЫЙ УРОК

• Как выглядит таблица истинности для
операции ИМПЛИКАЦИЯ?
• С помощью какой связки слов
составляется высказывание –
импликация?
• Приведите пример истинного и ложного
высказывания – импликации.

4. ВСПОМНИМ ПРОШЛЫЙ УРОК

Определите истинность формул:
1)
2)
3)
4)
5)
6)
1 => 0
0 => 0
1 => 1
0 <=> 1
0 <=> 0
(1 ^ 0) => 0
7) (1 ^ 1) =>1
8) (0 ^ 1) => (1 ^ 0)
9) (0 ^ ¬1) <=> 0
10)(¬1 ν 0) => 1
11)(0 ν ¬0) <=> (1 ν ¬1)
12)(1 ^ 1 ν 0) <=> 0

5. Проверим домашнюю задачу

Что можно сказать об истинности формулы?

6. тавтология

всегда истинное выражение
Например, докажем, что
(X ^ Y) → (X v Y)
является тавтологией

7. тавтология

всегда истинное выражение
Некоторые тавтологии являются
логическими законами.

8. Закон тождества

Всякое высказывание тождественно
самому себе
A A

9. Закон непротиворечия

Высказывание не может быть одновременно
истинным и ложным. Если высказывание А —
истинно, то его отрицание не А должно быть
ложным. Следовательно, логическое
произведение высказывания и его отрицания
должно быть ложно
A A 0

10. Закон исключенного третьего

Высказывание может быть либо истинным,
либо ложным, третьего не дано. Это
означает, что результат логического
сложения высказывания и его отрицания
всегда принимает значение истина
A A 1

11. Закон двойного отрицания

Если дважды отрицать некоторое
высказывание, то в результате мы
получим исходное высказывание
A A

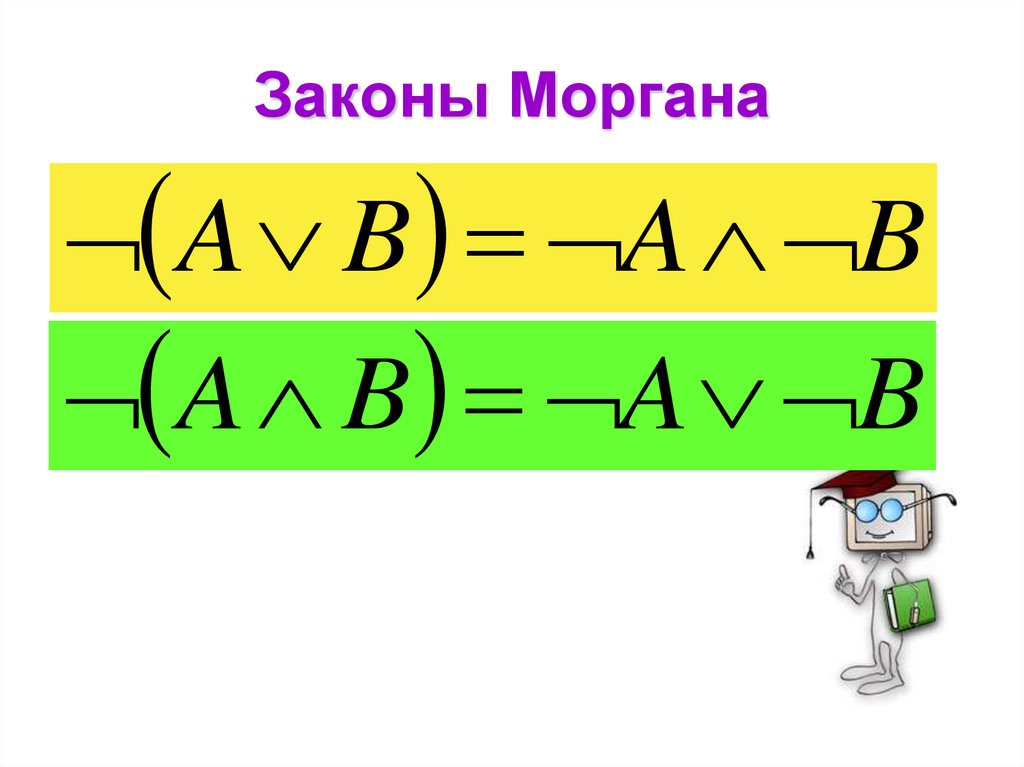
12. Законы Моргана

A B A B
A B A B

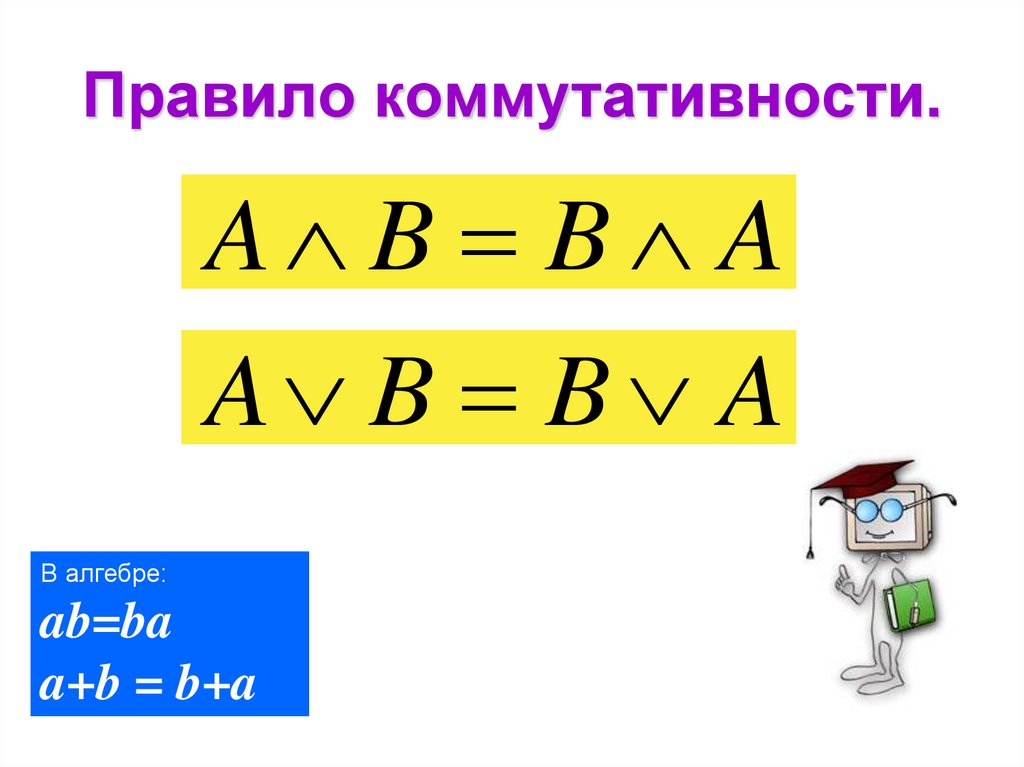
13. Правило коммутативности.

A B B A
A B B A
В алгебре:
ab=ba
a+b = b+a

14. Правило ассоциативности

A B C A B C
A B C A B C
В алгебре:
(ab)c=a(bc)
(a+b)+c =a+(b+c)

15. Правило дистрибутивности

A B C A B A C
В алгебре:
a(b+с)=ab+ac

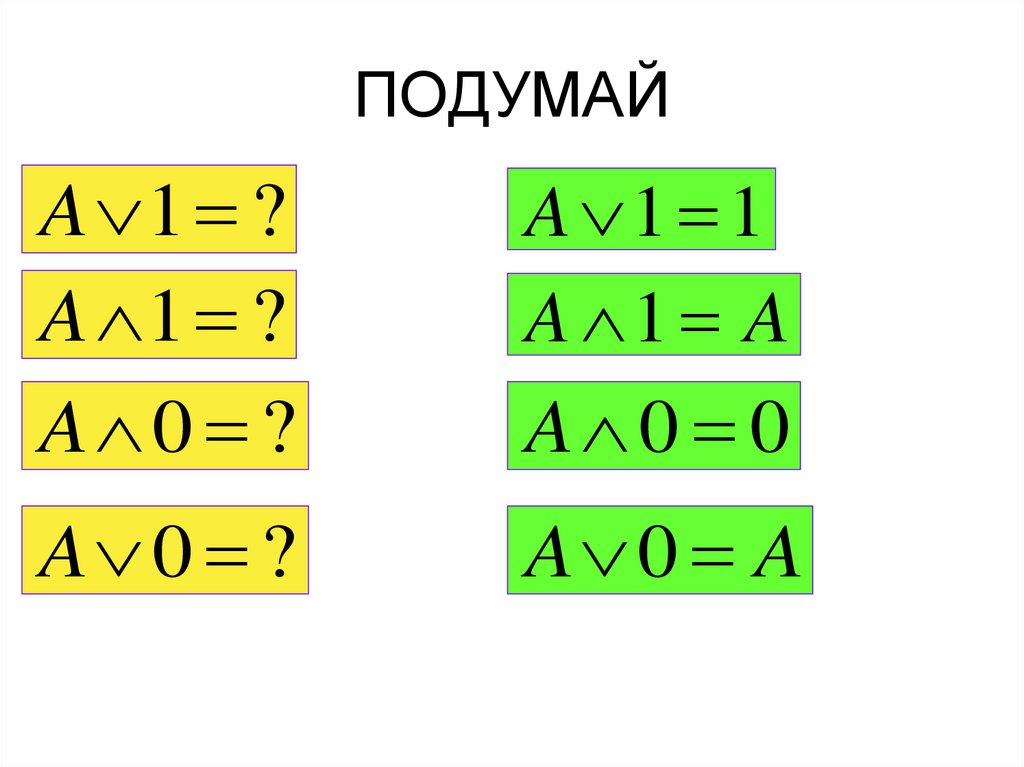
16. ПОДУМАЙ

A 1 ?
A 1 ?
A 0 ?
A 1 1
A 1 A
A 0 ?
A 0 A
A 0 0

17.

РЕШИМ ЗАДАЧИ
Упростить
логическое
выражение
A B A B
(А &. В) v (A & ¬В)
A B A B
=А
Попробуйте привлечь на
помощь алгебру.
A B C A B A B

18.

РЕШИМ ЗАДАЧИ
Упростить
логическое
выражение:
x y x y
=0
Попробуйте привлечь на
помощь алгебру.
A B A B
A B A B
A B C A B A B

19.

РЕШИМ ЗАДАЧИ
Упростить
логическое
выражение:
A B A B
x&y x y x
=1
Попробуйте привлечь на
помощь алгебру.
A B A B
A B C A B A B

20.

РЕШИМ ЗАДАЧИ
Упростить
логическое
выражение:
A B A B
x y & x y & x y
=
Попробуйте привлечь на
помощь алгебру.
y&x
A B A B
A B C A B A B

21.

РЕШИМ ЗАДАЧИ
Упростить
логическое
выражение:
A B A B
x y x y z x z
= x y y z
Попробуйте привлечь на
помощь алгебру.
A B A B
A B C A B A B
Подсказка: последнее слагаемое
домножить на единицу, т.е. на (у+у)

22.

РЕШИМ ЗАДАЧИ
Упростить
логическое
выражение:
A B A B
x& y z
A B A B
x y &z
Попробуйте привлечь на
помощь алгебру.
A B C A B A B

23.

РЕШИМ ЗАДАЧИ
Упростить
логическое
выражение:
A B A B
x y x y z x z p
x ( y p)
Попробуйте привлечь на
помощь алгебру.
A B A B
A B C A B A B

24. Домашнее задание

1. Докажите справедливость законов
Моргана, используя таблицы истинности.
2. Упростите логические выражения с
учетом правильной последовательности
выполнения логических операций:
(A v ¬A) & B
• A & (A v B) & (C v ¬B)
• A & ¬B v B & C v ¬A & ¬B
• A v ¬A & B