Похожие презентации:
Средняя линия треугольника
1.
Средняя линиятреугольника
Волкова О.А.
2.
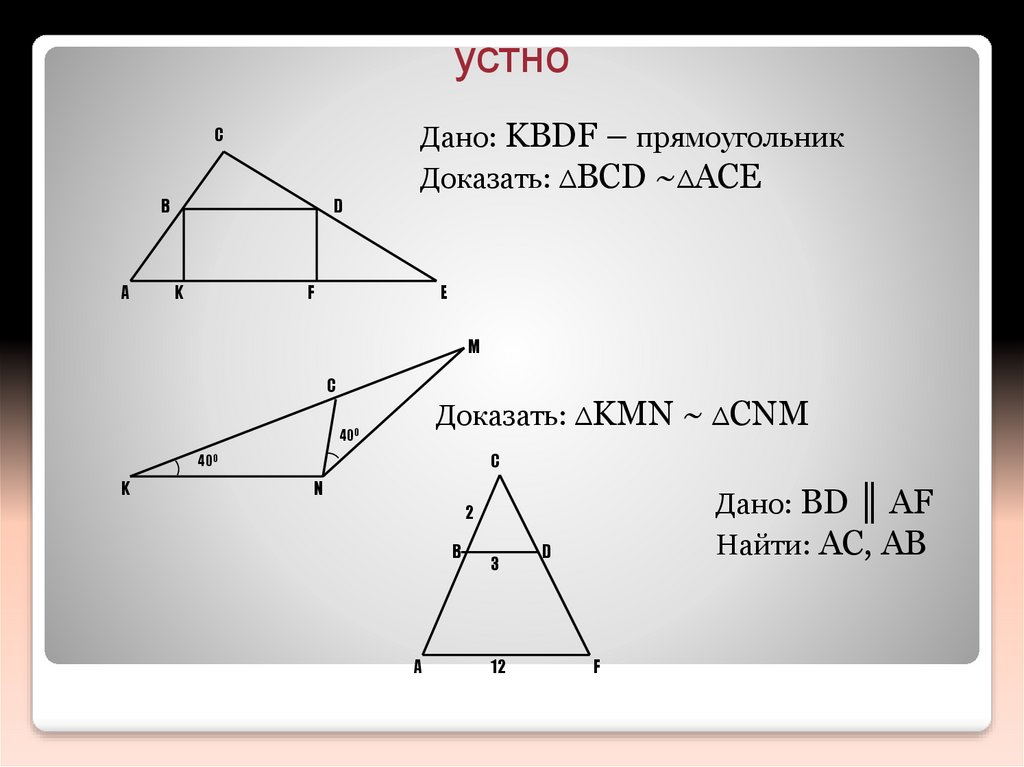
устноДано: KBDF – прямоугольник
Доказать: ∆BCD ~∆ACE
C
B
A
D
K
F
E
M
C
Доказать: ∆KMN ~ ∆CNM
400
C
400
K
N
Дано: BD ║ AF
Найти: AC, AB
2
B
A
3
12
D
F
3.
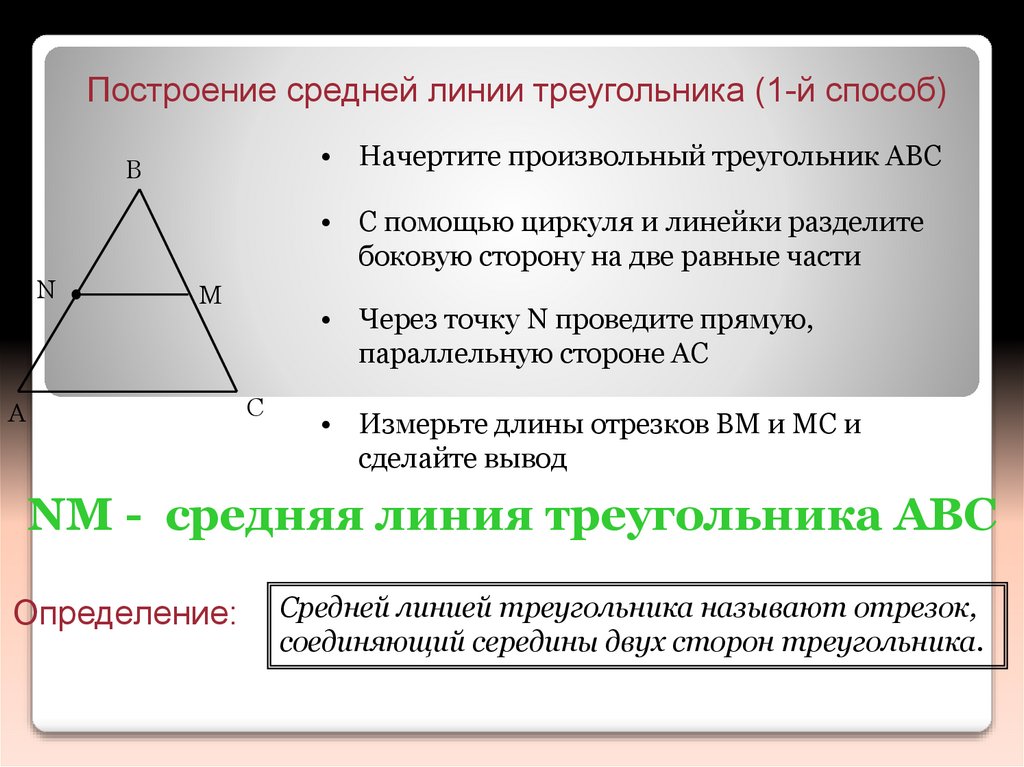
Построение средней линии треугольника (1-й способ)• Начертите произвольный треугольник ABC
B
• С помощью циркуля и линейки разделите
боковую сторону на две равные части
N
M
• Через точку N проведите прямую,
параллельную стороне AC
C
A
• Измерьте длины отрезков BM и MC и
сделайте вывод
NM - средняя линия треугольника ABC
Определение:
Средней линией треугольника называют отрезок,
соединяющий середины двух сторон треугольника.
4.
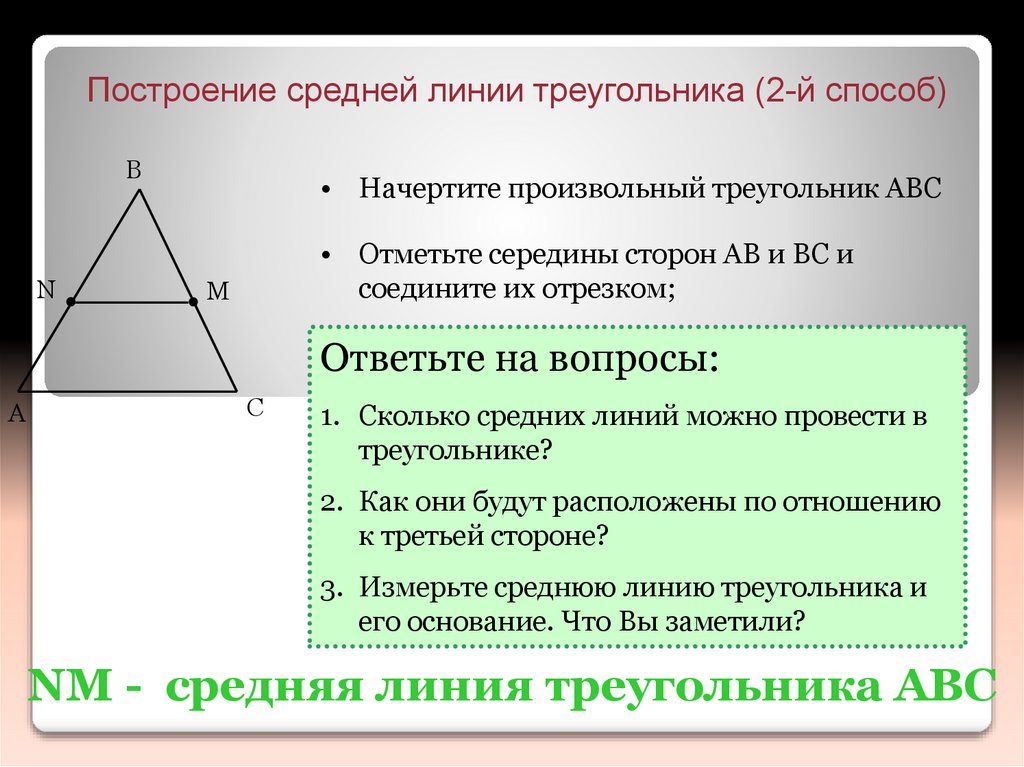
Построение средней линии треугольника (2-й способ)B
N
• Начертите произвольный треугольник ABC
• Отметьте середины сторон AB и BC и
соедините их отрезком;
M
Ответьте на вопросы:
A
C
1. Сколько средних линий можно провести в
треугольнике?
2. Как они будут расположены по отношению
к третьей стороне?
3. Измерьте среднюю линию треугольника и
его основание. Что Вы заметили?
NM - средняя линия треугольника ABC
5.
Средняя линия треугольника параллельна одной изего сторон и равна половине этой стороны.
Теорема:
B
1
N
Дано:
M
2
∆ABC, M Є BC, N Є AB.
NM-средняя линия.
Доказать: NM ║ AC, NM = ½ AC
Доказательство:
C
A
1. ∆BNM ~ ∆ABC по 2 п.п.т.(LB–общий, BM:BC = BN:BA = ½),
значит L1 = L2 и NM:AC = ½;
Т.е. NM=1/2AC
2. Т.к. L1 = L2 (из подобия треугольников) , а они
соответственные при прямых NM и AC и секущей АВ, то
NM ║ AC.
6.
BB
2
3
N
L
2
A
3
3
M
3
C
A
C
B
4
32°
2
K
G
F
3
2
C
32 °
A
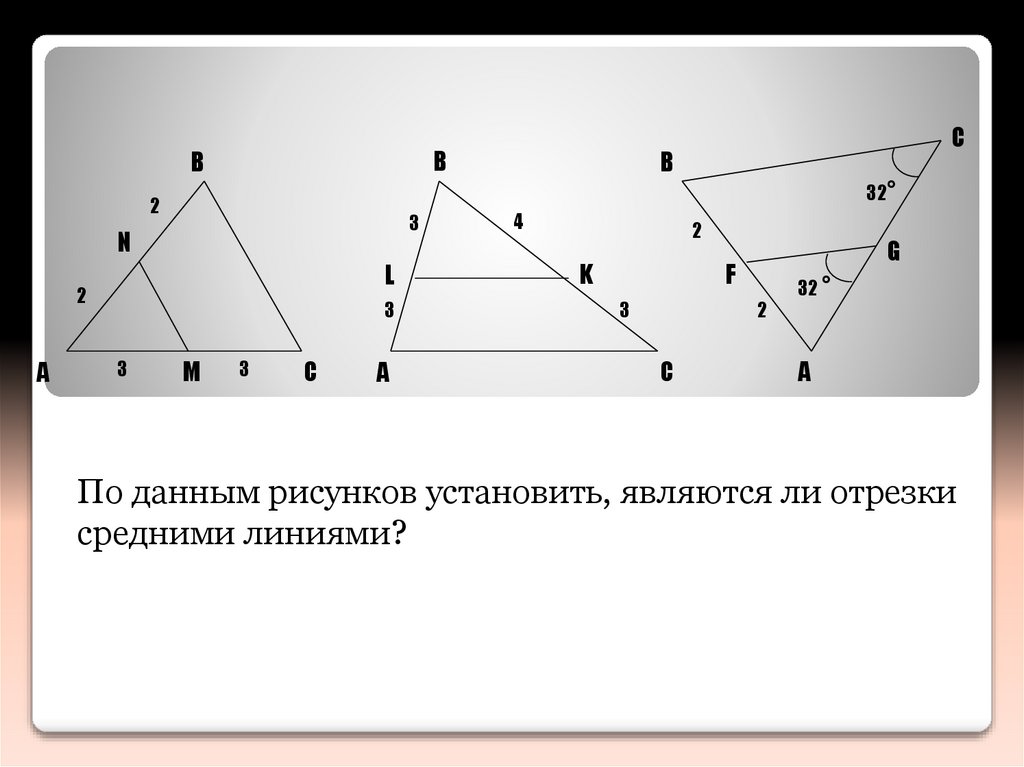
По данным рисунков установить, являются ли отрезки
средними линиями?


 Математика
Математика








