Похожие презентации:
Средняя линия треугольника
1.
Применение подобияСРЕДНЯЯ ЛИНИЯ
ТРЕУГОЛЬНИКА
к доказательству теорем
Методическая разработка урока учителя математики
МАОУ СОШ №3 г. Курганинска Краснодарского края
Коротковой Аси Эдиковны
8 класс
Л.С. Атанасян
геометрия 7-9
2.
Учиться можно тольковесело…
Чтобы переваривать
знания, надо поглощать
их с аппетитом.
Анатоль Франс
1844 - 1924
3.
Тема:Средняя линия
треугольника
Дать определение средней линии
треугольника.
Цель урока
Доказать теорему о средней линии
треугольника.
Доказать теорему о пересечении
медиан треугольника.
4. Первый признак подобия треугольников
Если два угла одноготреугольника равны
двум углам другого
треугольника, то
такие треугольники
подобны.
5. Второй признак подобия треугольников
Если две стороны одноготреугольника
пропорциональны двум
сторонам другого
треугольника и углы,
заключенные между
этими сторонами, равны,
то такие треугольники
подобны.
6. Третий признак подобия треугольников
Если три стороныодного треугольника
пропорциональны
трем сторонам
другого
треугольника, то
такие треугольники
подобны.
7. Основное понятие урока
8.
Определение. Средней линией треугольника называетсяотрезок, соединяющий середины двух его сторон.
С
А
В
Сколько средних линий можно построить в треугольнике?
9.
Теорема. Средняя линия треугольника параллельна однойиз его сторон и равна половине этой стороны.
Дано:
ABC, МN – средняя линия
Доказать: МN II АС, MN = 1
2 АС
B
Доказательство:
BM
BA
М
N
BN
BC
MBN
=
1
2
ABC
по 2 признаку
MN
AC
А
=
В общий ,
=
1
1 АС
MN
=
;
2
2
C 1= 2 , значит, МN II АС.
10. Диктант. Задание №1
Вариант 1Две стороны
треугольника
соединили отрезком,
непараллельным
третьей стороне.
Является ли этот
отрезок средней
линией данного
треугольника?
Вариант 2
Точки А и В являются
серединами двух
сторон треугольника.
Как называется отрезок
АВ?
11. Диктант. Задание №2
Вариант 1Вариант 2
Найти: BD
В
Найти: КМ
K
7 см
7 см
M
A
D
12. Диктант. Задание №3
BM
A
Вариант 1
N
K
МК=3, KN=4, MN=5
Найти периметр
треугольника АВС.
C
Вариант 2
АВ=3м, ВС=5м, АС=4м.
Найти периметр
треугольника MNK.
13. Диктант. Задание №4
Вариант 1Концы отрезка АВ
лежат на сторонах
треугольника, а его
длина равна половине
третьей стороны.
Обязательно ли: АВ –
средняя линия этого
треугольника?
Вариант 2
Концы отрезка MN
лежат на сторонах
треугольника. Отрезок
MN параллелен
третьей стороне и
равен его четверти.
Обязательно ли: MN –
средняя линия этого
треугольника?
14. Диктант. Задание №5
Вариант 1Периметр треугольника
равен 5,9 см. Найти
периметр треугольника,
отсекаемого одной из его
средних линий.
Вариант 2
Периметр треугольника
равен 7,3 см. Найти
периметр треугольника,
отсекаемого одной из его
средних линий.
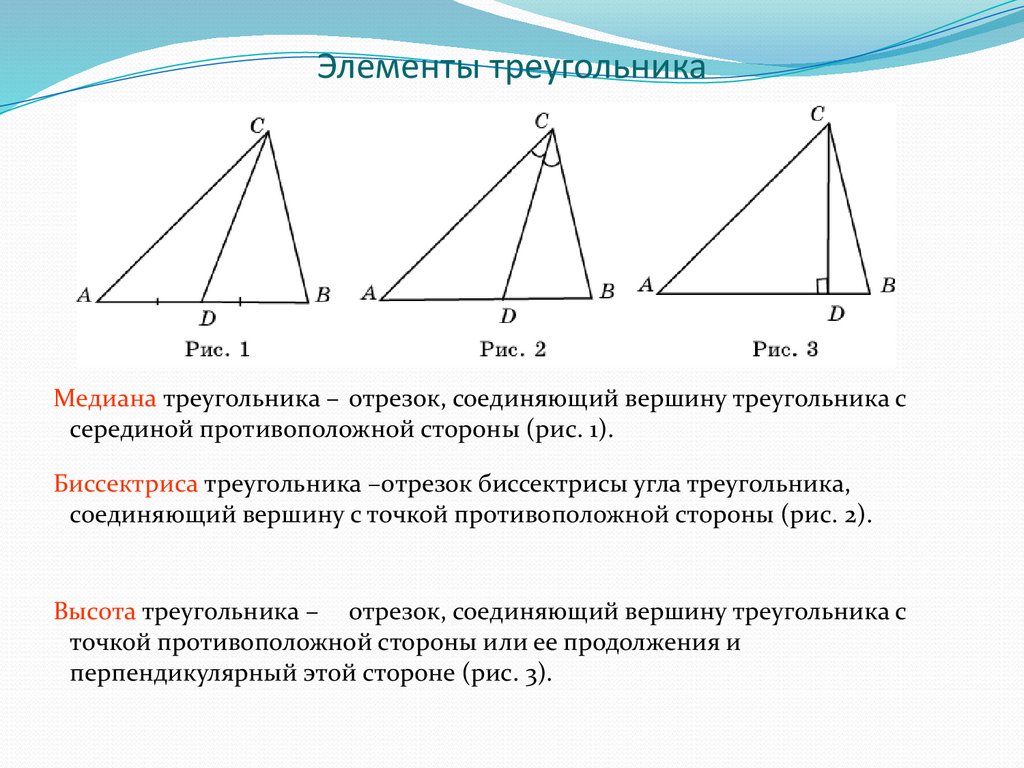
15. Элементы треугольника
Медиана треугольника – отрезок, соединяющий вершину треугольника ссерединой противоположной стороны (рис. 1).
Биссектриса треугольника –отрезок биссектрисы угла треугольника,
соединяющий вершину с точкой противоположной стороны (рис. 2).
Высота треугольника – отрезок, соединяющий вершину треугольника с
точкой противоположной стороны или ее продолжения и
перпендикулярный этой стороне (рис. 3).
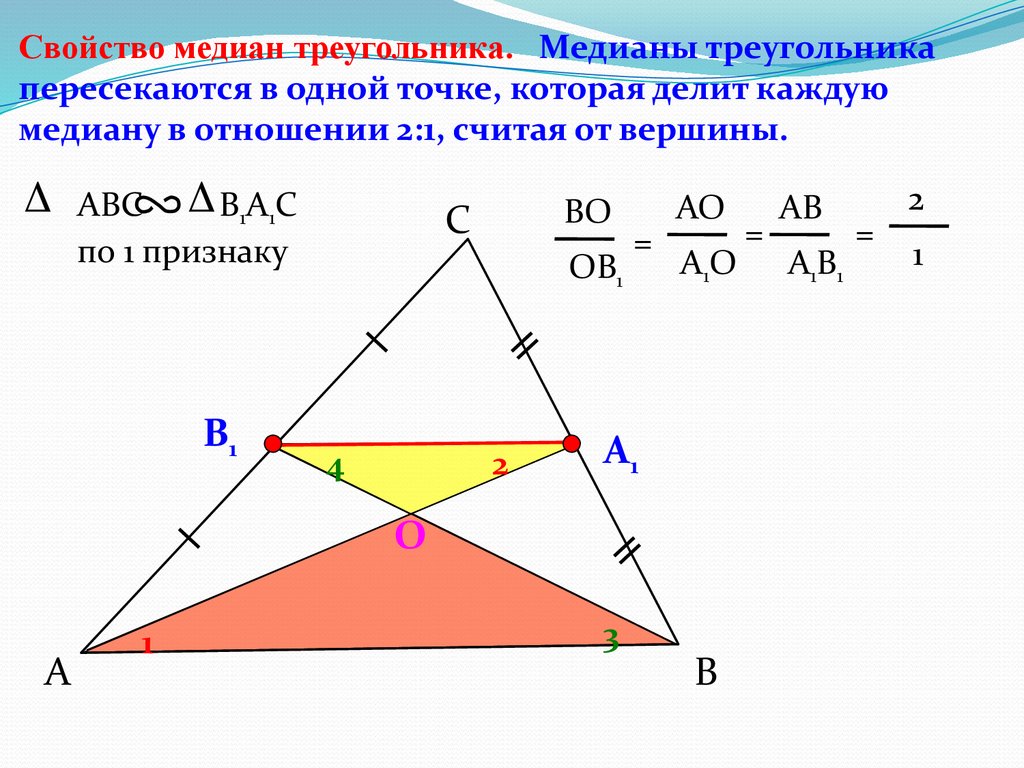
16.
Свойство медиан треугольника. Медианы треугольникапересекаются в одной точке, которая делит каждую
медиану в отношении 2:1, считая от вершины.
AВС В1А1С
по 1 признаку
В1
ВО
С
ОВ1
4
2
=
АО
А1 О
А1
О
А
1
3
В
=
АВ
А1В1
=
2
1
17.
Равновеликие треугольникиа||b
C
h
D
F
h
а
h
b
A
B
У Δ АСВ, Δ АDB, Δ AFB основание АВ, а высоты,
проведенные к АВ равны (как расстояния между
параллельными прямыми).
Значит SABC=SABD=SABF
18.
Следствие 1Медиана треугольника делит его на два
равновеликих треугольника.
В
S ABM S MBC
А
М
С
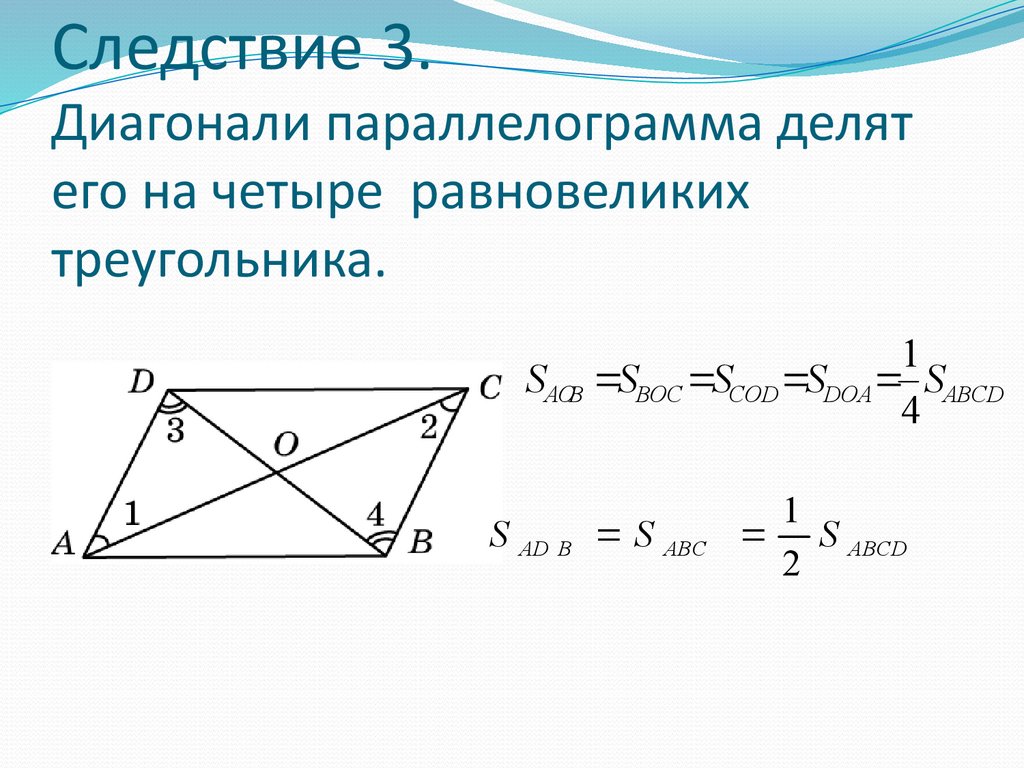
19. Следствие 3. Диагонали параллелограмма делят его на четыре равновеликих треугольника.
1SAOВ SBOC SCOD SDOA SABCD
4
S AD В S ABC
1
S ABCD
2
20. Следствие 3.
Медианы треугольника делят его на шестьравновеликих треугольников.
S AOC1 S BOC1 S BOA1 S COA1 S COB1 S AOB1
1
S ABC
6
В
С1
А
О
В1
А1
С
21. Следствие 3.
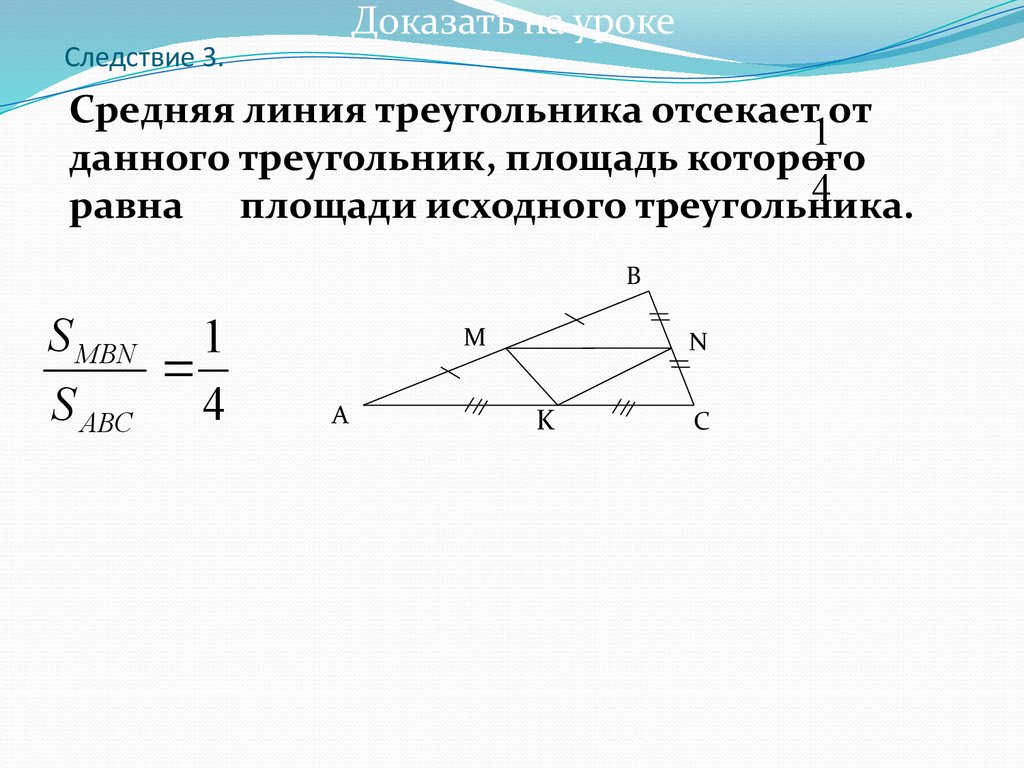
Доказать на урокеСледствие 3.
Средняя линия треугольника отсекает от
1
данного треугольник, площадь которого
4
равна площади исходного треугольника.
B
S MBN 1
S ABC 4
M
A
N
K
C
22.
ЗадачаМедианы ВК и ЕМ треугольника ВСЕ пересекаются в
точке О. Найти SMOK:SCMK.
Е
К
О
В
М
С
Решение. Обозначим SАВС = 1. SМЕС =
½. В треугольнике СМЕ МК –
медиана => SСМК = SМКЕ =
½ SМЕС = ¼.
В треугольнике МКЕ (по свойству
точки пересечения медиан) ЕО:ОМ
= 2:1 =>SЕКО : SМОК = 2:1, т.е. SМОК = ⅓
SМКЕ = ⅓·¼ = 1/12.
SMOK:SCMK = (1/12) : (1/4) = 1:3.
23. Решите задачу устно по готовому чертежу.
ВАА1, ВВ1, СС1 –
медианы треугольника.
Доказать:
А1
С
1
А
S AOC1 = S BOC1
S AOB= 2 S A1OB
S AOC1 = 1/6 S АВС
О
В
1
С
24.
Итог урокаОтрезок, соединяющий середины двух сторон треугольника,
называется средней линией треугольника.
Средняя линия треугольника параллельна одной из его сторон и
равна половине этой стороны.
Медианы треугольника пересекаются в одной точке, которая делит
каждую медиану в отношении 2 : 1, считая от вершины.
Средняя линия треугольника отсекает от данного треугольник,
площадь которого равна ¼ площади исходного.
Три средние линии треугольника разбивают его на 4 равоновеликих
треугольника, площадь каждого из них равна ¼ площади исходного.
25. Домашнее задание
П. 62, вопросы 8, 9(стр. 160)
Задачи № 616, 571.
Спасибо за урок!





















 Математика
Математика








