Задачи на смеси. Алгебра. 8 класс

1.

Тема урока: «Задачи на смеси
Алгебра 8 класс.
и сплавы».
Подготовила: учитель высшей
категории МАОУ «Гимназия №33»
г.Улан-Удэ Р.Бурятия Кузнецова В.А

2.

Цель урока: научиться решать задачи на смеси сплавы.
• Формируемые результаты:
• Предметные: формировать умение решать текстовые задачи с
помощью уравнений и систем уравнений.
• Личностные: формировать интерес к изучению темы и желание
применять приобретенные знания и умения, развивать
логическое мышление.
• Метапредметные: формировать умение использовать
приобретенные знания в практической деятельности, развивать
рефлексивное мышление.

3.

Процент-сотая часть числа
• 1%=0,01
• 10%=0,1
• Нахождение а% от числа b
• Найти 3% от 400, 3%=0,03,
400*0,03=12
• Нахождение числа m, если b это а%.
• 18 это 6% от числа m. Ставим пропорцию: 18 - 6%
Х -100%, х=(18*100):6=300
• Нахождение концентрации раствора.
• Весь раствор а, вещества в нем b, концентрация равна: b/а*100%

4.

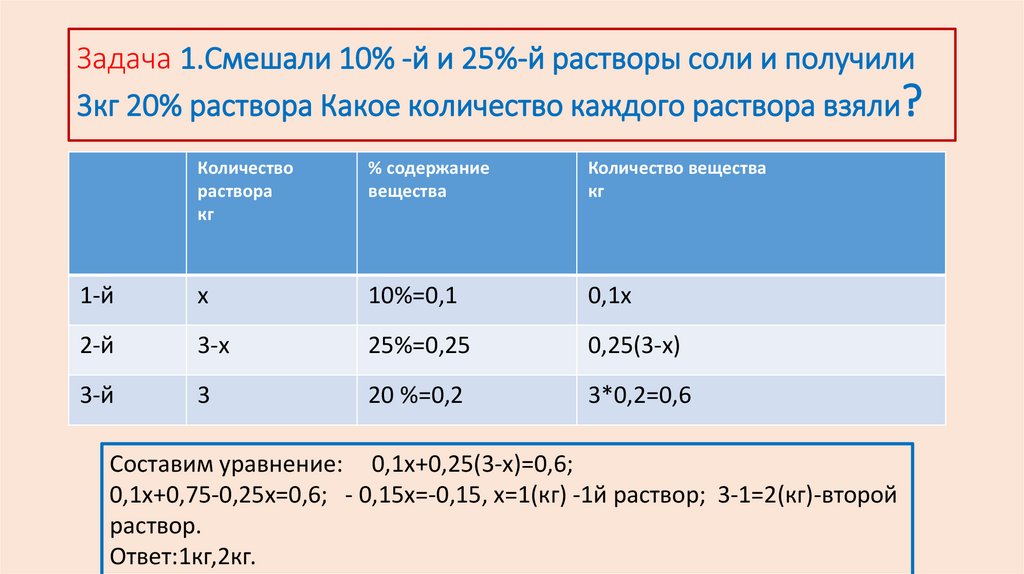
Задача 1.Смешали 10% -й и 25%-й растворы соли и получили
3кг 20% раствора Какое количество каждого раствора взяли?
Количество
раствора
кг
% содержание
вещества
Количество вещества
кг
1-й
х
10%=0,1
0,1х
2-й
3-х
25%=0,25
0,25(3-х)
3-й
3
20 %=0,2
3*0,2=0,6
Составим уравнение: 0,1х+0,25(3-х)=0,6;
0,1х+0,75-0,25х=0,6; - 0,15х=-0,15, х=1(кг) -1й раствор; 3-1=2(кг)-второй
раствор.
Ответ:1кг,2кг.

5.

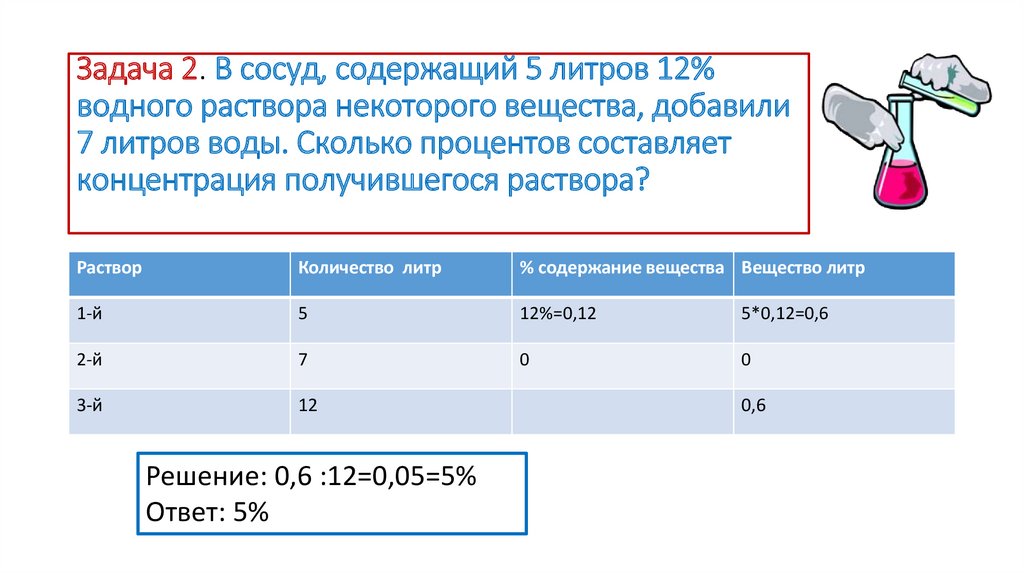
Задача 2. В сосуд, содержащий 5 литров 12%
водного раствора некоторого вещества, добавили
7 литров воды. Сколько процентов составляет
концентрация получившегося раствора?
Раствор
Количество литр
% содержание вещества Вещество литр
1-й
5
12%=0,12
5*0,12=0,6
2-й
7
0
0
3-й
12
Решение: 0,6 :12=0,05=5%
Ответ: 5%
0,6

6.

Задача 3.Смешали 4 литра 15% водного раствора
некоторого вещества с 6 литрами 25% водного
раствора этого же вещества. Сколько процентов
составляет концентрация получившегося раствора?
Раство Количество
%-е
Вещество литров
р
литров
содержание
вещества
1-й
4
15%=0,15
4*0,15=0,6
2-й
6
25%=0,25
3-й
4+6=10
6*0,25=1,5
0,6+1,5=2,1
2,1
=0,21=21%.
10
Решение:
Ответ: 21%

7.

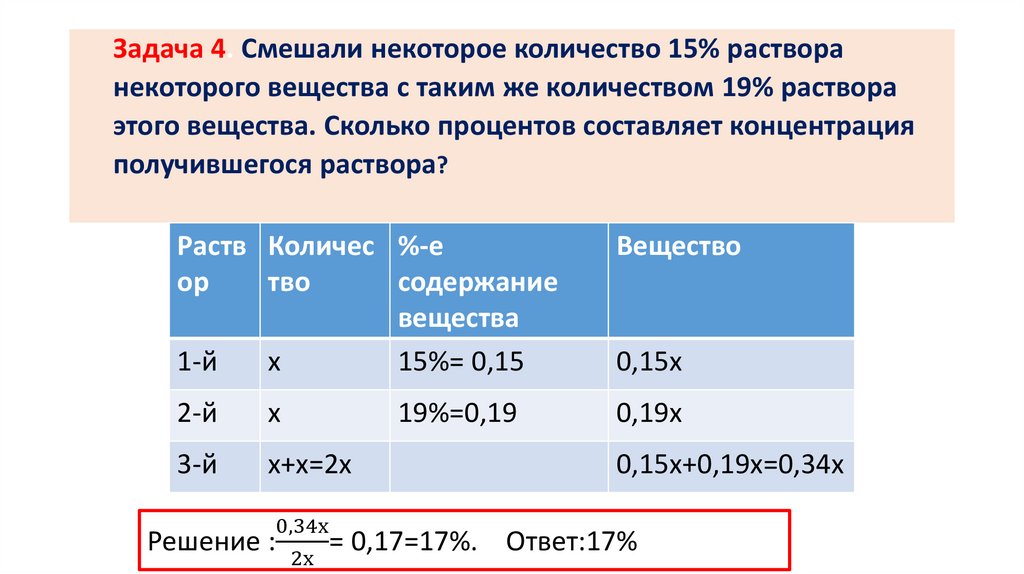
Задача 4. Смешали некоторое количество 15% раствора
некоторого вещества с таким же количеством 19% раствора
этого вещества. Сколько процентов составляет концентрация
получившегося раствора?
Раств Количес %-е
ор
тво
содержание
вещества
1-й
х
15%= 0,15
Вещество
2-й
х
0,19х
3-й
х+х=2х
Решение
0,34х
:
=
2х
19%=0,19
0,15х
0,15х+0,19х=0,34х
0,17=17%. Ответ:17%

8.

Задача 5. Первый сплав содержит 10%
меди, второй — 40% меди. Масса второго
сплава больше массы первого на 3 кг. Из
этих двух сплавов получили третий сплав,
содержащий 30% меди. Найдите массу
третьего сплава. Ответ дайте в
килограммах.

9.

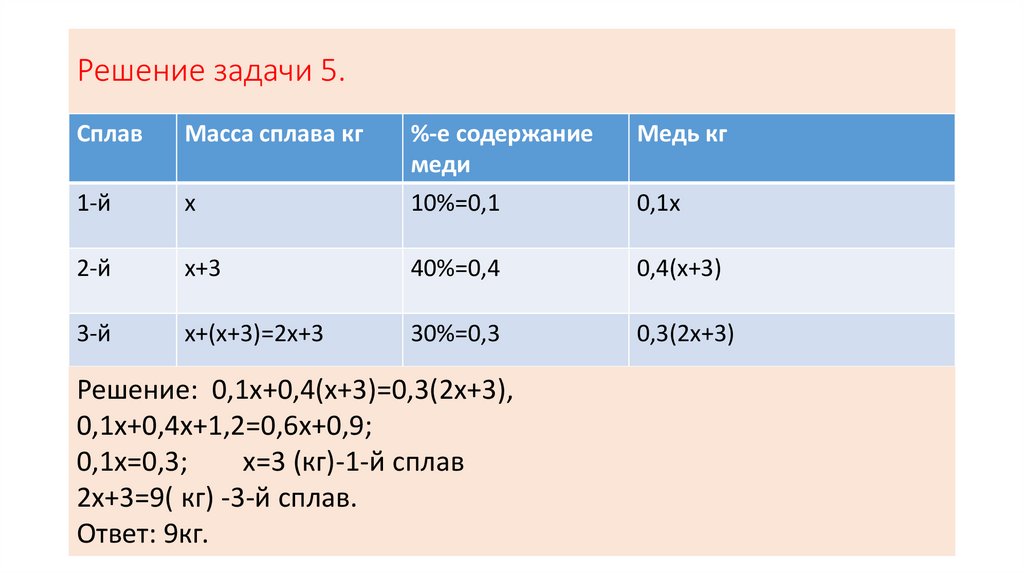
Решение задачи 5.
Сплав
Масса сплава кг
Медь кг
х
%-е содержание
меди
10%=0,1
1-й
2-й
х+3
40%=0,4
0,4(х+3)
3-й
х+(х+3)=2х+3
30%=0,3
0,3(2х+3)
Решение: 0,1х+0,4(х+3)=0,3(2х+3),
0,1х+0,4х+1,2=0,6х+0,9;
0,1х=0,3;
х=3 (кг)-1-й сплав
2х+3=9( кг) -3-й сплав.
Ответ: 9кг.
0,1х

10.

Задача
6.Смешав
30% и 60% растворы кислоты
Задача
6
и добавив 10 кг чистой воды, получили 36%
Смешав
30%
и
60%
растворы
кислоты
и
раствор кислоты. Если бы вместо 10 кг воды
добавив
10
кг
чистой
воды,
получили
36%
добавили 10 кг 50% раствора той же кислоты,
раствор
кислоты.
бы кислоты.
вместо 10
кг
то получили
бы 41%Если
раствор
Сколько
воды
добавили
кг 50%использовали
раствора тойдля
же
килограммов
30%10
раствора
кислоты,
получили бы 41% раствор
получениято
смеси?
кислоты. Сколько килограммов 30%
раствора использовали для получения
смеси?

11.

Решение задачи 6.
Раствор
Масса раствора кг
% -е содержание
Вещество(кислота) кг
1-й
х
30%=0.3
0,3х
2-й
у
60%=0,6
0,6у
3-й (вода)
10
0
0
Полученный
А
х+у+10
36%=0,36
0,36(х+у+10)
3-й
10
50%=0,5
5
Полученный
Б
х+у+10
41%=0,41
0,41(х+у+10)
0,3х + 0,6у = 0,36(х + у + 10)
ቊ
, отсюда, вычитая из второго
0,3х + 0,6у + 5 = 0,41(х + у + 10)
уравнения 1-е и преобразуя результат, имеем: х+у=90, х=90-у. Подставим в 1-е
уравнение х=90-у, решим: у=30кг,значит х=60кг.
Ответ: 60кг 30% раствора взяли.

12.

Решите самостоятельно старинные задачи.(Из «Арифметика»
А.П.Кисилева)
• Задача1. 30 ведер вина в 48
градусов смешано с 24
ведрами вина в 30 градусов.
Сколько градусов в смеси?
(Число градусов означает
процентное содержание
чистого спирта в вине).
• Задача 2.Смешано три сорта
муки: 15 фунтов по 8 коп,20
фунтов по 7 коп,25 фунтов по
по 4 копейки. Сколько стоит
фунт смеси?

13.

Задачи повышенного уровня для самостоятельного
решения.
• Задача 1(МИФИ).Имеется два
• Задача 2.(РЭА)Имеется два
водных раствора щелочи:
раствора кислоты в воде,
первый содержит 10% щелочи,
содержащие 40% и 60%
второй 30%.После смешивания
кислоты. Смешав эти растворы
20л первого раствора,
и добавив 5л воды, получили
некоторого количества 2-го
20%-й раствор. Если бы вместо
раствора и 10л воды получили
воды добавили 5л 80%
раствор, в котором воды
раствора, то получился бы
оказалось в 2,5 раза больше,
70%-й раствор. Сколько литров
чем щелочи. Сколько л второго
60% раствора кислоты было
раствора было взято?
первоначально?