Похожие презентации:
Комплексные числа. Числовые множества
1.
Преподаватель математикиОГАПОУ «Белгородский
техникум промышленности
и сферы услуг»
Веревкина А.А.
2.
Решите уравнениеx 1
2
3.
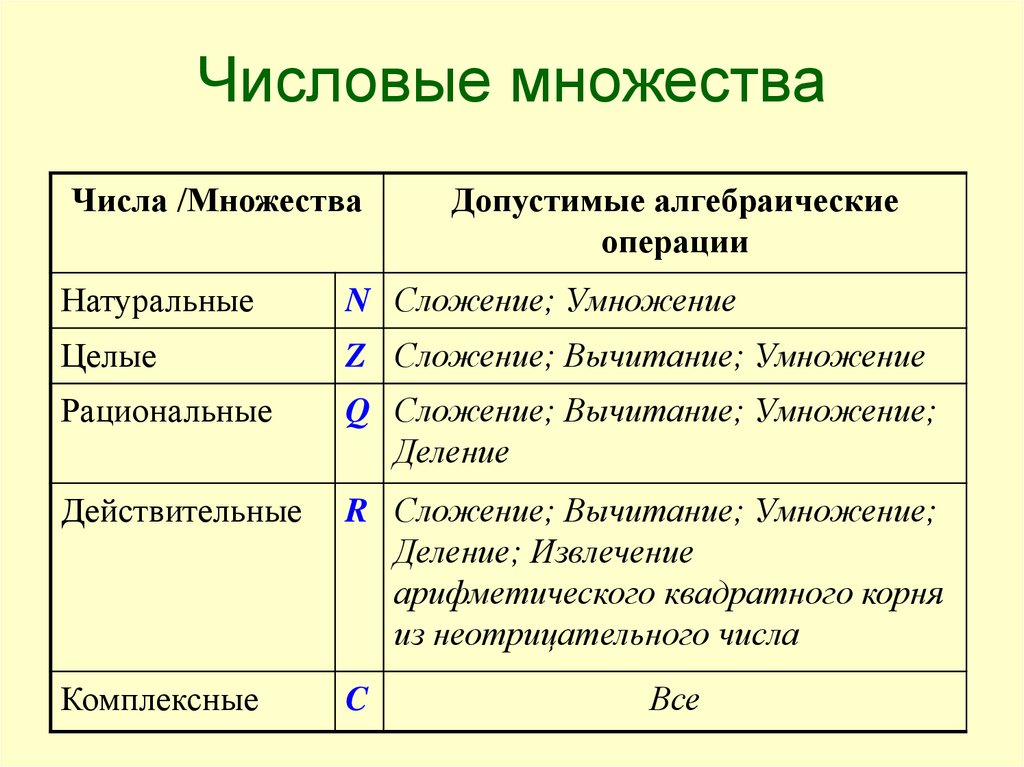
Числовые множестваЧисла /Множества
Допустимые алгебраические
операции
Натуральные
N Сложение; Умножение
Целые
Z Сложение; Вычитание; Умножение
Рациональные
Q Сложение; Вычитание; Умножение;
Деление
Действительные
R Сложение; Вычитание; Умножение;
Деление; Извлечение
арифметического квадратного корня
из неотрицательного числа
Комплексные
C
Все
4.
Множество СМножество комплексных чисел содержит
все действительные числа.
Операции
сложения,
вычитания,
умножения и деления комплексных чисел
удовлетворяют
обычным
законам
арифметических действий (сочетательному,
переместительному, распределительному).
Существует квадратный корень из -1, т.е.
существует комплексное число, квадрат
которого равен -1.
5.
Мнимая единицаi
i 1
2
- i; 2i; - 0,3i - чисто мнимые числа
6.
Степени мнимой единицыПо определению первой степенью числа i является
само число i, а второй степенью является число -1:
i1 = i; i2 = -1;
i3 = -i; i4 = 1
При любом натуральном n
i4n = 1;
i4n +2 = - 1;
i4n+1 = i;
i4n+3 = - i.
7.
Арифметические операциис мнимыми числами
ai bi a b i; ai bi a b i;
ai bi abi ab 1 ab
a bi ab i;
2
a и b — действительные числа.
3i 12i 3 12 i 15i
3i 12i 3 12 i i 36 i 2 36
i 1
i i
7
2 3
3
i i
8.
Комплексные числаКомплексным числом называют сумму
действительного числа и чисто мнимого числа.
z a bi C a R, b R,
i мнимая единица.
a Re z , b Im z
Два комплексных числа называют равными,
если равны их действительные части и равны
их мнимые части:
a bi c di a c, b d .
9.
Арифметические операциинад комплексными числами
(а + bi) + (c + di) = (а + с) + (b + d)i
(а + bi) - (c + di) = (а - с) + (b - d)i
(а + bi)·(с + di) = (ac - bd) + (ad + bc)i
a bi (a bi)(c di) ac bd bc ad
2
2 2
2 i
c di (c di)(c di) c d
c d
10.
Арифметические действия3 4i 5 7i 2 3i;
3 4i 5 7i 3 5 4 7 3 7 4 5 i 13 41i;
5 7i 5 7i 3 4i 43 i
43 1
i;
3 4i 3 4i
3 4i
25
25 25
4
2
2
2
2
1 i 1 i 1 i 1 2i 1 2i 4
11.
Сопряженные комплексные числаЕсли у комплексного числа сохранить действительную
часть и поменять знак у мнимой части, то получится
комплексное число, сопряженное данному.
Если данное комплексное число обозначается буквой z,
то сопряженное число обозначается z
z x yi; z x yi
Из всех комплексных чисел действительные числа
(и только они) равны своим сопряженным числам.
Числа a + bi и a - bi называются
сопряженными комплексными числами.
12.
Свойство сопряженныхкомплексных чисел
Сумма и произведение двух сопряженных чисел
есть число действительное.
z z (a bi ) ( a bi ) 2a
z z (a bi )( a bi ) a (bi ) a b
2
2
2
2
13.
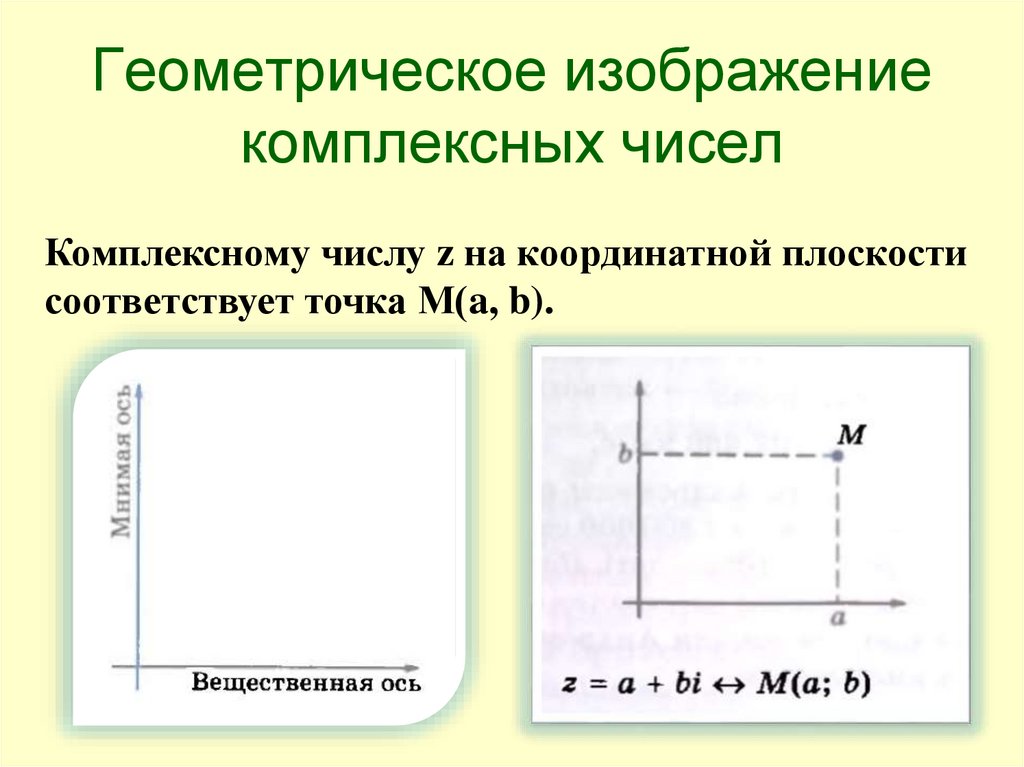
Геометрическое изображениекомплексных чисел
Комплексному числу z на координатной плоскости
соответствует точка М(a, b).
14.
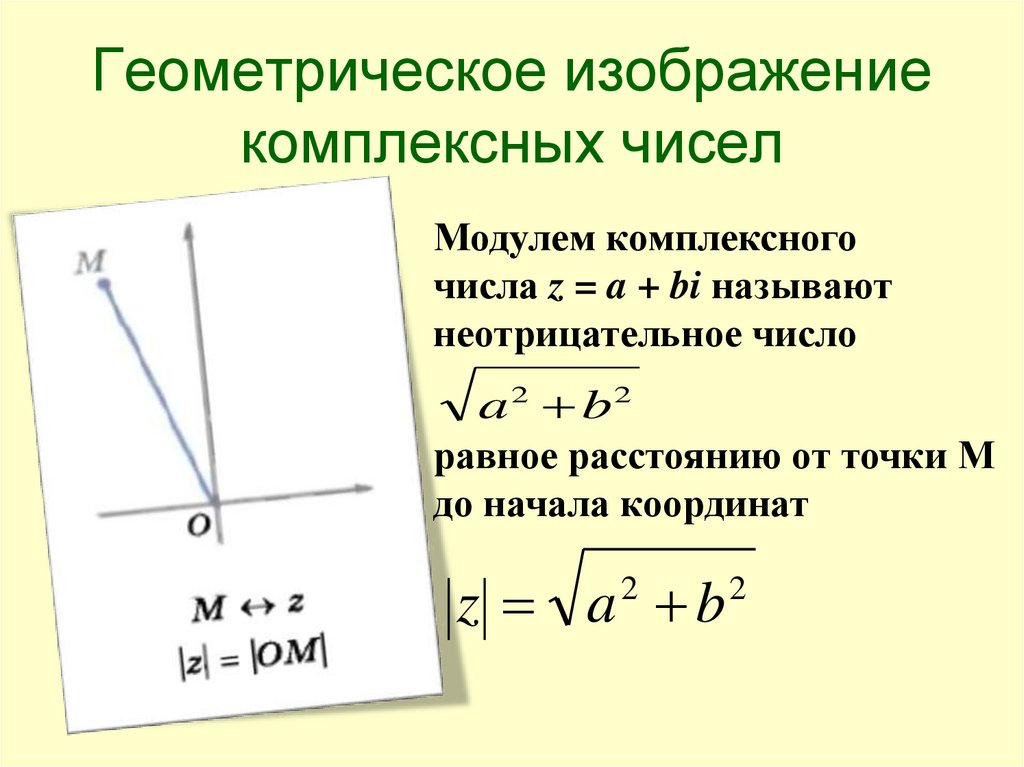
Геометрическое изображениекомплексных чисел
Модулем комплексного
числа z = a + bi называют
неотрицательное число
a 2 b2
равное расстоянию от точки М
до начала координат
z a b
2
2
15.
Геометрическое изображениекомплексных чисел
16.
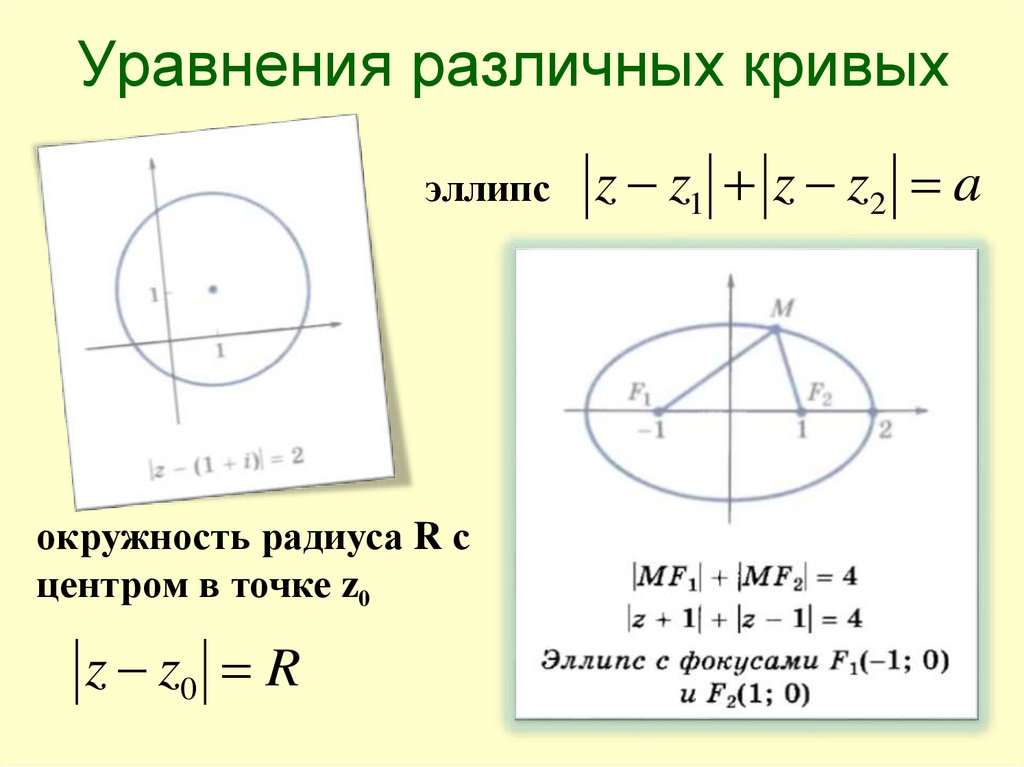
Уравнения различных кривыхэллипс
окружность радиуса R с
центром в точке z0
z z0 R
z z1 z z2 a
17.
Верны ли следующиевысказывания?
- 5 комплексное число;
- число а такое, что а2 = - 4 является действительным;
- число а такое, что а4 = 1 является действительным;
- многочлен х2+4 можно разложить на линейные
множители с комплексными коэффициентами;
- точки плоскости, удовлетворяющие условию z 1 2
лежат на окружности радиуса 1;
- если комплексное число равно сопряженному, то оно
является действительным;
- если z z , то действительная часть числа z равна
нулю
18.
Заданиядля самостоятельной работы
19.
Подведем итогиУзнали:
алгебраическую, геометрическую формы
комплексного числа.
Научились:
производить над комплексными числами операции
сложения, умножения, вычитания, деления;
переводить комплексные числа из алгебраической
формы в геометрическую;
в простейших случаях находить комплексные корни
уравнений с действительными коэффициентами.
20.
Выберите смайлик, которыйсоответствует Вашему
настроению в конце урока.
Спасибо за урок!
21.
Использованные ресурсы• Математика: учебник для учреждений нач. и
сред. проф. образования / М.И. Башмаков. М.: Издательский центр «Академия», 2012.

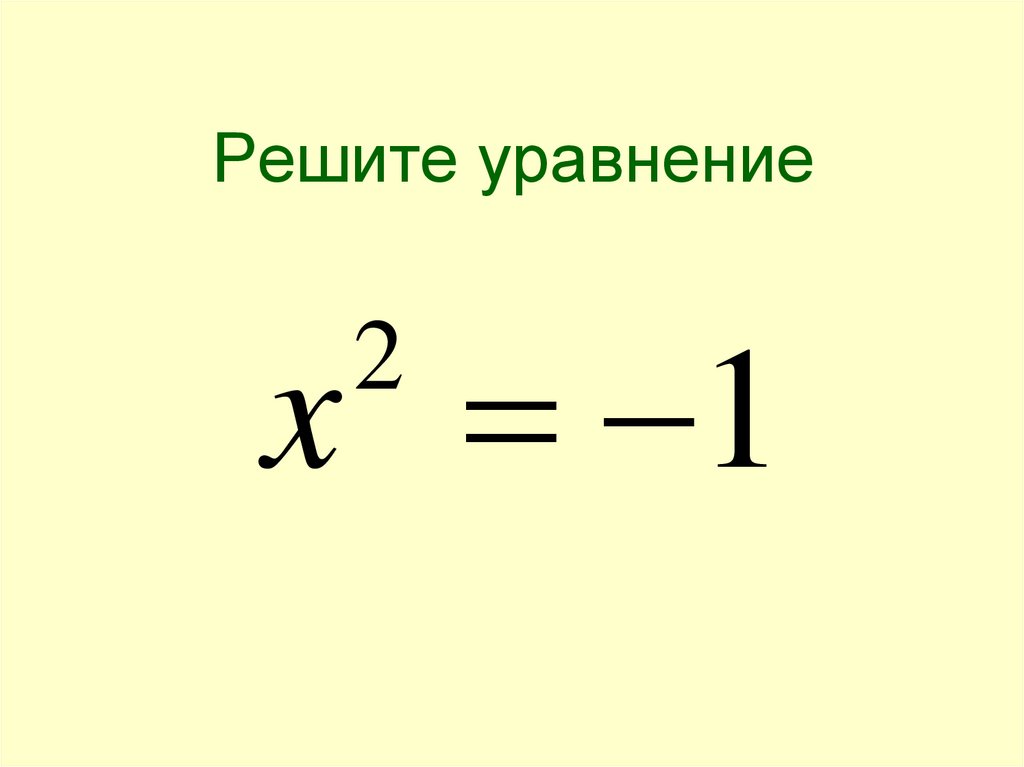















 Математика
Математика








