Похожие презентации:
Комплексные числа и действия над ними
1.
Комплексные числа идействия над ними
2.
1446,25
64
256
900
3.
МНИМАЯ ЕДИНИЦА4.
23
4
5
6
2 ; 11
ii21
i 11
;; i
i i i 1;
22
3
2
3
2
iii i ii i(i
1
)
i
(( 11))iii iii;;ii ; ( 1)i i;
233
22
44
33
2
2
3
2
4
3
2
4
3
2
ii ii ii ii ii ii (( 11)) 11;;
ii i i
i ( 1
i ) ( 1
i i i i i
i4i ii ii 11 ii i i i;; i i 1 i i;
i i 1 i i;
66
55
2
2
i5i ii ii ii ii i 66 ii 2i 5 5 i11 ;; i i i22 1;
55
44
55
44
5.
Мнимые числаi = -1, i – мнимая единица
i, 2i, -0,3i — чисто мнимые числа
Арифметические операции над чисто
мнимыми числами
3i 13i 3 13 i
16i
3i 13i 3 13 i i 39i 39
2
i i
7
i i
2 3
В общем виде правила арифметических операций с
чисто мнимыми числами таковы:
a b i;
a bi ab i;
ai bi
ai bi a b i;
ai bi abi a
2
где a и b — действительные числа.
6.
36(
1
)
36
1
i
6
36
(
1
)
36
1
6
i
36
36
(
1
)
36
1
6
i
36
36
(
1
)
36
1
6
i
36
( 1) 36 1
900
1
4
12,25
7.
Комплéксные числаЧисла вида
a + bi,
где a и b – действительные числа,
i – мнимая единица,
форма записи:
алгебраическая,
тригонометрическая
экспоненциальная (показательная)
8.
Числовая системаДопустимые
алгебраические
операции
Частично
допустимые
алгебраические
операции
Натуральные числа, N Сложение, умножение
Вычитание, деление,
извлечение корней
Целые числа, Z
Сложение, вычитание,
умножение
Деление, извлечение
корней
Рациональные числа,
Q
Сложение, вычитание,
умножение, деление
Извлечение корней из
неотрицательных чисел
Действительные
числа, R
Комплексные числа, С
Сложение, вычитание,
умножение, деление,
извлечение корней из
неотрицательных чисел
Все операции
Извлечение корней из
произвольных чисел
9.
Комплексные числаОпределение 1. Комплексным числом
называют сумму действительного числа и
чисто мнимого числа. z a bi C
a R, b R,
i мнимая единица.
a Re z , b Im z
Определение 2. Два комплексных числа
называют равными, если равны их
действительные части и равны их
мнимые части:
a bi c di a c, b d .
10.
Найти x и y из равенства:2y + 4xi = 13 – 6i;
Решение.
Используя условие равенства
комплексных чисел имеем
2y = 13, 4x = – 6, тогда
x 1,5; y 6,5.
11.
Классификация комплексных чиселКомплексные числа
a + bi
Действительные числа
b=o
Рациональные
числа
Иррациональные
числа
Мнимые числа
b≠o
Мнимые числа с
ненулевой
действительной
частью
a ≠ 0, b ≠ 0.
Чисто
мнимые
числа
a = 0, b ≠ 0.
12.
Арифметические операции надкомплексными числами
(а + bi) + (c + di) = (а + с) + (b + d)i
(а + bi) - (c + di) = (а - с) + (b - d)i
(а + bi)·(с + di) = (ac - bd) + (ad + bc)i
a bi (a bi)( c di) ac bd bc ad
2
2
i
2
2
c di (c di)( c di) c d
c d
13.
Сопряженные комплексные числаОпределение: Если у комплексного числа сохранить
действительную часть и поменять знак у мнимой части, то
получится комплексное число, сопряженное данному.
Числа a + bi и a - bi называются взаимно
сопряженными комплексными числами.
14.
z1 = 12 + 3i, z2 = 5 – 7i.Найти: а) z1 + z2; б) z1 – z2;
а) z1 + z2 =(12 + 3i) + (5 – 7i) =
=(12 + 5) + (3i – 7i) = 17 – 4i;
б) z1 – z2 =(12 + 3i) – (5 – 7i) =
=(12 – 5) + (3i + 7i) = – 7 + 10i;
15.
(2 + 3i)(5 – 7i) == (10+21) + (-14+15)i = 31+i
(5 + 3i)(5 – 3i) = 25-9i2 = 34
(2 –
2
7i)
= 4 - 28i +
2
49i
= -45-28i
16.
2 3i 2 3i 5 7i=
5 7i 5 7i 5 7i
=
11 29i
74
=
11 29
i
74 74
17.
(2 3i ) (4 i )27
4i
1 i
6 2i 1 i
4
8
i
4i =
4
i
=
1 i 1 i
2
=2
18.
Модуль комплексного числаОпределение:
Модулем комплексного числа z = a + bi
называют неотрицательное число a 2 b 2
19.
Геометрическое изображение комплексныхчисел.
Комплексному числу z на координатной плоскости соответствует
точка М(a, b).
Часто вместо точек на плоскости берут их радиусы-векторы OM
равное расстоянию от точки М до начала
координат z a 2 b 2
y
М (a, b)
b
φ
O
a
x
cos
a
и sin
b
a2 b2
a2 b2
аргумент комплексно го числа
;
20.
Тригонометрическая форма комплексного числаz r cos i sin
где φ – аргумент комплексного числа,
r=
a 2 b 2 модуль комплексного числа,
cos
a
a b
2
2
и sin
b
a b
2
2
21.
Комплексные числа идействия над ними
Практикум
№ 32.5,32.6,32.10,32.11,
32.19-32.21, 34.1, 34.2, 34.21-34.25
Контроль 15.03
Самостоятельная работа, тетради

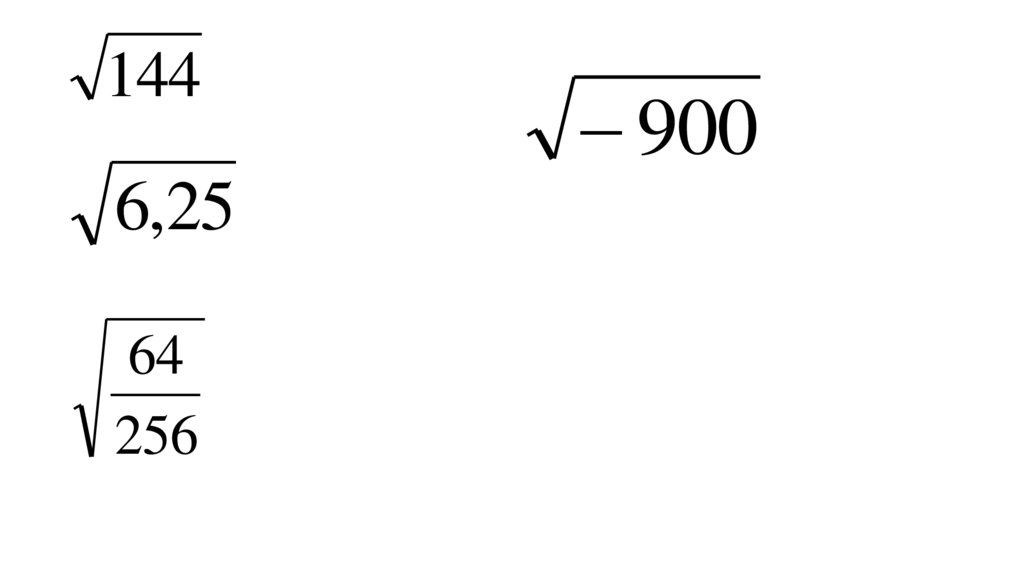

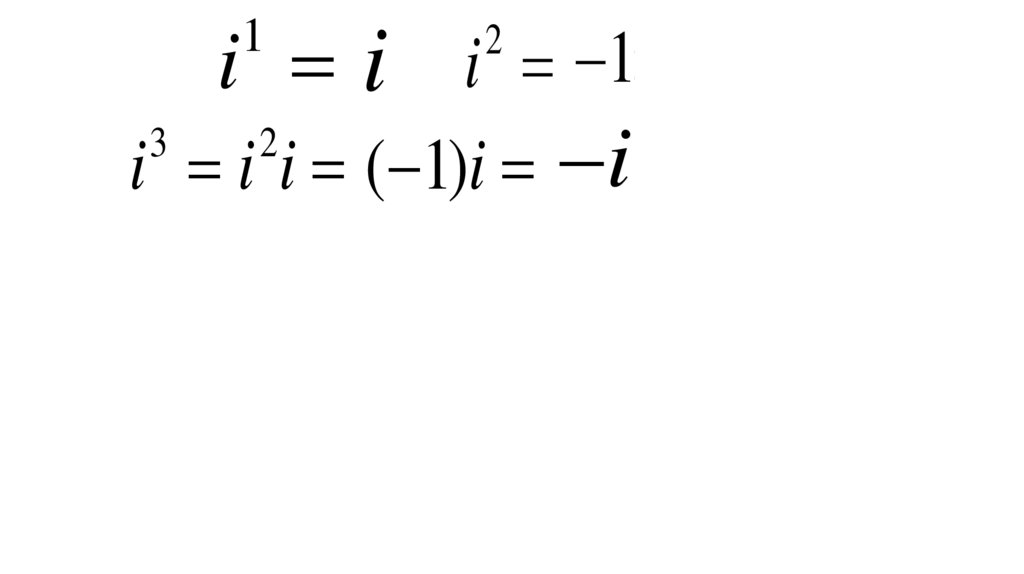









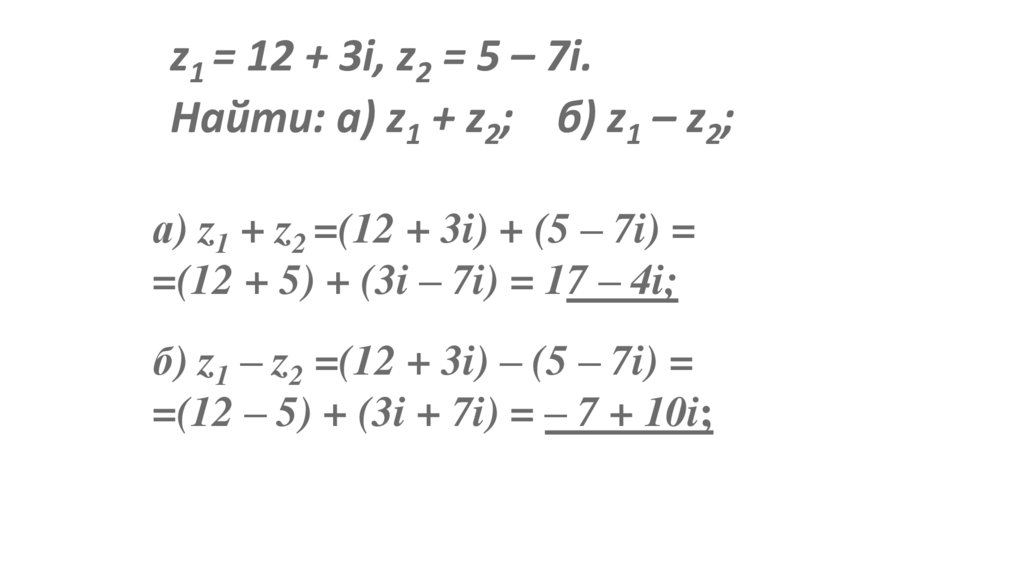

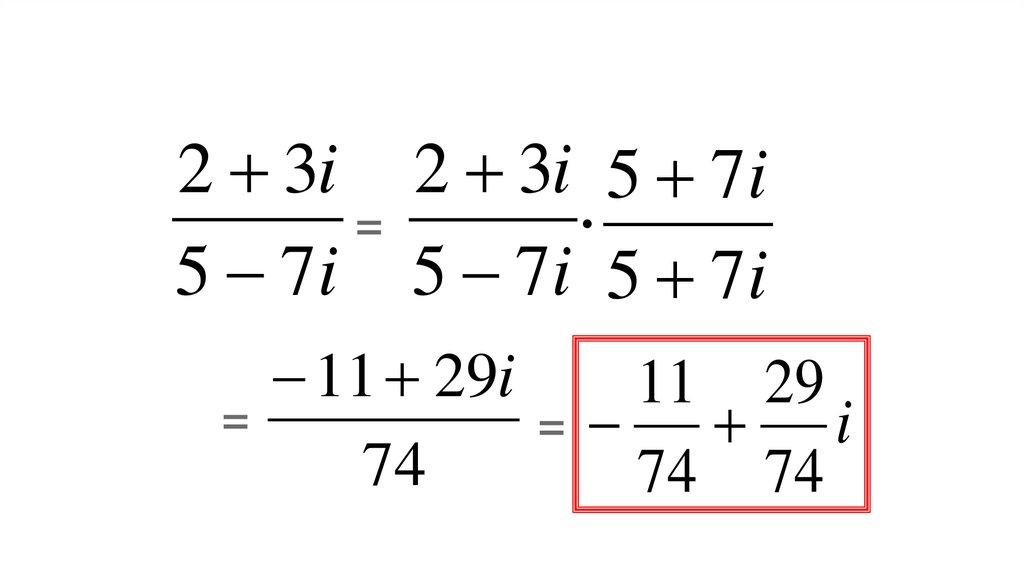





 Математика
Математика








