Функции нескольких переменных

1.

1/14
Функции нескольких переменных
Производная от функции, заданной неявно
Частные производные различных порядков
Производная по направлению
Градиент

2.

2/14
Производная от функции, заданной неявно
Теорема
Пусть непрерывная функция y от x задана неявно уравнением:
F ( x; y ) 0
где F(x;y), F’x, F’y – непрерывные функции в некоторой области D,
содержащей точку (x; y); кроме того, в этой точке F’y не равно нулю.
Тогда функция у от х имеет производную:
y
Fx
x
Fy
(1)
Найти производную неявно заданной функции e y e x xy 0
F ( x; y ) e y e x xy
По формуле (1) получаем:
y
x
Fx
Fy
Fx e x y
ex y
y
e x
Fy e y x

3.

3/14
Производная от функции, заданной неявно
Рассмотрим теперь уравнение вида:
F ( x; y ; z ) 0
(2)
Если каждой паре x, y из некоторой области соответствует одно или
несколько значений z, удовлетворяющих уравнению (2), то это
уравнение неявно определяет одну или несколько однозначных
функций z от x, y. Частные производные функции z по x, y находятся
по формулам:
z
Fx
;
x
Fz
Fy
z
y
Fz
Найти частные производные функции z по x и y
F ( x; y; z) e z x 2 y z 5
По формулам (3) получаем:
z
x
Fx
Fz
z
y
Fx 2 xy
Fy
Fz
(3)
ez x 2y z 5 0
Fy x 2
Fz e z 1

4.

4/14
Частные производные различных порядков
Пусть имеем функцию двух переменных
z f ( x; y )
Частные производные z ’x, z ’y также являются функциями двух
переменных x и y. Поэтому от них можно снова находить частные
производные.
Частных производных от ФДП четыре, так как каждую из функций z ’x,
z ’y можно дифференцировать по x и по y.
Вторые частные производные обозначаются так:
функция z сначала
2z
2z
функция
z дифференцируется
дифференцируется
по х , а потом
z
z
xy
xx
2
последовательно
два раза по x
x y
результат дифференцируется
по y.
x
2z
z yy
2
y
функция z сначала
функция z дифференцируется
2z
дифференцируется по у , а потом
z yx
последовательно
два раза по у
y x
результат дифференцируется по х.

5.

5/14
Частные производные различных порядков
Найти частные производные второго порядка
z y 2e x x 2 y 3 1
z
y 2e x x 2 y 3 1 x y 2e x 2xy 3
x
z
y 2e x x 2 y 3 1 y 2ye x 3 x 2 y 2
y
2z
2
yx x
x
22zz
2
xy y
2 2
y 22ye
e x x 66xxy
y
2 xx
yye
e 2y
2
6 xy3 2

6.

6/14
Частные производные различных порядков
Производные второго порядка можно снова дифференцировать как
по х, так и по y.
Частной производной n – ого порядка называется первая
производная от производной n -1 порядка, например:
nz
x p y n p
Для функции любого
числа
переменных частные производные
функция
z сначала
высших дифференцируется
порядков определяются
аналогично:
p раз по
х,а
потом результат дифференцируется
u
u
2 2 x y 2 Найти
ze
n - p раз2по y.
4
u
2u
2
x
x y z
x 4z e
4u
2
x y z
2
2x y 2
x 2z e
x
3u
2
x y
z 16yze 2x y
2
2x y 2
y 8yz e
2
2
2x y 2

7.

7/14
Частные производные различных порядков
Теорема
Если функция z = f(x; y) и ее частные производные f ’x ; f ’y ;f ’’xy ; f ’’yx
определены и непрерывны в точке М(x; y) и в некоторой ее
окрестности, то в этой точке:
2z
2z
x y y x
Следствие
Если частные производные
nz
;
p
n p
x y
nz
непрерывны, то
n p
p
y x
nz
nz
n p p
p
n p
x y
y x

8.

8/14
Производная по направлению
Пусть в пространстве имеется область D , в которой задана функция
трех переменных u = f(x; y; z). В этом случае говорят, что в области
D задано скалярное поле.
Возьмем в области D точку M(x; y; z).
z
M1
Δz
M
Δx
x
Таким образом,
cos ; cos ; cos
На векторе s на расстояние Δs от его
начала рассмотрим точку
Δy
0
Проведем из точки М вектор s,
направляющие косинусы которого равны:
y
M1(x+Δх; y+Δy; z+Δz)
s x 2 y 2 z 2
Будем предполагать, что функция u непрерывна и имеет
непрерывные частные производные в области D.

9.

9/14
Производная по направлению
z
M1
Δz
M
γ
β
Δxα Δy
y
0
x
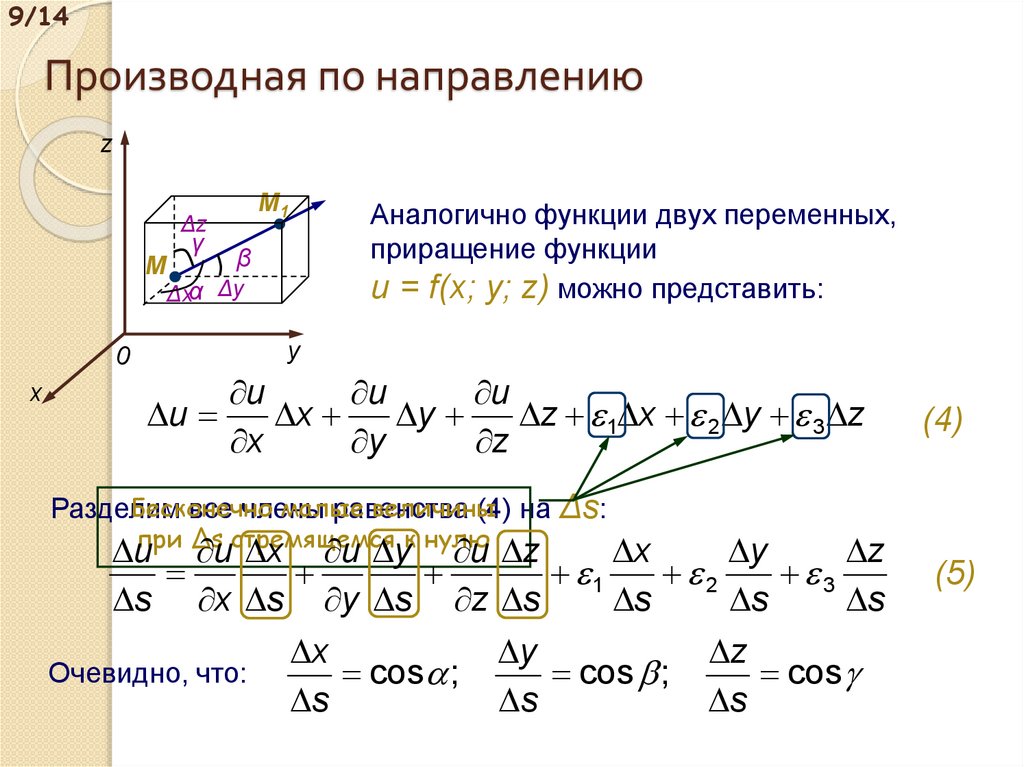
Аналогично функции двух переменных,
приращение функции
u = f(x; y; z) можно представить:
u
u
u
u
x
y
z 1 x 2 y 3 z
x
y
z
(4)
Бесконечно
малые
величины
Разделим
все члены
равенства
(4) на Δs:
uпри Δs
uстремящемся
x u yк нулю
u z
x
y
z
1
2
3
s x s y s z s
s
s
s
x
y
z
Очевидно, что:
cos ;
cos ;
cos
s
s
s
(5)

10.

10/14
Производная по направлению
u
Предел отношения
при стремлении Δs к нулю называется
s
производной от функции u = f(x; y; z) в точке (x; y; z) по
u
u
направлении вектора s и обозначается:
lim
s s 0 s
Таким образом, переходя к пределу в равенстве (5), получим:
u u
u
u
(6)
cos
cos
cos
s x
y
z
Производная по направлению s характеризует скорость изменения
функции (поля) в точке М.
u
Если
0 функция возрастает
убывает
в направлении s
s u
Величина
представляет собой мгновенную скорость
s изменения функции в направлении s

11.

11/14
Производная по направлению
u x2 y 3 z
Дана функция
Найти производную от функции u в точке М(1; 1; 1) по направлению
вектора
s 2i 3 j k
s 22 12 32 14
1
cos
14
Находим направляющие косинусы вектора s:
cos
2
14
3
14
cos
Найдем частные производные в точке М:
u
1
z
u
3y 2 (1;1;1) 3
y
u
2 x (1;1;1) 2
x
По формуле (6) получим:
u
s
14
14
14

12.

12/14
Градиент
u
В каком направлении
имеет наибольшее значение?
s
Это направление указывает вектор, который называется градиентом
скалярного поля.
Можно заметить, что правая часть равенства (6) представляет собой
скалярное произведение единичного вектора
u u u
e cos ; cos ; cos и некоторого вектора g ; ;
x y z
Вектор, координатами которого являются значения частных
производных функции u = f(x; y; z) в точке (x; y; z) , называют
градиентом функции и обозначают:
u
u
u
grad u
i
j
k
x
y
z

13.

13/14
Градиент
Отметим, что grad u есть векторная величина. Говорят, что скалярное
поле U порождает векторное поле градиента. Теперь равенство (6)
можно записать так:
u
e grad u
s
grad u
φ
е
u
s
s
(7)
или
u
grad u cos
s
(8)
Из
формулы
(8) следует, что
производная по
угол
между направлением
градиента
направлению
достигаетs наибольшего значения,
и вектором
когда cos φ = 1, то есть при φ = 0
Таким образом, градиент указывает направление
наибыстрейшего возрастания функции. В этом
состоит физический смысл градиента.
Наибольшая скорость изменения функции U в точке M равна:
2
2
u u u
grad u
x y z
2
(9)

14.

14/14
Градиент
Найти наибольшую скорость возрастания функции в точке A(-1; 1; -1)
x y z
u
y z x
Найдем частные производные в точке А:
u 1 z
2 ( 1;1; 1) 2
x y x
u
x 1
2 ( 1;1; 1) 0
y
y
z
u
y 1
2 ( 1;1; 1) 2
z
z
x
Градиент в точке А равен: grad u
i
j
k
Наибольшая скорость возрастания функции равна:
grad u 22 02 2 2 2
2
Отметим, что функция будет убывать с наибольшей скоростью,
если точка А движется в направлении – grad u ={-2; 0; 2} –
антиградиентное направление