Похожие презентации:
Дифференциальное исчисление функции нескольких переменных
1.
ДИФФЕРЕНЦИАЛЬНОЕИСЧИСЛЕНИЕ
ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
2.
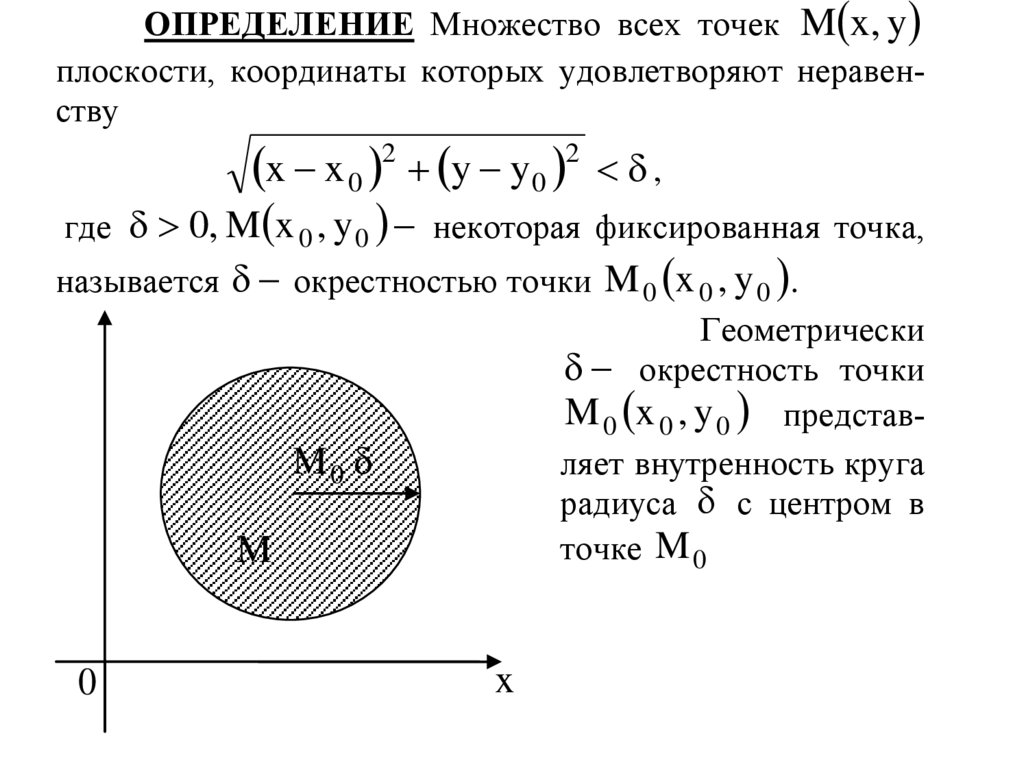
ОПРЕДЕЛЕНИЕ Множество всех точек M x, yплоскости, координаты которых удовлетворяют неравенству
x x 0 y y 0 ,
где 0, M x 0 , y 0 некоторая фиксированная точка,
называется окрестностью точки M 0 x 0 , y 0 .
2
2
Геометрически
окрестность точки
M 0 x 0 , y 0 представляет внутренность круга
радиуса с центром в
точке M 0
M0
M
0
x
3.
ОПРЕДЕЛЕНИЕ Точка M1 x 1 , y1 называется внутренней точкойнекоторого множества D , если существует окрестность этой точки, состоящая целиком из точек данного множества.
ОПРЕДЕЛЕНИЕ Множество D , состоящее лишь из внутренних точек,
называется открытым множеством.
y
y
M 2
M1
Г
D
D D Г
x
0
Рис. 1.2
x
0
Рис. 1.3
4.
ОПРЕДЕЛЕНИЕ Точка M 2 x 2 , y 2 называется граничной точкой множества D , если влюбой ее окрестности есть точки, как принадлежащие множеству D , так и не принадлежащие
ему. Множество всех граничных точек данного
множества D называется границей этого
множества.
ОПРЕДЕЛЕНИЕ Множество точек плоскости называется линейно-связным, если любые
две точки этого множества можно соединить непрерывной линией, состоящей из точек этого же
множества.
5.
ОПРЕДЕЛЕНИЕ Линейно-связноеоткрытое множество точек плоскости называется областью.
Простейшими областями являются:
внутренность круга, эллипса, треугольника
и т.п.
ОПРЕДЕЛЕНИЕ Множество точек
плоскости, образованное областью и ее
границей, называется замкнутой областью.
ОПРЕДЕЛЕНИЕ Область называется ограниченной, если существует круг,
внутри которого она содержится.
6.
ОПРЕДЕЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХПЕРЕМЕННЫХ
Пусть даны два числовых множества D и E , где D
2
некоторая область из пространства R , а E некоторое
подмножество множества R .
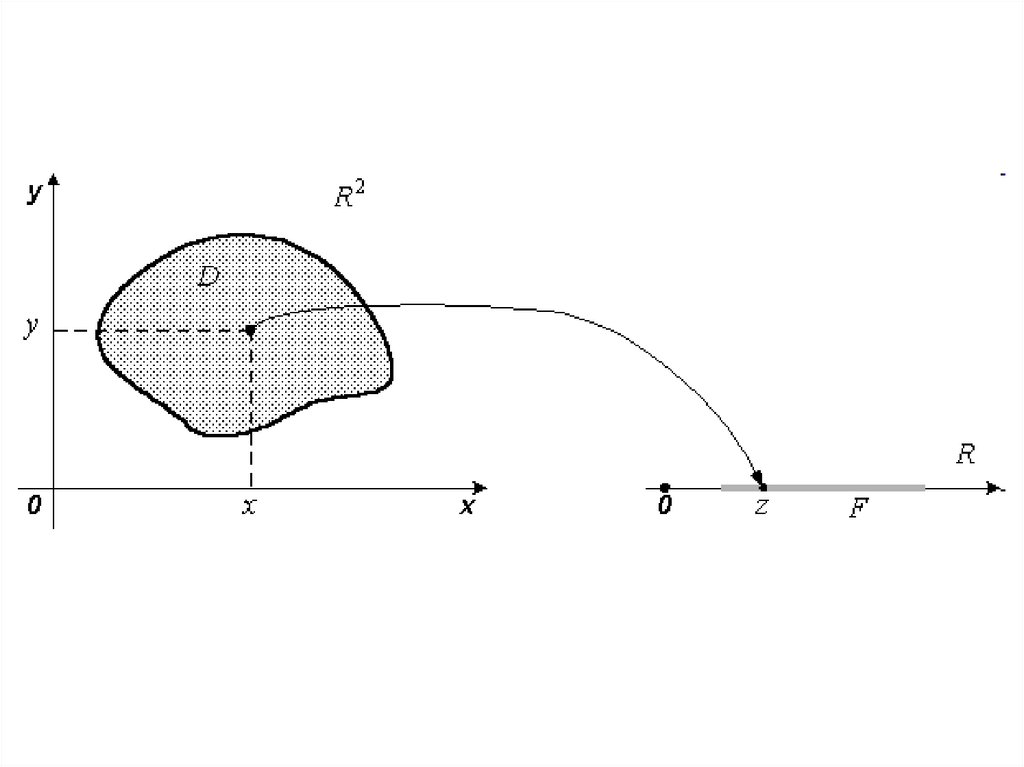
ОПРЕДЕЛЕНИЕ Если каждой паре чисел x , y D
по некоторому правилу (закону) поставлено в соответствие
единственное число z E , то говорят, что на множестве D
задана функция двух переменных z f x , y .
При этом x и y называются независимыми переменными (или аргументами), z зависимой переменной (или
функцией), множество D областью определения функции, а E множеством значений функции.
7.
8.
9.
Так как каждой паре чисел x , y при фиксированной системе координат соответствуетединственная точка M x , y плоскости и,
обратно, каждой точке M x, y соответствует
пара чисел x , y , то функцию двух переменных можно рассматривать как функцию
точки M x , y и вместо записи z f x , y
писать z f M , а областью определения
функции в этом случае будет некоторое множество точек плоскости.
10.
11.
x y2
2
f ( x y ) sin
exp x y
5
f
12.
f13.
ПРИМЕР Найти область определения и С-уровни функции, заданнойформулой
u
2y
.
2
2
x y 1
Решение. Функция определена в тех и только тех точках (x; y) плоскости, координаты которых удовлетворяют неравенству
2y
0.
2
2
x y 1
Это неравенство равносильно двум системам неравенств:
y 0,
и
2
2
x y 1
y 0,
2
2
x
y
1.
Первой системе неравенств удовлетворяют координаты всех точек, расположенных в полуплоскости y 0 и вне окружности радиуса R=1 с центром в начале координат. Второй системе удовлетворяют все точки плоскости, лежащие
в полуплоскости y 0 и внутри окружности радиуса R=1 с центром в начале
координат. На рисунке область определения функции показана штриховкой.
14.
y1
0
1
x
15.
ПРИМЕР Найти область определения функцииu x 2 y 2 1 ln 4 x 2 y 2 .
Решение. Область определения дано функции находится из решения системы
2
2
x y 1 0;
2
2
4
x
y
0;
1 x 2 y2 4
y
D
0
Рис.2.4
1
2 x
16.
ПРИМЕР Найти область определения функции2 2
u y x y2 .
3
Решение.
Функция определена при условии
x 2 y 2 0 , или x 2 y 2 . Отсюда граница области определения
D
определяется
из
уравнения
2
2
x y x y . Для внутренних точек области D
должно выполняться неравенство x y x y .
Таким образом, область D состоит из всех точек двух
углов между биссектрисами x y , включая в себя
обе свои границы.
2
2
17.
yD
D
0
x
18.
ПРИМЕР Найти область определения функцииx 2 y2 z2
u 1 2 2 2 .
a
b
c
Решение. Область определения V данной функции определяется условием
x 2 y2 z2
x 2 y2 z2
1 2 2 2 0 2 2 2 1.
a
b
c
a
b
c
x 2 y2 z2
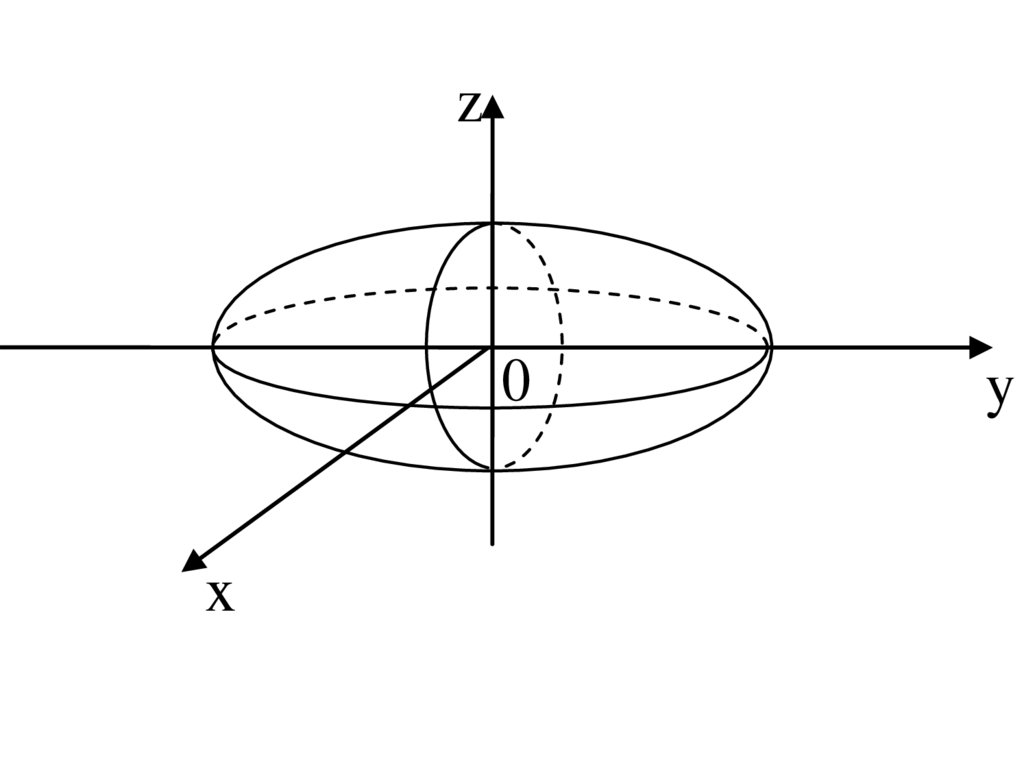
Ее граница 2 2 2 1 есть поверхность эллипсоида с
a
b
c
полуосями a, b и c. Так как т.О (0,0,0), лежащая внутри эллипсоида, удовлетворяет указанному выше неравенству, то
область V состоит из внутренних точек эллипсоида. Эта область замкнута, так как включает в себя и границу.
19.
z0
x
Рис. 2.5
y
20.
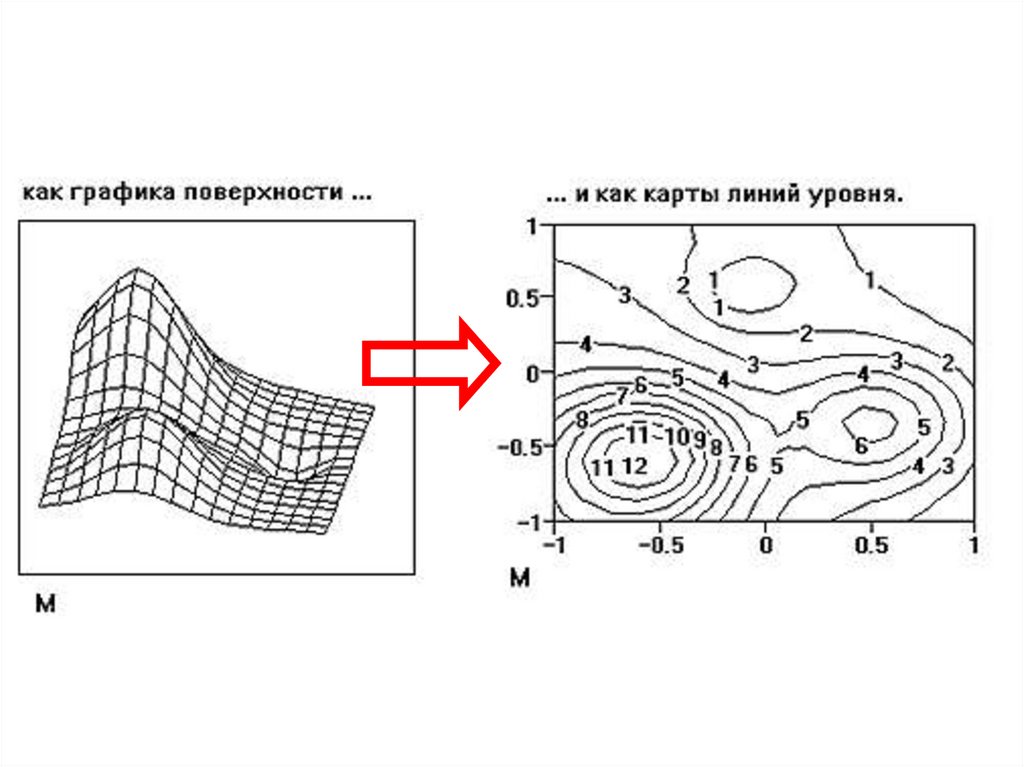
ОПРЕДЕЛЕНИЕЛинией
уровня функции z f x , y называет-
ся множество точек x; y плоскости
Oxy , в которых функция принимает
одно и то же значение c .
Очевидно, давая c различные
значения, мы будем получать различные линии уровня для данной функции.
21.
zy
x
с1
с2
с
с3 4
22.
ПРИМЕР. Построить линии уровня функции2
2
z x y .
Решение. Для того чтобы найти линии уровня
данной
функции,
пересечем
поверхность
2
2
z x y
плоскостью
z c . Получаем
x y c
2
2
0 c . Задавая c различ-
ные значения, например, c 0,1,2,..., получим
семейство линий уровней, представляющих собой
окружность. При C 0 окружность вырождается в
точку 0;0 .
23.
4y
с3
с2
y
c1
x
24.
25.
26.
27.
ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИНЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Пусть функция u f M определена в некоторой ок-
0
0
0
рестности точки M 0 x1 , x 2 ,..., x n , за исключением, быть
может, самой точки M 0 .
ОПРЕДЕЛЕНИЕ Число A называется пределом функции
z f M при M M 0 , если для любого числа 0
найдется такая окрестность точки M 0 , что для любой
точки M из этой окрестности (за исключением, быть может,
точки M 0 ) имеет место неравенство
f M A .
28.
При этом пишут lim f M A илиM M 0
lim f x 1 , x 2 ,..., x n A , так как при
x1 x10
x 2 x 02
x n x 0n
M x1 , x 2 ,..., x n M 0 x , x ,..., x ,
0
1
очевидно x 1 x
0
1,
x2 x
0
2
0
n
0
2 ,...,
xn x
0
n.
29.
ПРИМЕР Найти limx 0
y 0
x2 y2
x y 1 1
2
2
.
Решение.
Предел
функции
находится
при
M x; y M 0 0;0 , т.е. при 0 , где M 0 M расстояние
между точками M 0 и M . В данном случае
разом,
lim
M M 0
x y
2
2
x y 1 1
2
2
lim 2 1 1 2 .
0
lim
0
x 2 y 2 . Таким об-
2
2
1 1
lim
2
2
1 1 0 1 1
2
30.
x 2yПРИМЕР Вычислить предел lim 2
.
2
x x 2 xy 2 y
y
Решение. Перейдем к полярным координатам:
x cos , y sin .
x 2y
1
cos 2 sin
1 f
Тогда 2
,
2
2
2
cos 2 cos sin 2 sin g
x 2xy 2 y
а условие M x, y эквивалентно условию .
1
При первый сомножитель
стремится к нулю. Второй со
f
множитель
при 0 2 ограничен. Произведение бескоg
нечно-малой функции на ограниченную функцию есть бесконечно
малая функция, поэтому искомый предел равен нулю.
31.
x2 y2ПРИМЕР Найти предел lim 2
.
x 0 x y 2
y 0
x2 y2
Решение. Функция z 2
определена на всей плоско2
x y
сти, за исключением начала координат.
Приближаясь к началу координат по оси Ox , где y 0 по-
x2 0
1.
лучим lim 2
x 0 x 0
Если же приближаться к началу координат по оси Oy , где
0 y
1.
x 0 , то lim
y 0 0 y 2
Таким образом, при приближении точки M x , y к началу
координат по различным направлениям функция имеет различные
предельные значения и, следовательно, не имеет предела при
x 0, y 0.
32.
ОПРЕДЕЛЕНИЕ Функция u f M называется непрерывной в точке M 0 , если она определена в точке M 0 и некоторой ее окрестности иlim f M f M 0 .
M M 0
Точка M 0 , в которой функция нескольких
переменных u f M непрерывна, называется
точкой непрерывности этой функции.
Точки, в которых функция не является непрерывной, называются точками разрыва этой
функции.
33.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИНЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Рассмотрим
функцию
двух
переменных
z f x , y . Зафиксируем значения аргумента y и переменной x дадим произвольное приращение. Тогда
функция получит соответствующее приращение
x z f x x , y f x , y ,
которое называется частным приращением функции
по переменной x в точке M x , y .
Аналогично определяется частное приращение
функции по переменной y
y z f x, y y f x, y
34.
ОПРЕДЕЛЕНИЕ Частной производной функции z f x , y по переменной x , в точке M x , y называется предел (если таковой существует) отношениячастного приращения x z к приращению аргумента x
при стремлении последнего к нулю:
f x x, y f x, y
xz
z
lim
lim
x x 0 x x 0
x
Аналогично определяется частная производная
yz
f x, y y f x, y
z
lim
lim
y y 0 y y 0
y
35.
Для обозначения частных производных функции двух переменных применяются следующие символы:f z
z x , f x x , y , ,
x x
f z
z y , f y x , y , , .
y y
36.
ПРИМЕР Найти значения частных производныхфункции
3
2
3
в точке
u 2x 3x y 6xy y
M 0 1,2 .
Решение. Считая y постоянной и
дифференцируя u, как функцию x, находим частную производную по x, вычисляем ее значение в точке M 0 :
u
2
6 x xy y ;
x
u
2
M 0 6 1 2 2 6 .
x
37.
Считая x постоянной и дифференцируя u, как функцию y, находимчастную производную по y, вычисляем ее значение в точке M 0 :
u
2
2
3 x 2x y ;
y
u
2
2
M 0 3 1 2 2 15 .
y
38.
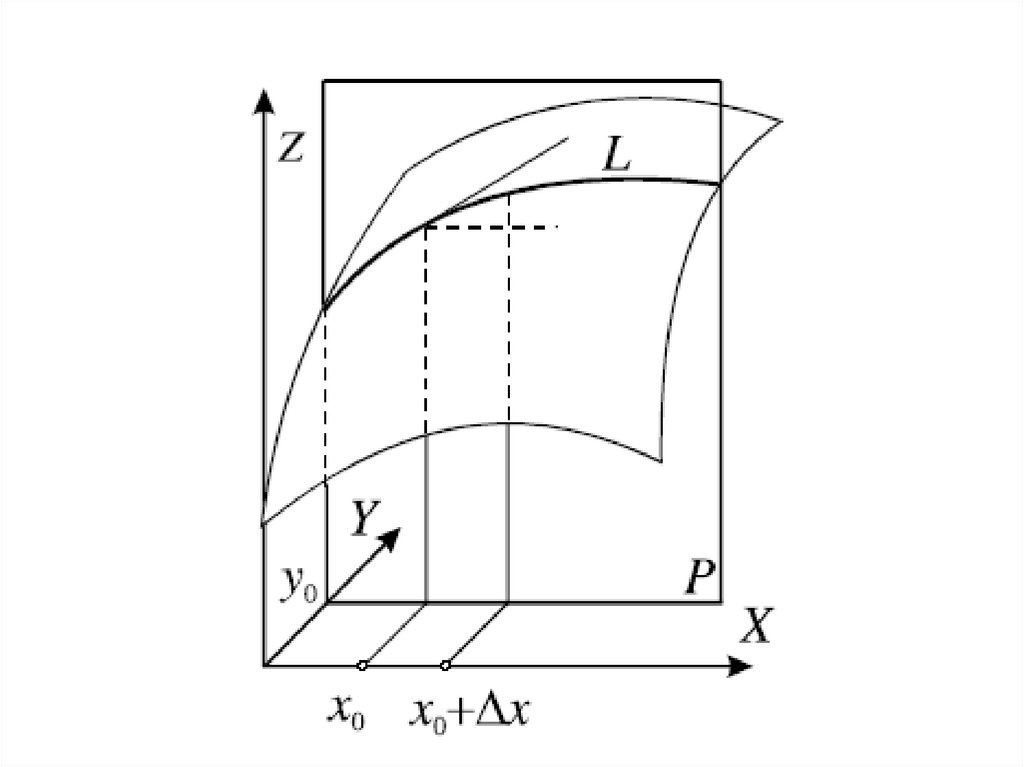
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ЧАСТНЫХПРОИЗВОДНЫХ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Пусть функция z f x , y имеет частные производные
в точке M 0 x 0 , y 0 . Как известно, графиком данной функции
является некоторая поверхность
Полагая y y 0 const и рассматривая систему урав-
z f x , y
нений
, мы получаем плоскую кривую AP0 B ,
y y0
представляющую собой сечение поверхности z f x , y
плоскостью y y 0 , параллельной координатной плоскости
Oxz .
39.
40.
41.
Согласно геометрическому смыслу производнойdf x , y 0
tg , где
функции одной переменной,
dx
угол образованный с осью Ox касательной, проведенной к
кривой AP0 B в точке P0 . С другой стороны
df x, y 0
f x 0 x , y 0 f x 0 , y 0 z
lim
.
x 0
x x
dx
x
x
x x
y y
0
0
z
tg .
Отсюда следует,
x
0
42.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВПусть имеем некоторую функцию z f x , y от
двух переменных x и y .
Ее
частные
производные
z
f x x , y
x
и
z
f y x , y являются функциями от переменных x и y .
y
2
2
z z
z
z
f xx x , y ,
f xy x , y ,
2
x
x x
x y y x
2 z
z
2 z z
f yx x, y ,
f yy x, y .
2
y x x y
y
y y
43.
ПРИМЕР Пусть z tg (3x y) .Имеем
z
3
2z
3
3x y sin(3x y) ,
,
18
cos
2
2
x cos (3x y)
x
z
1
,
2
y cos (3x y)
6 sin(3x y) ,
2z
x y
cos 3 (3x y)
2 z 6 sin(3x y) .
y x
cos 3 (3x y)
2z
y
3
,
2
cos
(
3
x
y
)
sin(
3
x
y
)
2
44.
Теорема Если в некоторой окрестности точки M x , y производныеf xy x, y и f yx x, y существуют и непрерывны в самой точке M x , y , то они
равны между собой в этой точке, т.е.
имеет место равенство:
f xy x, y f yx x, y .
45.
ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИНЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Пусть
дана
функция
двух
переменных
z f x , y . Предположим, что ее аргументы x и y получают соответственно приращения x и y . Тогда
функция получает полное приращение, которое определяется формулой
z f x x , y y f x , y
Геометрически полное приращение z равно
приращению аппликаты графика функции z f x , y
при
переходе
из
M 1 x x , y y
точки
M x , y
в
точку
46.
ОПРЕДЕЛЕНИЕ Функция z f x , y называетсядифференцируемой в точке M x , y , если ее полное приращение в этой точке может быть представлено в виде
z A x B y x, y x x, y y ,
где
ла, а
A и B некоторые не зависящие от x и y чис-
x , y и x , y бесконечно малые при
x 0, y 0 функции.
47.
Теорема Если функция z f x , y диффе-ренцируема в точке M x , y , то она непрерывна
в этой точке.
Теорема Если функция z f x , y диффе-
ренцируема в точке M x , y , то она имеет в этой
точке
частные
f y x, y B.
производные
f x x , y A ,
48.
ТеоремаЕсли функция
z f x , y имеет частные производные в некоторой окрестности
точки M x , y и эти производные
непрерывны в самой точке, то эта
функция дифференцируема в
точке M x , y .
49.
ПРОИЗВОДНЫЕ СЛОЖНОЙФУНКЦИИ
Теорема Если функции x x t и
y y t дифференцируемы в точке t , а
функция z f x , y дифференцируема в
соответствующей точке M x t , y t , то
сложная функция z f x t , y t также
дифференцируема в точке t и имеет место
формула
dz z dx z dy
dt x dt y dt
50.
Рассмотрим частный случай, когда z f x , y , где y x . Тогдаz f x, x
является
функцией переменной x
сложной
dz z dx z dy
dx x dx y dx
или
dz z z dy
.
dx x y dx
51.
u f x , y , z ,где
x x t , y y t , z z t , то
Если
du u dx u dy u dz
.
dt x dt y dt z dt
52.
x x u, , y y u,дифференцируемы в точке P u, , а функция
z f x , y дифференцируема в точке M x , y ,
где x x u, , y y u, , то сложная функция z f x u, , y u, дифференцируема в
точке P u, ,
Если
функции
z z x z y
,
u x u y u
z z x z y
.
x y
53.
uПРИМЕР Пусть z x y , x u , y
z
2 3
3 2 1
3x y 3x y ;
u
.
z
u
2 3
3 2
3x y u 3x y 2
3
3
54.
ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИНЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ОПРЕДЕЛЕНИЕ Полным дифференциалом dz
M x , y функции
дифференцируемой в точке
z f x , y называется главная линейная относительно приращений x и y часть полного приращения
этой функции в точке M x , y , т.е.
dz fx x, y x fy x, y y .
55.
При достаточно малых x и y можно принятьz dz или
f x x, y y
f x, y f x x, y x f y x, y y
.
56.
ноПРИМЕР Вычислить приближенс
помощью
дифференциала
1,97
arctg
1 .
1,02
Решение. Рассмотрим функцию
x
f x , y arctg 1 .
y
57.
x xx
arctg
1 arctg 1
y y
y
x
x
arctg 1 x arctg 1 y
y
y
y
x
x x
x
arctg
1 arctg 1
y y
y
или
y
x
2
x 2
y
2
2
y x y
y x y
.
58.
Положимтеперь
x 2, y 1 ;
x 0,03, y 0,02 . Следовательно
тогда
2 0,03
2
arctg
1 arctg 1
1
1 0,02
1
2
2
0,03 2
0,02
2
2
1 2 1
1 2 1
Или
1
1,97
arctg
1 arctg1 0,03 0,02 0,75 .
1,02
2
59.
ОПРЕДЕЛЕНИЕ Плоскость, проходящая через точку N 0 , называется касательной плоскостью к поверхности в точке N 0 , если угол междусекущей N 0 N и этой плоскостью стремится к нулю, когда расстояние
N 0 N стремится к нулю, каким бы образом точка N на поверхности ни
стремилась к точке N 0 .
N0
N
Рис. 1.7
60.
61.
ОПРЕДЕЛЕНИЕ Нормалью к поверхности вточке N 0 называется прямая, проходящая через точку
N 0 перпендикулярно касательной плоскости к поверхности в этой точке.
Уравнение касательной плоскости к поверхности z f x , y в точке N 0 x 0 , y 0 , z0 имеет вид
z z 0 f x x 0 , y 0 x x 0 f y x 0 , y 0 y y 0 ,
а нормаль к поверхности в точке N 0 определяется
уравнением
x x0
y y0
z z0
.
f x x 0 , y 0 f y x 0 , y 0
1
62.
Теорема (существования неявной функции)Если функция F x , y и ее частные производ-
ные Fx x , y и Fy x, y определены и непрерывны
в некоторой окрестности точки M 0 x 0 , y 0 и при
этом F x 0 , y 0 0, а Fy x 0 , y 0 0 , то уравнение
F x , y 0 определяет в окрестности точки
M 0 x 0 , y 0 единственную неявную функцию
y x , непрерывную и дифференцируемую в
некотором интервале, содержащем точку x 0 , причем
x 0 y 0 .
63.
Fdy
x
F
dx
y
64.
ПРИМЕР Найти производнуюнеявной функции y , заданной
уравнением
x 2 x 3y xy 1 0 ,
2
2
и вычислить ее значение в точке
P 2; 1 .
65.
Решение.Введем
обозначение
F x, y x 2x 3y xy 1.
F
F
2 x 2 y;
6y x .
Тогда
x
y
2
Следовательно,
2
dy
2x 2 y
и
dx
6y x
dy
2 2 2 1 1
.
dx xy 21
6 1 2 4
66.
Рассмотрим уравнение видаF x , y , z 0 .
F
F
z
z
y
x
Тогда
,
F
F y
x
z
z
67.
Предположим, что к поверхности, заданной уравнением F x , y , z 0 , в точке P0 x 0 , y 0 , z 0 можнопровести касательную плоскость.
Тогда уравнение этой плоскости можно по формуле
Fx P0 x x 0 Fy P0 y y 0 Fz P0 z z 0 0 .
Уравнение нормали в точке P0 x 0 , y 0 , z 0 запишется в виде
x x 0 y y 0 z z0
.
Fx P0 Fy P0 Fz P0
68.
ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХПусть функция z f x , y задана в некоторой об-
ласти D и M 0 x 0 , y 0 некоторая точка из этой области.
ОПРЕДЕЛЕНИЕ Функция z f x , y имеет в
точке M 0 x 0 , y 0 максимум (минимум), если существует такая окрестность этой точки, что для всех точек
M x, y этой окрестности, отличных от M 0 x 0 , y 0
выполняется неравенство
f M 0 f M
f M 0 f M .
69.
70.
ОПРЕДЕЛЕНИЕ Точки, в которыхчастные производные первого порядка
f x x , y и f y x, y обращаются в нуль
или не существуют называются критическими
точками
функции
z f x , y .
71.
Теорема Пусть в некоторой области, содержащей критическую точку M 0 x 0 , y 0 функция z f x , y имеет непрерывныечастные производные до второго порядка включительно. Положим
f xx x 0 , y 0 f xy x 0 , y 0
.
f xy x 0 , y 0 f yy x 0 , y 0
Тогда:
1) если 0 , то в точке M 0 x 0 , y 0 функция имеет экстремум, причем
при f xx
x 0 , y 0 0 максимум,
при f xx
x 0 , y 0 0 минимум;
2) если 0 , то в точке M 0 x 0 , y 0 нет экстремума;
3) если 0 , то точка M 0 x 0 , y 0 может быть, а может и
не быть точкой экстремума (в этом случае необходимы
дополнительные исследования).
72.
ПРИМЕР Исследовать на экстремум функциюz x 3 3xy 2 30x 18y .
Решение. Областью определения является вся плоскость
Найдем
критические
точки.
R2 .
2
2
f x x, y 3x 3y 30, f y x, y 6xy 18 .
Приравнивая эти производные нулю, приходим к системе:
x 2 y 2 10
x 2 2 xy y 2 16
x y 4
2
2
x y 2
x 2 xy y 4
2 xy 6
73.
Решая эту систему уравнений, находим четырекритические точки
M 1 3;1 , M 2 1;3 ,
.
M 3 1; 3 , M 4 3; 1
Теперь найдем вторые частные производные:
fxx x, y 6x, fxy x, y 6y, fyy 6x
и составим выражение
36 x y .
M f xx M f yy M f xy M
2
2
2
74.
Тогда:M 1 288 0, f xx M 1 18 0,
точка
1)
M 1 3;1
минимума;
2) M 2 288 0, в точке M 2 1;3
экстремума нет;
точке
в
3) M 3 288 0 ,
M 3 1; 3 экстремума нет;
4) M 4 288 0, f xx
M 4 18 0,
M 4 3; 1 точка максимума.
75.
Итак, данная функция имеет два экстремума:в точке M1 минимум,
f M1 72
и в точке M 4 максимум,
f M 4 72.
76.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕЗНАЧЕНИЕ ФУНКЦИИ ДВУХ
ПЕРЕМЕННЫХ
Для того чтобы найти наибольшее и наименьшее значения функции z f x , y в ограниченной замкнутой области D , следует найти
значения функции в критических точках этой области, а также ее наибольшее и наименьшее значения на границе области D .
Наибольшее и наименьшее из всех этих значений являются соответственно наибольшим и
наименьшим значениями функции z f x , y в заданной области D .
77.
ПРИМЕР Найти наибольшее и наименьшее2
2
z x y
значения функции
в круге
x y 4.
2
2
Решение. Находим z x 2x и z y 2 y . Решая
2x 0
систему уравнений
получим одну
2y 0
критическую точку M 0 0;0 , в которой значение функции равно нулю.
78.
Найдем теперь наибольшее и наименьшеезначения функции на границе, т.е. на ок2
2
ружности x y 4 .
Для точек этой окружности функцию
2
2
z x y можно представить как функцию
одной
переменной
x:
2
2
2
z x 4 x , т.е. z 2x 4 , при-
чем 2 x 2 .
79.
Нахождение наибольшего и наименьшего значений функции двухпеременных
на
окружности
2
2
x y 4 свелось к нахождению
наибольшего и наименьшего значений функции одной переменной
2
z 2x 4 на отрезке 2;2 .
80.
Найдем критические точки этойфункции на интервале 2;2 и вычислим значения функции в этих
точках и на концах отрезка.
Имеем z 4x, 4x 0 , откуда получаем
критическую
точку
x 0; z x 0 4 .
81.
Далее,находим
z x 2 4 .
Таким
z x 2 4 ,
образом,
функция
2
z 2x 4 имеет наибольшее
значение, равное 4 , и наименьшее значение, равное
4.
82.
Итак, наибольшее значение функ22
z x y
ция
в
круге
x y 4 принимает в точках
M 1 2;0 и M 2 2;0 окружно2
2
сти x y 4 и наименьшее - в
точках M 3 0;2 и M 4 0; 2 той
2
2
же окружности.
83.
Алгоритм нахождения условного экстремума функции u f x, y при условии связиx,y 0
методом неопределенных множителей
Лагранжа
1). Составить функцию Лагранжа
x, y, , f x, y x, y .
2).
Найти
частные
x, y , x, y ,
,
.
x
y
(1)
производные
84.
3). Решить систему уравнений:x
,
y
,
0
,
x
x, y, 0,
y
x , y 0.
Пусть x 0 , y 0 , 0 решение данной
системы.
85.
4). Найти второй дифференциал функцииЛагранжа
2
2
d
dx 2
d xd y
dy ,
2
2
x y
x
y
2
2
2
2
при условии, что dx и dy связаны соотношением dy( x , y) 0 , т.е.:
x, y
x, y
dx
dy 0 . (3)
x
y
86.
5). Подставить в (2) значенияx x 0 , y y 0 , 0 и выражение dy из (3).
Если d 0 , то функция
f (x, y) имеет условный максимум;
2
а если d 0 , то функция f ( x, y)
имеет условный минимум.
2
87.
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮОПРЕДЕЛЕНИЕ
Производной
функции u u x , y , z в точке M x , y , z
по направлению вектора a называется предел
au
lim
.
a 0 a
88.
u uu
u
cos cos cos
a x
y
z
89.
ПРИМЕРНайти производную функции
u xy yz 1 по направлению вектора
a 12; 3; 4 в точке M 0; 2; 1 .
Решение. Найдем частные производные функции u xy yz 1 :
u
u
u
y;
x z;
y.
x
y
z
Эти производные в точке M 0; 2; 1
имеют значения:
u
u
u
2;
1;
2 .
x M
y M
z M
90.
Теперь найдем направляющие косинусы вектора a :a 12 3 4 13;
2
12
cos ;
13
3
cos
;
13
4
.
cos
13
2
2
91.
После этого, вычисляем производнуюu
12
3
4
2 1
2
a M
13
13
13
24 3 8
1
13
.
92.
ГРАДИЕНТОПРЕДЕЛЕНИЕ Вектор, координатами которого являются частные производные
первого порядка функции u u x , y , z в точке M x , y , z , называется градиентом данной
функции и обозначается:
u
u
u
grad u
i j k.
x
y
z
u u u
grad u ; ; .
x y z
93.
Теорема. Пусть в некоторой области3
D R задана дифференцируемая функция
u u x , y , z , для которой в каждой точке
области
существует
D
u u u
grad u ; ; .
x y z
Тогда
производная
функции
по направлению вектора
u u x , y , z
a a 1 , a 2 , a 3 есть
grad u на вектор a .
проекция
вектора
94.
Следствие 1 Из всех производныхпо направлению, вычисленных для
функции u u x , y , z в одной и
той же точке, наибольшее значение
имеет та производная, которая вычислена в направлении градиента.
95.
Следствие 2 Производная по направлению вектора, перпендикулярного к векторуgrad u , равна нулю.
96.
Теорема Для функции двух переменных u u x , y вектор grad uнаправлен перпендикулярно к касательной, проведенной к линии уровня
u x , y c в точке M x , y .
Теорема
Градиент функции
трех переменных u u x , y , z направлен по нормали к поверхности
уровня, проходящей через данную
точку.




































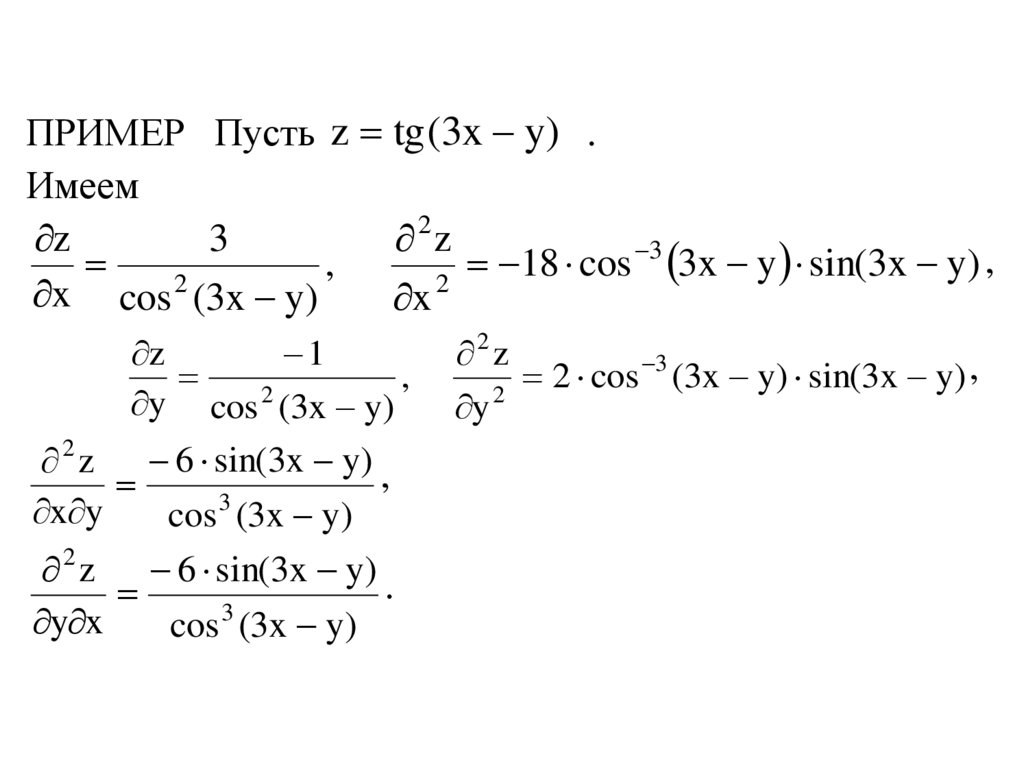













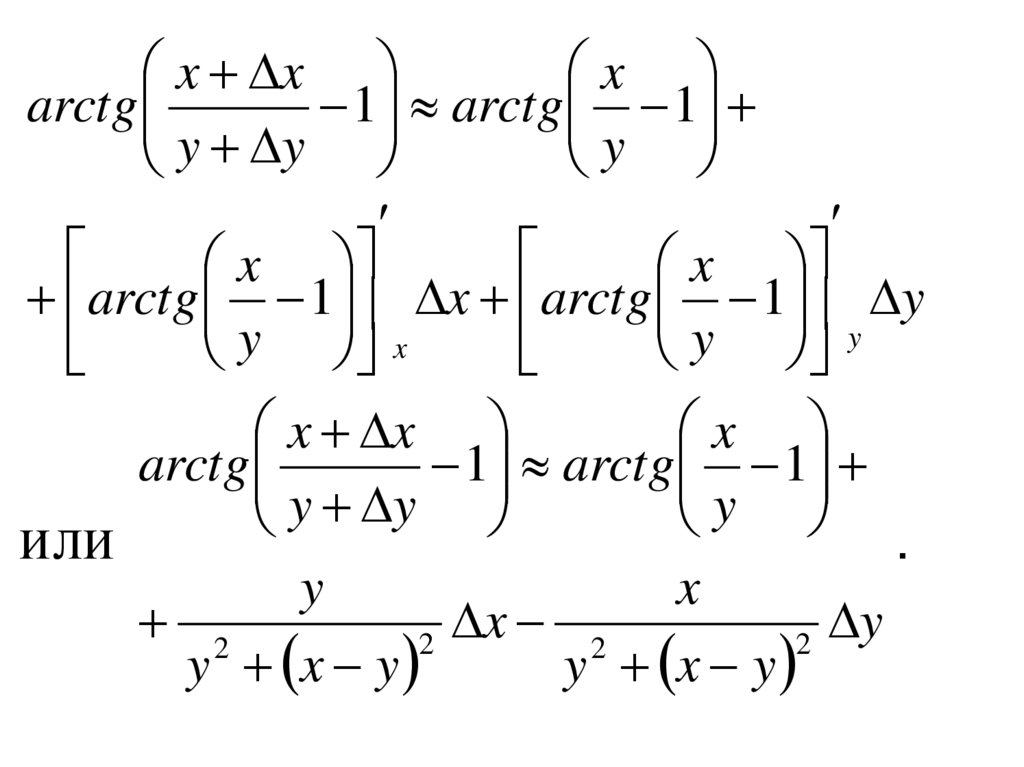






































 Математика
Математика








