Похожие презентации:
Равносильные преобразования
1.
Равносильныепреобразования.
2.
Равносильныепреобразования
Определение 1. Две формулы алгебры
логики А и В называются равносильными,
если они принимают одинаковые
логические значения на любом наборе
значений входящих в них высказываний
(А
В)
3.
1. Основные равносильности1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
- законы
идемпотентности
- закон
противоречия
- закон исключенного третьего
- закон снятия двойного отрицания
- законы поглощения
4.
II. Равносильности, выражающие одни логическиеоперации через другие:
1.
2.
3.
4.
5.
6.
Законы де
Моргана
5.
III. Равносильности, выражающие основныезаконы алгебры логики:
- коммутативность конъюнкции.
- коммутативность дизъюнкции.
- ассоциативность конъюнкции.
- ассоциативность дизъюнкции.
- дистрибутивность конъюнкции
относительно дизъюнкции.
6.
- дистрибутивность дизъюнкции
относительно конъюнкции.
1.
2.
3.
4.
5.
6.
Используя равносильности группы I, II и III, можночасть формул алгебры логики или всю формулу
заменить равносильной ей формулой.
Такие преобразования
называются равносильными.
Равносильные преобразования формул
применяются для
доказательства равносильностей, для приведения
формул к заданному виду, для упрощения
формул.
7.
Пример 1. Доказать равносильность.
Решение. Для доказательства
равносильности подвергнем ее левую
часть равносильным преобразованиям:
8.
Пример 2. Доказать тождественнуюистинность формулы:
Решение.
9.
Связь равносильностей ставтологиями
Если некоторая формула
является тавтологией, то и всякая
равносильная ей формула также
является тавтологией.
10.
Таким образом, равносильныепреобразования можно также применять
для доказательства тождественной
истинности тех или иных формул.
Для этого данную формулу нужно
равносильными преобразованиями
привести к одной из формул, которые
являются тавтологиями.
11.
Двойственные формулыДве формулы, не содержащие
знаков импликации и
эквиваленции, называются
двойственными, если каждую из
них можно получить из другой
заменой знаков соответственно
на
12.
Принцип двойственностиЕсли две формулы, не
содержащие знаков
импликации и эквиваленции,
равносильны, то и двойственные
им формулы также
равносильны.
13.
Логическое следствиеЛогическое следствие из данных
посылок есть высказывание,
которое не может быть ложным,
когда эти посылки истинны.
14.
Некоторое выражение В естьлогическое следствие из формулы А
(где А и В — обозначения для
различных по форме высказываний),
если, заменив те конкретные
элементарные высказывания, которые
входят в А и В, переменными, мы
получим тождественно-истинное
выражение (А → В), или закон логики.
15.
ПримерНам даны три посылки:
1)
«Если Иван — брат Марьи или Иван — сын
Марьи, то Иван и Марья — родственники»;
2)
«Иван и Марья — родственники»;
3)
«Иван — не сын Марьи».
Можно ли из них вывести логическое
следствие, что «Иван — брат Марьи»?
Обозначим суждение «Иван — брат Марьи»
буквой (переменной) а,
суждение «Иван — сын Марьи» — буквой b
и суждение «Иван и Марья — родственники» —
буквой с.
16.
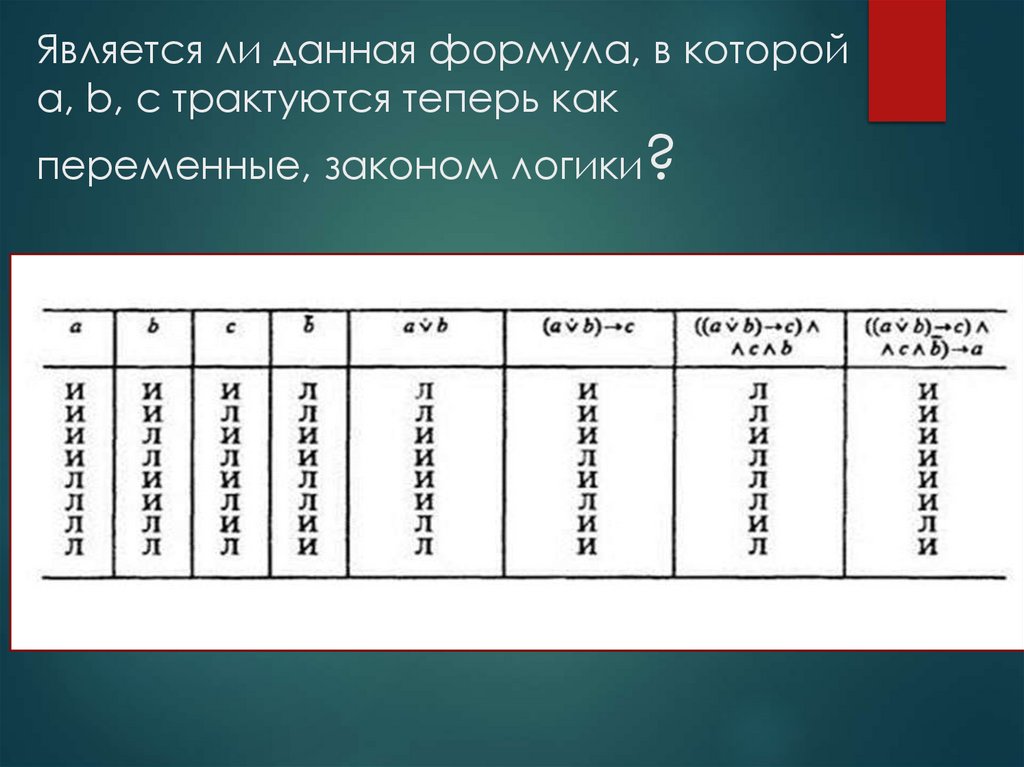
Является ли данная формула, в которойа, b, с трактуются теперь как
переменные, законом логики?
17.
В последней колонке формула водном случае принимает
значение «ложь», значит, она не
является законом логики.
Следовательно, из данных трех
посылок не следует с
необходимостью заключения, что
«Иван — брат Марьи».
Иван может быть племянником
Марьи, или отцом Марьи, или
дядей Марьи, или каким-либо
другим ее родственником.
18.
Какое число нужно поставитьвместо знака вопроса?
19.
Слово из пяти букв, с однойгласной.
С буквой "О" - это "сила", с
буквой "И" - это "могила"
СПИРТ-СПОРТ
20.
Если все решения первого уравнения являютсярешениями второго уравнения (множество
решений первого уравнения является
подмножеством решений второго уравнения), то
второе уравнение называется следствием
первого уравнения.
Обозначение:
Таким образом, два уравнения равносильны
тогда и только тогда, когда каждое из них является
следствием другого.
21.
Теоремыравносильности
Теорема 1. Если любое выражение,
входящее в уравнение, заменить
тождественно равным ему на области
определения уравнения выражением,
то получим уравнение, равносильное
данному.
22.
Теорема 2. Если к обеим частям уравненияприбавить выражение, имеющее смысл на
области определения уравнения, то получим
уравнение, равносильное данному.
Следствие. Если любое слагаемое
перенести из одной части уравнения в другую,
поменяв его знак на противоположный, то
получим уравнение, равносильное данному.
Теорема 3. Если обе части уравнения
умножить (разделить) на выражение, имеющее
смысл и отличное от нуля на области
определения уравнения, то получим уравнение,
равносильное данному.
23.
Какую картинку (А, Б, В или Г) необходимо подставитьвместо знака вопроса, чтобы закончить
последовательность?
24.
Продолжите следующуюпоследовательность букв :
С О Н Д Я Ф М ...
25.
Какое слово здесьзашифровано?
Подсказка. В надписи из букв, где все буквы
стоят вертикально, рядом с каждой буквой слева
провели вертикальную ось, и начали быстро-быстро
крутить каждую букву вокруг этих осей .
В результате со стороны это стало выглядеть так.

























 Математика
Математика








