Похожие презентации:
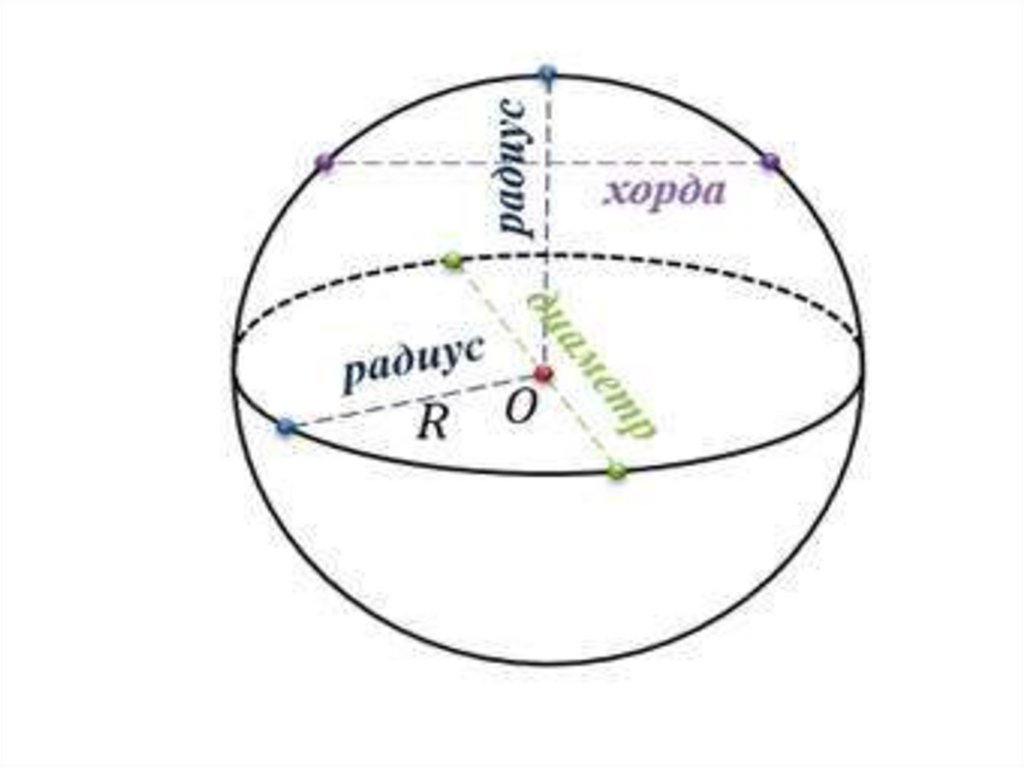
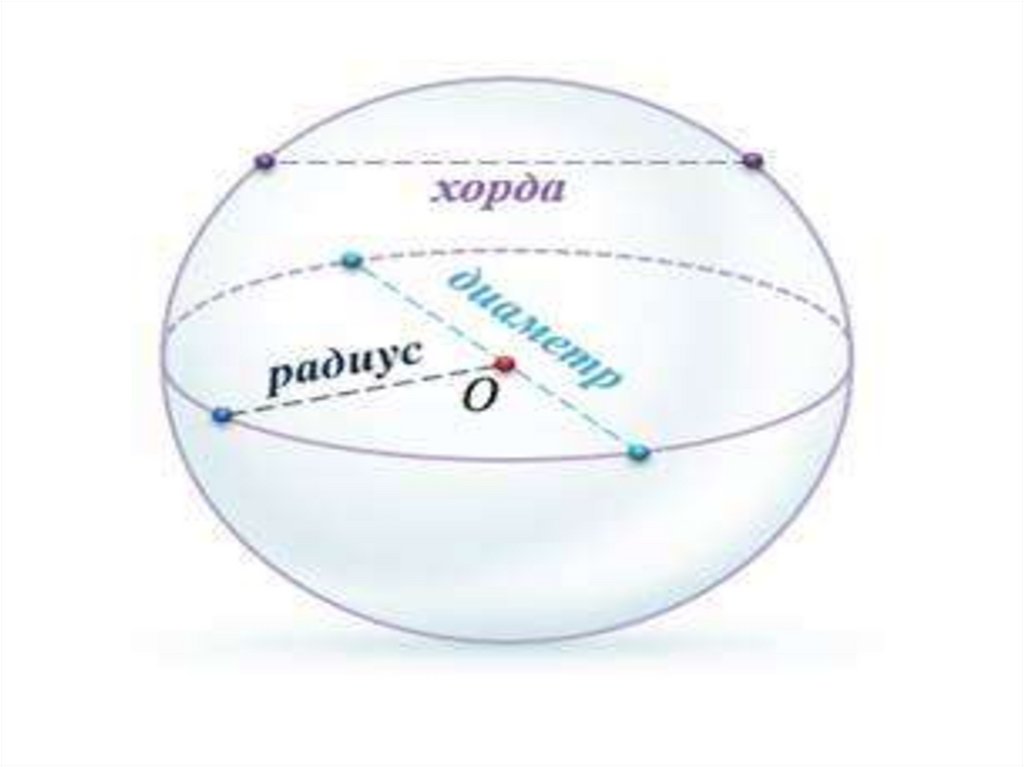
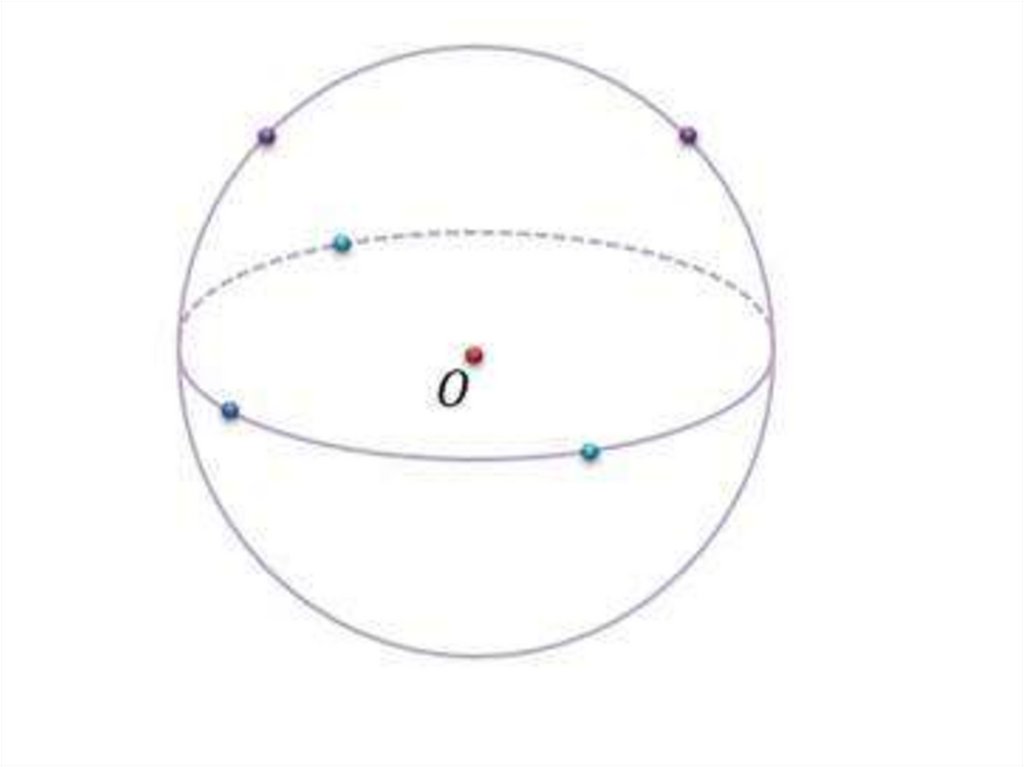
Сфера и шар
1. Сфера и шар.
2.
3. Сфера и шар.
4.
5.
6.
7.
8.
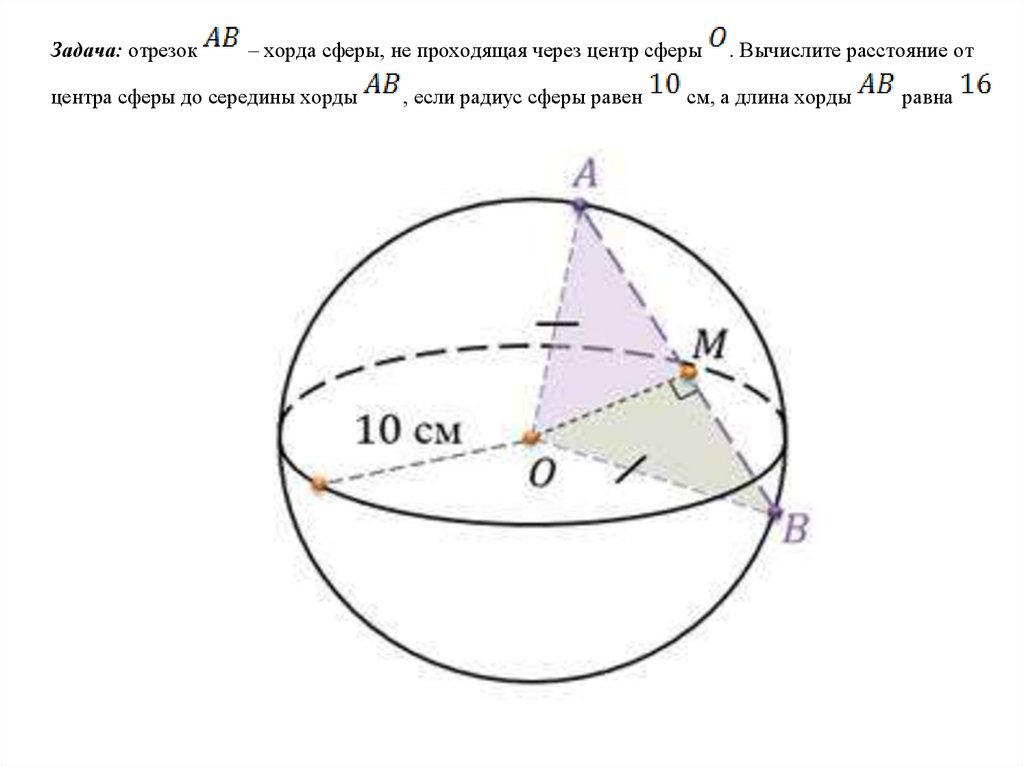
Задача: отрезок– хорда сферы, не проходящая через центр сферы
центра сферы до середины хорды
, если радиус сферы равен
. Вычислите расстояние от
см, а длина хорды
равна
9.
Решение: обозначим середину хордыРассмотрим
точкой
. Он равнобедренный, т.е.
.
, так как
. А как мы знаем,
все радиусы одной сферы равны между собой. Отсюда,
Теперь рассмотрим
. Он прямоугольный, так как отрезок
перпендикуляром проведённым к хорде
. Его катет
Воспользовавшись теоремой Пифагора найдём катет
центра сферы до середины хорды
что
(см).
является серединным
(см).
, который как раз таки и есть расстояние от
. Получаем,
(см).




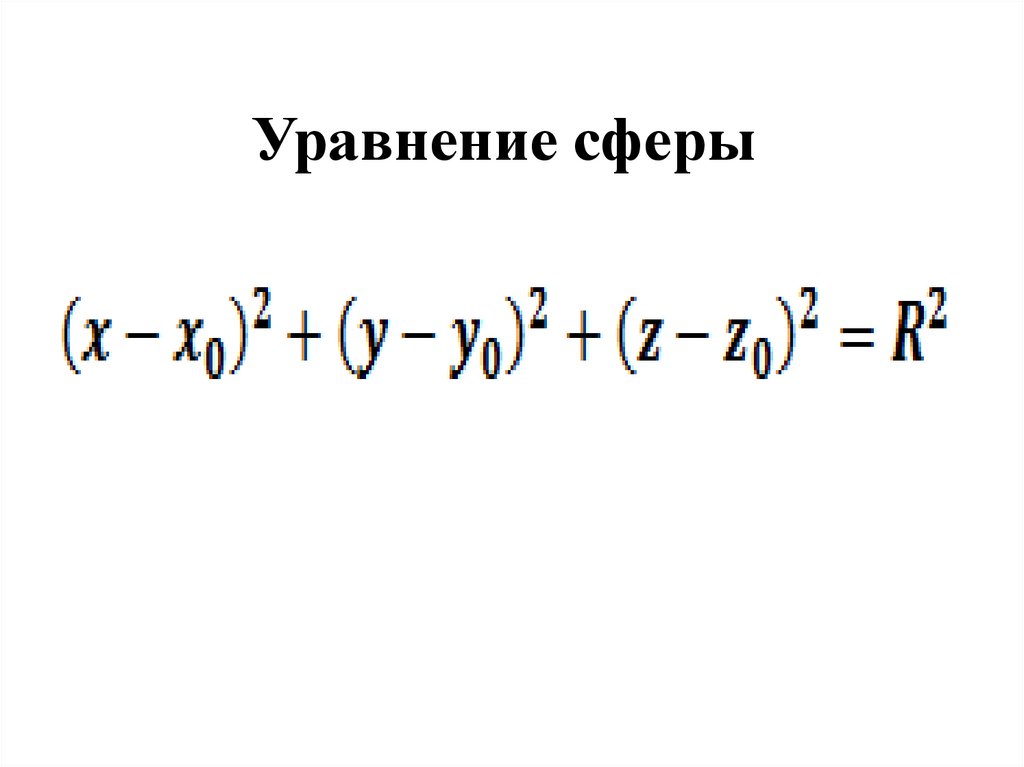
 Математика
Математика








