Уравнение и его корни. Уравнение с одной переменной. Задача

1. Уравнение и его корни

2. Уравнение с одной переменной

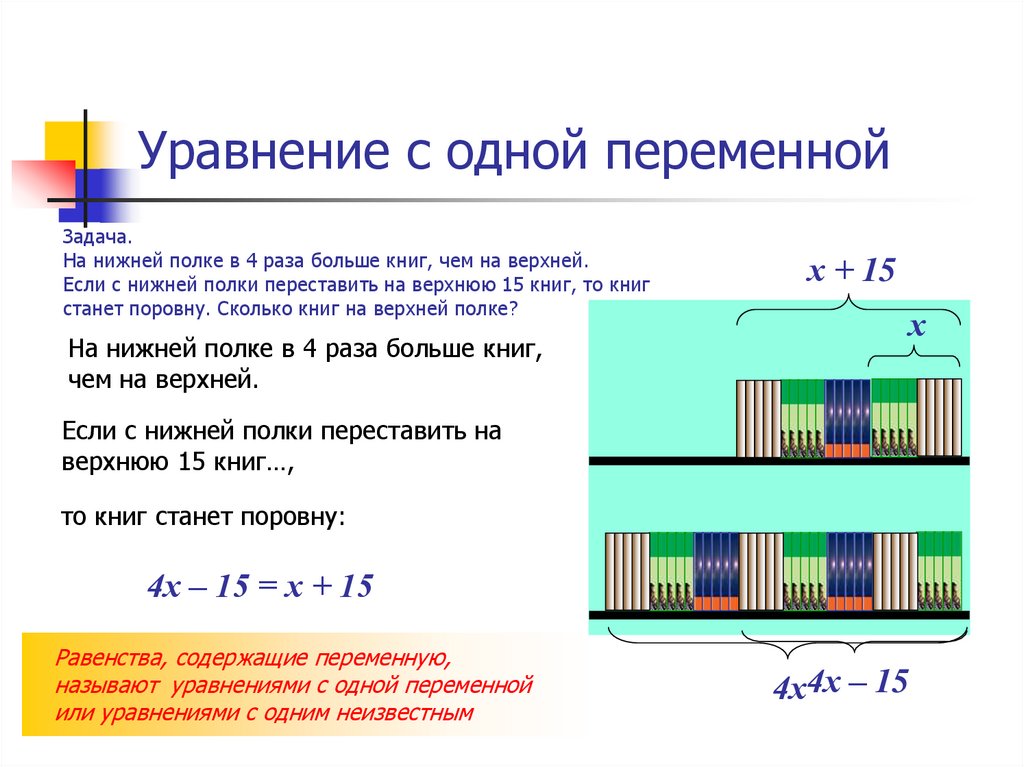
Задача.
На нижней полке в 4 раза больше книг, чем на верхней.
Если с нижней полки переставить на верхнюю 15 книг, то книг
станет поровну. Сколько книг на верхней полке?
На нижней полке в 4 раза больше книг,
чем на верхней.
х + 15
х
Если с нижней полки переставить на
верхнюю 15 книг…,
то книг станет поровну:
4х – 15 = х + 15
Равенства, содержащие переменную,
называют уравнениями с одной переменной
или уравнениями с одним неизвестным
4х4х – 15

3. Корень уравнения

Задача.
На нижней полке в 4 раза больше книг, чем на верхней.
Если с нижней полки переставить на верхнюю 15 книг, то книг
станет поровну. Сколько книг на верхней полке?
4х – 15 = х + 15
Корнем уравнения называется значение переменной,
при котором уравнение обращается в верное равенство
4 .10 – 15 = 10 + 15
х = 10 – корень уравнения

4. Решение уравнения

Задача.
На нижней полке в 4 раза больше книг, чем на верхней.
Если с нижней полки переставить на верхнюю 15 книг, то книг
станет поровну. Сколько книг на верхней полке?
4х – 15 = х + 15
4х – 15 = х + 15
– х + 15
Решить уравнение – значит найти все его корни
или доказать, что корней нет
Свойства уравнений:
Если в уравнении перенести слагаемое из одной
части в другую, изменив его знак, то получится
уравнение, равносильное данному.

5. Решение уравнения

Задача.
На нижней полке в 4 раза больше книг, чем на верхней.
Если с нижней полки переставить на верхнюю 15 книг, то книг
станет поровну. Сколько книг на верхней полке?
4х – 15 = х + 15
Решить уравнение – значит найти все его корни
или доказать, что корней нет
4х – х = 15 + 15
3 х = 30
:3
х = 10
Ответ: 10 книг.
Свойства уравнений:
Если в уравнении перенести слагаемое из одной
части в другую, изменив его знак, то получится
уравнение, равносильное данному.
Если обе части уравнения умножить или разделить
на одно и то же, отличное от нуля число, то
получится уравнение, равносильное данному.
Закрыть

English Русский Правила