Похожие презентации:
Решение систем линейных алгебраических уравнений по правилу Крамера, методом Гаусса
1. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ПО ПРАВИЛУ КРАМЕРА, МЕТОДОМ ГАУССА
Тема 1.2. Практика 5-6( 4 часа аудиторной работы)
2. Основные обозначения:
система линейных алгебраических уравнений(СЛАУ):
а11х1 а12 х2 ... а1n хn b1,
а х а х ... а х b ,
21 1 22 2
2n n
2
..............................................
аm1х1 аm 2 х2 ... аmn хn bm.
матричная запись СЛАУ:
где
а11
а
A 21
...
аm1
А Х=В ,
... а1n
... а2n
основная матрица системы,
... ...
... аmn
х1
b1
х
b
2
2
X столбец неизвестных системы, B столбец свободных членов
х
n
bm
а12
а22
...
аm 2
3.
4.
а11 а12расширенная
а
а22
21
матрица системы: A
...
...
аm1 аm 2
однородная
СЛАУ:
... а1n
... а2 n
... ...
... аmn
b1
b2
...
bm
а11х1 а12 х2 ... а1n хn 0,
а х а х ... а х 0,
21 1 22 2
2n n
..............................................
аm1х1 аm 2 х2 ... аmn хn 0 ;
;
5. Методы решения СЛАУ:
правило Крамера;матричный метод; (рассматриваться в
данной работе не будет)
метод Гаусса
6. Правило Крамера
Решает системы n – линейных алгебраическихуравнений с n – неизвестными общего вида
а11х1 а12 х2 ... а1n хn b1,
а х а х ... а х b ,
21 1 22 2
2n n
2
..............................................,
аn1х1 аn 2 х2 ... аnn хn bn,
причем определитель основной матрицы
системы отличен от нуля.
7.
Определение. Определитель, составленныйиз коэффициентов при неизвестных
системы называется главным
определителем системы, обозначается ∆:
а11 а12 ... а1i ... а1n
а21 а22 ... а2i ... а2 n
.
.... .... .... .... .... ....
аn1 аn 2 ... аni ... аnn
8. Правило Крамера
Вспомогательный определитель ∆i получается изопределителя ∆ путем замены соответствующего iго столбца столбцом свободных членов:
а11 а12 ... b1
а21 а22 ... b2
i
.... .... .... ....
аn1 аn 2 ... bn
... а1n
... а2 n
.... ....
... аnn
9. Теорема (правило Крамера)
Если главный определитель ∆ системы размерностиn n отличен от нуля, то система имеет решение, и
притом, единственное. Это решение можно найти
по формулам:
n
i
2
1
,
x1 , x2 , ... xi , ... , xn
10.
Рассмотрим системунеизвестными:
n
линейных
уравнений
c
n
a11x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
............................................
an1 x1 an 2 x2 ... ann xn bn
Теорема Крамера:
Пусть Δ - определитель матрицы системы,
Δi - определитель матрицы, получаемой из
матрицы A заменой
столбца коэффициентов
аij при xi столбцом свободных членов.
Тогда, если Δ ≠ 0, то система имеет единственное решение,
определяемое по формулам:
xj
j
- формула Крамера.
11.
Вспомним тему: ОпределителиОпределитель квадратной матрицы – это число,
вычисляемое по определённым правилам.
Обозначают: |А|, ΔА, detA .
Определитель 2-го
порядка:
a11 a12
2
a11 a22 a21a12
a21 a22
2 3
2 5 1 3 7
1 5
Боковая
диагональ
Главная
диагональ
12.
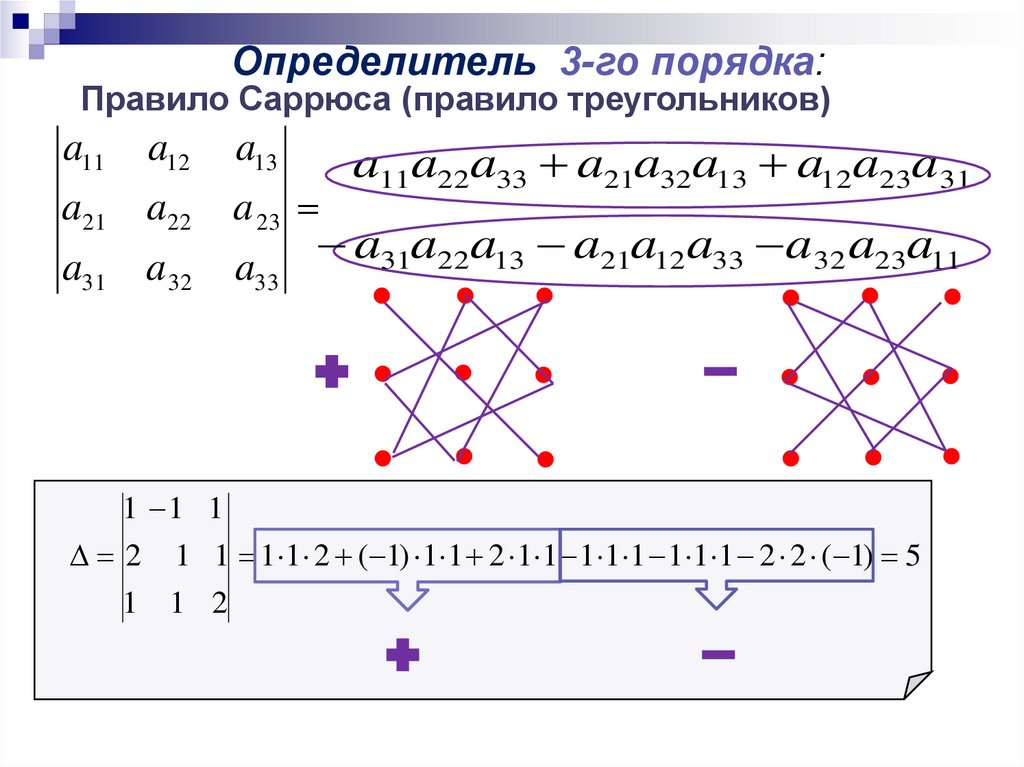
Определитель 3-го порядка:Правило Саррюса (правило треугольников)
a11 a12
a21 a22
a31 a 32
a13
a11a22a33 a21a32a13 a12a23a 31
a 23
a
a
a
a
a
a
a
a
a
31
22
13
21
12
33
32
23
11
a33
1 1 1
2 1 1 1 1 2 ( 1) 1 1 2 1 1 1 1 1 1 1 1 2 2 ( 1) 5
1 1 2
13.
Вспомним тему: Алгебраические дополнения иминоры
a11 a1 j ......a1n
ai1 aij ......ain
A
......................
a a .. .. a
nn
n1 nj
В квадратной матрице n-го
порядка рассмотрим элемент aij.
Вычеркнем i-ю строку и j-ый
столбец, на пересечении которых
стоит элемент aij. В результате
получается
матрица
(n-1)-го
порядка.
Минором Мij к элементу aij матрицы n-го порядка
называется определитель матрицы (n-1)-го порядка,
полученной из исходной матрицы вычеркиванием i-й
строки и
j-го столбца.
Алгебраическим дополнением Аij к элементу aij
матрицы n-го порядка называется его минор, взятый со
знаком «+», если сумма i+j четная, и со знаком «-»,
если сумма нечетная:
Aij 1 i. j M ij
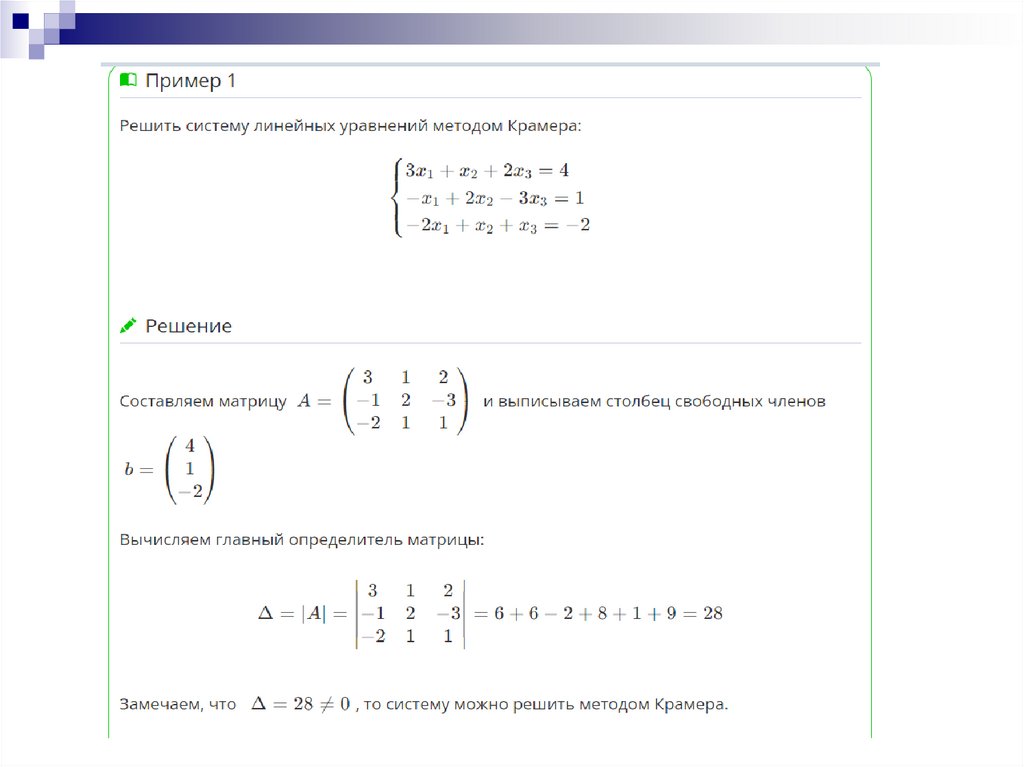
14. Рассмотрим сам алгоритм метода Крамера на конкретном примере
15.
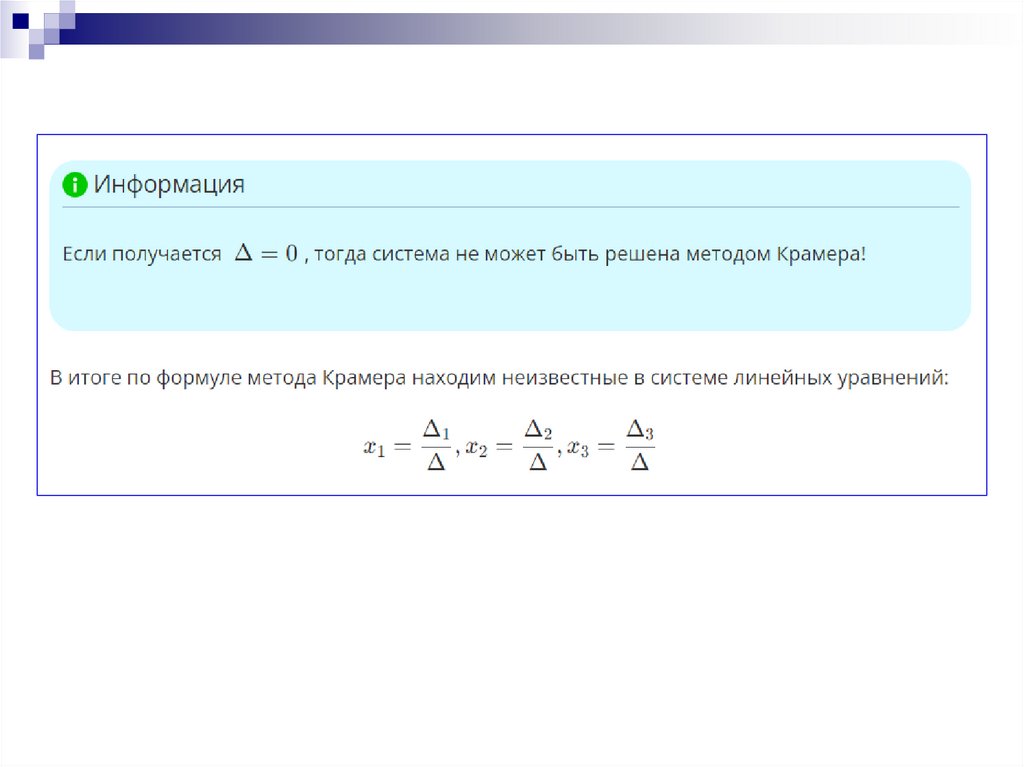
Если получается Δ=0, тогдасистема не может быть решена
методом Крамера!
16.
17.
18.
19.
20.
21.
Ответ: метод Крамера нельзя применить к данной системелинейных уравнений
22.
Пример. Решить систему методом Крамера:x1 2 x2 x3 0
2 x1 x2 3x3 0
x x x 1
3
1 2
1 2 1
Решение. 1)Определитель матрицы системы: 2 1 3 5 0
1
2) Вычислим определители
0 2 1
1 0 1 3 5
1 1
1
1
1
Δ1, Δ2, Δ3 :
1 0 1
2 2 0 3 5
1 1 1
1 2 0
3 2 1 0 5.
1 1 1
3) Подставим полученные значения в формулу Крамера:
1
5
x1
1,
5
2
5
x2
1,
5
3 5
x3
1
5
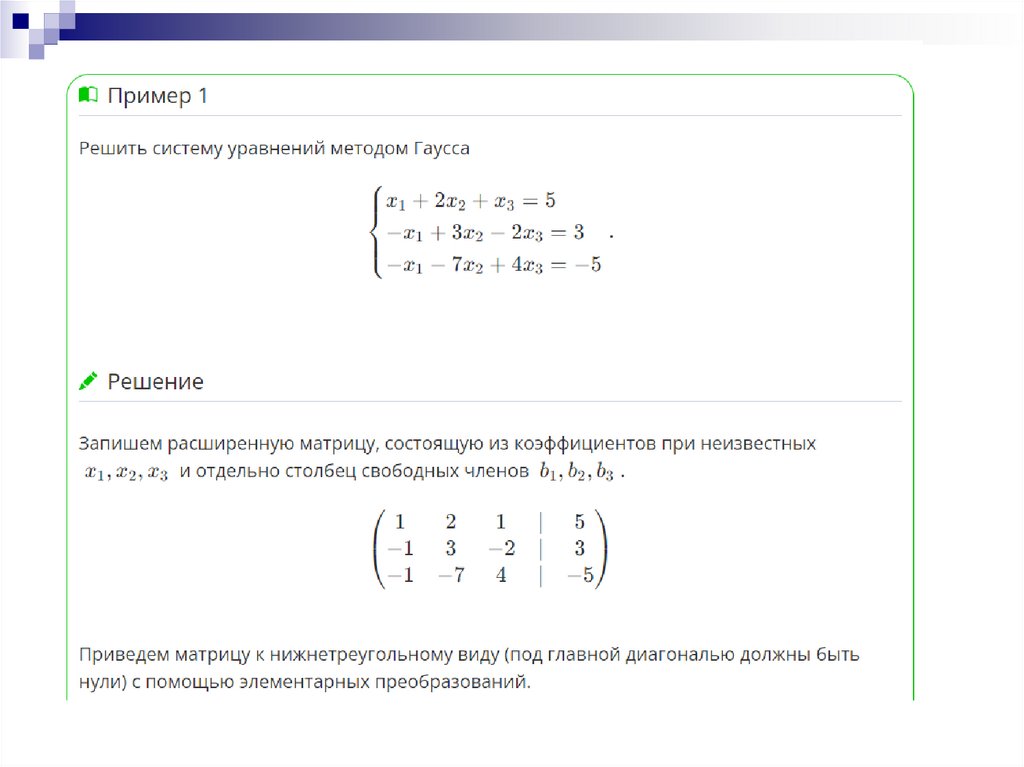
23. Метод Гаусса решения СЛАУ
24.
25. Метод Гаусса
Метод Гаусса — классический метод решения системылинейных алгебраических уравнений (СЛАУ).
Это метод последовательного
исключения переменных, когда с помощью
элементарных преобразований система уравнений
приводится к равносильной системе ступенчатого
(или треугольного) вида, из которого
последовательно, начиная с последних (по номеру)
переменных, находятся все остальные переменные.
26.
Суть метода ГауссаЧтобы решить систему m – линейных
алгебраических уравнений с n – неизвестными
методом Гаусса, необходимо записать
расширенную матрицу системы и, используя
элементарные преобразования расширенной
матрицы системы, привести ее к трапециевидной
форме.
27.
Элементарные преобразования расширеннойматрицы системы :
1. перестановка строк (столбцов) матрицы;
2. умножение строки матрицы на действительное
число отличное от нуля и сложение с другой
строкой;
3. вычеркивание строки матрицы, все элементы
которой равны нулю;
4. вычеркивание одной из пропорциональных строк
матрицы;
5. умножение строки матрицы на число отличное от
нуля.
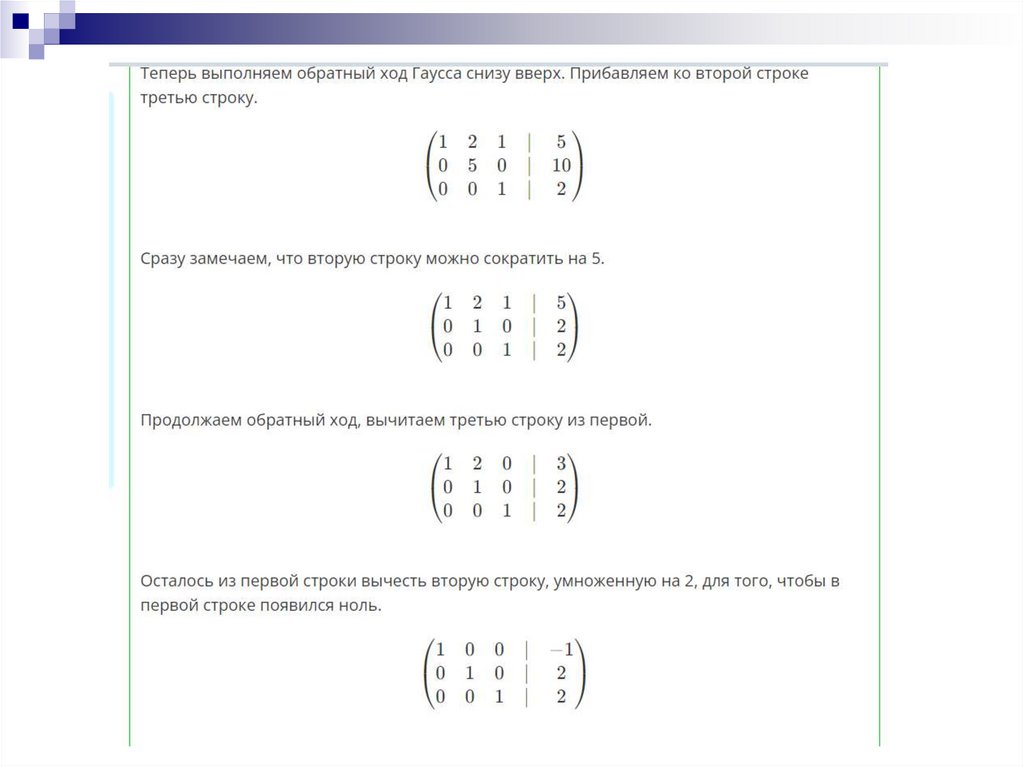
28. Рассмотри пример решения СЛАУ методом Гаусса
29.
30.
31.
32.
33.
234.
35.
36.
Не забудь прикрепитьфото выполненной работы
в СДО Moodle
Спасибо за внимание!!! =)































 Математика
Математика








