Логические функции. Построение таблиц истинности логических функций. Тождественная истинность

1.

Логические функции.
Построение таблиц истинности
логических функций.
Тождественная истинность.

2.

Приоритет логических операций
1.
2.
3.
4.
5.
6.
Операции в скобках.
Отрицание.
Логическое умножение.
Логическое сложение.
Импликация.
Эквивалентность.
Определите, в каком порядке необходимо вычислять
значение логического выражения:
3
1
1) ¬ А & ¬2 B
2
1
2) A & (B & C)
3
4
2 1
3) (A & B) ν (C & ¬ D)
2 1
3
4) A ν ¬ D ν B
3
2
1
5) A → (B ↔ ¬ A)

3.

Вычисление значений логических выражений
Пример1.
Вычислить значение логического выражения
F=«(2·2=5 или 2·2=4) и (2·2 ≠ 5 или 2·2 ≠ 4)»
Обозначим
А=«2·2=5» – ложно (0)
В=«2·2=4» – истинно (1)
Тогда F=(А или В) и (А или В )
F (A B) (A B) (0 1) (1 0) 1 1 1

4.

Вычисление значений логических выражений
Пример 2. Определите истинность составного высказывания
( A & B) & (C D) состоящего из простых высказываний:
А={Принтер – устройство вывода информации}
В={Процессор – устройство хранения информации}
C={Монитор – устройство вывода информации}
D={Клавиатура – устройство обработки информации}
Установим истинность простых высказываний:
А=1, В=0, С=1, D=0
Определяем истинность составного высказывания:
F= ( А& В) &( C v D) =
(1 & 0) & (1 0) (0 & 1) & (1 0) 0 & 1 0

5.

Вычисление значений логических выражений
Пример 3. Найти значения логического выражения:
1) (1 1) (1 0) 1 1 1
2) (0 & 1) & 1 0 &1 0
3) ((1 0) & (1 & 1)) & (0 1) (1 & 1) & 1 1 & 1 1
4) (0V1)→(1&1)= 1→1= 1
5) (1&1V0)↔( 1&1)= 1↔0 = 0
6) ((1→0)↔(1&1)V1)= (0↔1)= 0= 1

6.

Логические функции
Логической (булевой) функцией называют функцию
F(Х1, Х2, ..., Хn), аргументы которой Х1, Х2, ..., Хn
(независимые переменные) и
сама функция (зависимая переменная) принимают
значения 0 или 1.

7.

Таблица истинности
Таблицу, показывающую, какие значения принимает
логическая функция при всех сочетаниях значений ее
аргументов, называют таблицей истинности логической
функции.
Таблица истинности логической функции n аргументов
содержит 2n строк, n столбцов значений аргументов и 1
столбец значений функции.
Логические функции могут быть заданы табличным
способом или аналитически — в виде соответствующих
формул.
Каждая логическая функция двух переменных имеет 4
возможных набора значений, то существует 16 различных
логических функций от двух переменных: N=24=16.

8.

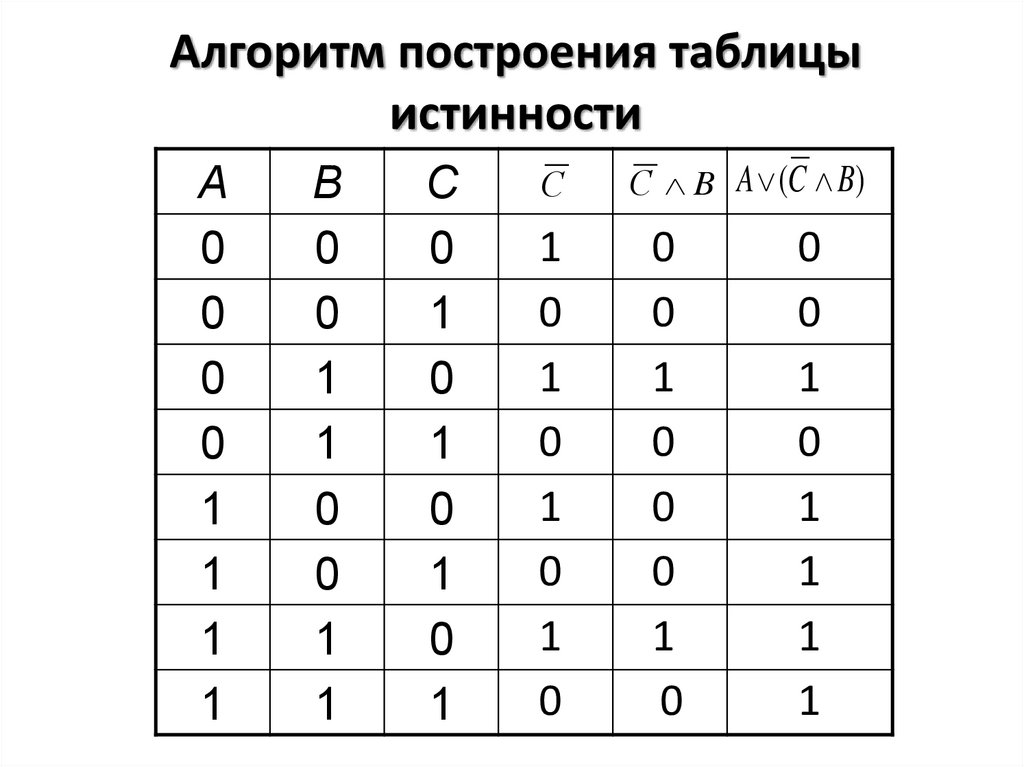
Алгоритм построения таблицы
истинности
1. Определить количество строк в таблице по формуле 2n +
1, где n – количество входящих в выражение логических
переменных;
2. Определить количество столбцов в таблице как сумму
количества логических переменных и операций или
промежуточных формул.
3. Определить порядок выполнения операций в исходной
формуле с учетом приоритетов и скобок.
4. Найти значения промежуточных формул и конечного
результата в соответствии с таблицами истинности.
Построить таблицу истинности для следующей функции:
F ( A, B, C ) A (C B)

9.

Алгоритм построения таблицы
истинности
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
С
1
0
1
0
1
0
1
0
С B A (C B)
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
1

10.

Построить таблицы истинности для
следующих функций

11.

Тождественно истинные, тождественно
ложные, эквивалентные сложные
высказывания (формулы)
• Если сложное высказывание истинно при всех
значениях входящих в него переменных, то такое
высказывание называется тождественно истинным
или тавтологией (обозначается константой 1).
• Если сложное высказывание ложно при всех значениях
входящих в него переменных, то такое высказывание
называется тождественно ложным (обозначается
константой 0).
• Если значения сложных высказываний совпадают на
всех возможных наборах значений входящих в них
переменных, то такие высказывания называют
равносильными, тождественными,
эквивалентными.

12.

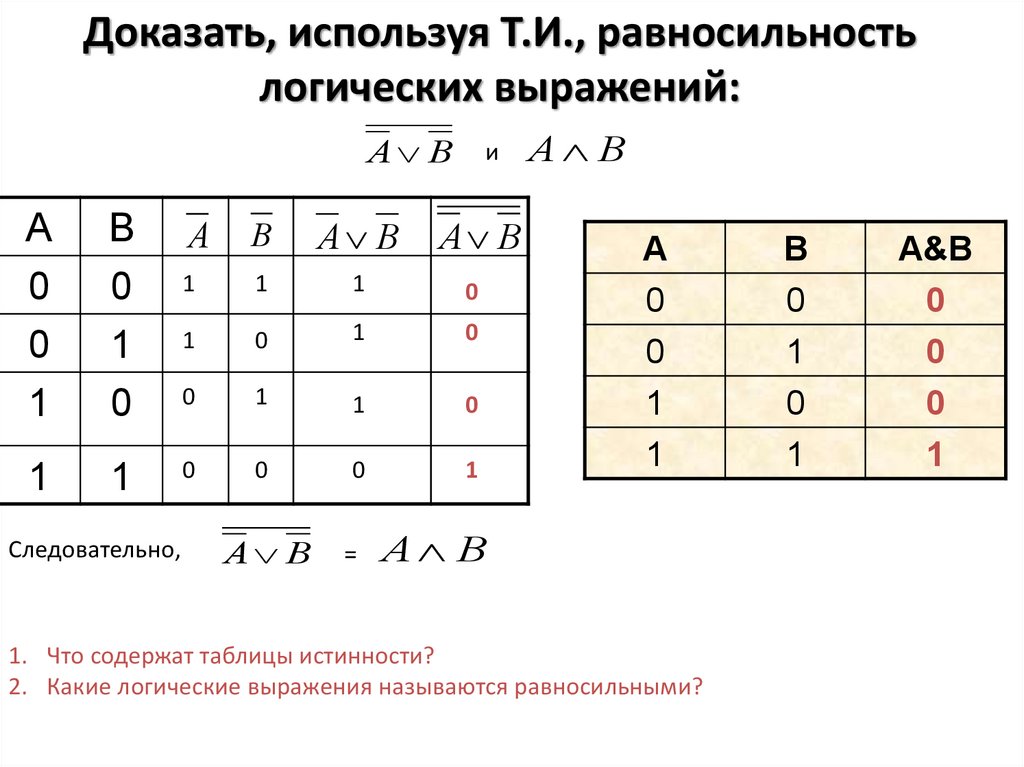
Доказать, используя Т.И., равносильность
логических выражений:
А В
А
0
0
1
В
0
1
0
1
1
Следовательно,
и
А
В
А В
1
1
1
0
1
0
1
0
0
1
1
0
0
0
0
1
А В
=
А В
А В
А
0
0
В
0
1
А&B
0
0
1
1
0
1
0
1
А В
1. Что содержат таблицы истинности?
2. Какие логические выражения называются равносильными?