Похожие презентации:
Преобразование графиков тригонометрических функций. Интегрированный урок (математика-информатика)
1. Интегрированный урок (математика-информатика)
Преобразованиеграфиков
тригонометрических
функций
2. Цели:
Освоить общие приемы построенияПовторить технику построения графика
квадратичной функции для различных
ситуаций
Научить применять изученные приемы
построения графиков в измененной
ситуации
3. Образовательные задачи:
Актуализация знаний о графиках функцийЗакрепление знаний о построении
графиков квадратичной функции
Перенос знаний в новые условия
4. Развивающие задачи:
Развитие логического мышления,познавательного интереса, творческой
активности
Развитие общеучебных навыков и умений
– организационных, интеллектуальных и
коммуникативных
5. Воспитательные задачи:
Воспитание взаимопомощи, культурыобщения, способствующей созданию
благоприятного психологического климата,
направленного на личностноориентированный подход к обучению и
воспитанию
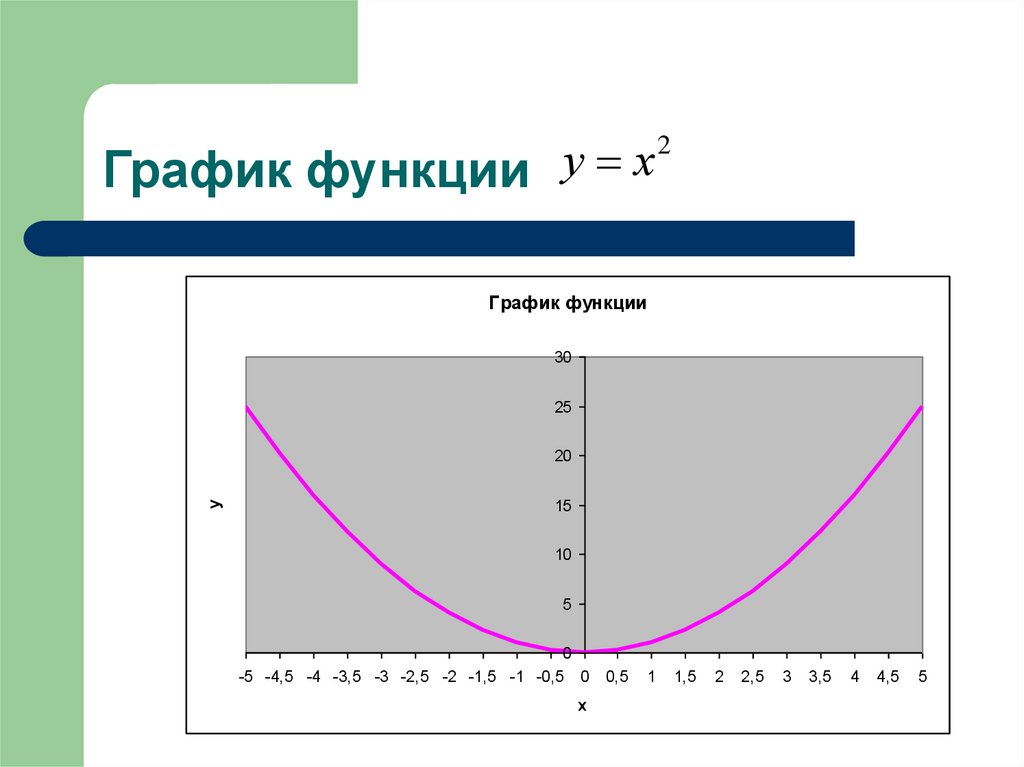
6. График функции
2у
х
График функции
График функции
30
25
у
20
15
10
5
0
-5 -4,5 -4 -3,5 -3 -2,5 -2 -1,5 -1 -0,5 0 0,5
х
1
1,5
2
2,5
3
3,5
4
4,5
5
7. График функции
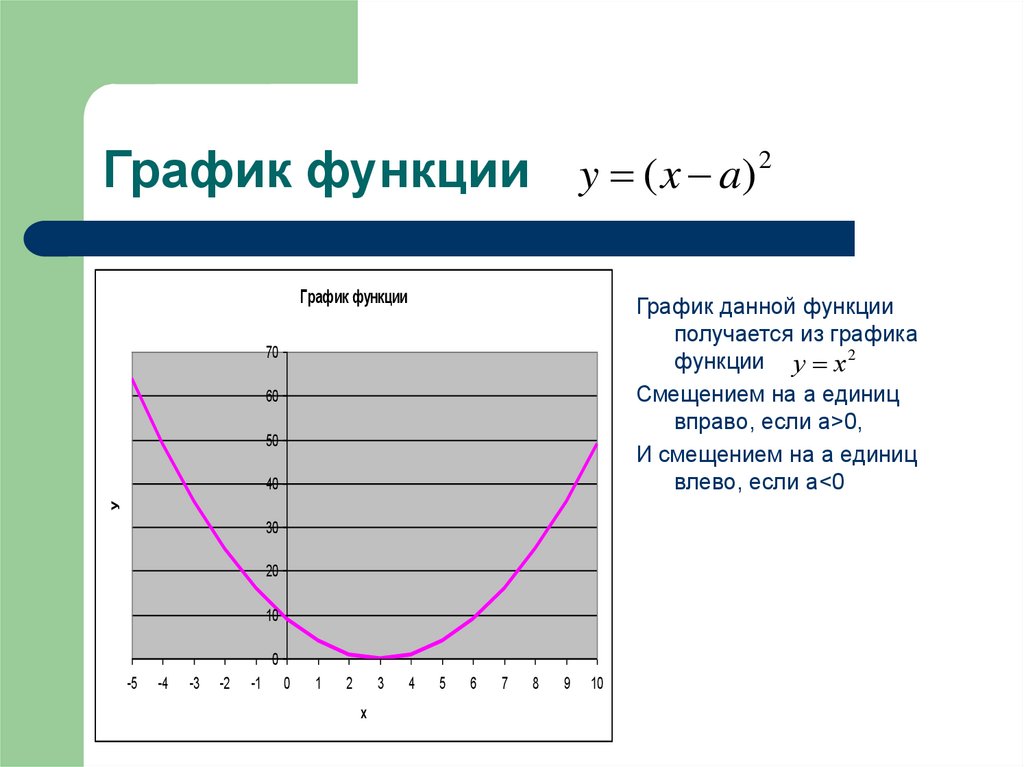
y ( x a)График функции
График данной функции
получается из графика
функции у х 2
Смещением на а единиц
вправо, если а>0,
И смещением на а единиц
влево, если а<0
70
60
50
у
40
30
20
10
0
-5
-4
-3
-2
-1
0
1
2
3
х
2
4
5
6
7
8
9
10
8. График функции
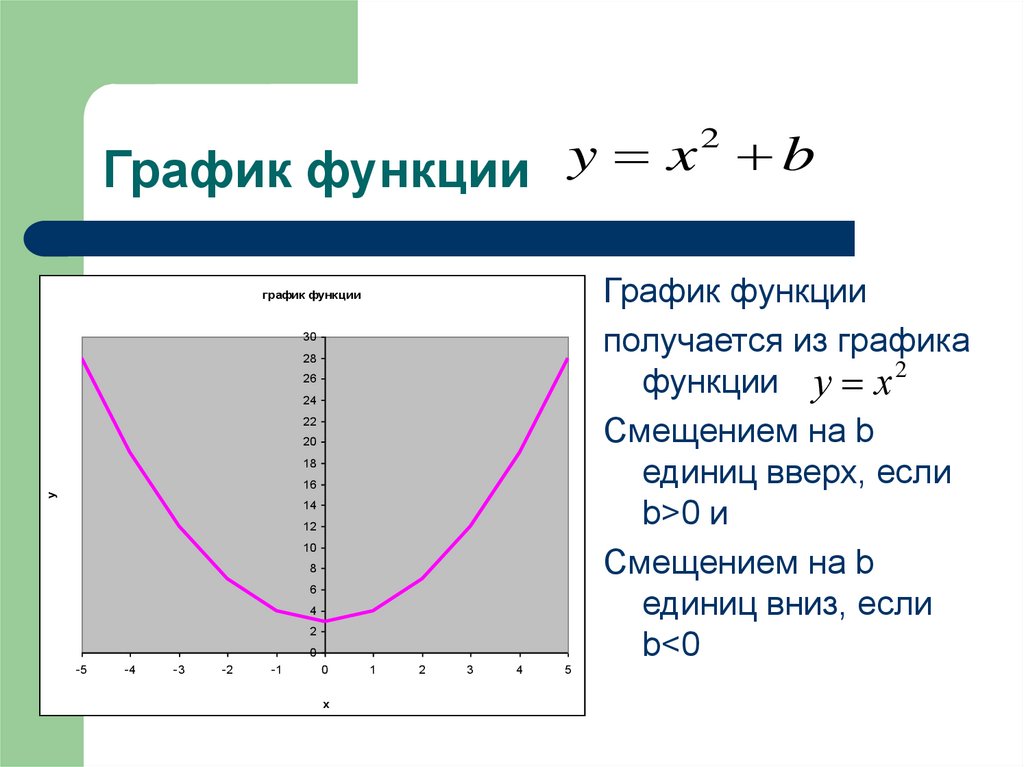
y x b2
График функции
получается из графика
функции у х 2
Смещением на b
единиц вверх, если
b>0 и
Смещением на b
единиц вниз, если
b<0
график функции
30
28
26
24
22
20
18
у
16
14
12
10
8
6
4
2
0
-5
-4
-3
-2
-1
0
х
1
2
3
4
5
9. График функции
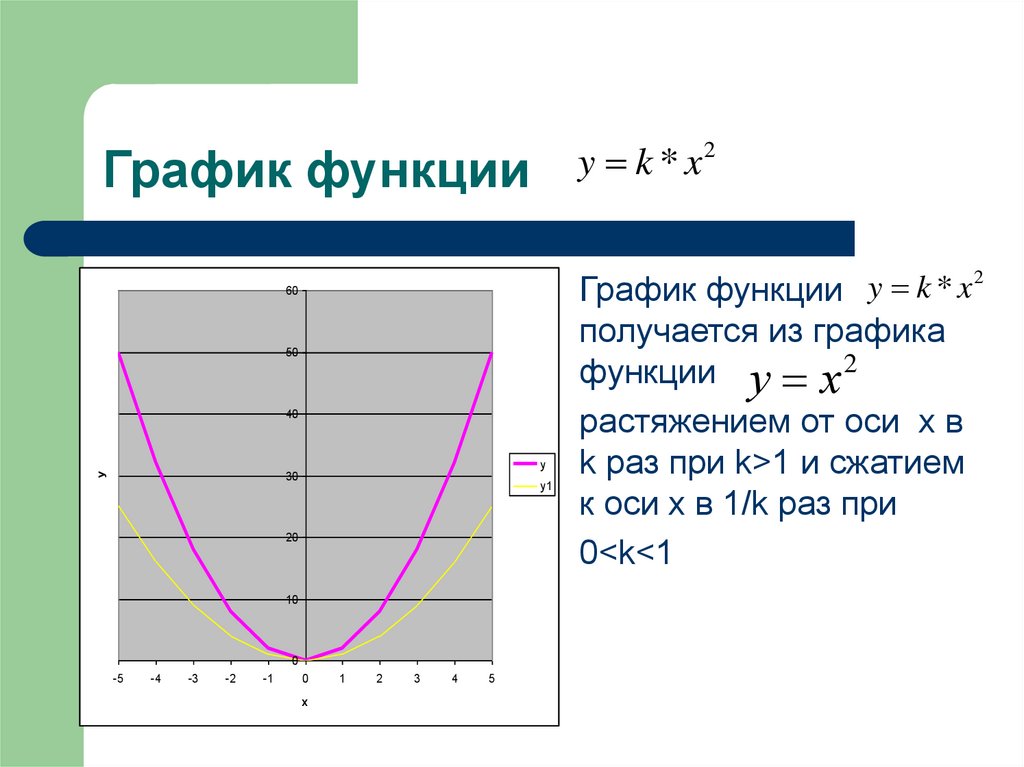
y k * x2График функции
2
y
k
*
x
График функции
60
50
40
у
у
30
у1
20
10
0
-5
-4
-3
-2
-1
0
х
1
2
3
4
5
получается из графика
функции у х 2
растяжением от оси х в
k раз при k>1 и сжатием
к оси х в 1/k раз при
0<k<1
10. График функции
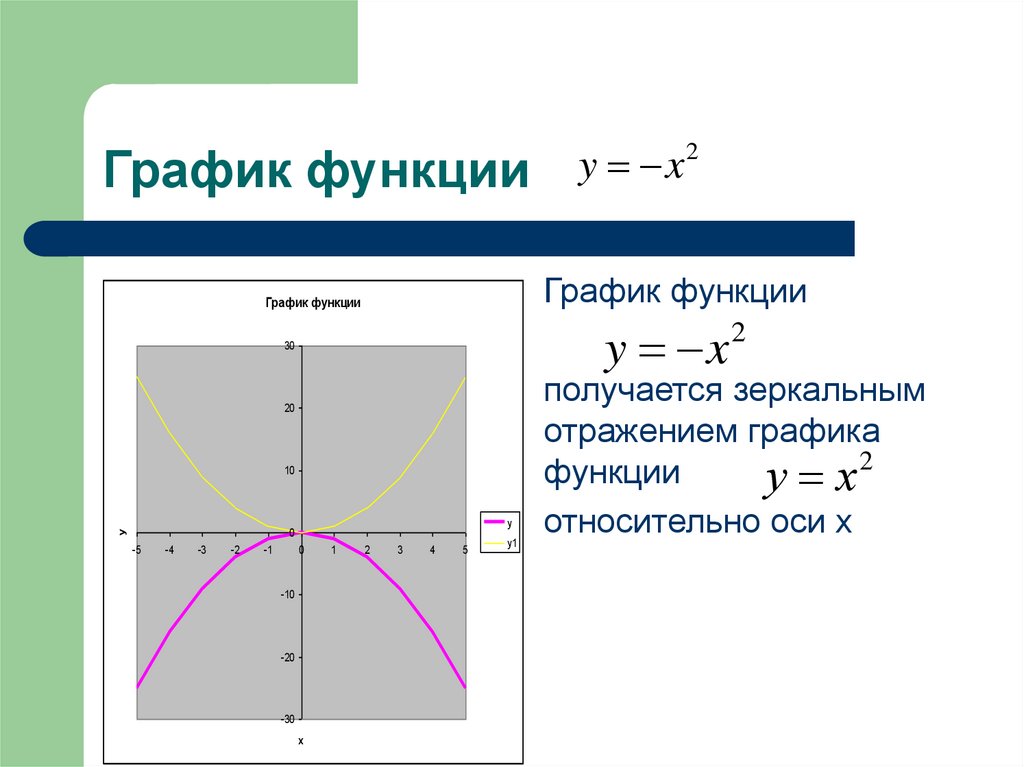
График функцииГрафик функции
y x2
30
20
10
у
у
0
-5
-4
-3
-2
-1
y x2
0
-10
-20
-30
х
1
2
3
4
5
у1
получается зеркальным
отражением графика
2
функции
у х
относительно оси х
11. График функции
yx
2
*
x
3
График функции
2
График функции
35
30
25
20
15
у
у
10
5
0
-5
-4
-3
-2
-1
0
-5
-10
х
1
2
3
4
5
12. График функции
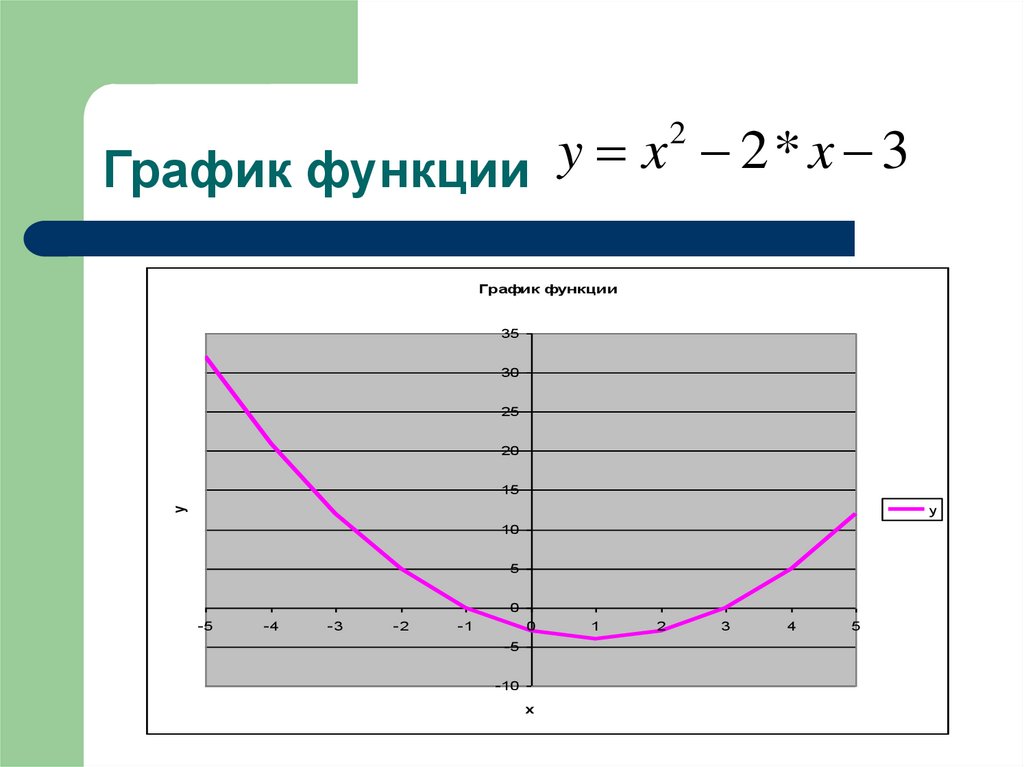
y x2 2 * x 3График функции
35
30
25
20
у
у
15
10
5
0
-5
-4
-3
-2
-1
0
х
1
2
3
4
5
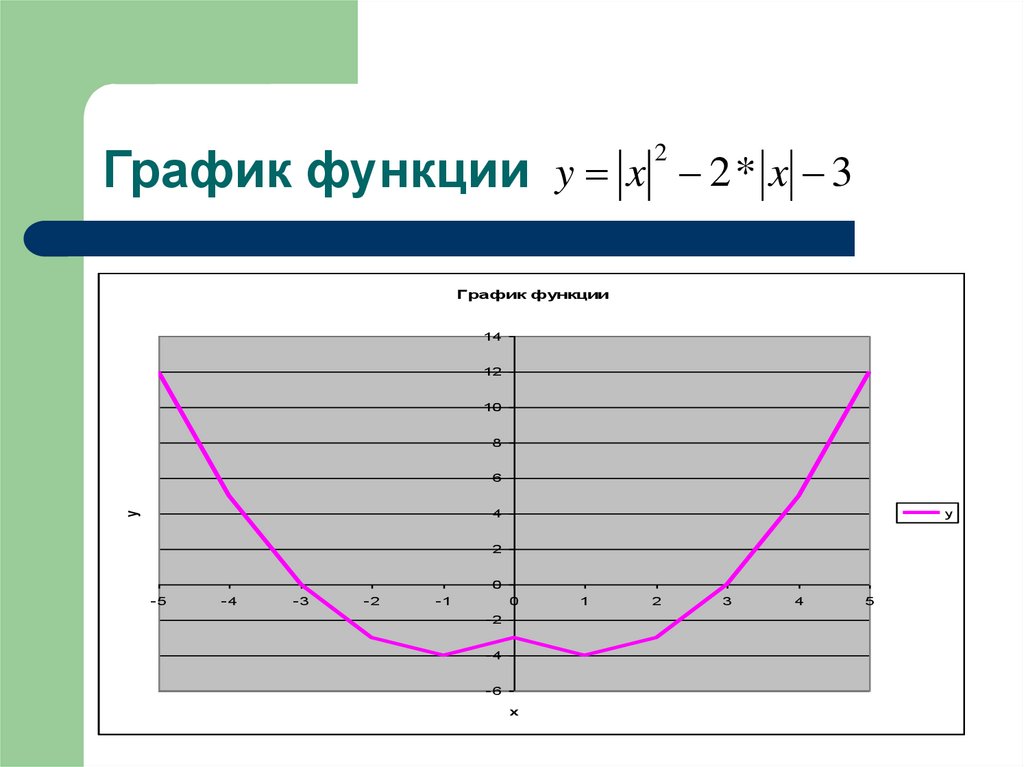
13. График функции
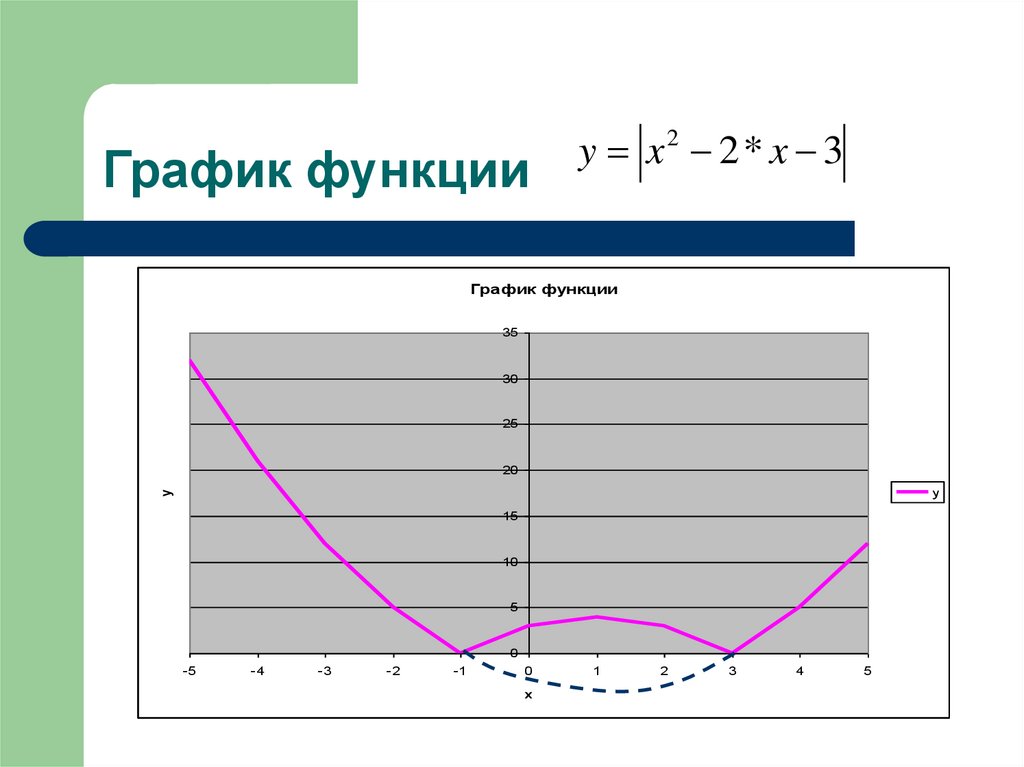
y x 2 * x 32
График функции
14
12
10
8
6
у
4
у
2
0
-5
-4
-3
-2
-1
0
-2
-4
-6
х
1
2
3
4
5
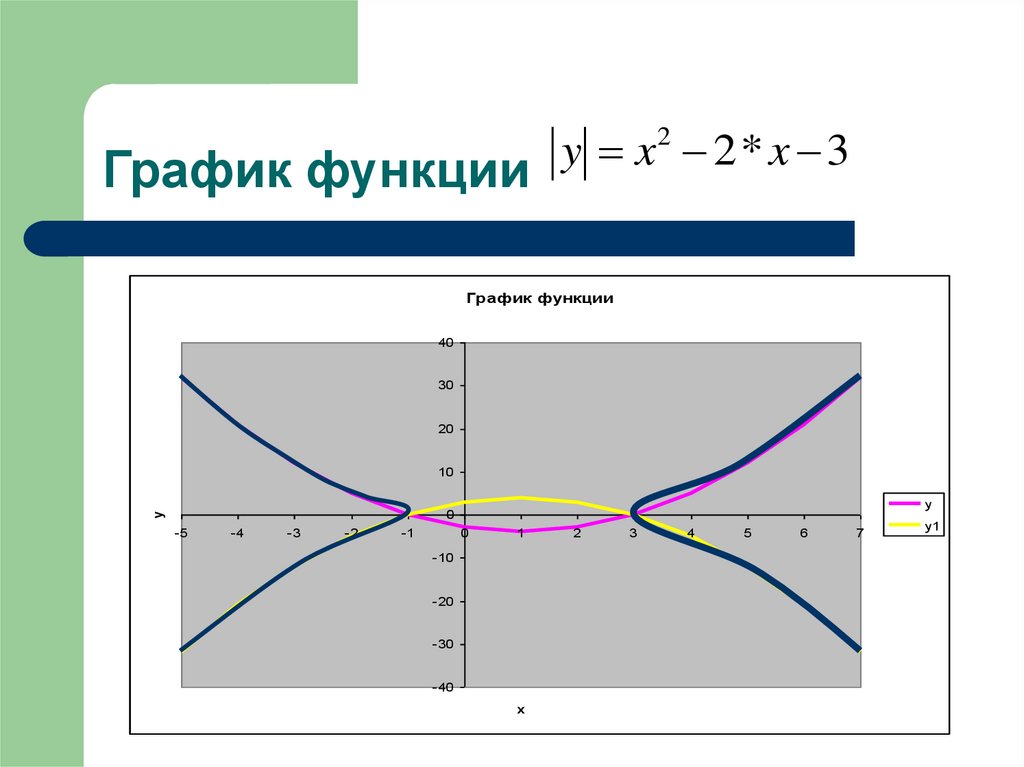
14. График функции
y x 2* x 32
График функции
40
30
20
10
у
у
0
-5
-4
-3
-2
-1
0
1
-10
-20
-30
-40
х
2
3
4
5
6
7
у1
15. Выводы:
Параллельный перенос (сдвиг):график функции y f ( x a) получается из графика
функции y=f(x) смещением на а единиц вправо,
если а>0,и смещением на а единиц влево, если
а<0
График функции y=f(x)+b получается из графика
функции y=f(x) смещением на b единиц вверх,
если b>0 и смещением на b единиц вниз, если b<0
16.
Деформация (растяжение и сжатие) графикаГрафик функции y=f(kx), k>0 получается из
графика функции y=f(x) «сжатием» к оси y
в k раз при k>1 и «растяжением» от оси y
в 1/k раз при 0<k<1.
График функции y=kf(x), k>0 получается из
графика функции y=f(x) «растяжением» от
оси х в k раз при k>1 и «сжатием» к оси x в
1/k раз при 0<k<1
17.
Отражение:График функции y=-f(x) получается
зеркальным отражением графика функции
y=f(x) относительно оси х
График функции y=f(-x) получается
зеркальным отражением графика функции
y=f(x) относительно оси y
18.
Графиков, содержащих модули:График функции у f (x) получается из графика функции y=f(x)
зеркальным отображением части графика, лежащей ниже
оси Ох
График функции y f ( x ) получается зеркальным
отображением части графика, лежащего справа от оси Оy
относительно оси Оy
График функции y f (x) получается из части графика
функции y=f(x), лежащей выше оси Ох и ее зеркальным
отображением относительно оси Ох
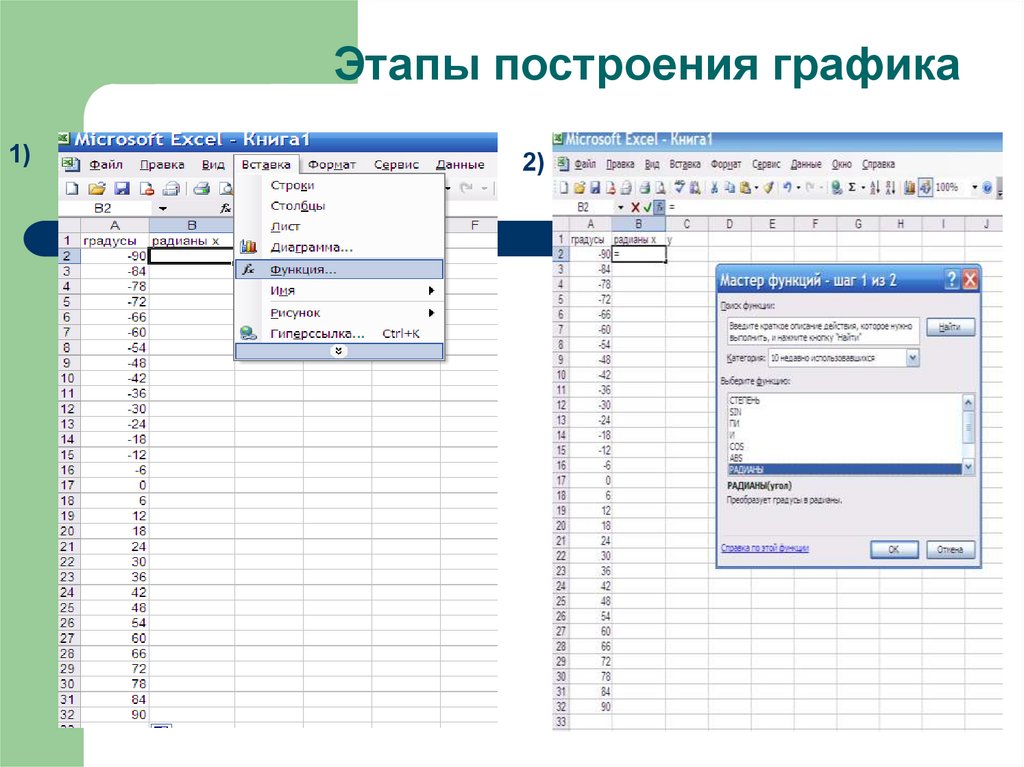
19. Этапы построения графика
1)2)
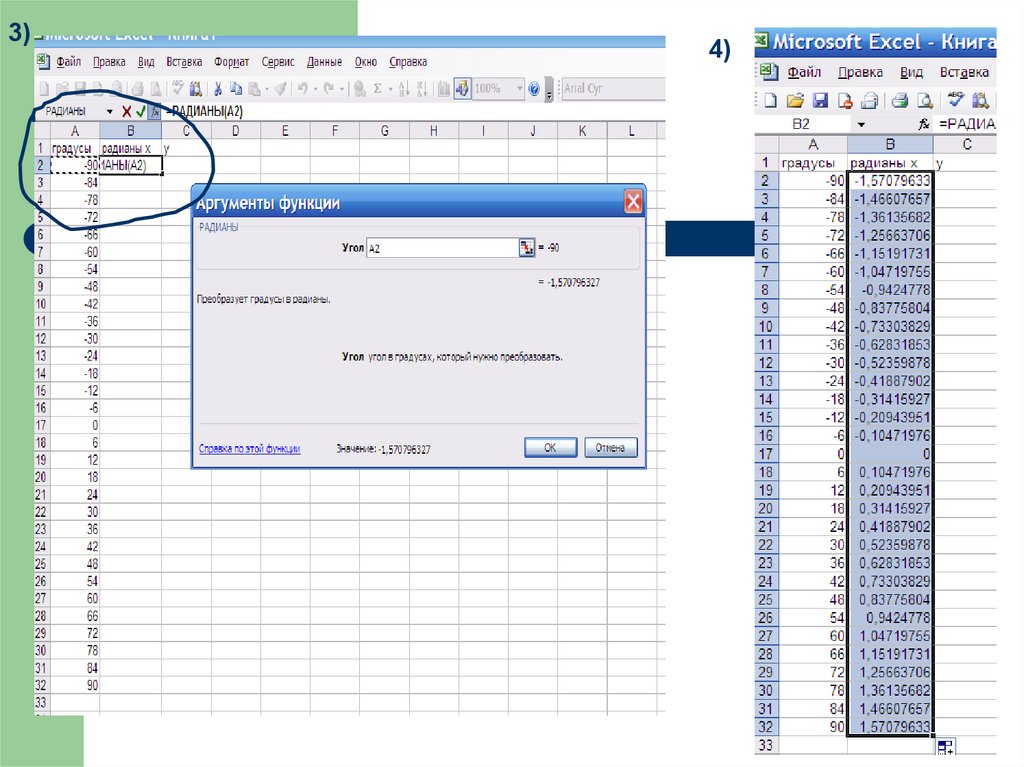
20.
3)4)
21.
5)6)
22.
7)8)
23.
9)10)
24.
11)12)
25.
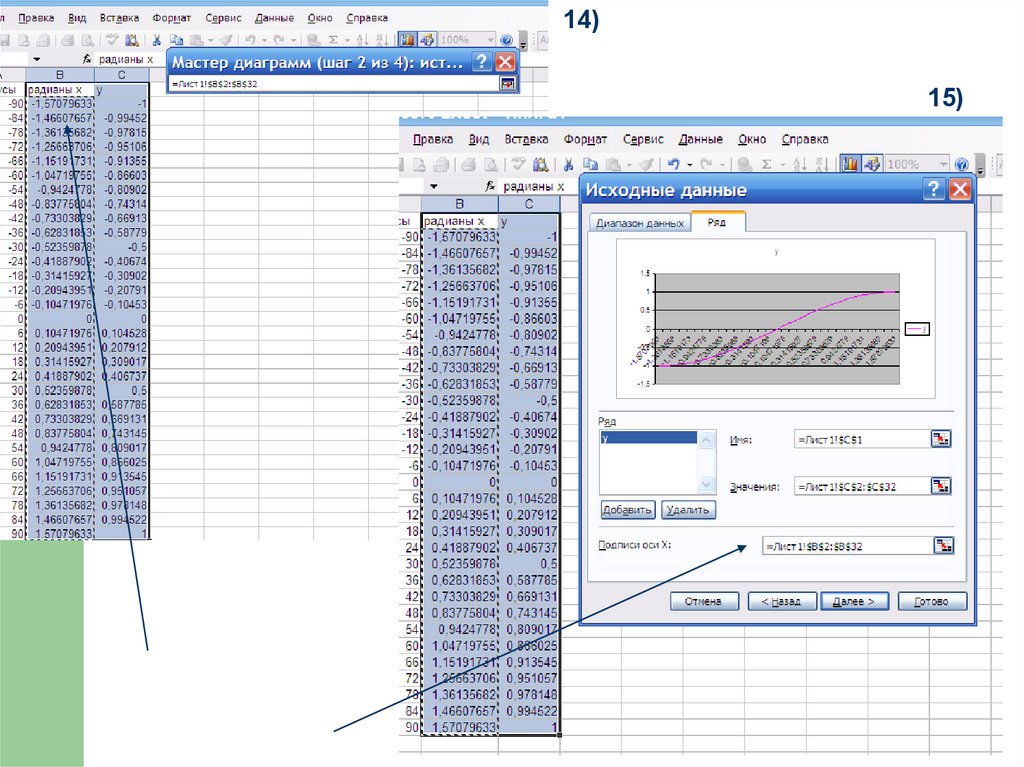
14)15)
26.
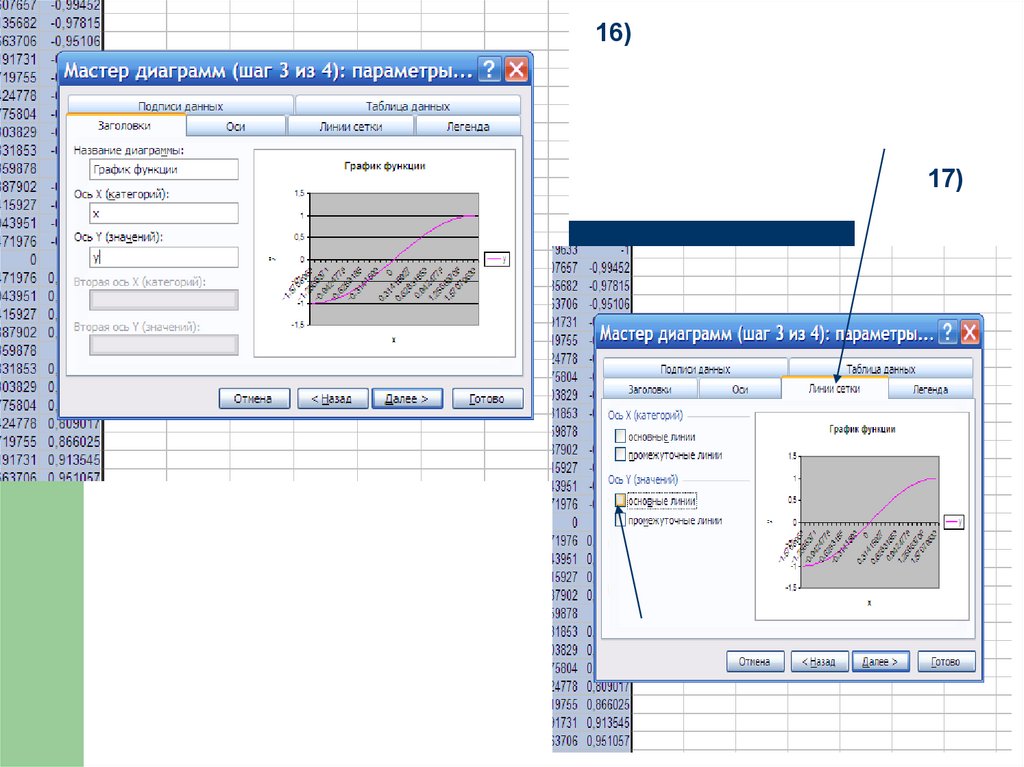
16)17)
27.
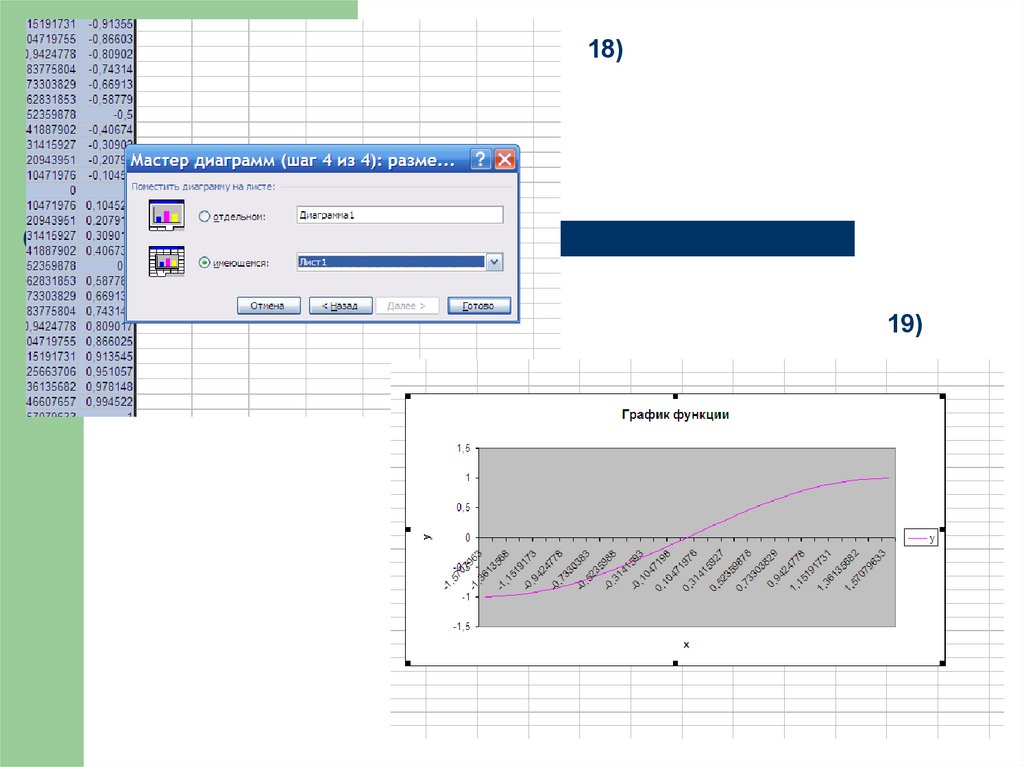
18)19)
28.
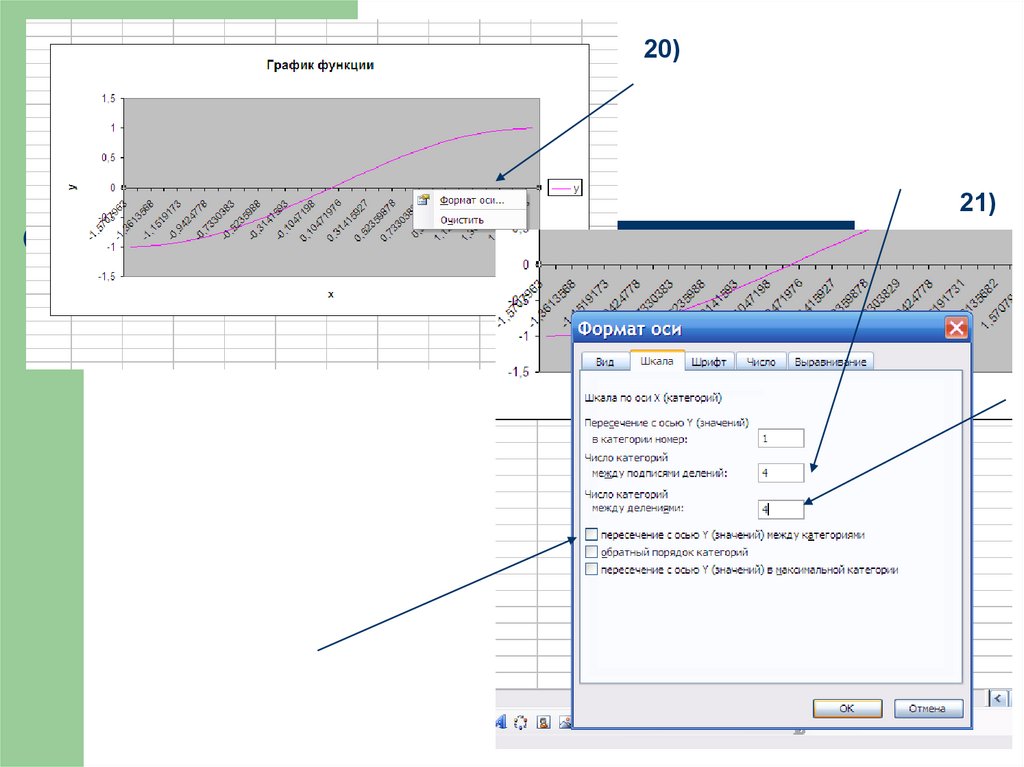
20)21)
29.
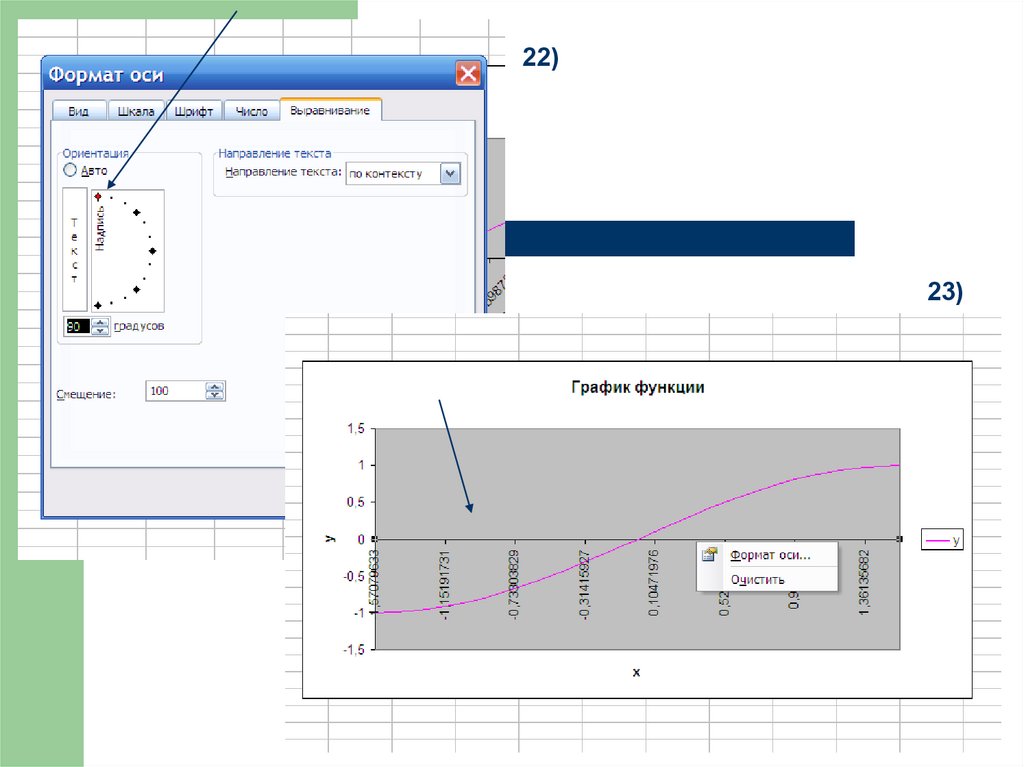
22)23)
30.
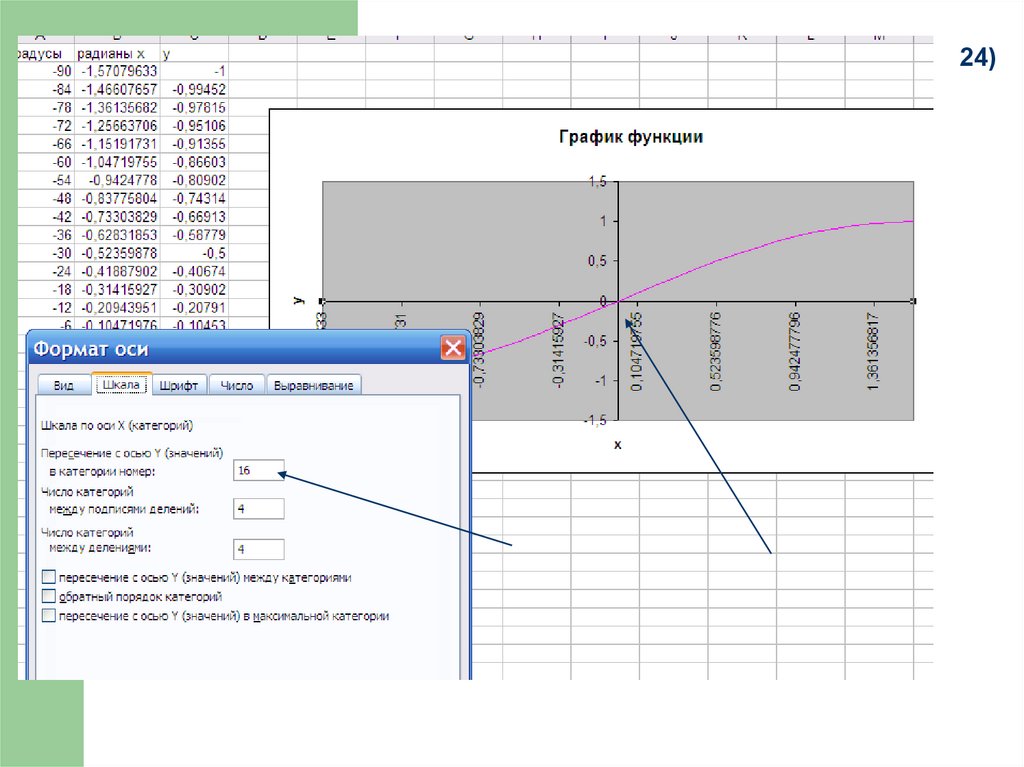
24)31.
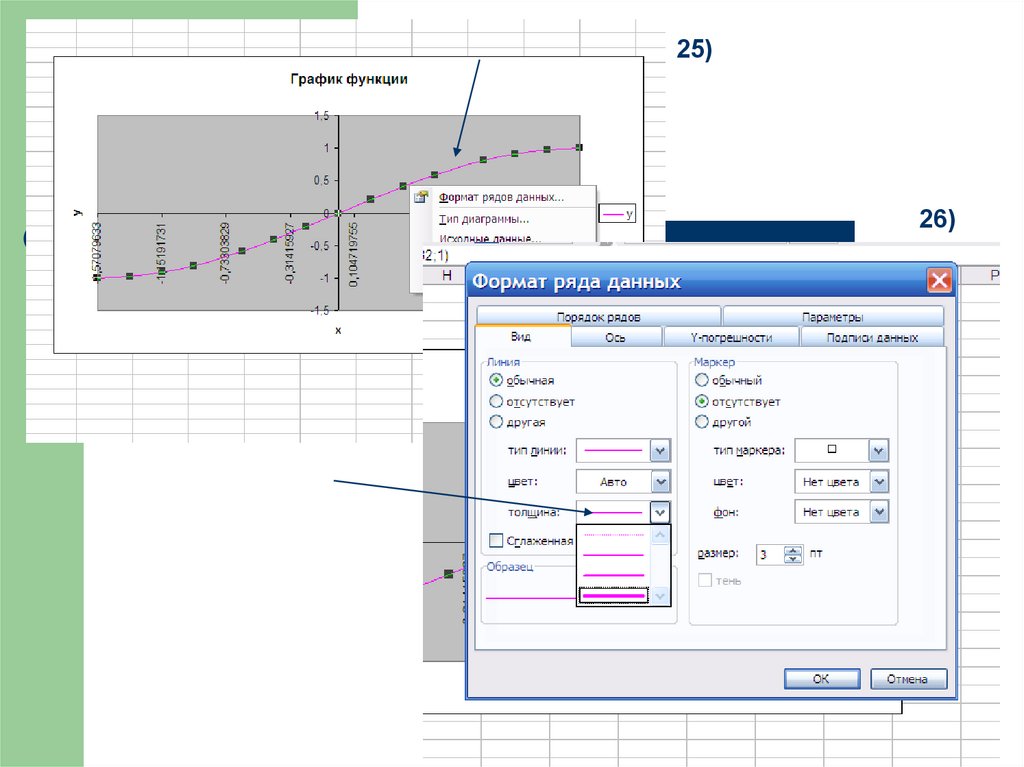
25)26)
32.
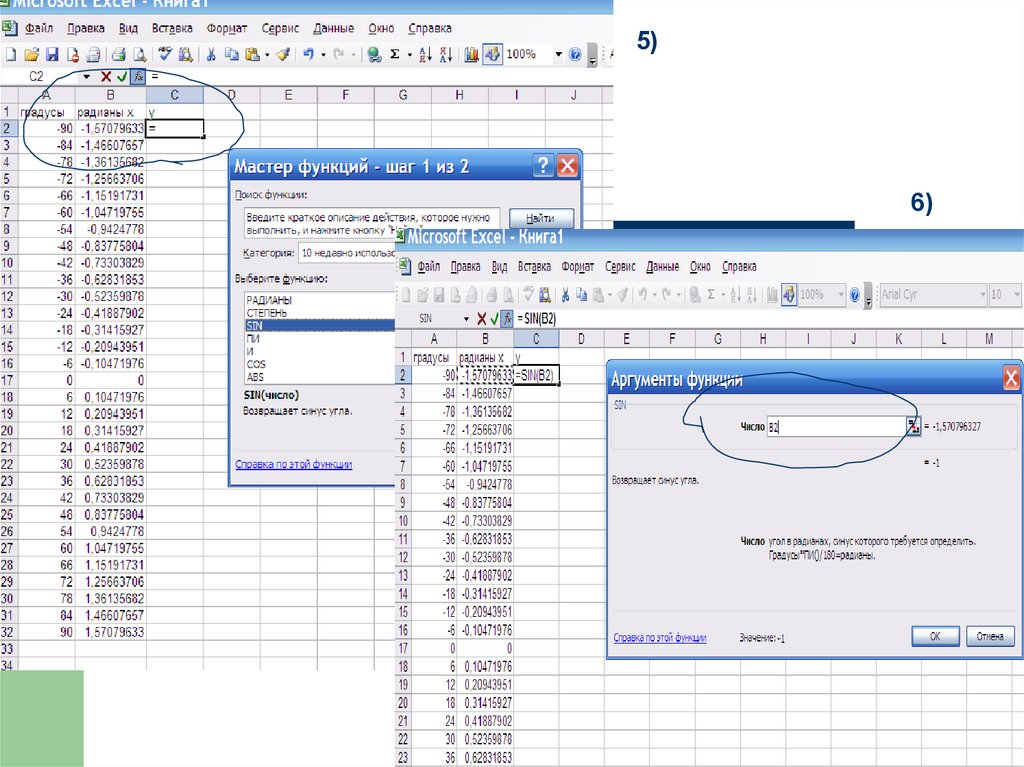
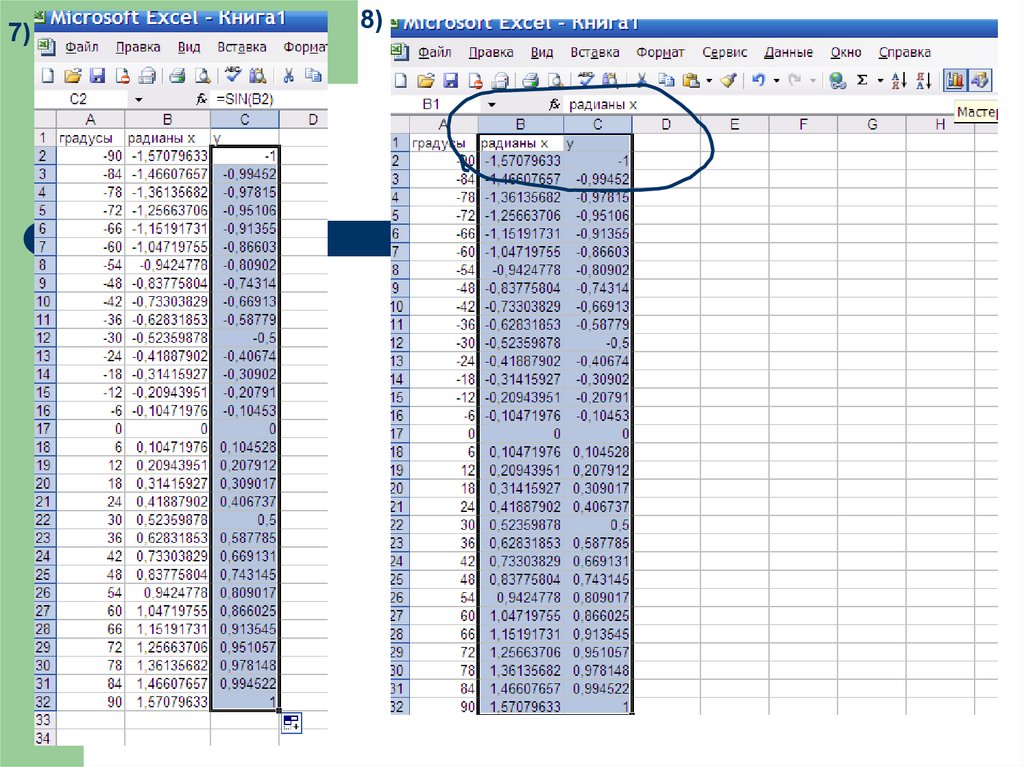
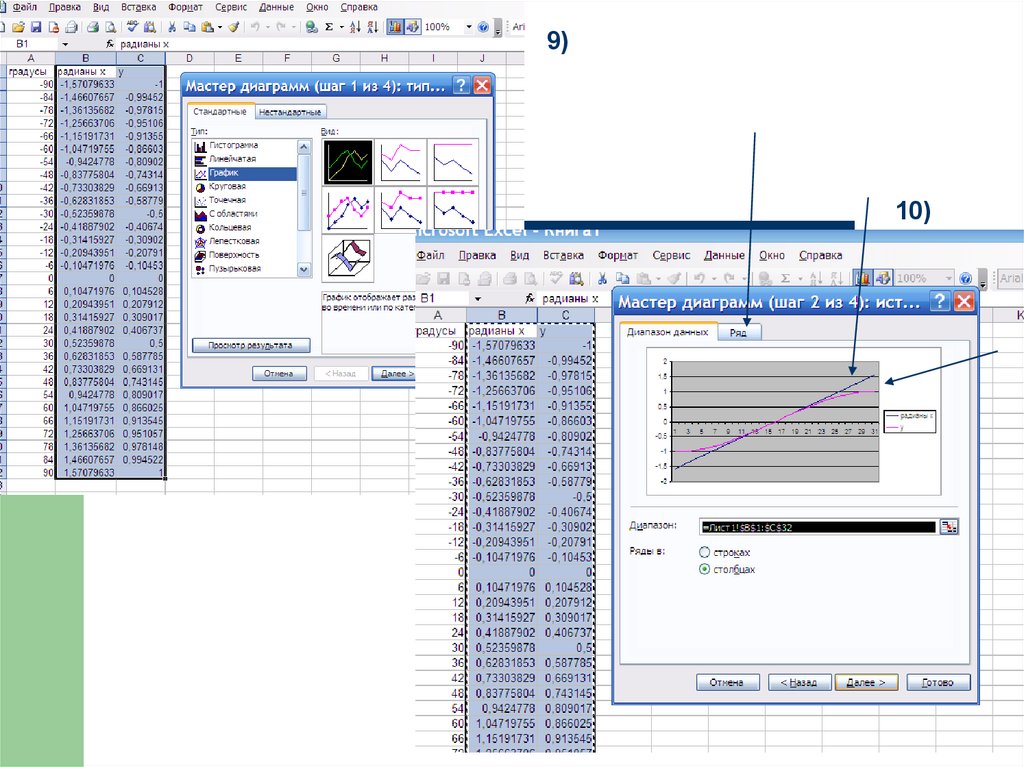
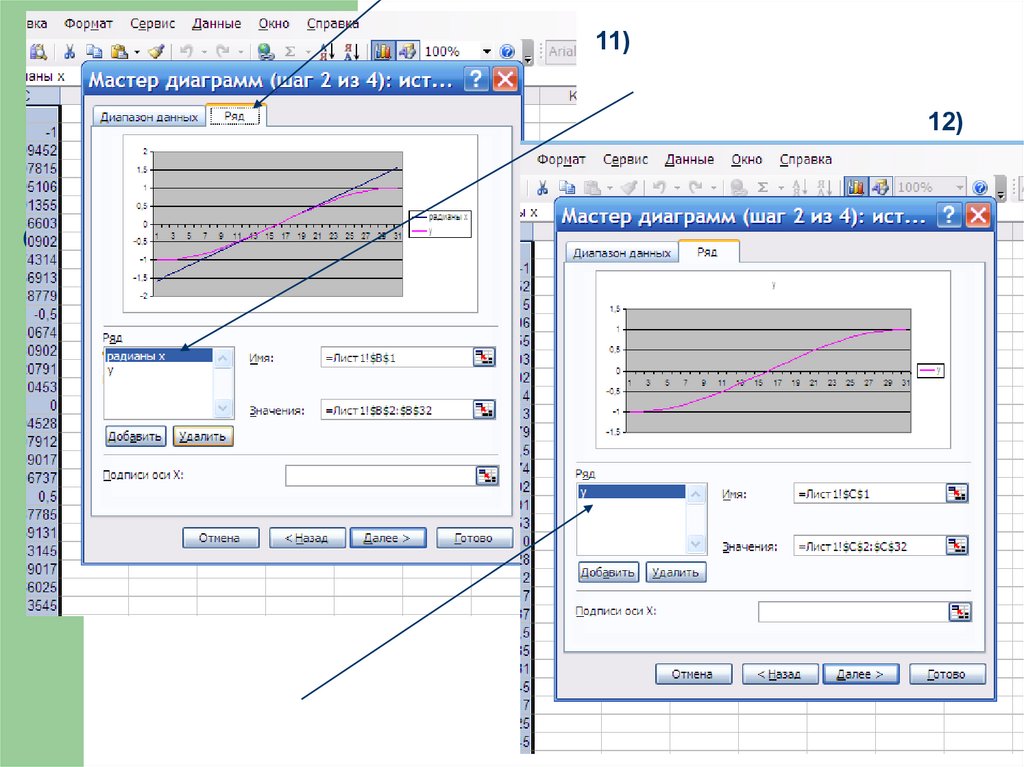
27)33. Задания:построить в Excel график функции
1) y sin( x )2) y sin x
3) y sin( x )
4) y 2 sin( x )
1
cos( x )
2
x
6) y sin( )
2
5) y
7 ) y cos( x
8) y sin( x
6
9) y sin( x )
6
)
)











 Математика
Математика Информатика
Информатика