Похожие презентации:
Действия с натуральными числами понятие степени
1.
ДЕЙСТВИЯ С НАТУРАЛЬНЫМИ ЧИСЛАМИПОНЯТИЕ СТЕПЕНИ .
2.
АнаграммаКлючевое слово поможет сформулировать тему урока!
подсказка
3.
Вычисляем более коротким способомВЫ УЗНАЕТЕ
Что означают записи вида 34
Как называются такие выражения и как вычисляют
их значение
51 + 51 + 51 + 51
В каких выражениях можно
одно действие заменить
35 + 35 + 35 + 35 + 35 другим?
Запишите полученные
7 ∙ 13 + 37 ∙ 7
выражения.
Что обозначает каждое число в
175 : 25
записи действия?
Сегодня вы научитесь
выполнять еще одну замену.
4.
Степень числаВы знаете, что сумму, в которой все слагаемые равны, можно
записать короче – в виде произведения. Часто приходится
вычислять и произведения, в которых все множители равны. В
математике также есть специальный способ для более короткой
записи таких произведений.
Понятие степени Рассмотрим примеры.
1) Чему равна площадь квадрата со стороной 5 см?
Чтобы ответить на этот вопрос, надо найти значение
произведения 5 ∙ 5. Его можно записать короче: 52.
2) Сколько стеклянных шариков поместится в коробку,
если каждый слой шариков состоит из 5 рядов, по 5 шариков в
каждом, и в коробку помещается 5 таких слоев? Для ответа на этот
вопрос надо вычислить произведение 5 ∙ 5 ∙ 5. Его можно записать
так: 53.
5.
Степень числаТочно так же произведение четырех множителей, каждый мз
которых равен 5, записывают в виде 54:
Рассмотрим последнее из этих выражений: 54. В этом
выражении число 5 — основание степени, а число 4 —
показатель степени. Основание степени — это повторяющийся
множитель, а показатель степени равен числу «повторений»,
т.е. он указывает, сколько одинаковых множителей содержится
в произведении. Читают выражение 54 так: «Пять в четвертой
степени».
6.
Степень числаСтепенью числа называют его
многократное произведение на
себя. Само число называют
основанием степени, а
количество его повторений в
произведении – показателем
степени.
7.
Степень числаЧтобы найти значение выражения 54, или, как говорят иначе,
возвести 5 в четвертую степень, надо вычислить произведение
5 ∙ 5 ∙ 5 ∙ 5. Получим 54 = 625.
Вторую степень числа называют также квадратом
этого числа. Например, запись 32 читают так: « Три во
второй степени» или «Три в квадрате».
32 = 3 ∙ 3 = 9.
Третью степень числа называют кубом этого числа.
Так, запись 43 читают: «Четыре в третьей степени» или
«Четыре в кубе».
43 = 4 ∙ 4 ∙ 4 = 64.
8.
Понятие степениЗапишите короче сумму и
произведение:
УЧЕБНИК
У: №175
а) 2 + 2 + 2 + 2, ?
2 ∙ 2 ∙ 2 ∙ 2; ?
в) а + а , ?
а∙а; ?
a∙2
a2
2∙4
24
8∙3
б) 8 + 8 + 8, ?
8∙8∙8;
г) b + b + b, ?
b ∙ b ∙ b;
83
?
?
b∙3
b3
9.
ПодумайЗапишите в виде степени:
УЧЕБНИК
У: №176
а) 3 ∙ 3; ?
б) 10 ∙ 10 ∙ 10; ?
32
в) 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4; ?
д) a ∙ a ∙ a ∙ a ∙ a ∙ a ∙ a; ?
е) n ∙ n ∙ n ∙ n;
?
г) 5 ∙ 5 ∙ 5 ∙ 5; ?
45
n4
a7
103
54
10.
ОбсудимВычислите :
УЧЕБНИК
У: №178
1) Обсудить возможность разных способов вычислений.
Например: 25 можно заменить произведением 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2,
а это можно заменить произведением 4 ∙ 4 ∙ 2 или 8 ∙ 4 и т.д.
а) 25; ?
32
б) 34; ?
81
в) 74; ?
2401
2) Дополнительные задания:
04;
?
0
13;
?
1
11.
СравниваемСравните значения выражений :
УЧЕБНИК
У: №179
а) 53 и 5 ∙ 3; ?
53 > 5 ∙ 3
в) 25 и 52;
25 > 52
?
д) 2 ∙ 2 и 22; ?
2 ∙ 2 = 22
12.
ВычисляемНайдите квадрат и куб числа:
УЧЕБНИК
У: №180
?
252 = 625; 253 = 15625;
б) 30; ?
302 = 900; 303 = 27000;
в) 50;
502 = 2500; 503 = 125000;
а) 25;
?
г) 100; ?
1002 = 10000; 1003 = 1000000;
13.
Найдем площадьЗапишите выражение для
нахождения площади квадрата со
стороной: 1см, 2дм, 10см, 12м.
В каждом случае найдите его
площадь.
УЧЕБНИК
У: №181
Образец. Найдем площадь квадрата со стороной 9см:
92 = 81(см2).
?
12 = 1(см2);
2дм; ?
22 = 4(дм2);
10см; ?
102 = 100(см2);
12м; ?
122 = 144(м2);
1см;
14.
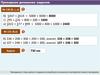
Выполняем упражненияСоставьте таблицу степеней с основаниями 2, 3, 4, 5:
22 =
23 =
24 =
25 =
26 =
4
8
16
32
64
32 = 9
? 33 = 27
? 34 = 81
?
?
?
42 = 16
43 = 64
?
?
52 = 25
53 = 125
?
?
?
?
?
В столбиках каждый следующий результат должны получать
умножением предыдущего результата соответственно на 2, на 3,
на 4 и на 5.
15.
Выполняем упражненияСоставьте таблицу степеней с основаниями 2, 3, 4, 5:
22 =
23 =
24 =
25 =
26 =
32 = 9 42 = 16 52 = 25
33 = 27 43 = 64 53 = 125
16 34 = 81
32
64
4
8
16.
Примерное выражениеХорошо известны различные виды
таблиц умножения.
Мы с вами составили фрагмент
таблицы возведения в степень.
Поясните используемую в таблице
степеней закономерность.
Домашнее задание
У: стр. 56 – 57 – читать (фрагмент «Понятие степени»),
рубрика «Вопросы и задания» (вопросы 1, 2); З: №121(а-г), 122,
123, 124, 128 (карандашом в задачнике; вычисления должны
выполняться без калькулятора); Т:№ 21(первая, вторая спирали).
















 Математика
Математика