Похожие презентации:
Ряды динамики
1.
Ряды динамики2.
Ряды динамикичисловые значения статистического показателя, расположенные в
хронологическом порядке и характеризующие развитие явления во
времени.
Составляющими элементами ряда динамики являются:
значения показателя – уровни ряда (обозначаются через y);
периоды или моменты времени, к которым относятся уровни
(обозначаются через t).
3.
Требования к сбору и анализу• Данные должны быть сопоставимы (иметь отношение к одному
объекту/типу данных):
• по территории,
• кругу охватываемых объектов,
• единицам измерения (в т.ч. ценам: деньги имеют цену),
• времени регистрации,
• методологии расчета.
4.
Ряды динамикиабсолютные
По формам выражения
показателя
относительные
средние
интервальные
По временной
определенности уровней
моментные
равностоящие
По расстоянию между
уровнями
неравностоящие
5.
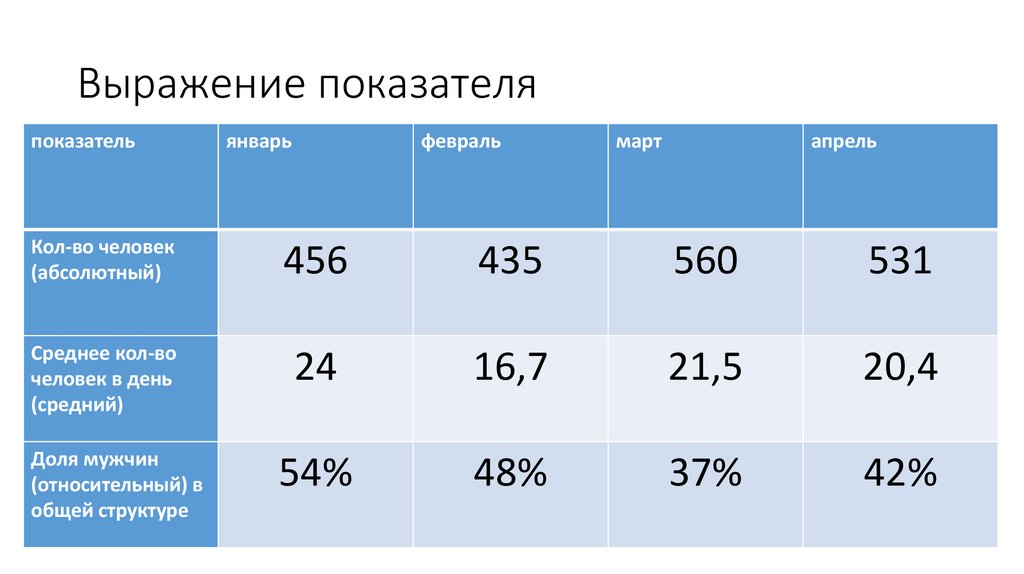
Выражение показателяпоказатель
январь
февраль
март
апрель
Кол-во человек
(абсолютный)
456
435
560
531
Среднее кол-во
человек в день
(средний)
24
16,7
21,5
20,4
Доля мужчин
(относительный) в
общей структуре
54%
48%
37%
42%
6.
Временная определенность уровнейМоментные – на определенный
момент времени – не кумулятивный
Интервальные – показатель за
определенный интервал (временной
промежуток) – чаще всего кумулятивный
Показатель удовлетворенности
Кол-во посетителей за период
5
600
560
4,5
500
4
3,5
456
531
435
400
3
2,5
300
2
200
1,5
1
100
0,5
0
0
1 кв.
2 кв.
3 кв.
Показатель удовлетворенности
4 кв.
1 кв.
2 кв.
3 кв.
Кол-во посетителей за период
4 кв.
7.
По расстоянию между интерваламиРавностоящий
Неравностоящий
Показатель удовлетворенности
Показатель удовлетворенности
5
4,6
4,5
4,4
4
3,5
4,2
3
2,5
4
2
3,8
1,5
1
3,6
0,5
0
3,4
1 кв.
2 кв.
3 кв.
Показатель удовлетворенности
4 кв.
1 кв.
3 кв.
Показатель удовлетворенности
4 кв.
8.
Простые аналитические показатели• Абсолютный прирост;
• Темп роста и темп прироста;
• Абсолютное значение 1% прироста.
9.
Сравнение данных внутри одного ряда• Принято сравниваемый уровень называть отчетным, а уровень,
с которым производят сравнение - базисным.
• Возможны два способа сравнения уровней ряда динамики:
• Расчет базисных показателей, при котором все уровни ряда
сравниваются с фиксированным уровнем – базисным. Обычно
за базисный берется начальный (первый) уровень.
• Расчет цепных показателей, при котором каждый
последующий уровень ряда динамики сравнивается с
предыдущим.
10.
Абсолютный прирост (∆) - характеризует размер увеличения (илиуменьшения) уровня ряда за определенный промежуток времени.
Базисный
б yi y1
где
Цепной
ц yi yi 1
у1 - уровень базисного периода;
yi - уровень i-го периода;
yi-1 - уровень ряда, предшествующий i-му уровню ряда динамики.
11.
Темп роста (Тр) – показывает отношение изменения текущегоуровня ряда к предыдущему или базисному.
Базисный
Цепной
yi
yi
100%
Т р 100% Т р
y i 1
y1
Темп роста м.б. выражен в виде коэффициента. Показывает, во
сколько раз данный уровень ряда больше уровня предшествующего
или базисного или какую его часть он составляет.
12.
Темп прироста (Тпр) – показывает на какой процент (долю)уровень данного периода больше (меньше) базисного.
Базисный
Цепной
б
Т пр
100%
y1
ц
Т пр
y i 1
100%
Т пр Т р 100% Т пр Т р 100%
13.
Абсолютное значение 1% прироста (А) – показывает, сколькоабсолютных единиц приходится на 1% прироста (уменьшения).
Только для цепных показателей!!! (Эффект низкой базы)
ц
А
Т пр
А 0,01 yi 1
14.
Средние аналитические показатели в рядахдинамики
• Метод расчета среднего уровня ряда динамики зависит от вида
временного ряда.
• Для интервального ряда абсолютных показателей с равными
интервалами средний уровень за определенный период
определяется по формуле простой арифметической:
yi
y
n
15.
Средние аналитические показатели в рядахдинамики
• Средний уровень моментного динамического ряда, если
интервалы между датами равны, рассчитывается по формуле
средней хронологической:
y
1
2
y1 y 2 ... y n 1 y n
n 1
1
2
16.
Средние аналитические показатели в рядахдинамики
Для определения среднего уровня моментного ряда с
неравномерными промежутками между временными датами
вычисляется средняя арифметическая взвешенная. В качестве
весов принимается продолжительность промежутков времени
между моментами, в которые происходят изменения в уровнях
динамического ряда:
y *t
y
t
i
i
i
17.
средний уровень моментного ряда снеравномерными промежутками
1-2 кв.
Показатель
удовлетворенности
3 кв.
4,3
4 кв.
4,8
Ср. ур. = (4,3*2 + 4,8*1 + 4,4*1)/4 = 4,45
4,4
18.
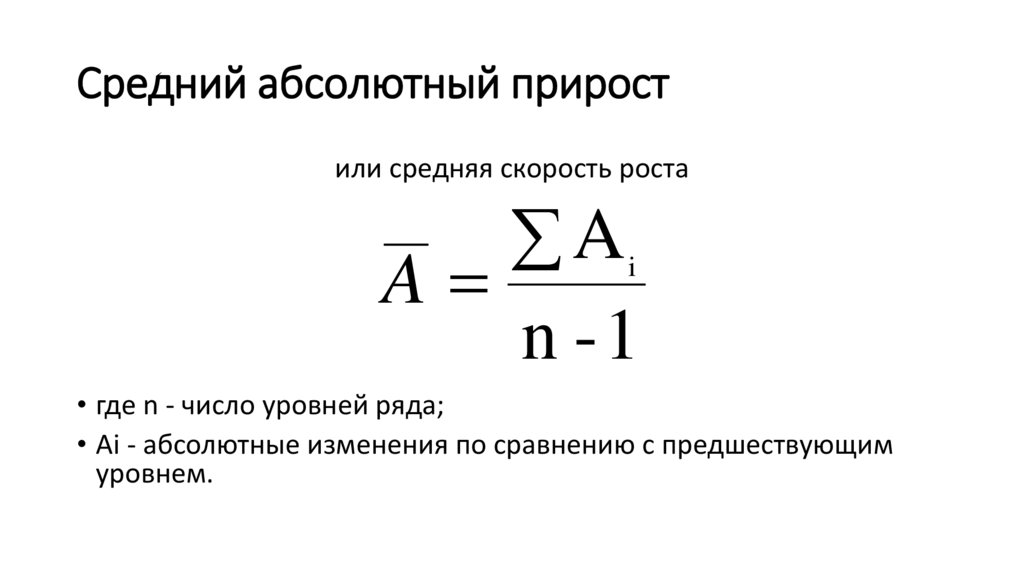
Средний абсолютный приростили средняя скорость роста
A
A
n -1
i
• где n - число уровней ряда;
• Аi - абсолютные изменения по сравнению с предшествующим
уровнем.
















 Математика
Математика








