Селекция3а

1.

Теория селекции
Лекция 3. QTL – Quantitative Trait Loci
локусы количественных признаков
В.М.Ефимов, д.б.н.
Институт цитологии и генетики СО РАН

2. Примеры

• Двоичные признаки
– присутствие/ отсутствие болезни
• Количественные признаки
– Давление крови
– Время выживания
– Масса опухоли
– И т.д.

3.

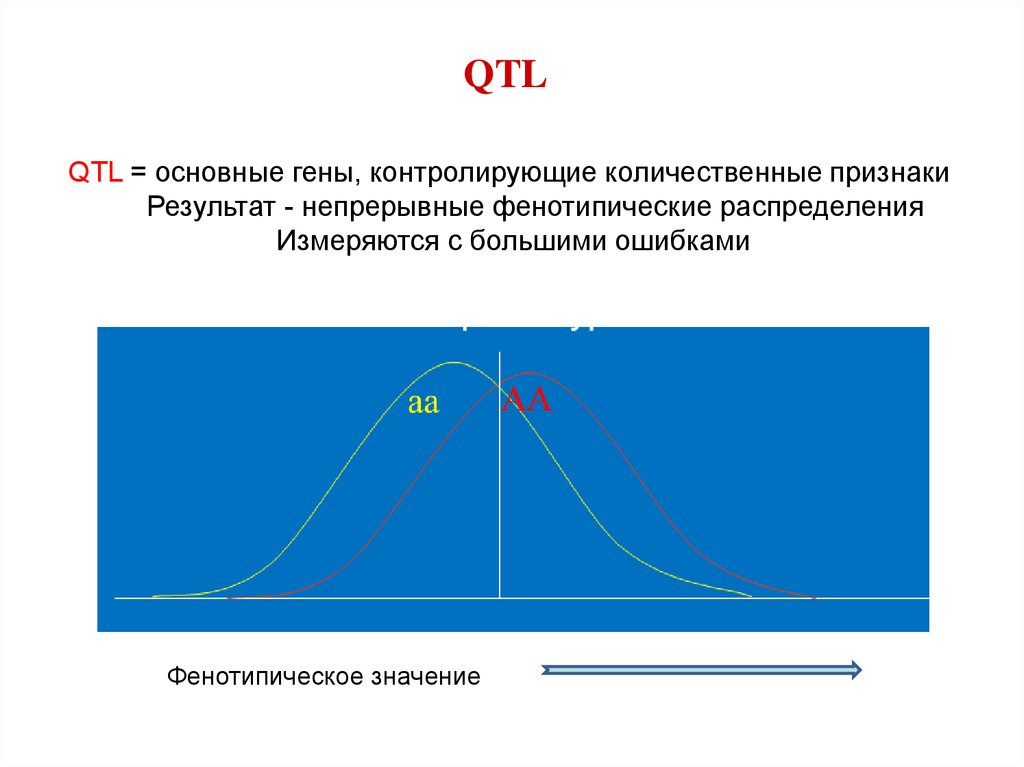
QTL
QTL = основные гены, контролирующие количественные признаки
Результат - непрерывные фенотипические распределения
Измеряются с большими ошибками
Фенотипическое значение

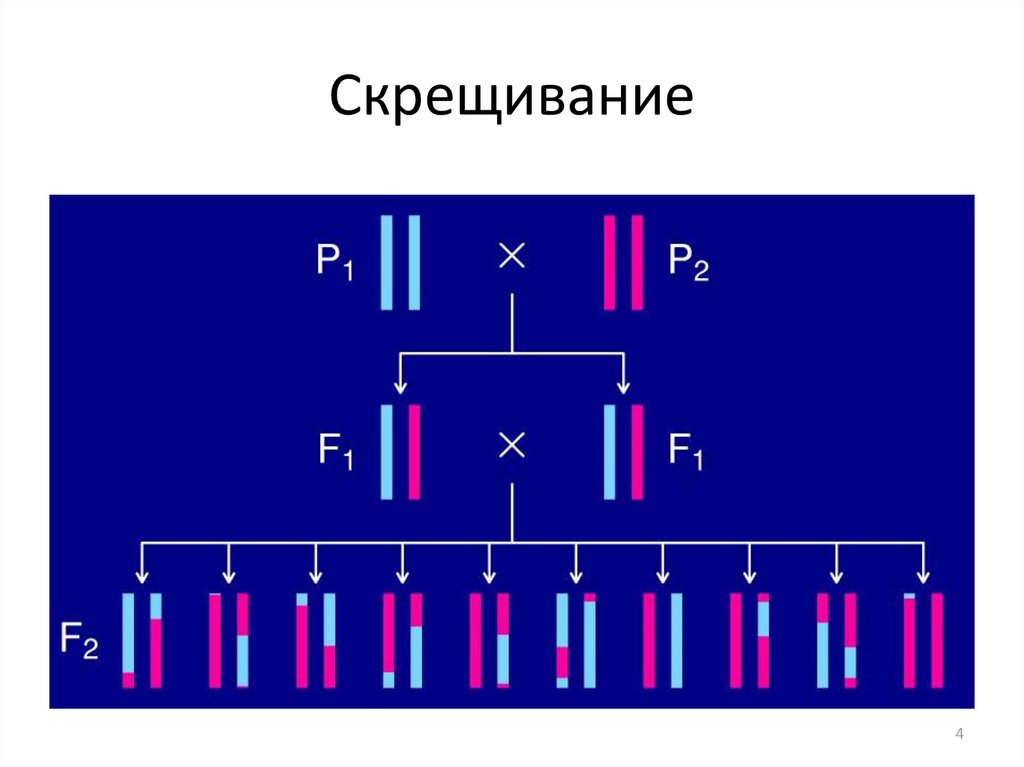
4. Скрещивание

4

5. P1 -- NOD

5

6. P2 -- C57BL/6

6

7. F1 -- Agouti coat

7

8. Скрещивание

P1
F1
F2
X
X
P2
F1

9. Распределение Y : один двуаллельный локус

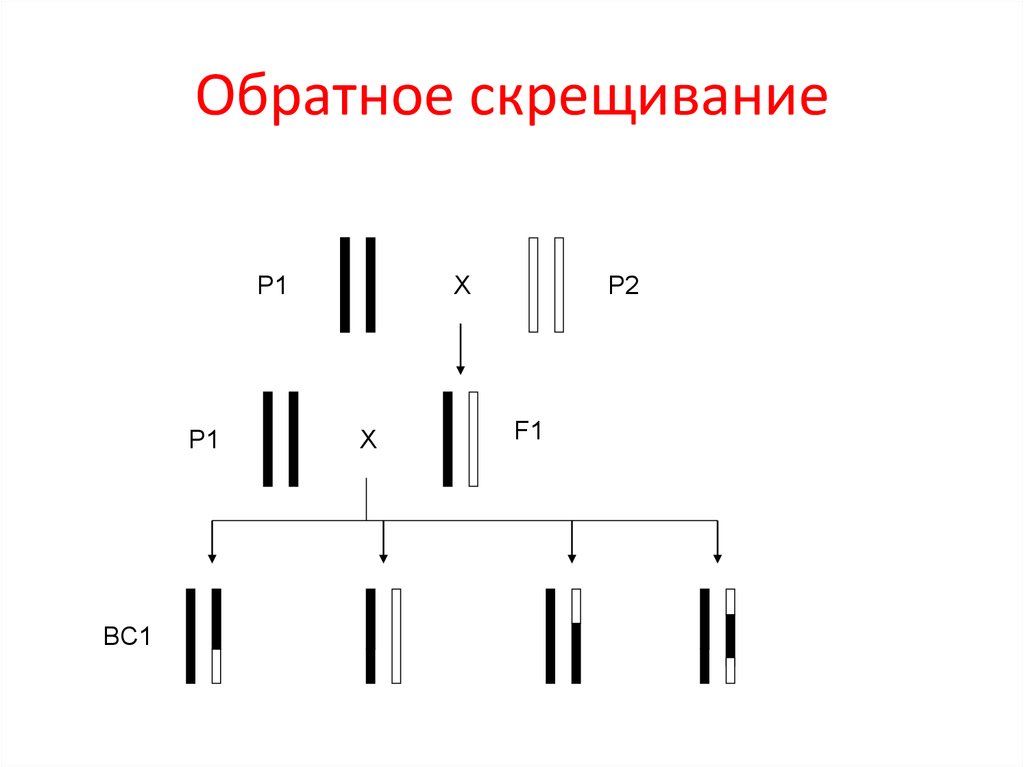
10. Обратное скрещивание

P1
P1
BC1
X
X
P2
F1

11.

QTL
АА и аа индивидуумы могут визуально не
различаться
Некоторые линии АА будут иметь низкое
значение признака из-за влияния среды или
других генов
Некоторые линии aa будут иметь высокое
значение признака из-за влияния среды или
других генов

12.

QTL. Эффект
Аддитивный эффект одного аллеля QTL = a
Среднее значение признака в F1
от скрещивания между родителями
AA и aa = B
Среднее значение для линий AA равно B + a
Среднее значение для линий aa равно B - a

13. Графически

14.

QTL. Эффект
Маркеры ДНК могут быть использованы
для картирования полезных генов с использованием
частот рекомбинации связанных генов:
Маркеры возле QTL косегрегируют с ним
Маркеры, тесно связанные с QTL, обнаруживаются ANOVA
Большинство гамет из F1 -- AM или am.
Кроме того, при скрещивании маркера и QTL
будут произведены гаметы Am и aM

15.

QTL. Эффект
Таким образом, R -- эффект маркера М
является функцией:
(1) расстояния от QTL
(2) размера эффекта QTL

16.

QTL. Эффект
Линии ММ легко отделяются от линий mm,
но линии АА нельзя отличить от линий aa
Если М и А связаны, то среднее значение ММлиний будет отличаться от среднего значения в
мм-линиях
Разность может изменяться от 0 до a,
в зависимости от расстояния между маркером и
QTL
Средние ММ и мм рекомбинантных инбредных
линий:
MM = B + a (1-2R)
mm = B - a (1-2R)

17. Картирование QTL с помощью молекулярных маркеров

Маркеры ДНК применяются для картирования полезных
генов с использованием частот рекомбинации
связанных генов:
M1
A
M2
m1
a
m2
• Маркеры возле QTL косегрегируют с ним
• Маркеры, тесно связанные с QTL, обнаруживаются ANOVA

18. Стратегии картирования QTL

Все эксперименты по картированию на основе
маркеров имеют одну и ту же основную стратегию:
Выбор родителей, отличающихся по признаку
Сканирование двух родителей для полиморфных маркерных
локусов
Получение рекомбинантных инбредных линий
(могут использоваться линии, полученные из F2)
Сканирование фенотипов
Вычисление средних между ММ- и мм-линиями
для каждого локуса
Нахождение QTL с наибольшим (ММ-мм)

19. Одномаркерный анализ

Выбор родителей, отличающихся по признаку
Сканирование двух родителей для полиморфных
маркерных локусов
Получение рекомбинантных инбредных линий
(могут использоваться линии, полученные из F2)
Оценка фенотипов
Дисперсионный анализ влияния каждого маркера
Нахождение QTL со значимым F-критерием
IRRI: Planning Breeding Programs for
Impact

20. Стратегия картированияQTL: одномаркерный анализ

200
QTL?
Разница
средних
MM – mm
линий
QTL?
• ANOVA делается для
каждого маркера
• QTL выявляется, если
t-критерий значим
100
0
20
40
60
80
Позиция на карте (cM)
100
120

21.

Измерение вклада QTL в σP2
Простейшая модель QTL делит генотипический
эффект на эффект QTL (A) и влияние всех
других генов в классах QTL(G(QTL)):
Y=m + G +
e
= m + G(QTL) + A + e
IRRI: Planning Breeding Programs for
Impact

22.

Измерение вклада маркера в σP2
Y=m + G +
e
= m + G(M) + M + e
IRRI: Planning Breeding Programs for
Impact

23. Наследуемость в широком смысле для эксперимента, в котором обнаружен один QTL

=
hG2
σ2G
σ 2P
=
σ2G(QTL) + σ2A
σ2G(QTL) + σ2A + (σ2e /r)

24. Наследуемость в узком смысле (аддитивная) для эксперимента, в котором обнаружен один QTL

=
hA2
σ2A
σ 2P
=
σ 2A
σ2G(QTL) + σ2A + (σ2e /r)

25. Стратегия картированияQTL: одномаркерный анализ

Проблемы с одномаркерным анализом:
Плохая точность определения позиции QTL изза рекомбинации между маркером и QTL
Применение t-теста к каждому маркеру
приводит к множеству ложно-позитивных
выводов (это общая проблема QTL)

26. Стратегия картирования QTL: интервальное картирование

Маркируемый интервал = интервал между двумя
маркерами
Методы отображения интервалов используют
информацию о значениях двух обрамляющих
маркеров для оценки положения QTL
Вычисляется вероятность того, что данные могут
быть получены в предположении, что QTL
расположен между маркерами
Считается, что QTL находится в позиции, при
которой вероятность получения наблюдаемых
данных самая высокая

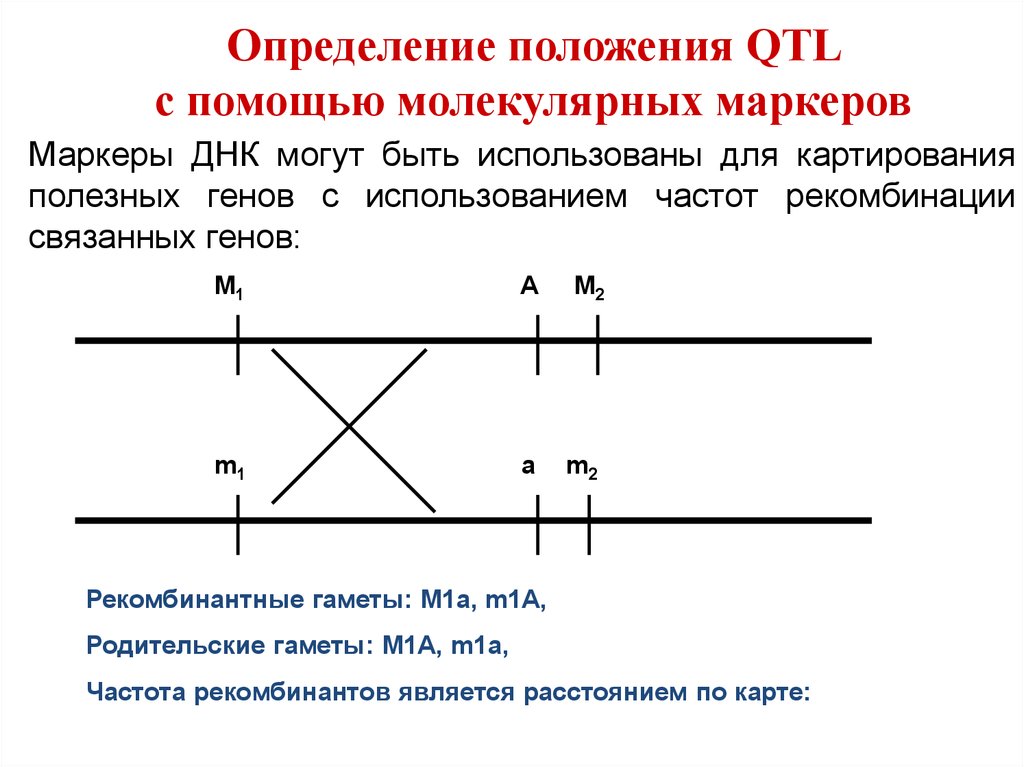
27. Определение положения QTL с помощью молекулярных маркеров

Маркеры ДНК могут быть использованы для картирования
полезных генов с использованием частот рекомбинации
связанных генов:
M1
A
M2
m1
a
m2
Рекомбинантные гаметы: M1a, m1A,
Родительские гаметы: M1A, m1a,
Частота рекомбинантов является расстоянием по карте:

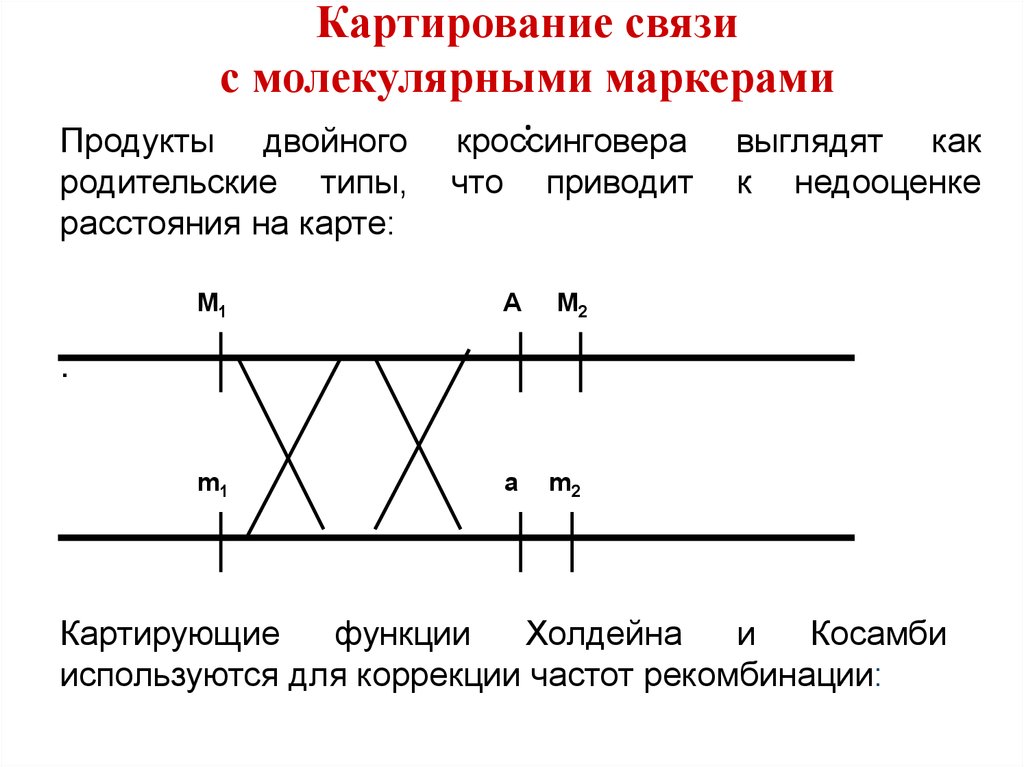
28. Картирование связи с молекулярными маркерами :

Продукты двойного кроссинговера
выглядят
родительские типы,
расстояния на карте:
что
приводит
M1
A
M2
m1
a
m2
к
как
недооценке
:
Картирующие
функции
Холдейна
и
Косамби
используются для коррекции частот рекомбинации:

29. Стратегия картирования QTL: интервальное картирование

Тест значимости:
Логарифм отношения шансов (оценка LOD=lg(OD)):
Вероятность появления данных с QTL
OD =
Вероятность появления данных без QTL
• LOD 2 означает, что 100 раз более вероятно, что QTL находится в
данном интервале, чем то, что там его нет
• LOD 3 означает, что в 1000 раз более вероятно, что QTL находится в
: данном интервале, чем то, что там его нет

30. Тонкое картирование

Для того, чтобы быть полезным в реальной селекции,
интересующий нас ген должен быть тесно связан с
маркером
В идеале сам ген используется в качестве маркера

31. Резюме

QTL картирование -- локализация генов, влияющих
на
количественные
признаки,
используя
молекулярные маркеры
Стратегии картирования QTL
основаны на
измерении средней разницы между линиями с
контрастирующими маркерными аллелями
QTL картирование -- предварительный шаг в
обнаружении полезных генов с помощью маркерориентированного обратного скрещивания

32. Резюме

До сих пор только успешные гены устойчивости к
болезням и стрессоустойчивости имели очень
большие эффекты
QTL картирование -- базовая исследовательская
деятельность, требующая тщательного планирования
скрещиваний и высокоточного фенотипирования

33.

Литература
Kearsey, M.J. and Pooni, H.S. 1996. The genetical
analysis of quantitative traits. Chapter 7.
Bernardo, R. 2002. Breeding for quantitative traits in
plants. Chapters 13 and 14.

34.

Многомерная наследуемость

35.

Многомерный аналог коэффициента наследуемости
Lande R (1979). Quantitative genetic analysis of multivariate
evolution applied to brain:body size allometry. Evolution 33:402–416.
H = GP-1
G – матрица коэффициентов корреляции между родителями и потомками
P – фенотипическая матрица корреляций между признаками
Уравнение селекционера
Smith, H.F. 1936. A discriminant function
for plant selection. Ann. Eugen. 7: 240-250.
s – селекционный дифференциал
∆µ – ответ на отбор
∆µ = GP-1s = Hs

36.

Родители (X)
Потомки (Y)
X11
X12
…
X1,M-1
X1,M
Y11
Y12
…
Y1,M-1
Y1,M
X21
X22
…
X2,M-1
X2,M
Y21
Y22
…
Y2,M-1
Y2,M
X31
X32
…
X3,M-1
X3,M
Y31
Y32
…
Y3,M-1
Y3,M
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
XN-2,1
XN-2,2
…
XN-2,M-1
XN-2,M
YN-2,1
YN-2,2
…
YN-2,M-1
YN-2,M
XN-1,1
XN-1,2
…
XN-1,M-1
XN-1,M
YN-1,1
YN-1,2
…
YN-1,M-1
YN-1,M
XN,1
XN,2
…
XN,M-1
XN,M
YN,1
YN,2
…
YN,M-1
YN,M
P = RX/X
G = RX/Y

37.

Поиск осей с максимальной наследуемостью
(в узком смысле)
Ott J, Rabinowitz D (1999). A principal-components approach
based on heritability for combining phenotype information.
Hum Hered 49: 106–111.
Klingenberg CP, Leamy L. 2001. Quantitative genetics
of geometric shape in the mouse mandible.
Evolution 55(11): 2342–2352.
∆µ = GP-1s = Hs = λs

38.

Многомерная наследуемость
Расположение центроидов родительских и гибридных выборок
в многомерном пространстве признаков
при аддитивно-доминантной модели наследования
F1 - m – ось гетерозиготности;
P1 - P2 – ось аддитивности
Heredity, 2005. V. 94. P. 101-107.

39.

Многомерная наследуемость
Расположение центроидов родительских и гибридных выборок
в многомерном пространстве признаков в общем случае
(HIA-модель)
F1 - F# – ось гетерозиготности H
P1 - P2 – ось аддитивности A
m - F# – ось эпистаза I
(F1 - m – ось гетерозиготности
в аддитивно-доминантной модели)

40.

Материал

41.

42.

Родственные связи

43.

Родственные связи

44.

Коэффициенты корреляции родителей с потомками
по первым пяти компонентам
с максимальной аддитивной наследуемостью
(выделены достоверные при p<0.05; N=196)
Descedants
Parents
Factor1
Factor2
Factor3
Factor4
Factor5
Factor1
0.66
0.05
0.06
-0.04
0.02
Factor2
-0.06
0.35
0.15
-0.09
0.06
Factor3
-0.09
-0.12
0.32
0.08
0.02
Factor4
0.00
0.06
-0.06
0.14
0.09
Factor5
-0.06
-0.06
-0.01
-0.10
0.03

45.

Коэффициент наследуемости
через корреляции “родитель-потомок”:
h 2r
2
один родитель - потомок
(в случае отсутствия ассортативности)
2r
h
1 a
2
(при ассортативности)
один родитель - потомок

46.

Расположение семей на плоскости первых двух компонент
аддитивной наследуемости

47.

Корреляция между родителями и детьми
по первой компоненте аддитивной наследуемости

48.

Корреляция между родителями (ассортативность)
по первой компоненте аддитивной наследуемости

49.

Корреляция между дедушками и бабушками
по первой компоненте аддитивной наследуемости

50.

Корреляция между родителями (два поколения)

51.

После учета ассортативности выявилось,
что четыре компоненты шкалирования
имеют значимые коэффициенты наследуемости
Factor1 Factor2 Factor3 Factor4
Factor5
r
0.66
0.35
0.32
0.14
0.03
ρa
0.75
0.42
0.29
-0.3
0.75
h2
0.75
0.49
0.50
0.40
0.03

52.

Спасибо за внимание!