Похожие презентации:
Многоугольник
1. Многоугольник
2.
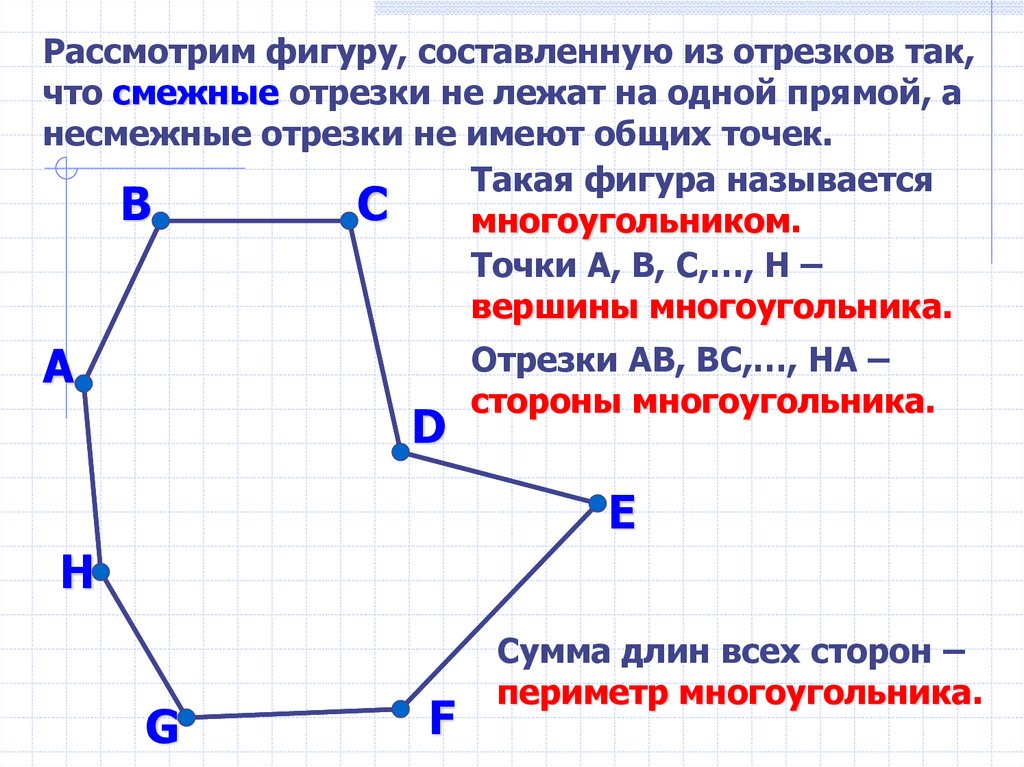
Рассмотрим фигуру, составленную из отрезков так,что смежные отрезки не лежат на одной прямой, а
несмежные отрезки не имеют общих точек.
Такая фигура называется
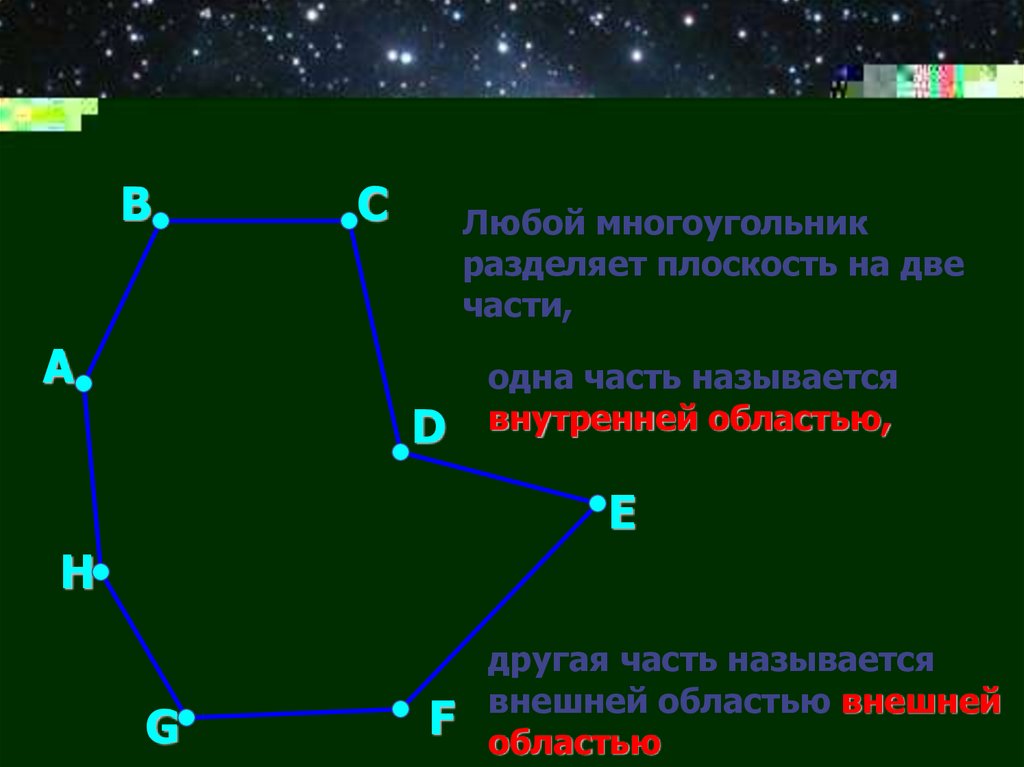
В
С
многоугольником.
Точки А, В, С,…, H –
вершины многоугольника.
А
D
Отрезки АВ, ВС,…, HА –
стороны многоугольника.
E
H
G
F
Сумма длин всех сторон –
периметр многоугольника.
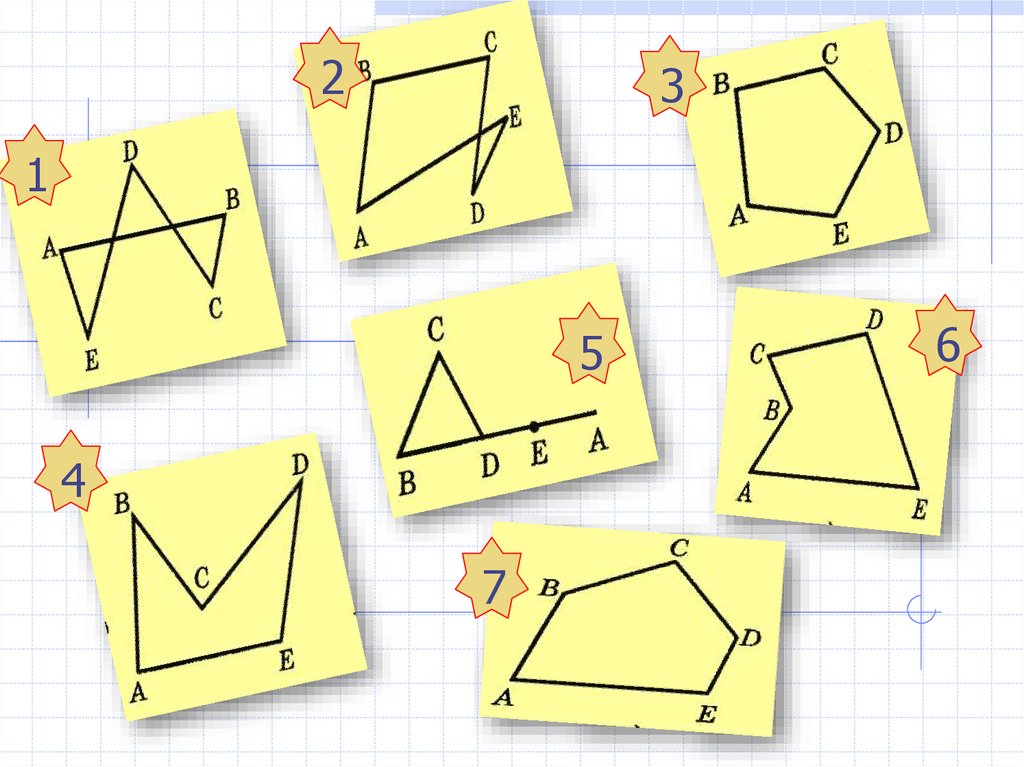
3.
23
1
5
4
7
6
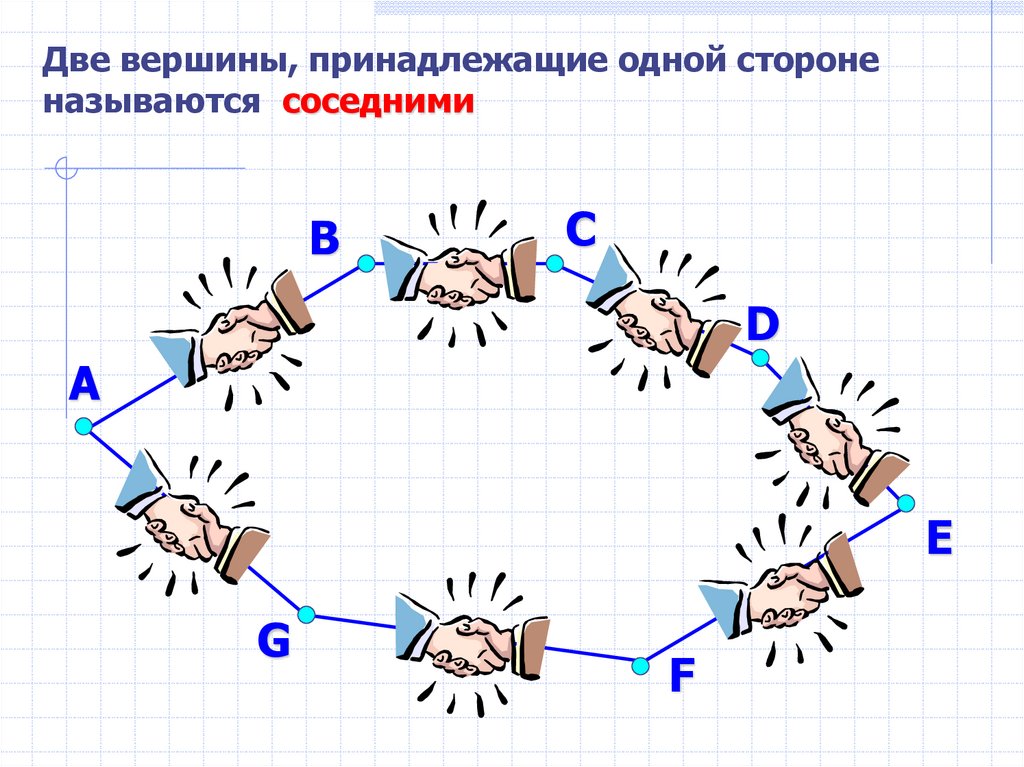
4.
Две вершины, принадлежащие одной стороненазываются соседними
В
С
D
А
E
G
F
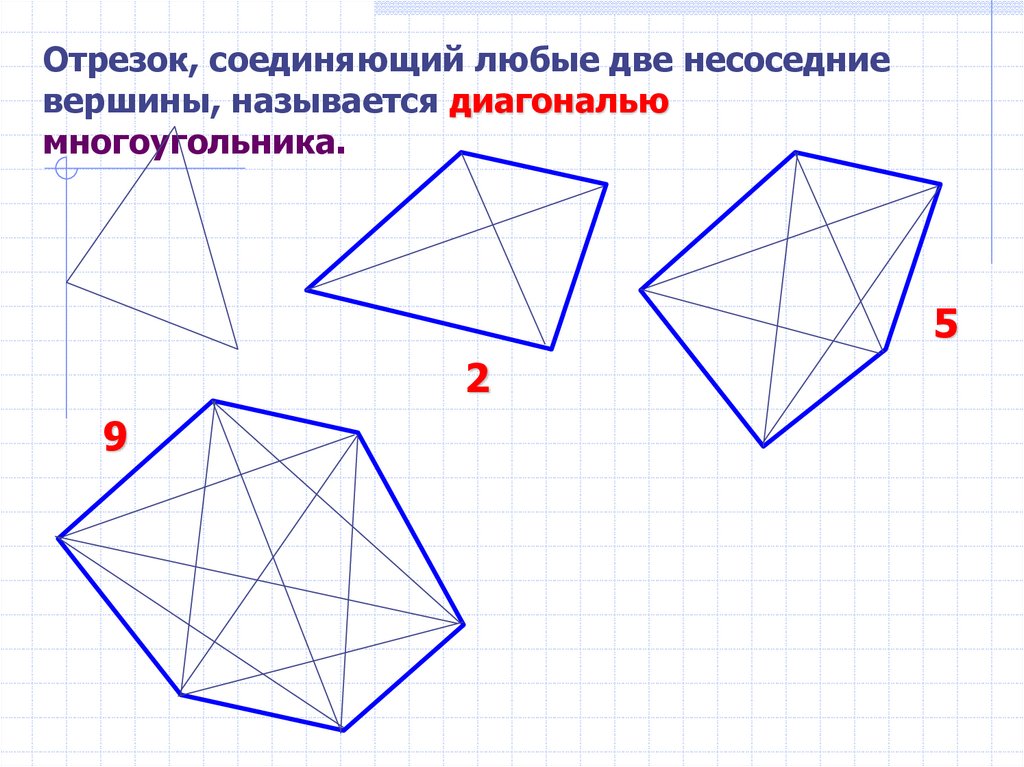
5.
Отрезок, соединяющий любые две несоседниевершины, называется диагональю
многоугольника.
5
2
9
6. Диагонали многоугольника
А1 А2 , А 1 А4 –диагонали
многоугольника.
Число диагоналей
из одной вершины
n-3
7.
ВС
Любой многоугольник
разделяет плоскость на две
части,
А
D
одна часть называется
внутренней областью,
E
H
G
F
другая часть называется
внешней областью внешней
областью
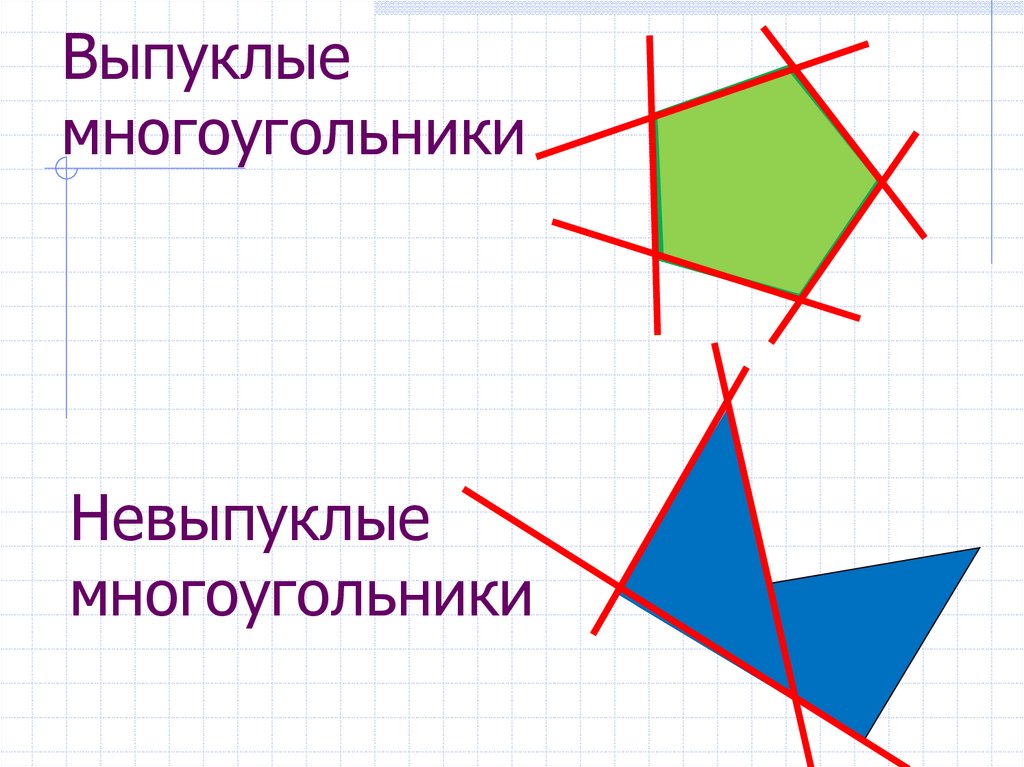
8. Выпуклые многоугольники
СА
В
F
D
9. Выпуклые многоугольники
Невыпуклыемногоугольники
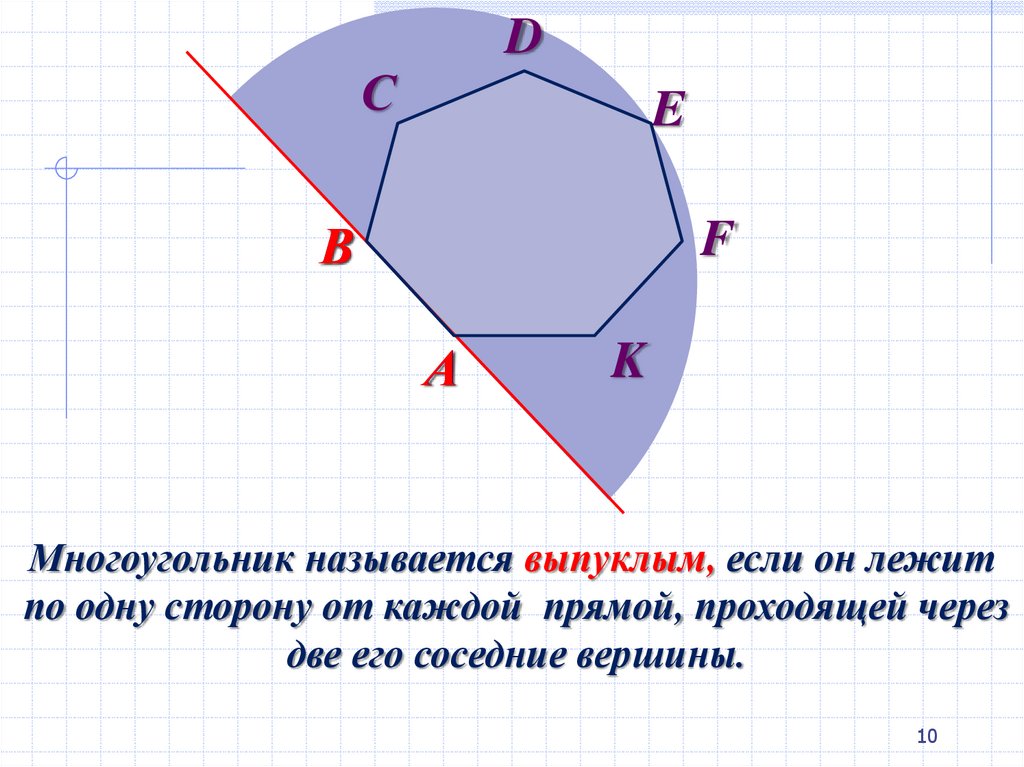
10.
DС
E
В
F
А
K
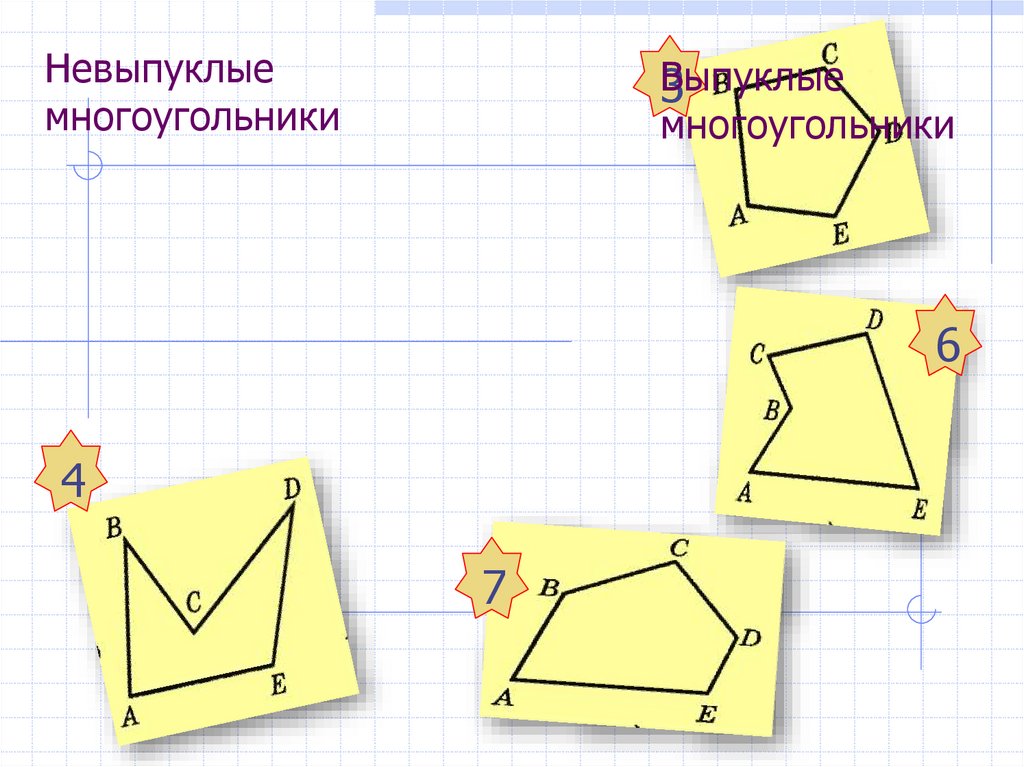
Многоугольник называется выпуклым, если он лежит
по одну сторону от каждой прямой, проходящей через
две его соседние вершины.
10
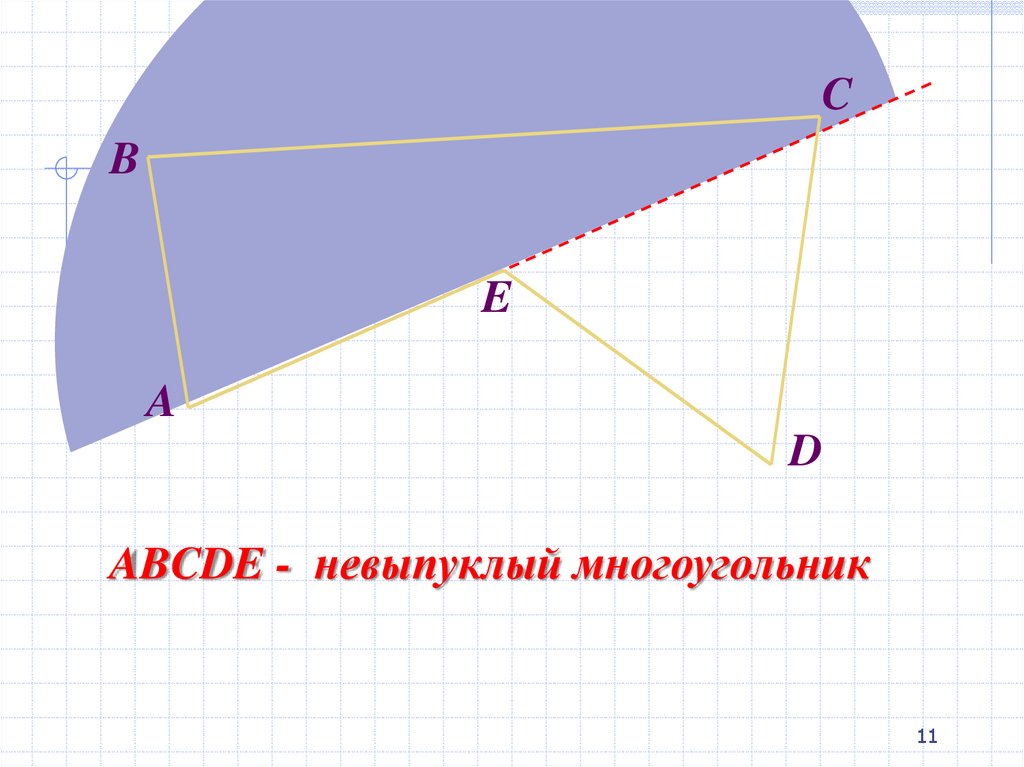
11.
CB
E
A
D
ABCDE - невыпуклый многоугольник
11
12. Практическая работа
Количество угловмногоугольника
Количество
получившихся
треугольников
Сумма углов
многоугольника
4
5
6
2
3
4
180∙2 180∙3 180∙4
13.
ЗадачаСколько сторон имеет многоугольник, если каждый угол
которого равен 120°.
1
Решение
Обозначим п – количество сторон многоугольника.
Так как сумма углов выпуклого многоугольника
(п – 2) · 180°.
То следовательно (п – 2) · 180° = 120° · п
180° · п - 360° = 120° · п
60° · п = 360°
п = 360° : 60°
Ответ: 6 сторон.
п=6
13
14.
Задача2
Найти стороны четырехугольника, если его периметр 66 см,
первая сторона больше второй на 8 см и на столько же
меньше третей, а четвертая - в три раза больше второй.
B
A
Решение
x
С
х + x – 8 + х + 8 + 3х – 24 = 66
6х – 24 = 66
6х = 66 + 24
6х = 90
х = 90 : 6
х = 15
ВС = 15 см, AB = 15 – 8 = 7 см,
CD = 15 + 8 = 23 cм,
AD = 3· 7 = 21 см.
Периметр это сумма
D
длин всех сторон,
поэтому:
х + (x – 8) + (х + 8) + 3(х – 8) = 66 Ответ: 15 см, 7 см, 23 cм, 21 см.
14
15.
Дано:АВСD – четырехугольник, ∠А = ∠B =∠C =∠D
Найти:
B
A
3
∠А -?
С
Решение
По формуле о сумме углов
многоугольника имеем:
D
(п – 2)·180° = (4 – 2)·180° = 360°
По условию ∠А = ∠B =∠C =∠D,
следовательно ∠А = 360° : 4 = 90°
Ответ: 90°
15
16.
Дано:Найти:
B
4
АВСD – четырехугольник,
∠А:∠B:∠C:∠D = 1:2:4:5
∠А,∠B, ∠C, ∠D - ?
С
Решение
∠А + ∠B + ∠C + ∠D = 360°
Пусть ∠А = х
тогда ∠B = 2х, ∠C = 4х, ∠D = 5х
х + 2х + 4х + 5х = 360°
A
12х = 360°
D
х = 360° : 12
х = 30°
∠А = 30°, ∠B = 2х = 60°, ∠C = 4х = 120°, ∠D = 5х = 150°
Ответ: 30°, 60°, 120°, 150°
16
17.
В равнобедренном треугольнике АВС соснованием АС, внешний угол при вершине С
равен 1230. Найдите величину угла АВС. Ответ
дайте в градусах.
В
А
С
18.
Невыпуклыемногоугольники
Выпуклые
3
многоугольники
6
4
7
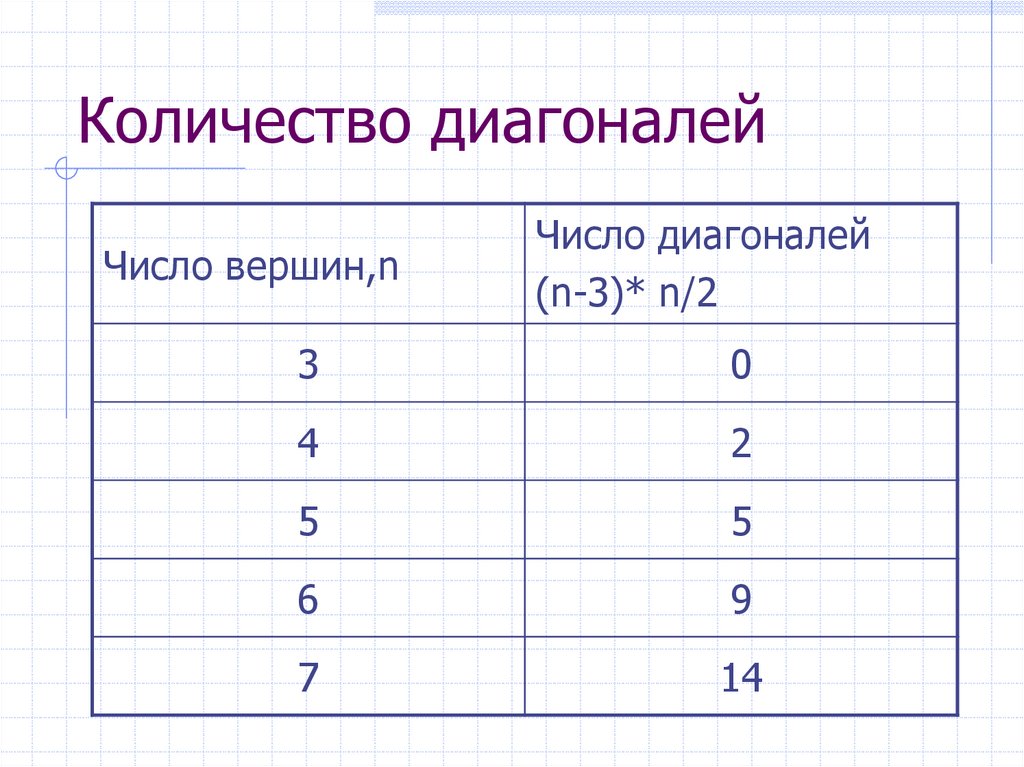
19. Количество диагоналей
Число вершин,nЧисло диагоналей
(n-3)* n/2
3
0
4
2
5
5
6
9
7
14
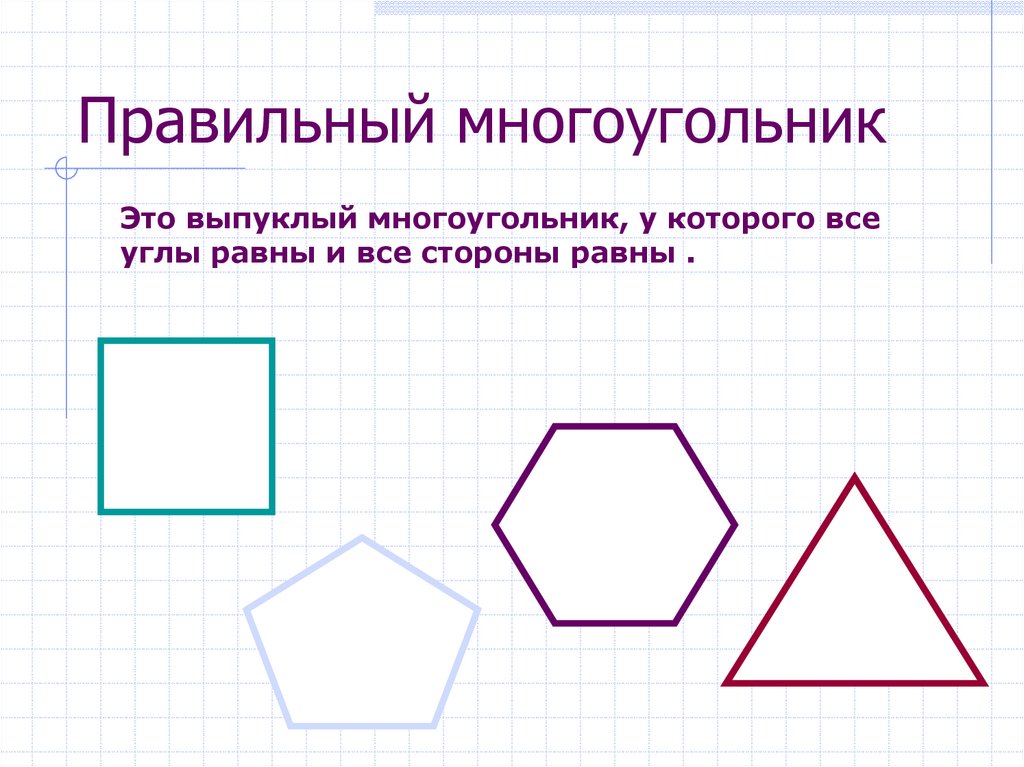
20. Правильный многоугольник
Это выпуклый многоугольник, у которого всеуглы равны и все стороны равны .
21. Правильные многоугольники
все углы равнывсе стороны равны
все углы равны и все стороны равны










 Математика
Математика








