Система уравнений ГД и разностные схемы для ее решения

1.

Нелинейные вычислительные процессы
Семинар № 5
Система уравнений газовой
динамики и разностные схемы
для ее решения
к.ф.-м.н. Уткин Павел Сергеевич
e-mail: utkin@icad.org.ru, pavel_utk@mail.ru
(926) 2766560
7 марта 2014 г., МФТИ, Долгопрудный

2.

Краткое содержание предыдущих семинаров
Семинар № 1 (07.02.14). Некоторые разностные
схемы для решения линейного уравнения
переноса.
Семинар № 2 (14.02.14). Построение схем для
решения линейного уравнения переноса в
пространстве неопределенных коэффициентов.
Семинар № 3 (21.02.14). Понятие монотонности
разностных схем. Теорема Годунова.
Семинар № 4 (28.02.14). Обобщение на случай
системы уравнений гиперболического типа.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
2

3.

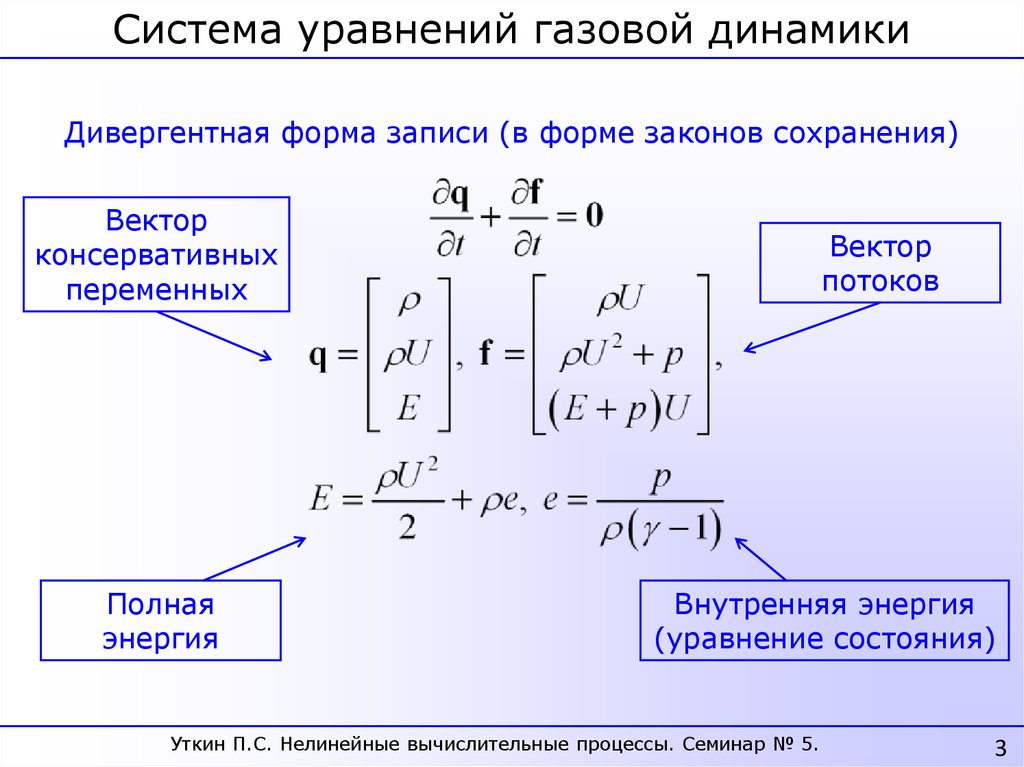
Система уравнений газовой динамики
Дивергентная форма записи (в форме законов сохранения)
Вектор
консервативных
переменных
Полная
энергия
Вектор
потоков
Внутренняя энергия
(уравнение состояния)
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
3

4.

Анализ системы уравнений газовой динамики
Характеристическая
форма
Матрица
Якоби
Скорость звука
Куликовский А.Г., Погорелов Н.В.,
Семенов А.Ю. Математические вопросы
численного решения гиперболических
систем уравнений. – М.: Физматлит, 2001.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
4

5.

Гиперболическая система уравнений
• Наличие конечной скорости распространения
бесконечно слабых возмущений
• Возможность существования разрывных решений даже
для гладких начальных данных
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
5

6.

Метод конечных объемов (1)
Для произвольной компоненты
вектора консервативных переменных:
Vm
или
(q1m , q2m , … )
z
Проинтегрируем по объему ячейки
расчетной сетки и по времени:
0
y
x
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
6

7.

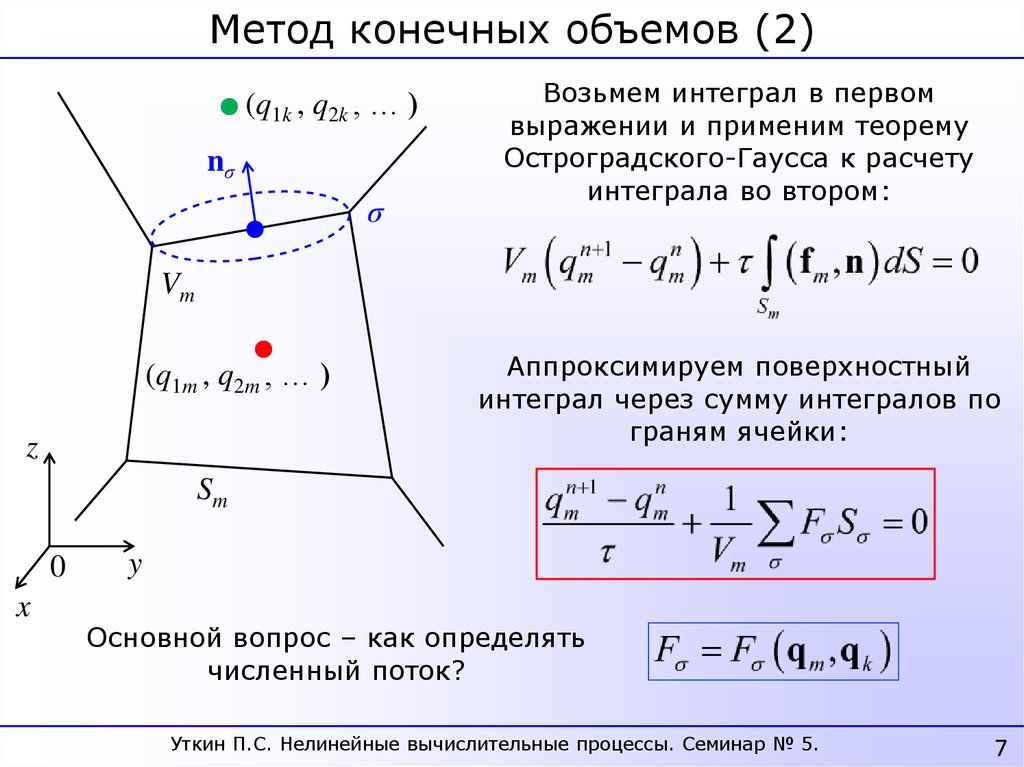
Метод конечных объемов (2)
(q1k , q2k , … )
nσ
σ
Возьмем интеграл в первом
выражении и применим теорему
Остроградского-Гаусса к расчету
интеграла во втором:
Vm
(q1m , q2m , … )
z
Аппроксимируем поверхностный
интеграл через сумму интегралов по
граням ячейки:
Sm
0
x
y
Основной вопрос – как определять
численный поток?
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
7

8.

Постановка задачи о распаде произвольного разрыва
Задача Коши для системы уравнений газовой динамики
с разрывом первого рода в начальных данных
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
8

9.

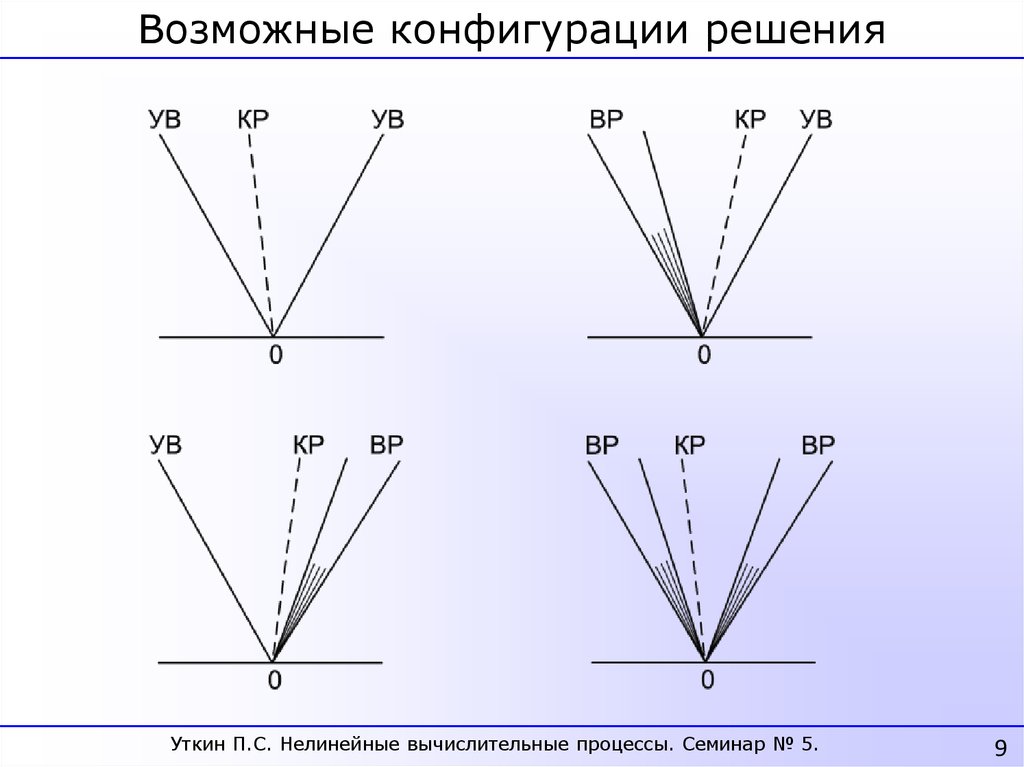
Возможные конфигурации решения
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
9

10.

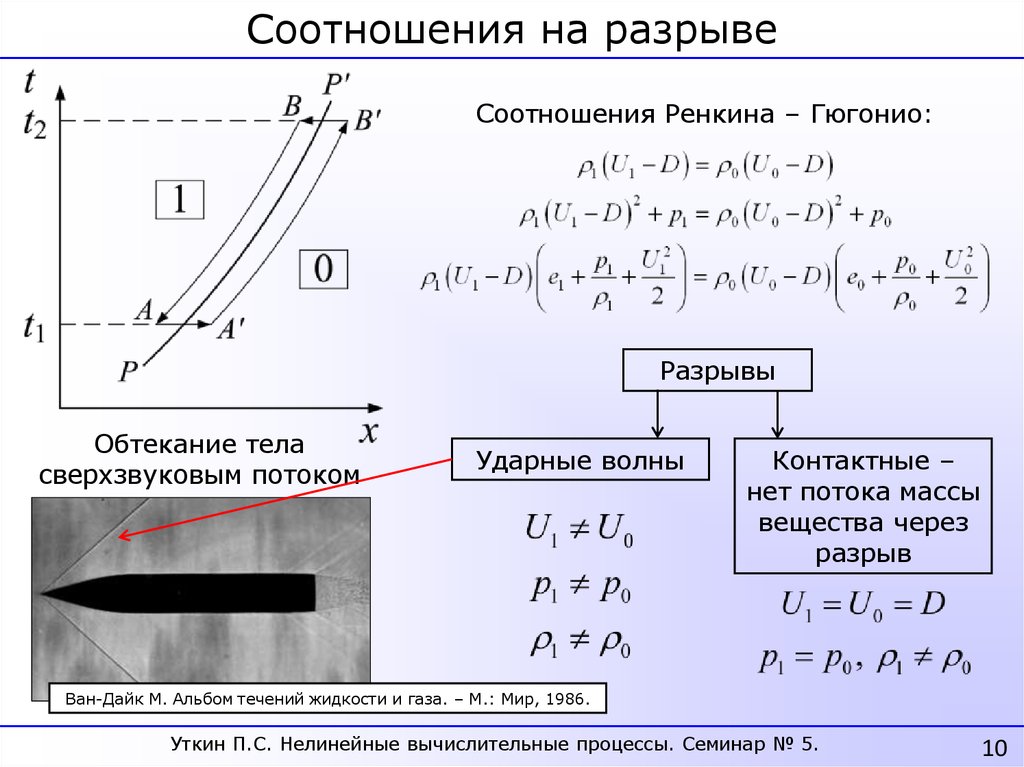
Соотношения на разрыве
Соотношения Ренкина – Гюгонио:
Разрывы
Обтекание тела
сверхзвуковым потоком
Ударные волны
Контактные –
нет потока массы
вещества через
разрыв
Ван-Дайк М. Альбом течений жидкости и газа. – М.: Мир, 1986.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
10

11.

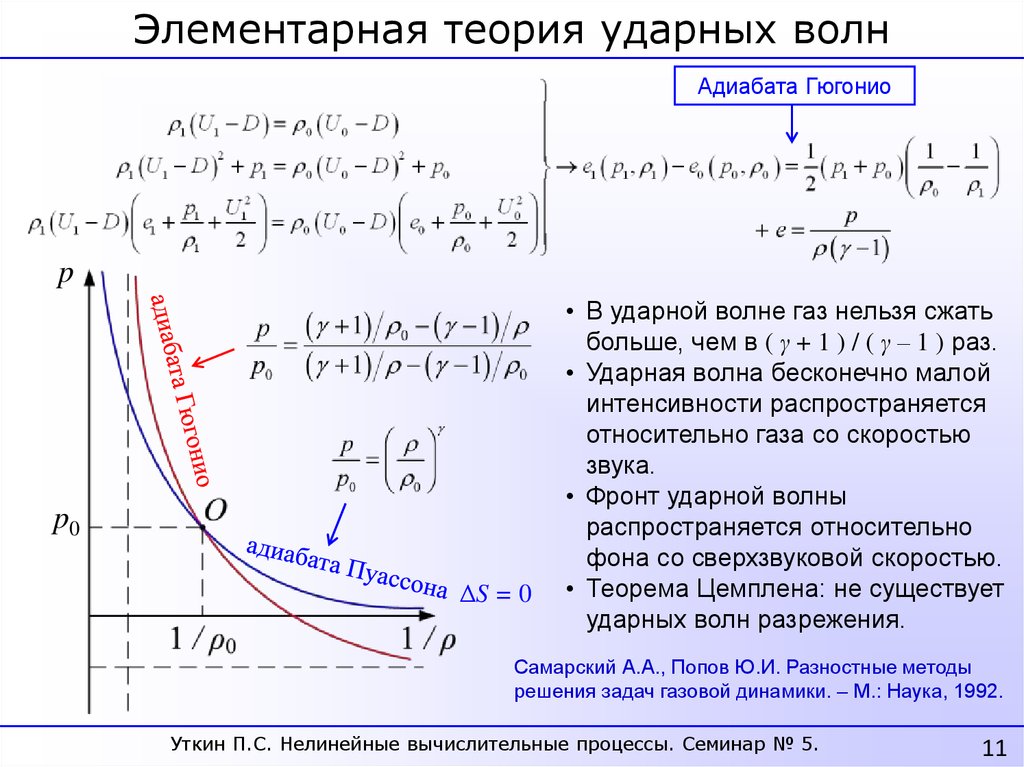
Элементарная теория ударных волн
Адиабата Гюгонио
p
p0
ΔS = 0
• В ударной волне газ нельзя сжать
больше, чем в ( γ + 1 ) / ( γ – 1 ) раз.
• Ударная волна бесконечно малой
интенсивности распространяется
относительно газа со скоростью
звука.
• Фронт ударной волны
распространяется относительно
фона со сверхзвуковой скоростью.
• Теорема Цемплена: не существует
ударных волн разрежения.
Самарский А.А., Попов Ю.И. Разностные методы
решения задач газовой динамики. – М.: Наука, 1992.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
11

12.

Соотношения для ударных волн и волн разрежения
«левая» УВ
«правая» УВ
«левая» ВР
«правая» ВР
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
12

13.

Метод Ньютона для нахождения давления на контактном разрыве
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
13

14.

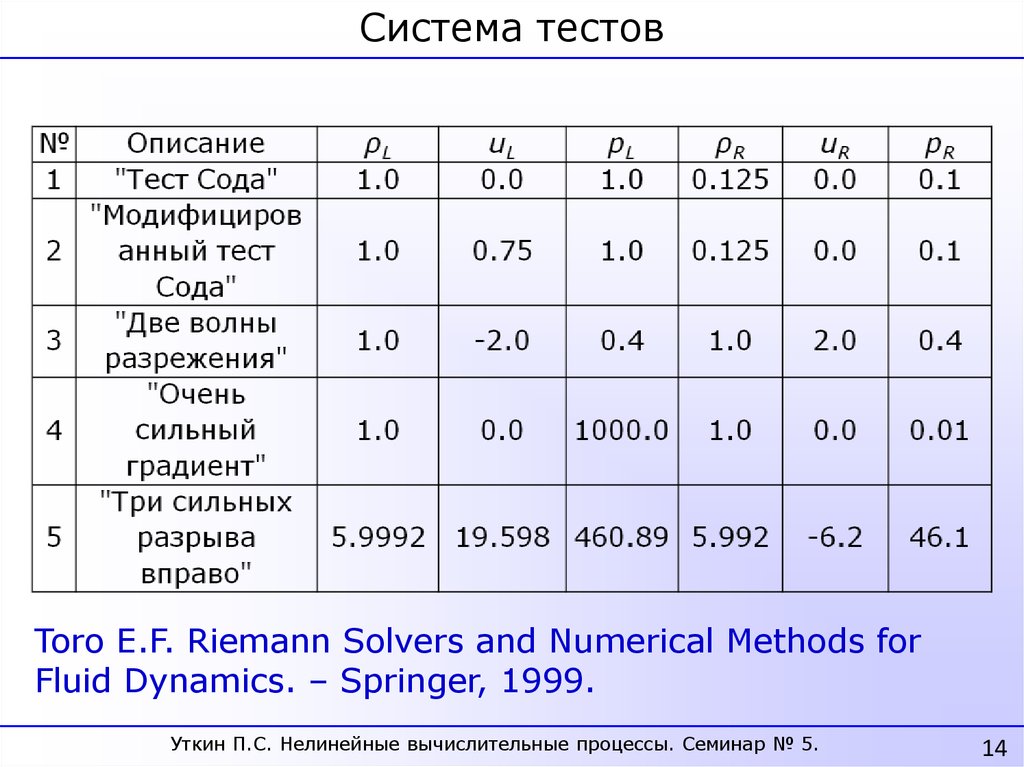
Система тестов
Toro E.F. Riemann Solvers and Numerical Methods for
Fluid Dynamics. – Springer, 1999.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
14

15.

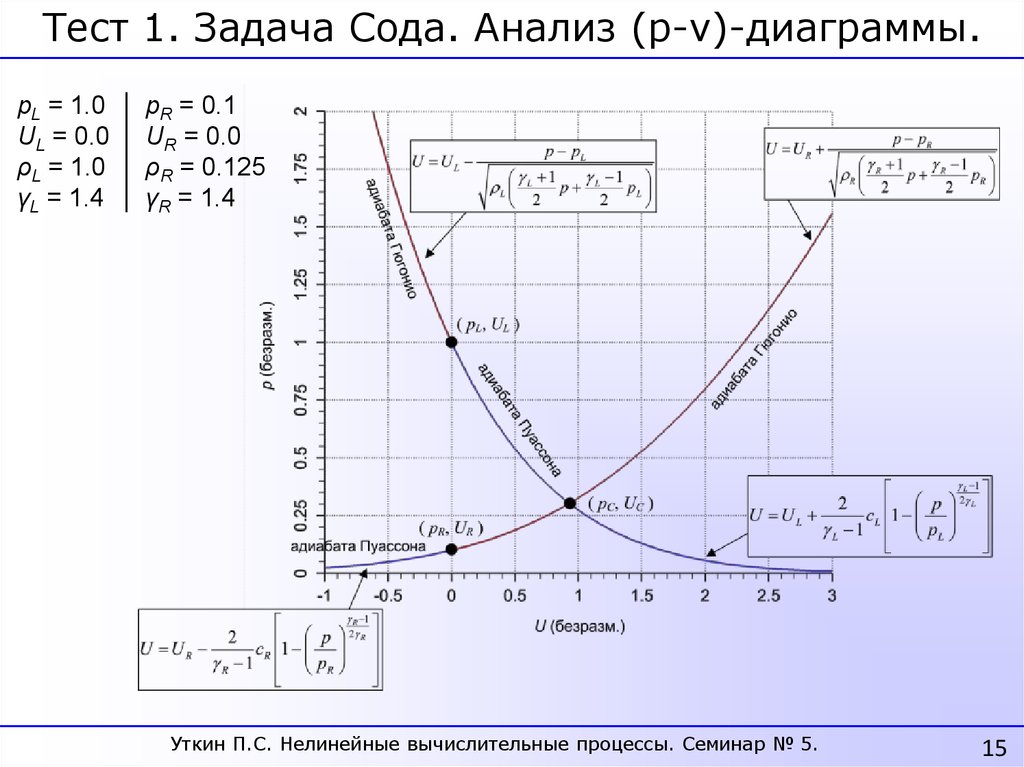
Тест 1. Задача Сода. Анализ (p-v)-диаграммы.
pL = 1.0
UL = 0.0
ρL = 1.0
γL = 1.4
pR = 0.1
UR = 0.0
ρR = 0.125
γR = 1.4
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
15

16.

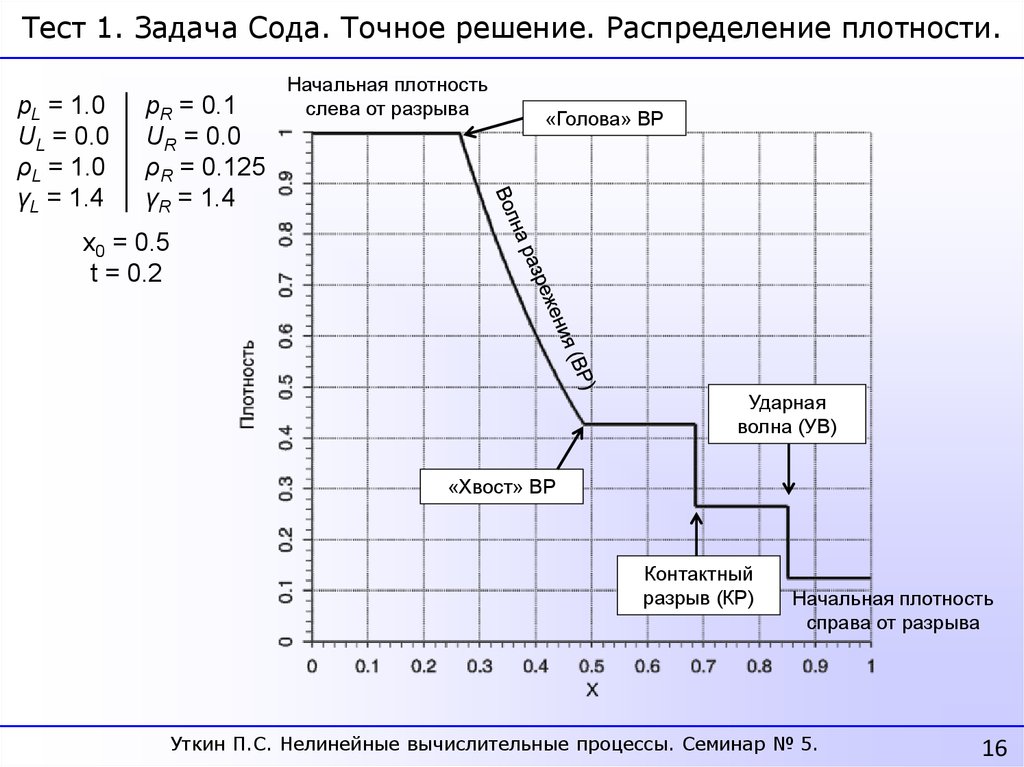
Тест 1. Задача Сода. Точное решение. Распределение плотности.
pL = 1.0
UL = 0.0
ρL = 1.0
γL = 1.4
pR = 0.1
UR = 0.0
ρR = 0.125
γR = 1.4
Начальная плотность
слева от разрыва
«Голова» ВР
x0 = 0.5
t = 0.2
Ударная
волна (УВ)
«Хвост» ВР
Контактный
разрыв (КР)
Начальная плотность
справа от разрыва
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
16

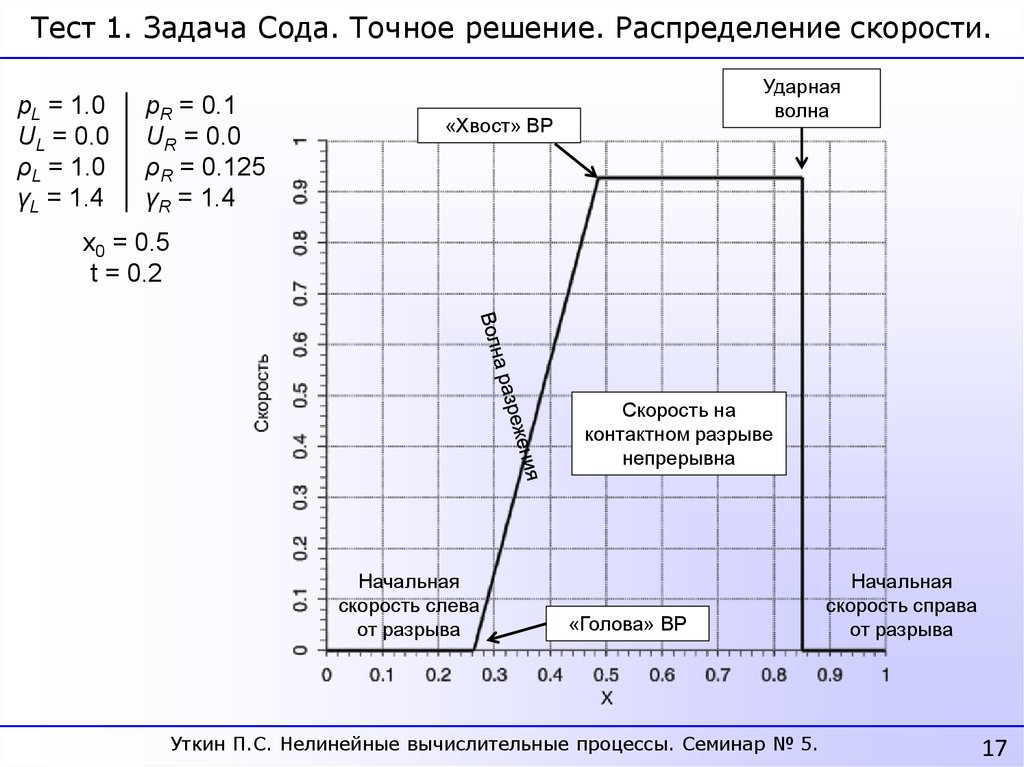
17.

Тест 1. Задача Сода. Точное решение. Распределение скорости.
pL = 1.0
UL = 0.0
ρL = 1.0
γL = 1.4
pR = 0.1
UR = 0.0
ρR = 0.125
γR = 1.4
Ударная
волна
«Хвост» ВР
x0 = 0.5
t = 0.2
Скорость на
контактном разрыве
непрерывна
Начальная
скорость слева
от разрыва
«Голова» ВР
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
Начальная
скорость справа
от разрыва
17

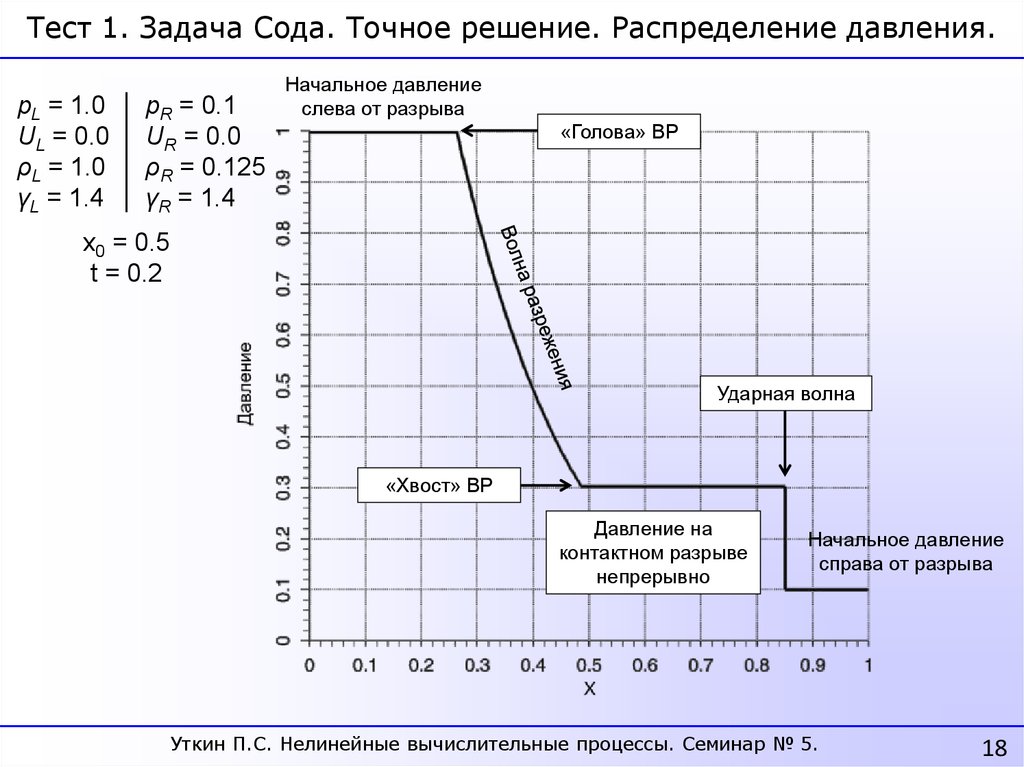
18.

Тест 1. Задача Сода. Точное решение. Распределение давления.
pL = 1.0
UL = 0.0
ρL = 1.0
γL = 1.4
pR = 0.1
UR = 0.0
ρR = 0.125
γR = 1.4
Начальное давление
слева от разрыва
«Голова» ВР
x0 = 0.5
t = 0.2
Ударная волна
«Хвост» ВР
Давление на
контактном разрыве
непрерывно
Начальное давление
справа от разрыва
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
18

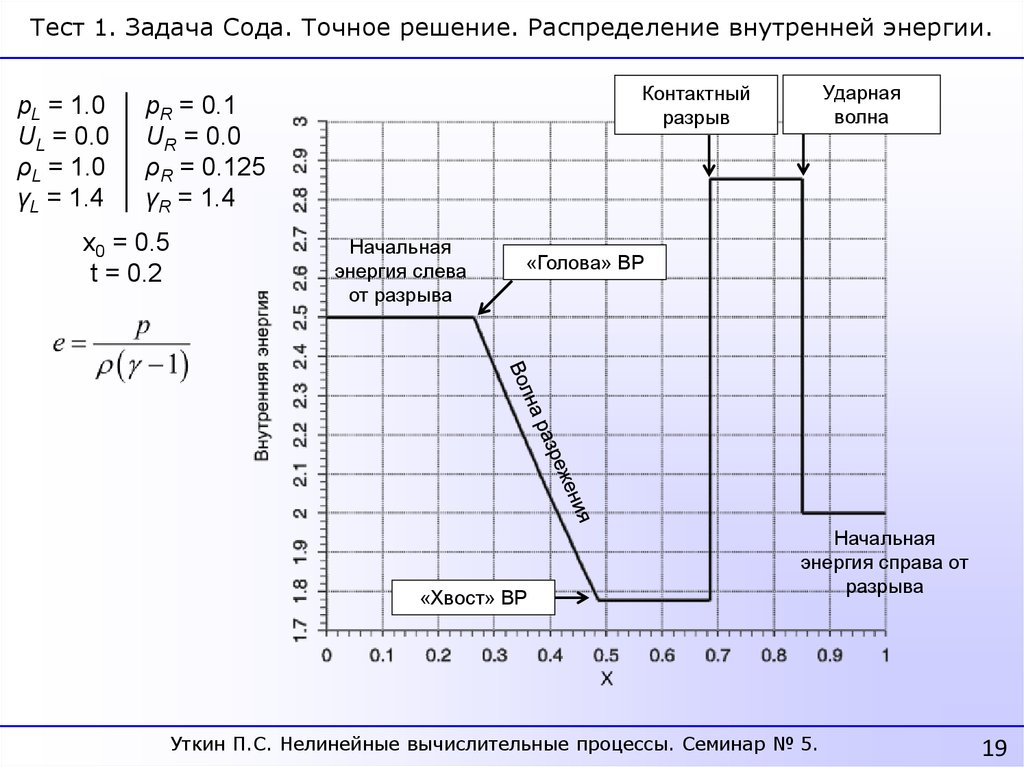
19.

Тест 1. Задача Сода. Точное решение. Распределение внутренней энергии.
pL = 1.0
UL = 0.0
ρL = 1.0
γL = 1.4
x0 = 0.5
t = 0.2
Ударная
волна
Контактный
разрыв
pR = 0.1
UR = 0.0
ρR = 0.125
γR = 1.4
Начальная
энергия слева
от разрыва
«Голова» ВР
«Хвост» ВР
Начальная
энергия справа от
разрыва
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
19

20.

Алгоритм построения точного решения
1. Определяем по (p-v)-диаграмме
конфигурацию, возникающую при распаде.
Самарский А.А., Попов Ю.П. Разностные методы
решения задач газовой динамики. – М.: Наука, 1992.
2. В результате решения нелинейного
алгебраического уравнения методом Ньютона
ищем давление на контактном разрыве.
3. Определяем оставшиеся параметры –
скорости ударных волн и наклоны крайних
характеристик, описывающих веер волны
разрежения.
Годунов С.К. и др. Численное решение многомерных
задач газовой динамики. – М.: Наука, 1976.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
20

21.

Сергей
Константинович
Годунов
род. 1929 г.,
академик РАН
Тестирование схемы
С.К. Годунова решения
уравнений газовой
динамики
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
21

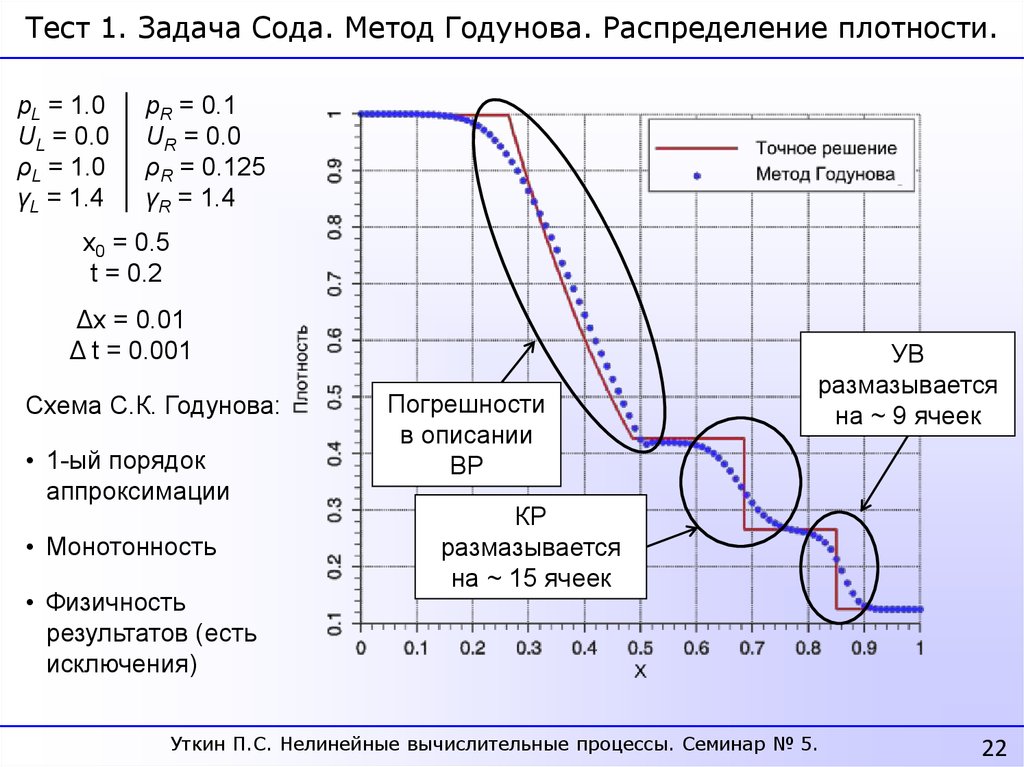
22.

Тест 1. Задача Сода. Метод Годунова. Распределение плотности.
pL = 1.0
UL = 0.0
ρL = 1.0
γL = 1.4
pR = 0.1
UR = 0.0
ρR = 0.125
γR = 1.4
x0 = 0.5
t = 0.2
Δx = 0.01
Δ t = 0.001
Схема С.К. Годунова:
• 1-ый порядок
аппроксимации
• Монотонность
• Физичность
результатов (есть
исключения)
Погрешности
в описании
ВР
УВ
размазывается
на ~ 9 ячеек
КР
размазывается
на ~ 15 ячеек
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
22

23.

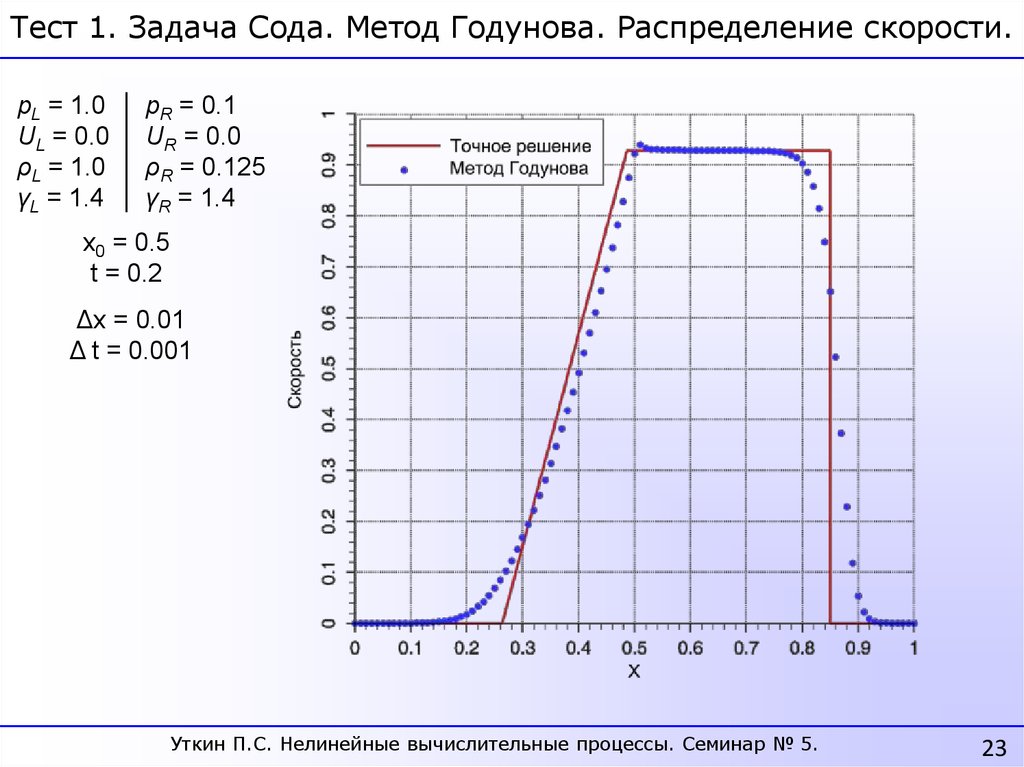
Тест 1. Задача Сода. Метод Годунова. Распределение скорости.
pL = 1.0
UL = 0.0
ρL = 1.0
γL = 1.4
pR = 0.1
UR = 0.0
ρR = 0.125
γR = 1.4
x0 = 0.5
t = 0.2
Δx = 0.01
Δ t = 0.001
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
23

24.

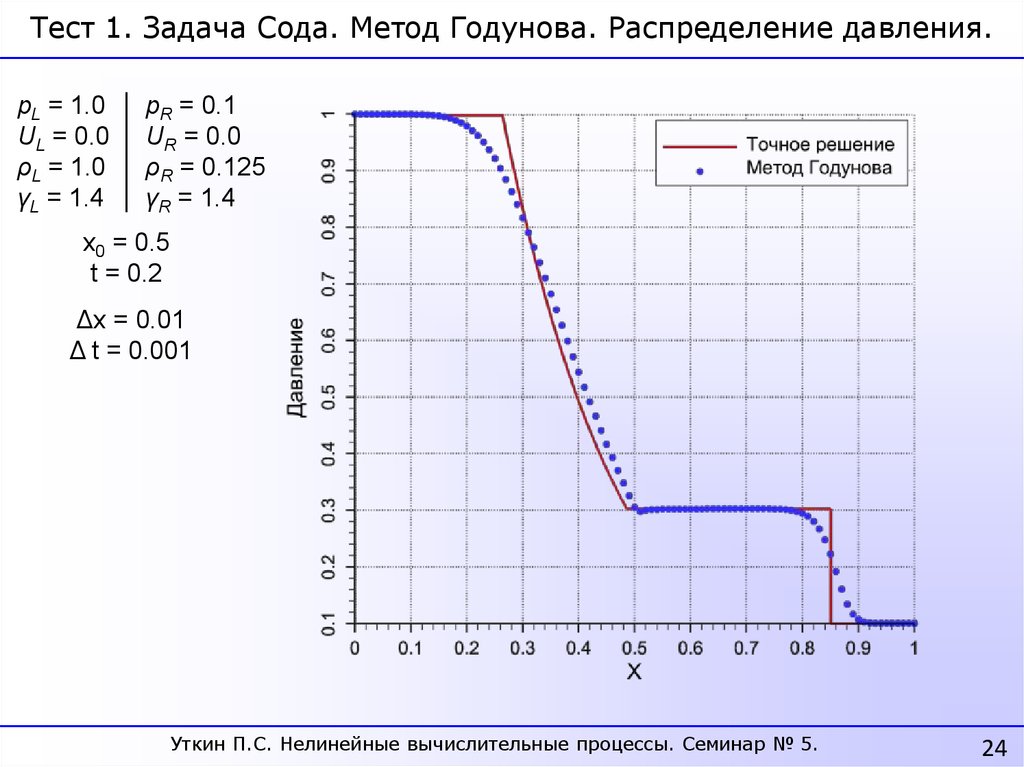
Тест 1. Задача Сода. Метод Годунова. Распределение давления.
pL = 1.0
UL = 0.0
ρL = 1.0
γL = 1.4
pR = 0.1
UR = 0.0
ρR = 0.125
γR = 1.4
x0 = 0.5
t = 0.2
Δx = 0.01
Δ t = 0.001
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
24

25.

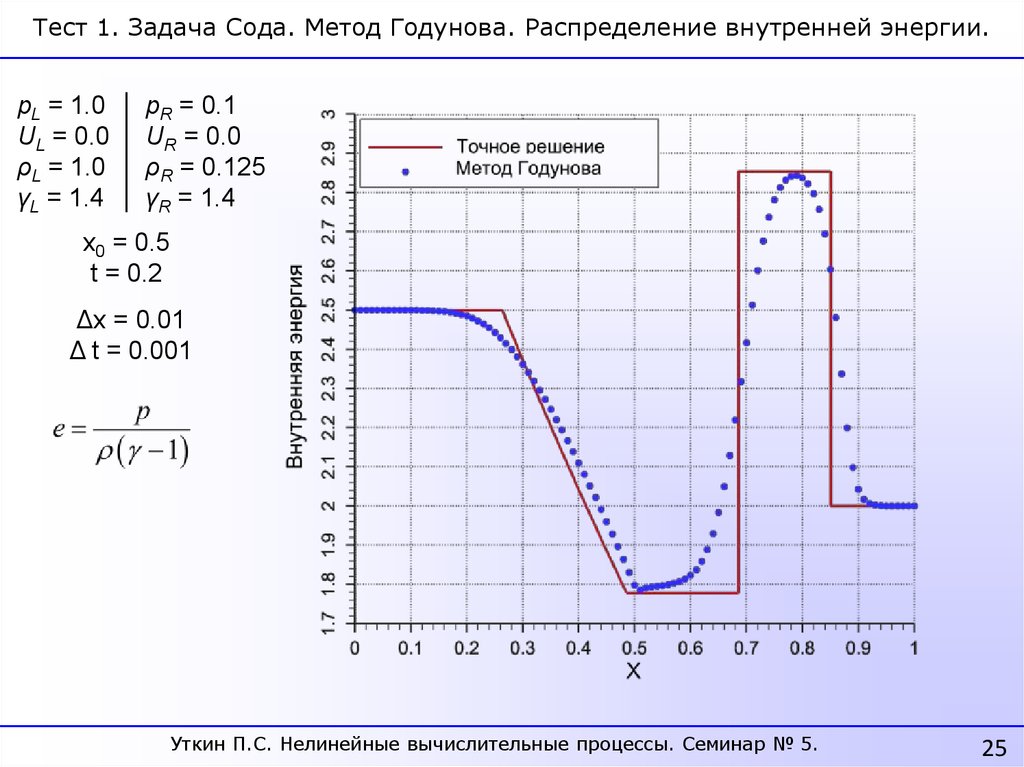
Тест 1. Задача Сода. Метод Годунова. Распределение внутренней энергии.
pL = 1.0
UL = 0.0
ρL = 1.0
γL = 1.4
pR = 0.1
UR = 0.0
ρR = 0.125
γR = 1.4
x0 = 0.5
t = 0.2
Δx = 0.01
Δ t = 0.001
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
25

26.

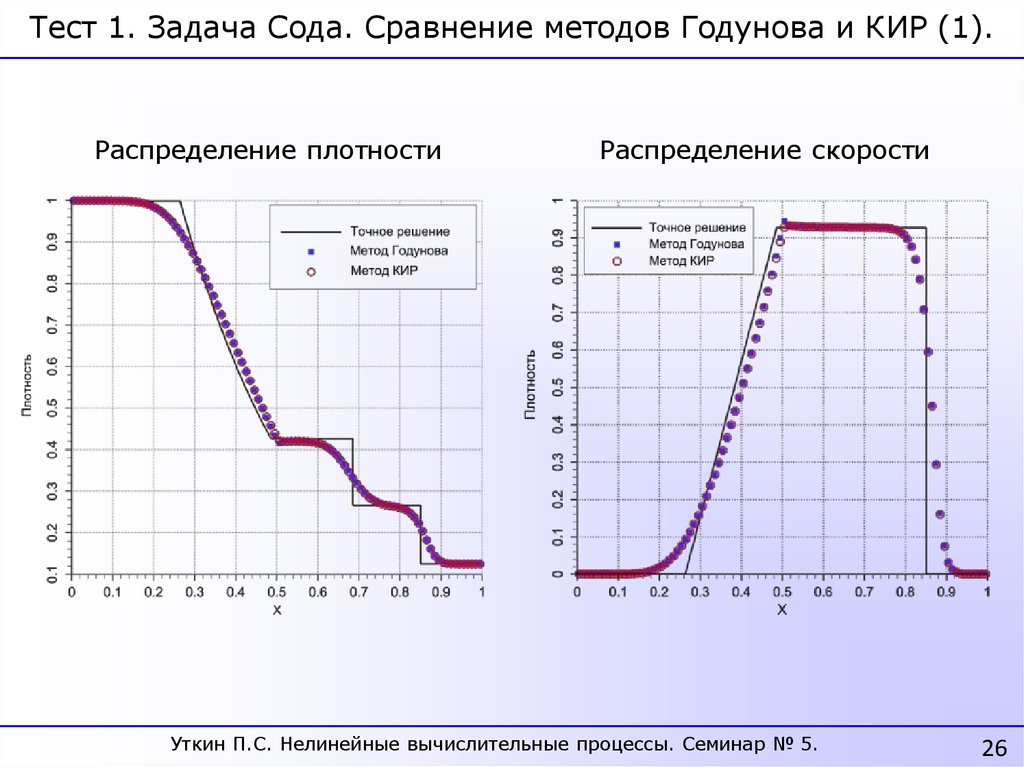
Тест 1. Задача Сода. Сравнение методов Годунова и КИР (1).
Распределение плотности
Распределение скорости
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
26

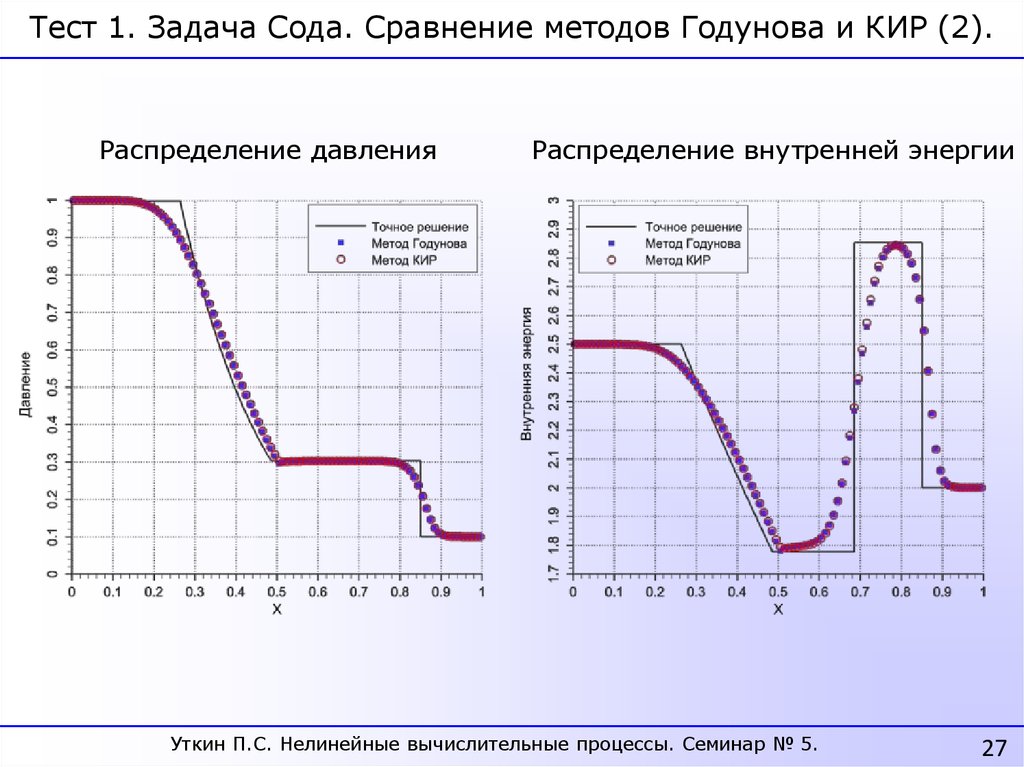
27.

Тест 1. Задача Сода. Сравнение методов Годунова и КИР (2).
Распределение давления
Распределение внутренней энергии
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
27

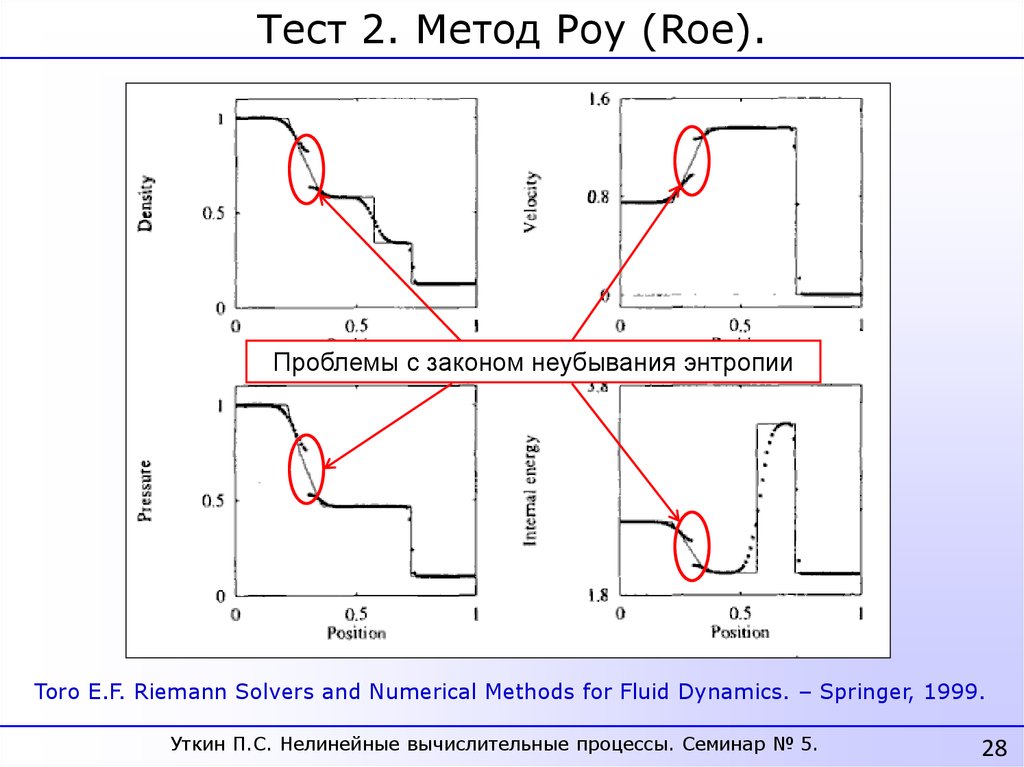
28.

Тест 2. Метод Роу (Roe).
Проблемы с законом неубывания энтропии
Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. – Springer, 1999.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
28

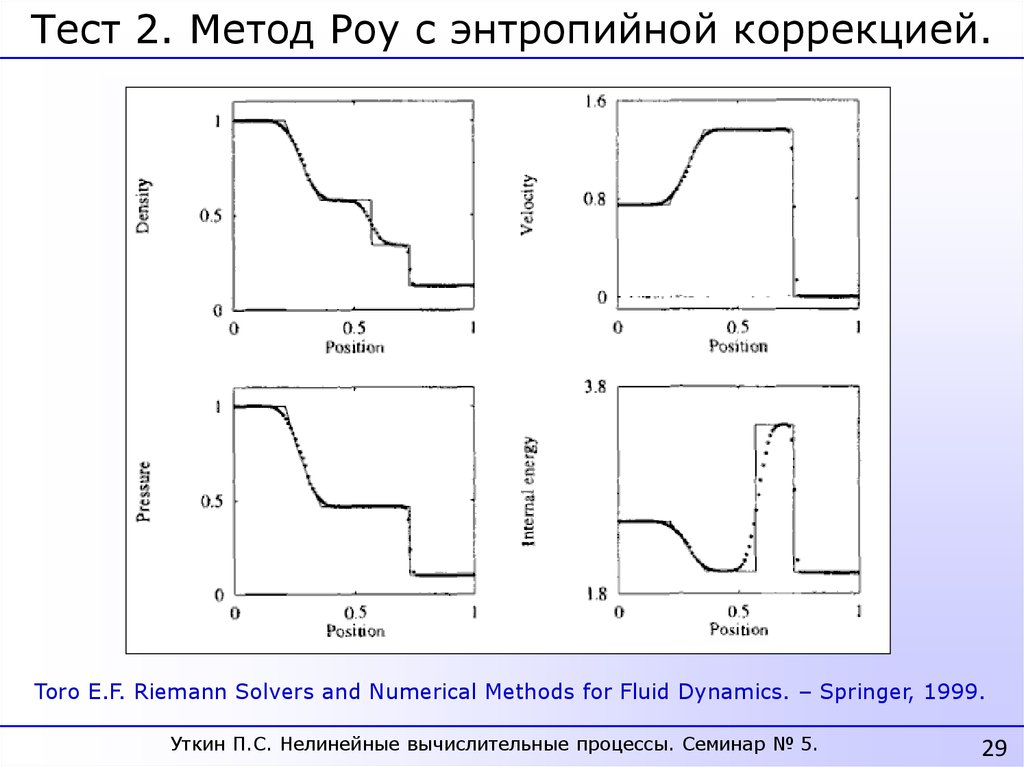
29.

Тест 2. Метод Роу с энтропийной коррекцией.
Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. – Springer, 1999.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
29

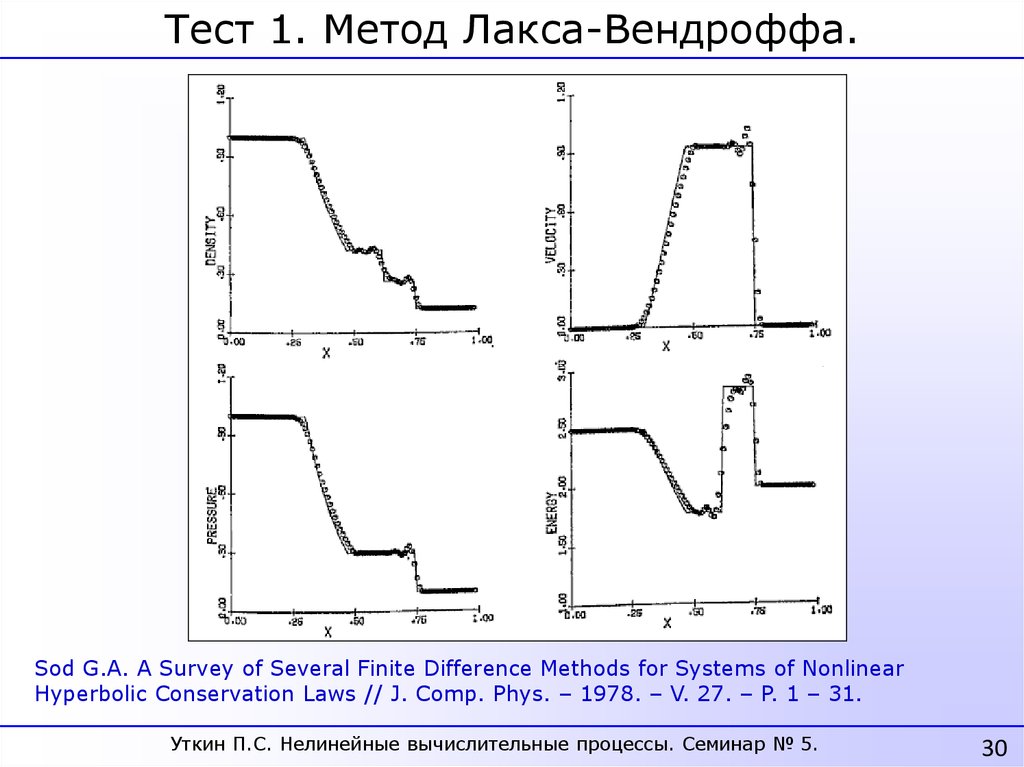
30.

Тест 1. Метод Лакса-Вендроффа.
Sod G.A. A Survey of Several Finite Difference Methods for Systems of Nonlinear
Hyperbolic Conservation Laws // J. Comp. Phys. – 1978. – V. 27. – P. 1 – 31.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
30

31.

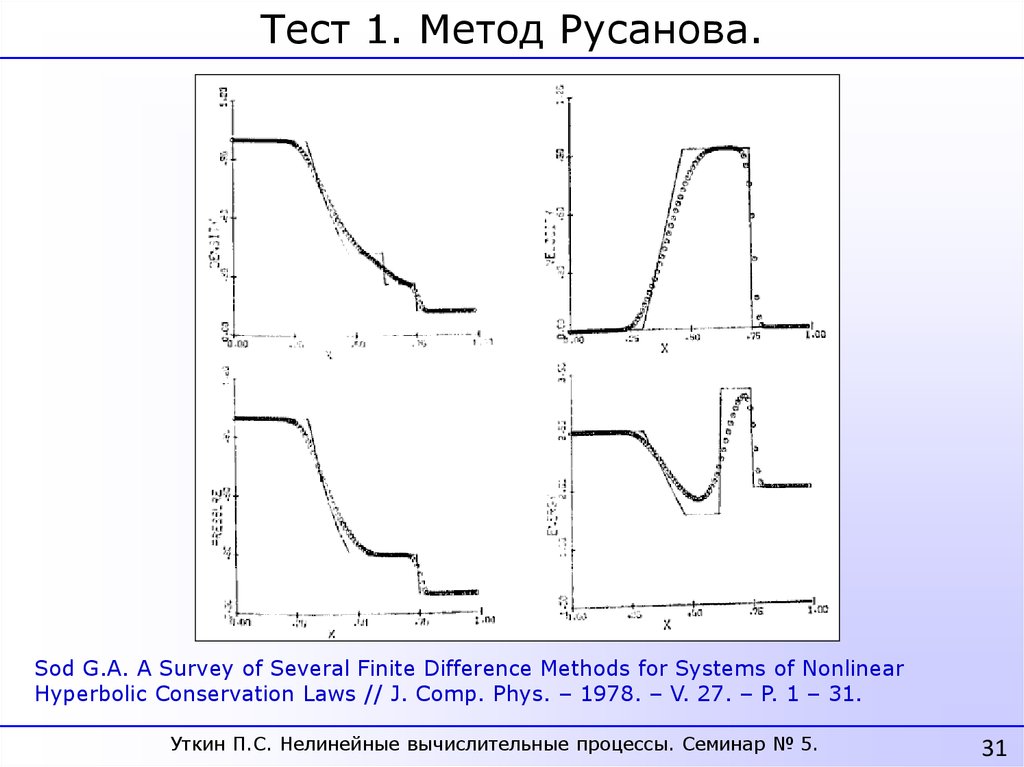
Тест 1. Метод Русанова.
Sod G.A. A Survey of Several Finite Difference Methods for Systems of Nonlinear
Hyperbolic Conservation Laws // J. Comp. Phys. – 1978. – V. 27. – P. 1 – 31.
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
31

32.

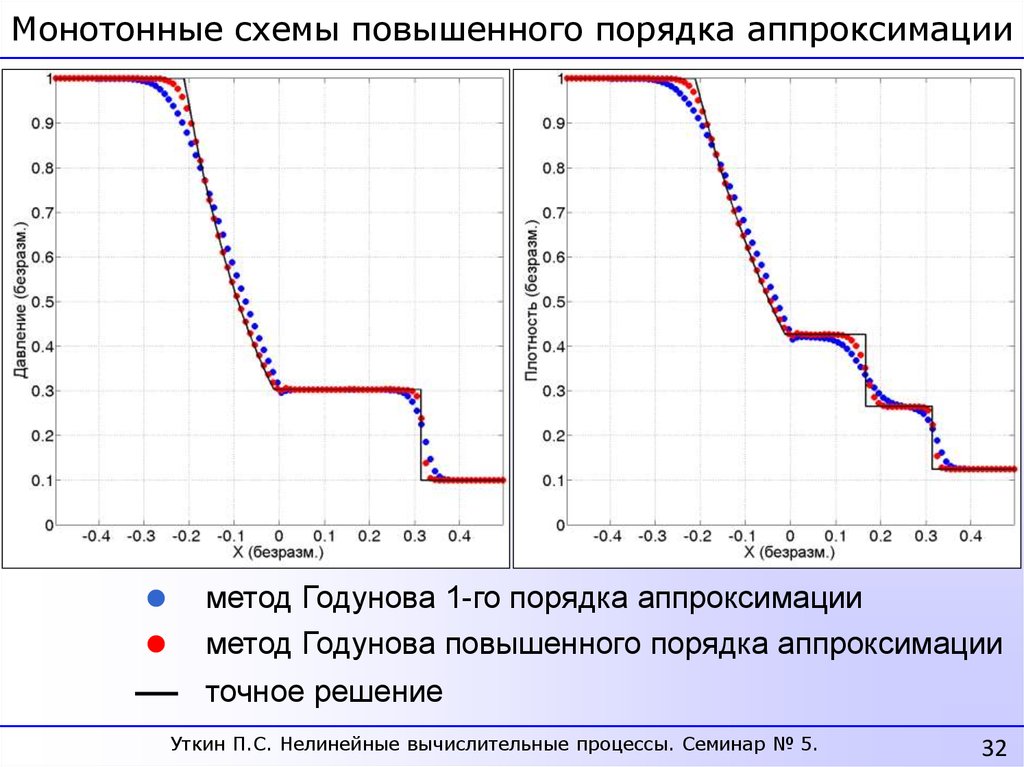
Монотонные схемы повышенного порядка аппроксимации
метод Годунова 1-го порядка аппроксимации
метод Годунова повышенного порядка аппроксимации
точное решение
Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
32