Похожие презентации:
Быстрые переключения нелинейных систем
1.
Институт ФизикиМикроструктур РАН
Центр криогенной наноэлектроники
Нижегородский государственный
технический университет им. Р.Е. Алексеева
Быстрые переключения
нелинейных систем
Панкратов А.Л.
1
2. Джозефсоновские контакты
Is= Ic sin(φ)2
2
2 ( x) sin( )
2
t
t x
2
3. Джозефсоновские контакты
34. Криостаты ЦКН НГТУ
45. Компактные криостаты
56.
The Unique Cryogen-freeRefrigerator of Oxford
Instruments for 10 mK!
(first in Russia )
Started at NSTU in June 2011!
(the first IV curve on June 17, 2011)
66
6
7.
Disadvantage of current technologiesThe focal plane of Planck experiment
The focal plane of COrE experiment
7
7
8.
Cold-Electron Bolometer (CEB) with Capacitive Coupling to the AntennaMain features of the CEB:
1. High sensitivity due to electron cooling effect:
2. High dynamic range due to direct electron cooling
3. Very easy to fabricate in arrays on planar substrate
4. Insensitivity to Cosmic Rays
5. Resonance Cold-Electron Bolometer (RCEB) for MultiFrequency Pixels
9.
Cosmic Rays- dramatic problem!Cosmic Ray tests of CEB in Rome:
- 137Cs source (660 keV photons) in front of
the window.
J. Low Temp. Phys., 176, 3-4 323, 2014
Planck HF Insrument
- No single glitch was detected!
Expectation time for
a single glitch – 40 hours!
Double protection against Cosmic Rays
by extremely small volume of absorber!
Spider-web with TES for LSPE
CEB for LSPE
Array of 6 CEBs
2
S=10mm
80 nm
Te (T
5
ph
P 1/5 Absorber
)
ΣV
Gain
in Area
:1000
Filling factor- 5%
S=5mm2
h=10 nm in thickness
:100
in volume
:105
h=2 mm 10 mm
9
10.
The position of slots, chess orderThe microstrip-fed slot antennas.
At the edge of each microstrip line waveguide port is located.
10
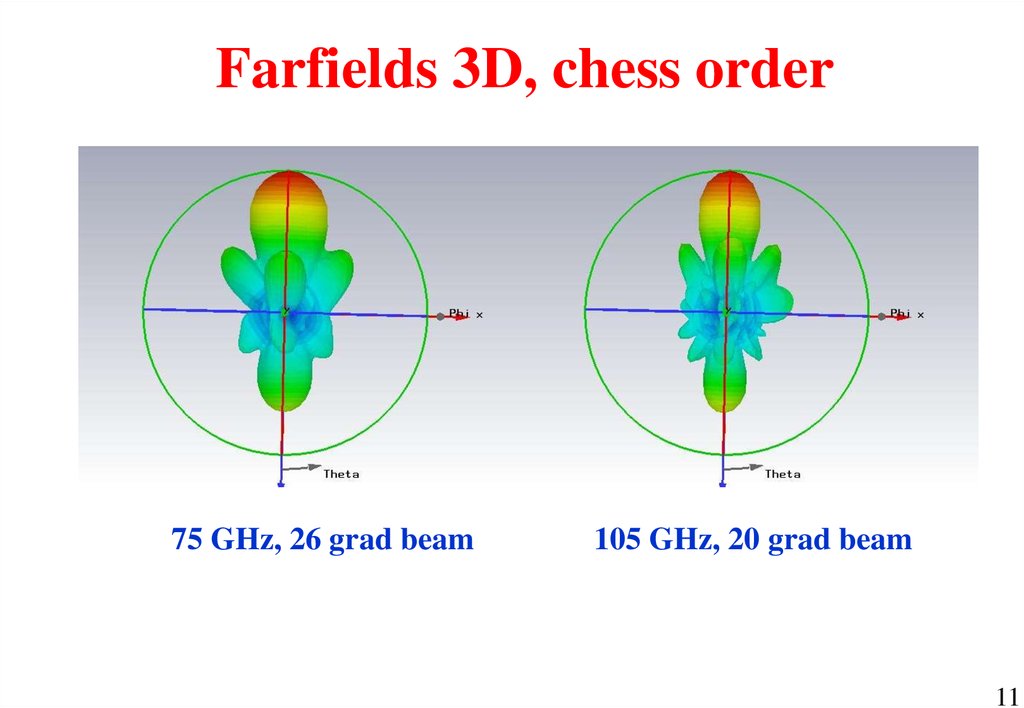
11.
Farfields 3D, chess order75 GHz, 26 grad beam
105 GHz, 20 grad beam
11
12.
Иерархия шумовТехнические шумы (узкополосные)
Естественные шумы (широкополосные):
Тепловой шум SI(w)~kT/R
Дробовой шум SI(w)~eI/2
Квантовый шум SI(w)~hw/R
Oelsner G., Revin L.S., Ilichev E., Pankratov A.L., Meyer H.-G., Gronberg L., Hassel J., and Kuzmin L.S., Appl. Phys. Lett., 103, 142605 (2013).
12
13.
Что мы понимаем под переключением?10.0
u( )
5.0
0.0
-5.0
-10.0
-10.0
-6.0
-2.0
2.0
6.0
10.0
13
14.
Что мы понимаем под минимизацией шумов?10.0
u( )
5.0
~e
0.0
U / kT
-5.0
~ kT
-10.0
-10.0
-6.0
-2.0
2.0
6.0
10.0
14
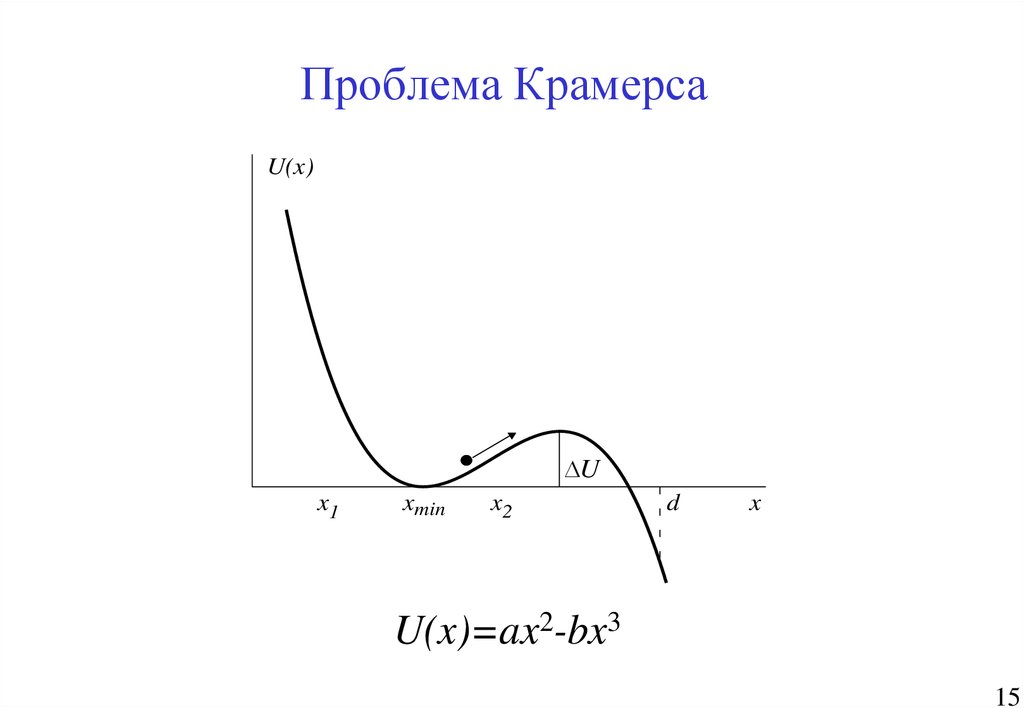
15. Проблема Крамерса
U(x)U
x1
xmin
x2
d
x
U(x)=ax2-bx3
15
16. Уравнения Ланжевена и Фоккера-Планка
dx(t )1 dU ( x)
(t )
dt
h dx
< (t)>=0, < (t) (t+ )>=D ( ), D=2kT/h
W ( x, t )
G( x, t ) 1 du ( x)
W ( x, t )
W ( x, t )
t
x
B x dx
x
B=1/D, u(x)=U(x)/kT, W(c,t)=0, G(d,t)=0.
16
17.
Безразмерное уравнение ФПW ( x, t )
du ( x)
D
W ( x, t )
W ( x, t )
t
x dx
x
Замена функции:
W ( x, t ) ( x, t )e
Замена времени:
u ( x)
2
t i
Безразмерное уравнение Шредингера
2 ( x, )
( x, )
iD
V ( x) ( x, )
2
x
Связь потенциалов в уравнении ФП и Шредингера
1 d 2u ( x) 1 du ( x)
V ( x)
2
2 dx
2 dx
2
17
18.
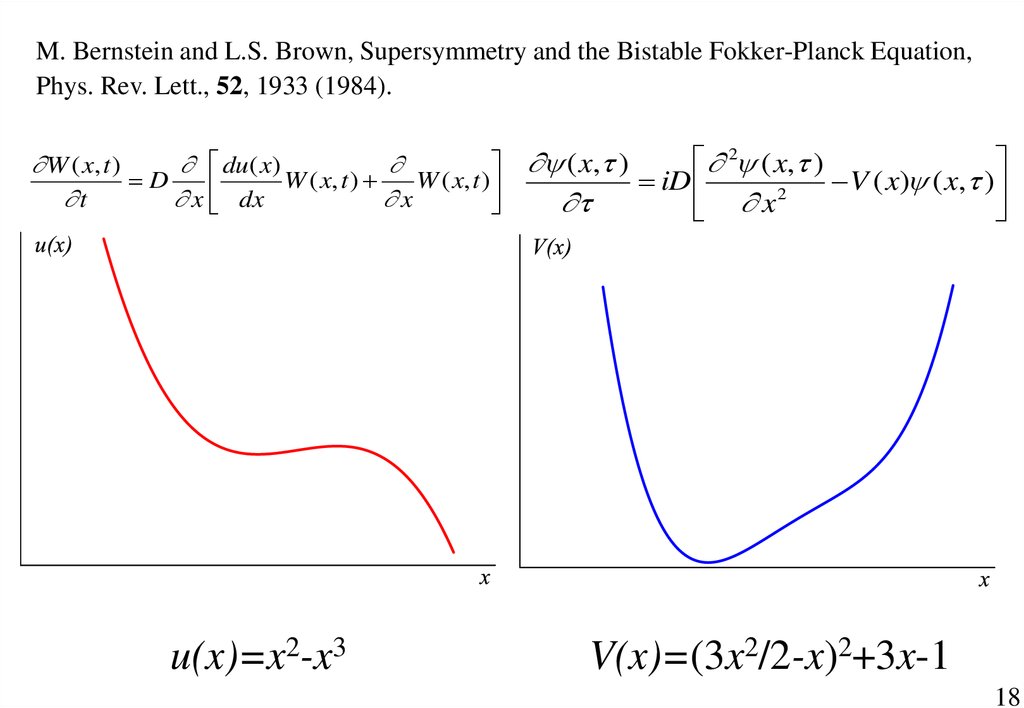
M. Bernstein and L.S. Brown, Supersymmetry and the Bistable Fokker-Planck Equation,Phys. Rev. Lett., 52, 1933 (1984).
2 ( x, )
( x, )
W ( x, t )
du ( x)
D
W ( x, t )
W ( x, t )
iD
V ( x) ( x, )
2
t
x dx
x
x
u(x)=x2-x3
V(x)=(3x2/2-x)2+3x-1
18
19. Временные характеристики
1. Моменты времени первого достижения границ(Понтрягин, Андронов, Витт, ЖЭТФ, 1933 г.)
2. Метод Крамерса: ~exp( U/kT), Physica, 1940 г.
3. Эффективное собственное число (Рискен, Юнг, Гаранин)
4. Обобщенное моментное разложение (Надлер, Шультен)
5. Интегральное время релаксации и цепные дроби
(Коффей, Калмыков, Титов)
[ P(t ) P( )]dt
0
P ( 0) P ( )
d
P(t ) W ( x, t )dt
t n t n w(t )dt
0
вероятность нахождения
в области (c,d)
c
19
20.
U(x)U(x)
U
x1
xmin
x2
U
d
x
x1
xmin
x2
d
x
U(x)
x
20
21. Метод преобразования Лапласа
d 2Y ( x, s) d du( x)Y ( x, s) sBY ( x, s) B ( x x0 )
2
dx
dx dx
Y ( x, s) W ( x, t )e dt
st
0
[ P(t ) P( )]dt
0
P ( 0) P ( )
G( x, s) G( x, t )e st dt
0
sPˆ ( s) P( )
lim
s 0 s[ P (0) P ( )]
sPˆ ( s) P( ) G (c, s) G (d , s)
21
22.
H ( x, s) sG ( x, s) H 0 ( x) sH 1 ( x) s H 2 ( x) ...2
1 (c, x0 , d ) ( H 2 (d ) H 2 (c));
2 (c, x0 , d ) 2( H 3 (d ) H 3 (c));
n (c, x0 , d ) ( 1) n!( H n 1 (d ) H n 1 (c)).
n
d
x
d
u ( x ) u ( y )
u ( y )
u ( x)
1 B e e
dydx e
dy e dx
c
c
d
x0
2
2
exp( u ), u 1
2 2 1 F , 1
2
wc 1 i
A.N. Malakhov, A.L. Pankratov, Physica C 269, 46-54 (1996).
A.N. Malakhov, Chaos 7, 488 (1997).
A.L. Pankratov, Physics Letters A 234, 329-335 (1997).
A.L. Pankratov, B. Spagnolo, Physical Review Letters 93, 177001 (2004).
A.N. Malakhov, A.L. Pankratov, Adv. Chem. Phys. 121, 357-438 (2002).
22
23. Временная эволюция средних
n n!n
1
F (t ) F0 exp( t / )
S(w)
1
P(t)
1
0.1
u=0.14
0.1
0.01
u=4
0.01
u=2.4
u=1.4
0.001
0.001
u=1.2
0.0001
0.0001
u=7
0.00001
0.00001
0
200
400
600
800
1000
t
0
20
40
60
80
100
w
23
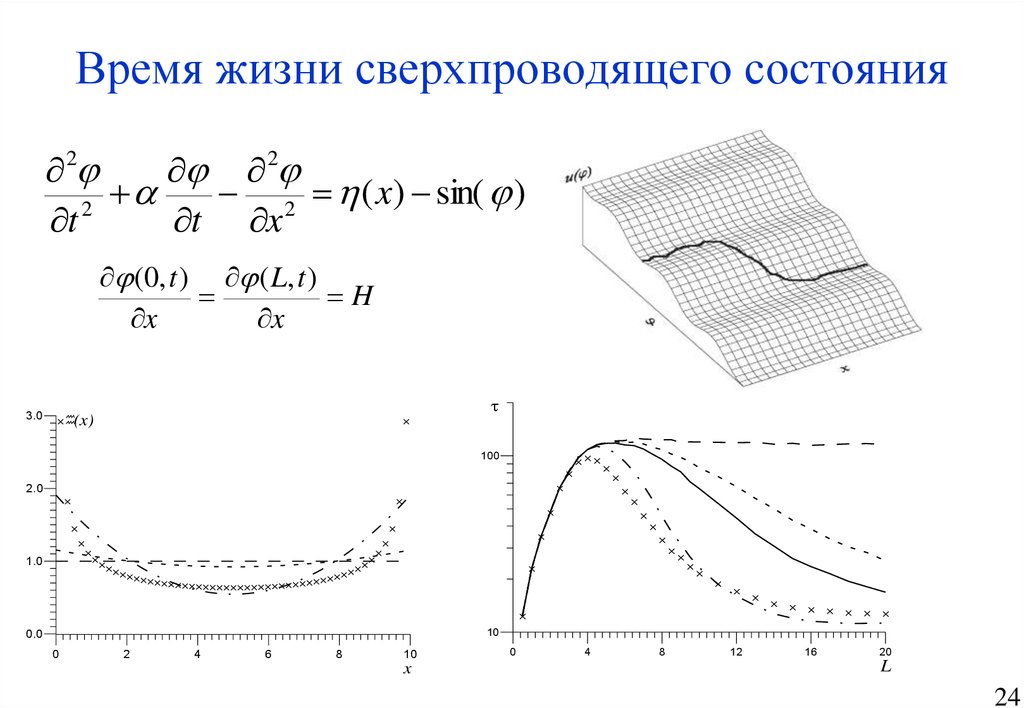
24. Время жизни сверхпроводящего состояния
22
2 ( x) sin( )
2
t
t x
(0, t ) ( L, t )
H
x
x
(x)
3.0
100
2.0
1.0
10
0.0
0
2
4
6
8
10
x
0
4
8
12
16
20
L
24
25.
K.G. Fedorov, and A.L. Pankratov, Phys. Rev. Lett., 103, 260601 (2009).25
26.
M. Buttiker, and R. Landauer, Phys. Rev. A, 23, 1397 (1981).M. Buttiker, and T. Christen, Phys. Rev. Lett. 75, 1895 (1995).
26
27.
Резонансная активацияm d 2 x(t ) dx(t )
1 dU ( x)
Asin( wt ) (t )
2
h dt
dt
h dx
P. Jung, Physics Reports 234, 175-295 (1993).
27
28. Резонансная активация?
dx(t )1 dU ( x)
Asin( wt ) (t )
dt
h dx
25
w
20
< w >ph
A=0.1
20
15
A=0.3
15
10
u*=2.4
10
u*=24
A=1
u*=12
5
5
0
0
0.1
1
10
100
0
1
10
w
100
w
A.L. Pankratov, M. Salerno, Physics Letters A 273, 162-166 (2000).
28
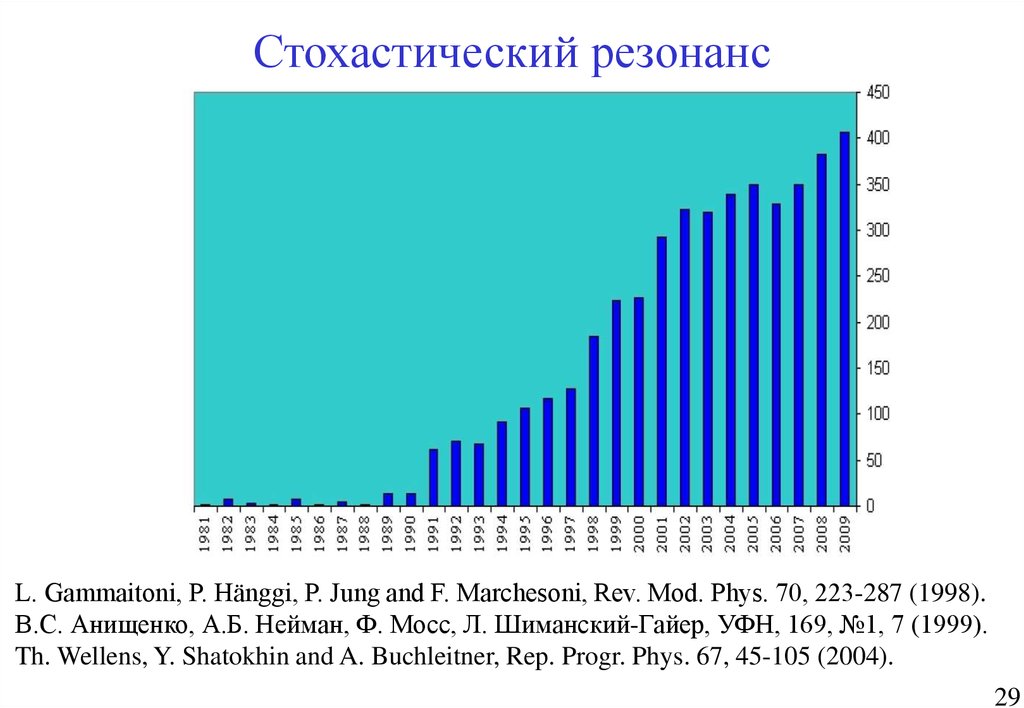
29.
Стохастический резонансL. Gammaitoni, P. Hänggi, P. Jung and F. Marchesoni, Rev. Mod. Phys. 70, 223-287 (1998).
В.С. Анищенко, А.Б. Нейман, Ф. Мосс, Л. Шиманский-Гайер, УФН, 169, №1, 7 (1999).
Th. Wellens, Y. Shatokhin and A. Buchleitner, Rep. Progr. Phys. 67, 45-105 (2004).
29
30.
Стохастический резонансdx(t )
1 dU ( x)
Asin( wt ) (t )
dt
h dx
30
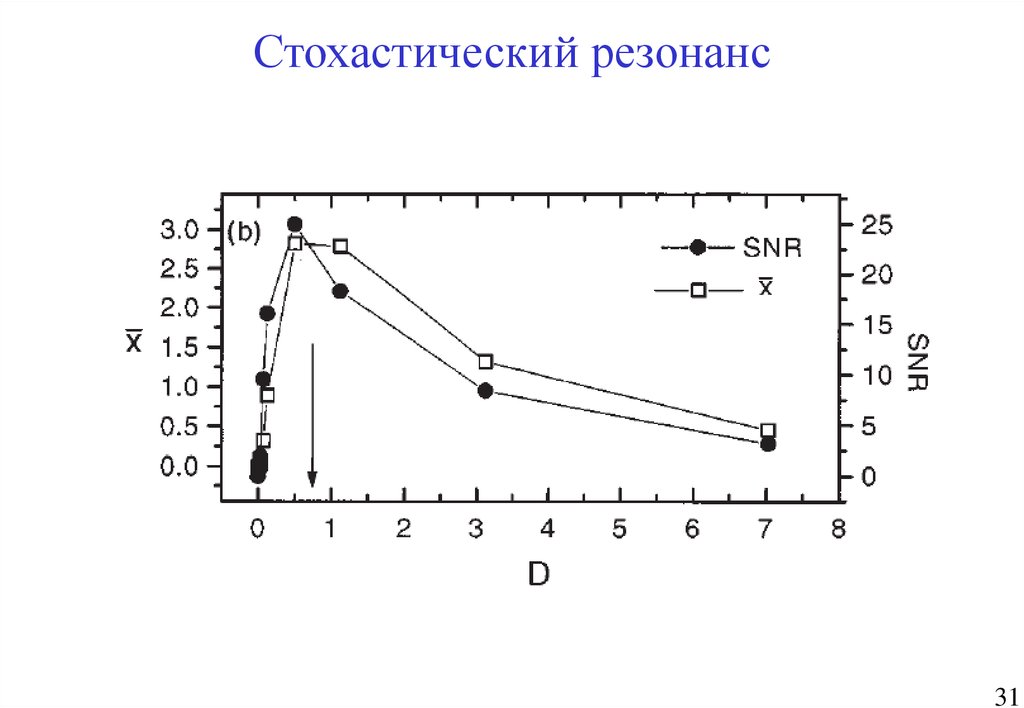
31.
Стохастический резонанс31
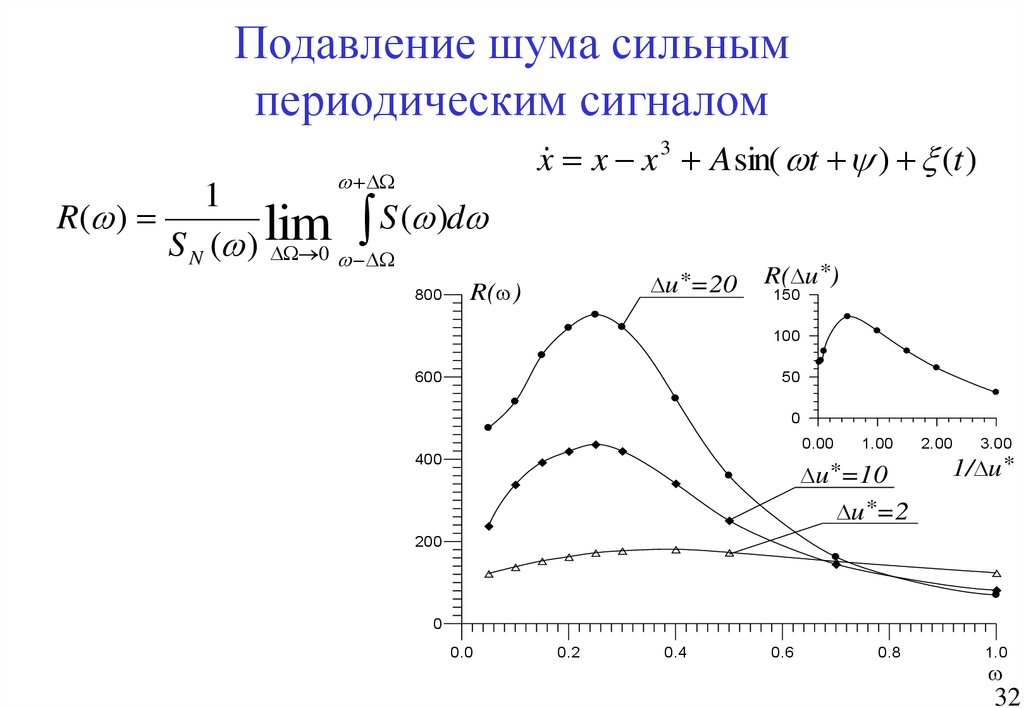
32. Подавление шума сильным периодическим сигналом
x x x 3 A sin( wt ) (t )w
1
R(w )
S (w )dw
lim
S N (w ) 0 w
800
u*=20
R(w)
R( u*)
150
100
600
50
0
0.00
400
1.00
u*=10
2.00
3.00
1/ u*
u*=2
200
0
0.0
0.2
0.4
0.6
0.8
1.0
w
32
33. Подавление ошибок переключения в устройствах БОК логики
dsin( ) i (t ) iF (t )
dt
t tw(t )dt ,
t t
2
2
0
y d
i tan( y / 2) 1
1 2
arctan
2
2
wC i 1
i 1 y x0
1
1
2
2
2(i sin d ) 2(i sin x0 )
3 cos 2 y
sin y
dy
...
5
4
(i sin y )
x0 (i sin y )
d
2
33
34. Задержка шумом распада неустойчивого состояния
10.05
u( )
i=1.2
5.0
4
0.0
3
i=1.5
-5.0
2
-10.0
-10.0
-6.0
-2.0
2.0
6.0
10.0
0
1
2
3
4
5
Rylyakov A.V., Likharev K.K., Pulse jitter and timing errors in RSFQ circuits, IEEE Trans. Appl. Supercond.
Vol. 9,
2. - P. 3539-3544 (1999).
A.N. Malakhov, and A.L. Pankratov, Physica C, 269, 46 (1996).
A.L. Pankratov and B. Spagnolo, Phys. Rev. Lett., 93, 177001 (2004).
V.K. Semenov and A. Inamdar, IEEE Trans. Appl. Supercond., 15, 435 (2005).
A.V. Gordeeva and A.L. Pankratov, Appl. Phys. Lett., 88, 022505 (2006).
34
35.
,1
2 [ F ( 2 , 0 ) f 3 ( 2 , 0 )] ...
wC
3
10000
2
1000
1
100
i , =0.001
0
0.001
0.01
10
0.1
1
i , =0.001
1
0.1
0.01
1
1.2
1.4
1.6
1.8
2
i
35
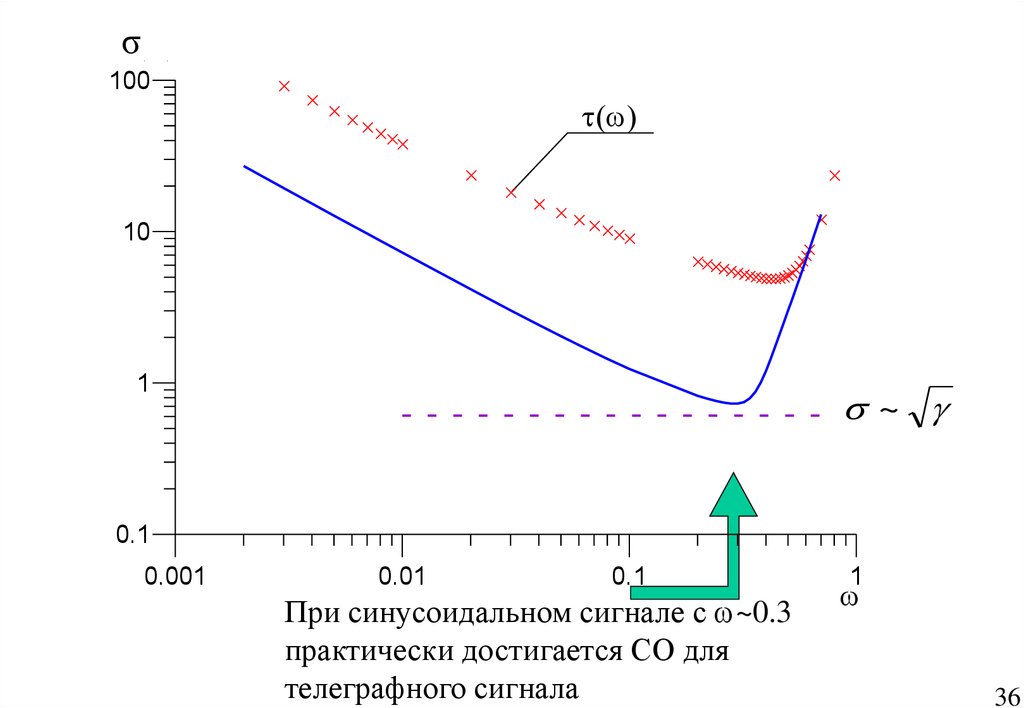
36.
σw
100
w
10
1
~
0.1
0.001
0.01
0.1
При синусоидальном сигнале с w~0.3
практически достигается СО для
телеграфного сигнала
1
w
36
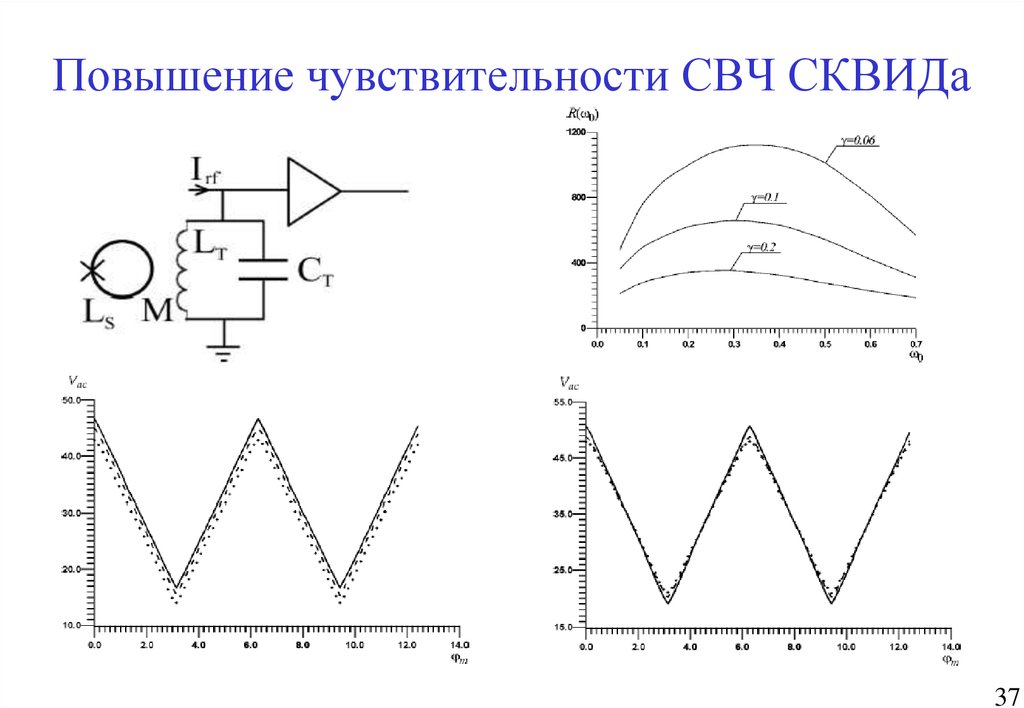
37. Повышение чувствительности СВЧ СКВИДа
3738.
Высокоскоростное переключениемагнитных диполей
Уравнение Ландау-Лифшица
dM
M M H eff
M
H
eff
1 2 M
dt
1 2
s
- гиромагнитная константа, - затухание
M s - намагниченность насыщения
H eff H a H e H T
2 kT
M sV
HT t; r 0
2
H i t ; r , H j t '; r ' 2 t t ' r r ' ij
2Ka
H a r 2 M r , na
Ms
38
39. Перемагничивание при различных углах
1.0Mx
0.5
0.0
-0.5
1.0
-1.0
-1.0
0.5
-0.5
0.0
0.0
M
y
-0.5
0.5
Mz
1.0 -1.0
39
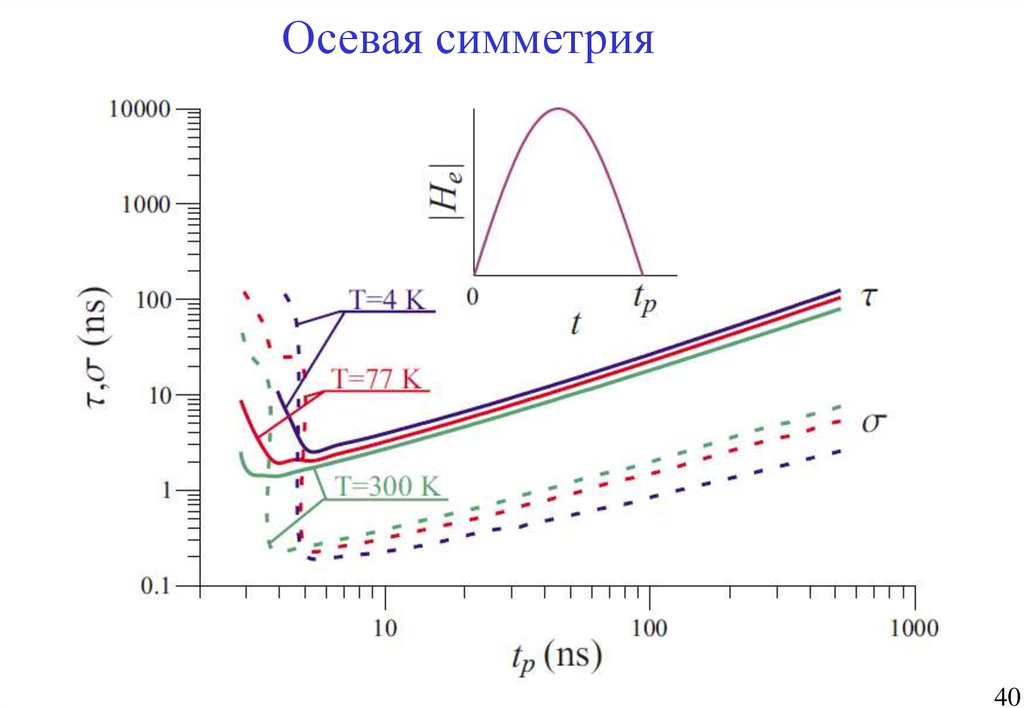
40.
Осевая симметрия40
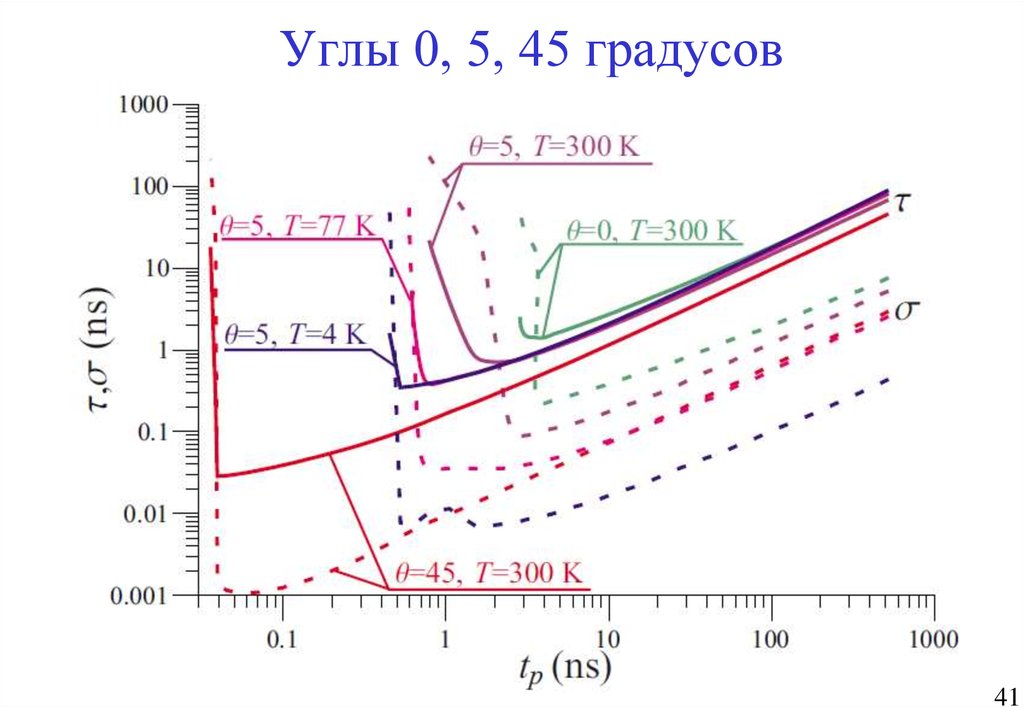
41. Углы 0, 5, 45 градусов
4142.
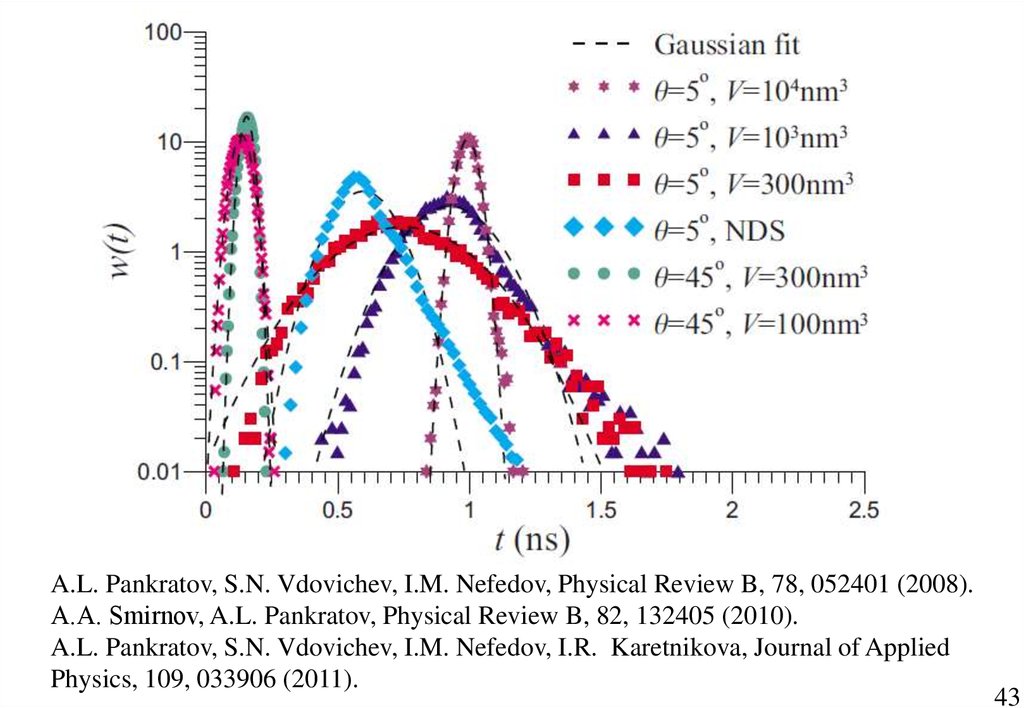
Зависимости от объёма частицы42
43.
A.L. Pankratov, S.N. Vdovichev, I.M. Nefedov, Physical Review B, 78, 052401 (2008).А.A. Smirnov, A.L. Pankratov, Physical Review B, 82, 132405 (2010).
A.L. Pankratov, S.N. Vdovichev, I.M. Nefedov, I.R. Karetnikova, Journal of Applied
Physics, 109, 033906 (2011).
43
44.
Оптимальное быстрое считываниесостояния кубита
( x, t )
2e 2 2 ( x, t ) V ( x, t )
i
( x, t )
2
t
C
x
V(x)
V(x)
|1>
|0>
x
x
44
45.
Эволюция вероятностиN P(t p ) Q(t p ) P10 P01,
P,Q
F 1 N
f(t)
1
P
0.1
tp[ns]
0.01
Q
0.001
0
Параметры:
2
4
6
8
t[ns]
Q. Zhang, A. G. Kofman, J. M. Martinis, and A. N. Korotkov,
Phys. Rev. B 74, 214518 (2006).
45
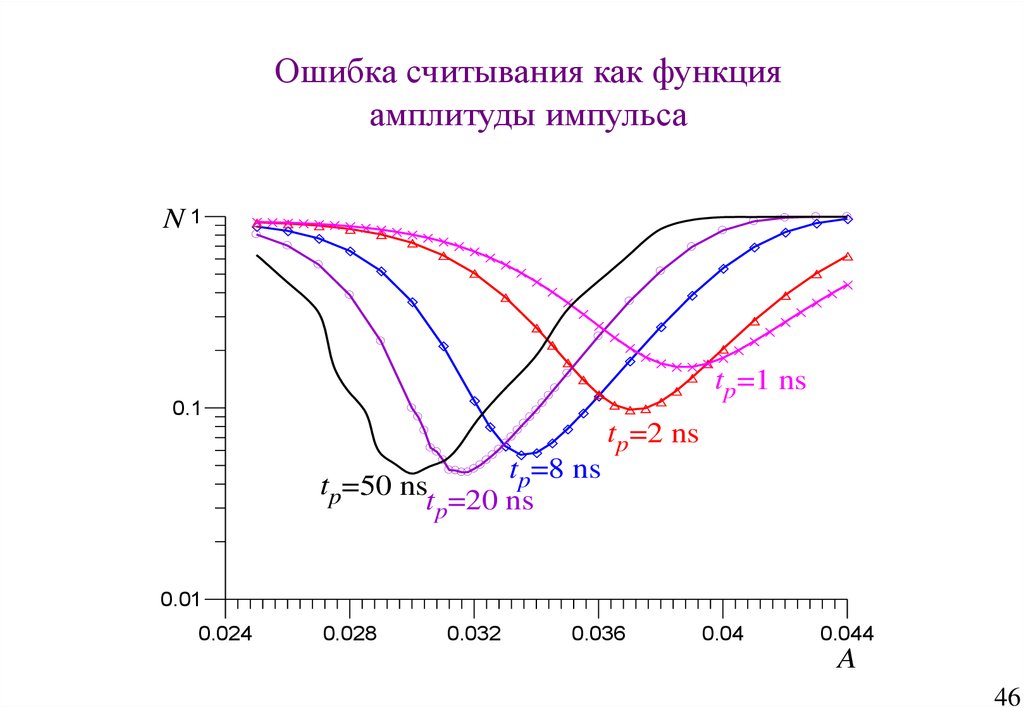
46.
Ошибка считывания как функцияамплитуды импульса
N1
tp=1 ns
0.1
tp=2 ns
tp=8 ns
tp=50 ns
tp=20 ns
0.01
0.024
0.028
0.032
0.036
0.04
0.044
A
46
47.
Ошибка считывания как функциядлительности импульса
N1
N
0.1
0.03
0.1
0.1
1
10
D[Hz]
A=0.012, D=3
A=0.019, D=2
A=0.0245, D=1.4
A=0.029, D=1
0.03
A=0.033, D=0.6933
1
10
100
tp[ns]
47
48.
Ошибка считывания как функцияглубины потенциальной ямы
N1
D=0.5
0.1
D=3
D=0.8
D=2.1
D=1.15
0.02
0.01
0.015
0.02
0.025
0.03
0.035
0.04
A
A.L. Pankratov and A.S. Gavrilov, Phys. Rev. B, 81, 052501 (2010).
L.S. Revin and A.L. Pankratov, Appl. Phys. Lett., 98, 162501 (2011).
48
49.
Модели нейроновМодель ФитцХью-Нагумо – двумерная модель, качественно описывающая способность
нервной клетки генерировать импульсы действия. Одна из переменных модели, x, носит
название переменной возбуждения (excitation variable) и имеет быстрый характер изменения
во времени. Другая – восстанавливающая (recovery variable) переменная y – изменяется медленно:
x F ( x, y) x x 3 / 3 y
y G( x, y) ( x I )
Фазовый портрет автономной системы ФитцХьюНагумо. Синим цветом изображены изоклины
горизонтальных и вертикальных наклонов; красным –
линия, разделяющая потоки траекторий. Возможные
фазовые траектории, полученные при различных
начальных условиях, изображены зеленым цветом.
49
50.
Модель Ходжкина-Хаксли – четырехмерная модель нервной клетки, описывающаявозбудимые свойства мембран с помощью уравнений баланса ионных токов через мембрану.
dv
GK n 4 (v v K ) G Na m 3 h(v v Na ) GL (v v L ) S (t ) (t );
dt
dm
dh
dn
m (1 m) m m;
h (1 h) h h;
n (1 n) n n.
dt
dt
dt
Cm
Здесь v задает отклонение мембранного потенциала от равновесного состояния (V =Veq+v). Шум
(t) - белый гауссов с нулевым средним и корреляционной функцией < (t) (t+ )>=D ( ).
Влияние шума на возникновение спайков в системе рассматривается в условиях существования
внешнего надпорогового периодического воздействия S(t)=Asin(2 ft+ 0).
Значения параметров максимальных проводимостей для натриевого, калиевого каналов и канала
утечки соответственно равны:
GNa = 120 mS/cm2, GK = 36 mS/cm2, GL = 0.3 mS/cm2 ;
Емкость мембраны Cm = 1 µF/cm2.
Равновесные потенциалы: vNa = 115mV , vK = -12 mV , vL = 10.6 mV.
В результате анализа кинетических кривых активации и инактивации А. Ходжкиным и А. Хаксли
были построены графические зависимости скоростей m, m, n, n, h, h от мембранного
потенциала и подобраны эмпирические соотношения, описывающие ход указанных зависимостей:
0.1(25 v)
0.01(10 v)
v
; n
; h 0.07 exp{ };
exp{( 25 v) / 10} 1
exp{(10 v) / 10} 1
20
v
v
m 4 exp{ }; n 0.125 exp{ }; h (exp{( 30 v) / 10} 1) 1 ;
80
80
m
50
51.
Когерентный резонансPikovsky AS, Kurths J, Coherence resonance in a noise-driven excitable system.
Physical Review Letters 78:775-778 (1997).
51
52.
Подавление шума в нейронных системах52
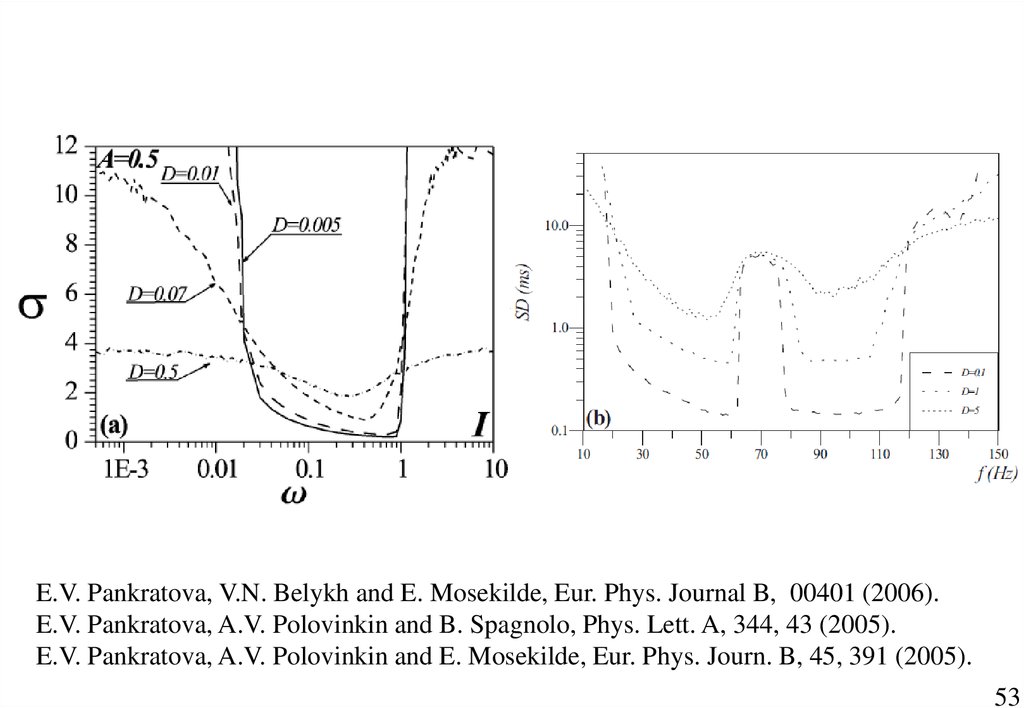
53.
E.V. Pankratova, V.N. Belykh and E. Mosekilde, Eur. Phys. Journal B, 00401 (2006).E.V. Pankratova, A.V. Polovinkin and B. Spagnolo, Phys. Lett. A, 344, 43 (2005).
E.V. Pankratova, A.V. Polovinkin and E. Mosekilde, Eur. Phys. Journ. B, 45, 391 (2005).
53
54.
Спасибо завнимание!
54
55.
5556.
5657.
100S(w
10
1
0.1
0.01
0.001
1.0
2.0
3.0
4.0
5.0
6.0
7.0
w
57


















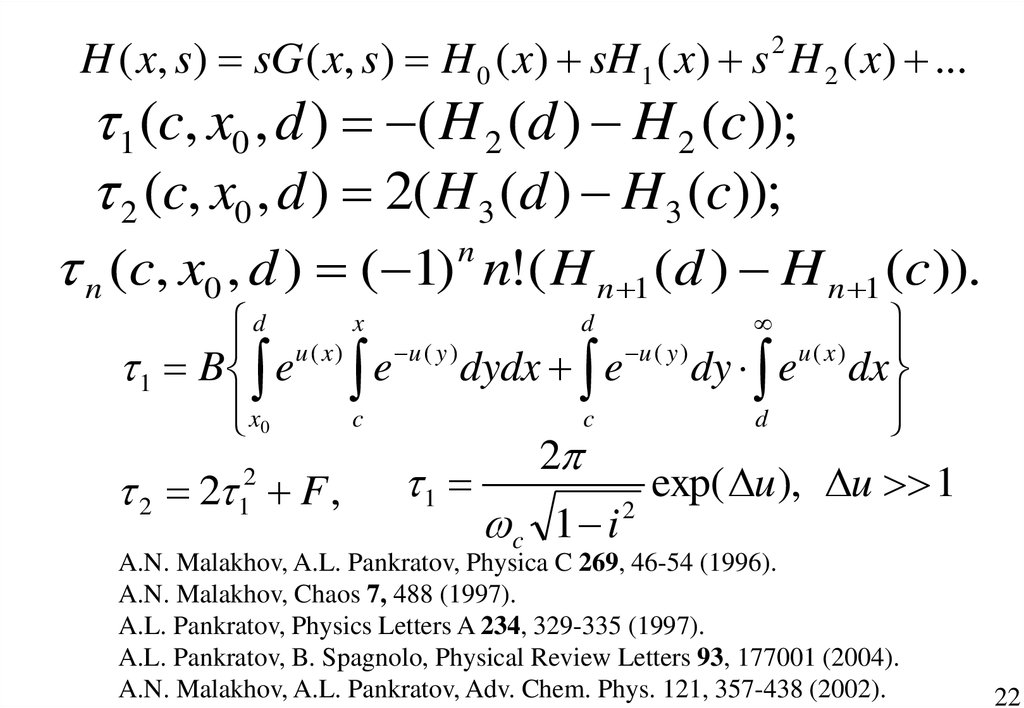
























 Физика
Физика








