Похожие презентации:
Способы построения и практическое применение замечательных кривых
1.
МОУ «Лицей № 3 Тракторозаводского района Волгограда»Открытый городской конкурс
учебно-исследовательских работ старшеклассников
в рамках городского научного общества «Я и Земля»
Секция математики
СПОСОБЫ ПОСТРОЕНИЯ И
ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ЗАМЕЧАТЕЛЬНЫХ КРИВЫХ
Выполнили:
Савенко Елизавета Витальевна,
Тарлыгина Дарья Александровна,
учащиеся 9«В» класса
Руководители:
Смыковская Татьяна Константиновна,
д-р пед. наук, проф. ВГСПУ,
Савенко Жанна Викторовна,
учитель математики МОУ Лицей №3
2.
Объект исследования:замечательные кривые.
Предмет исследования:
практическое применение замечательных кривых.
Цель исследования: систематизировать
знания о замечательных кривых, способах
их построения и практическом применении.
3.
Задачи исследования:1. Найти и изучить информацию по теории
замечательных кривых.
2. Провести опыты, показывающие способ
построения конкретной замечательной кривой.
3. Показать возможности применения
замечательных кривых в технике и жизни и их
существования в природе.
4.
Задача № 1 исследования:Найти и изучить информацию по теории
замечательных кривых.
5.
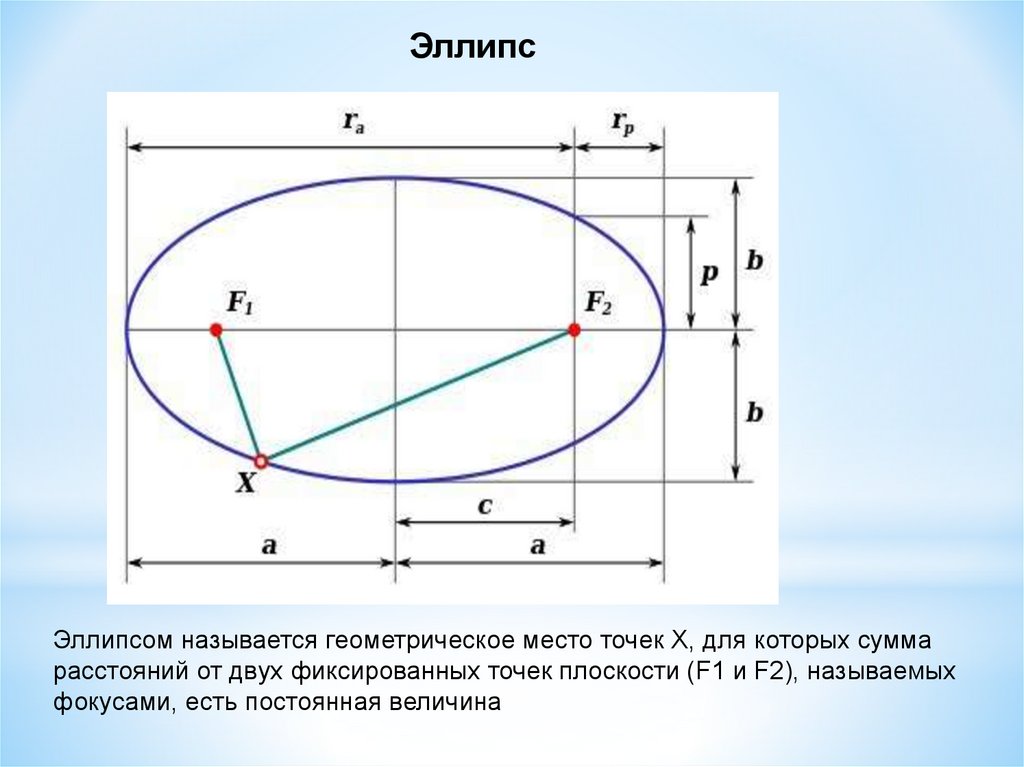
ЭллипсЭллипсом называется геометрическое место точек Х, для которых сумма
расстояний от двух фиксированных точек плоскости (F1 и F2), называемых
фокусами, есть постоянная величина
6.
Свойства эллипсаАкустический эффект в пещере эллиптической формы
7.
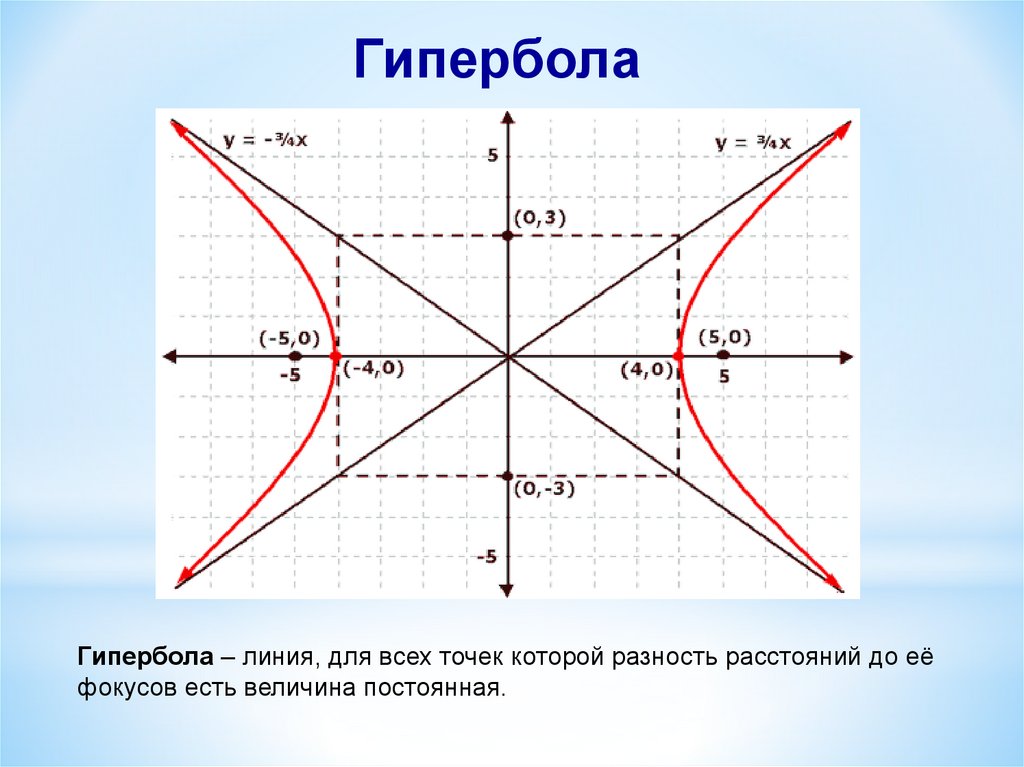
ГиперболаГипербола – линия, для всех точек которой разность расстояний до её
фокусов есть величина постоянная.
8.
Свойства гиперболыЗона слышимости звука пролетающего самолета
9.
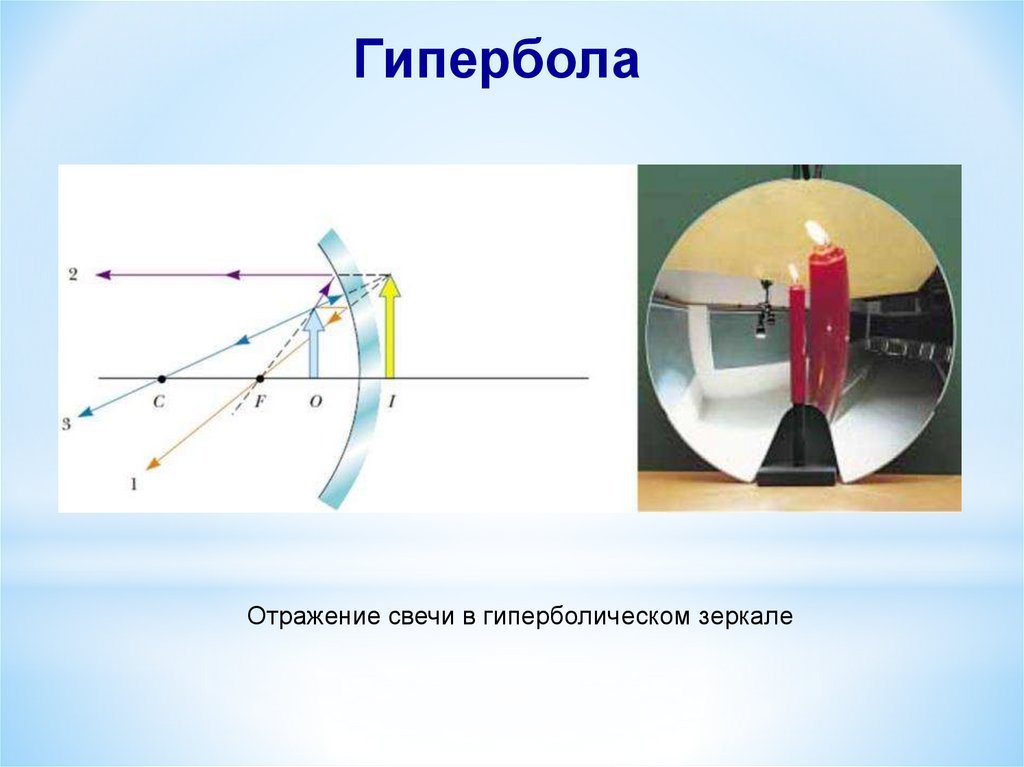
ГиперболаОтражение свечи в гиперболическом зеркале
10.
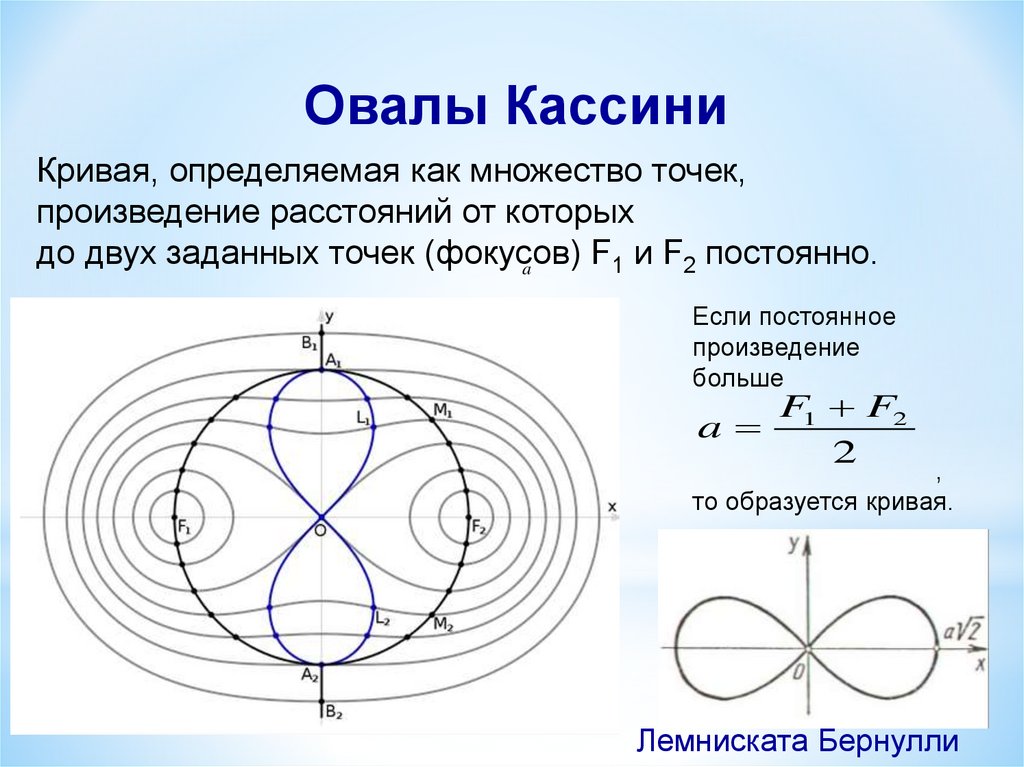
Овалы КассиниКривая, определяемая как множество точек,
произведение расстояний от которых
до двух заданных точек (фокусов)
F1 и F2 постоянно.
a
Если постоянное
произведение
больше
a
F1 F2
2
,
то образуется кривая.
Лемниската Бернулли
11.
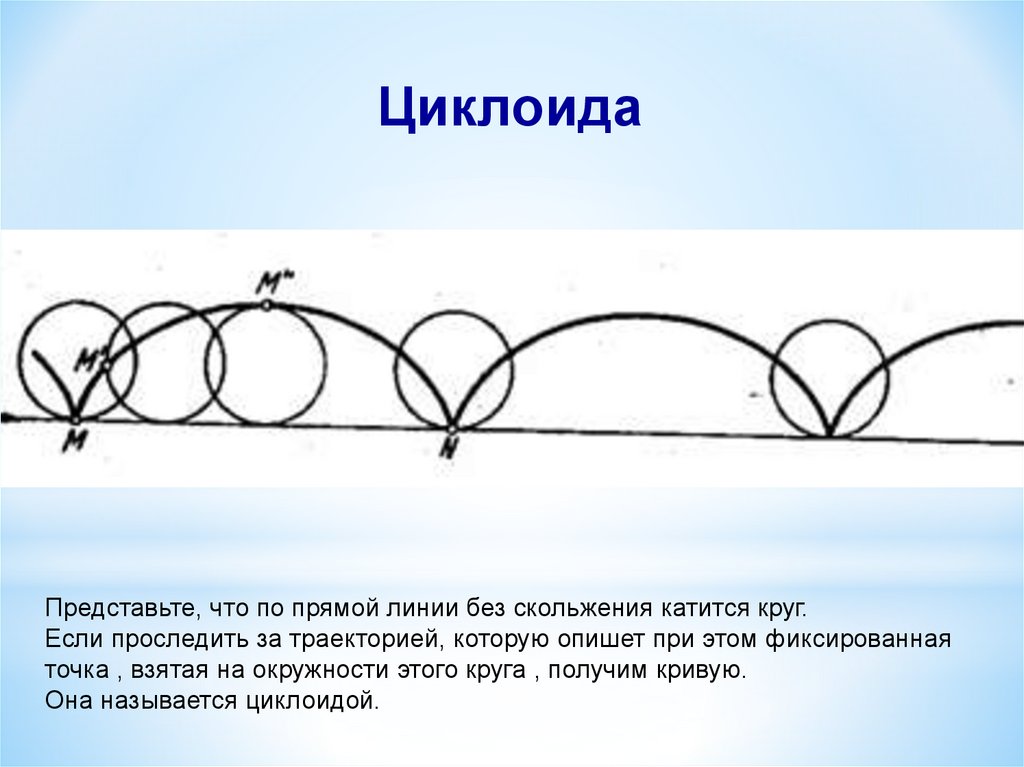
ЦиклоидаПредставьте, что по прямой линии без скольжения катится круг.
Если проследить за траекторией, которую опишет при этом фиксированная
точка , взятая на окружности этого круга , получим кривую.
Она называется циклоидой.
12.
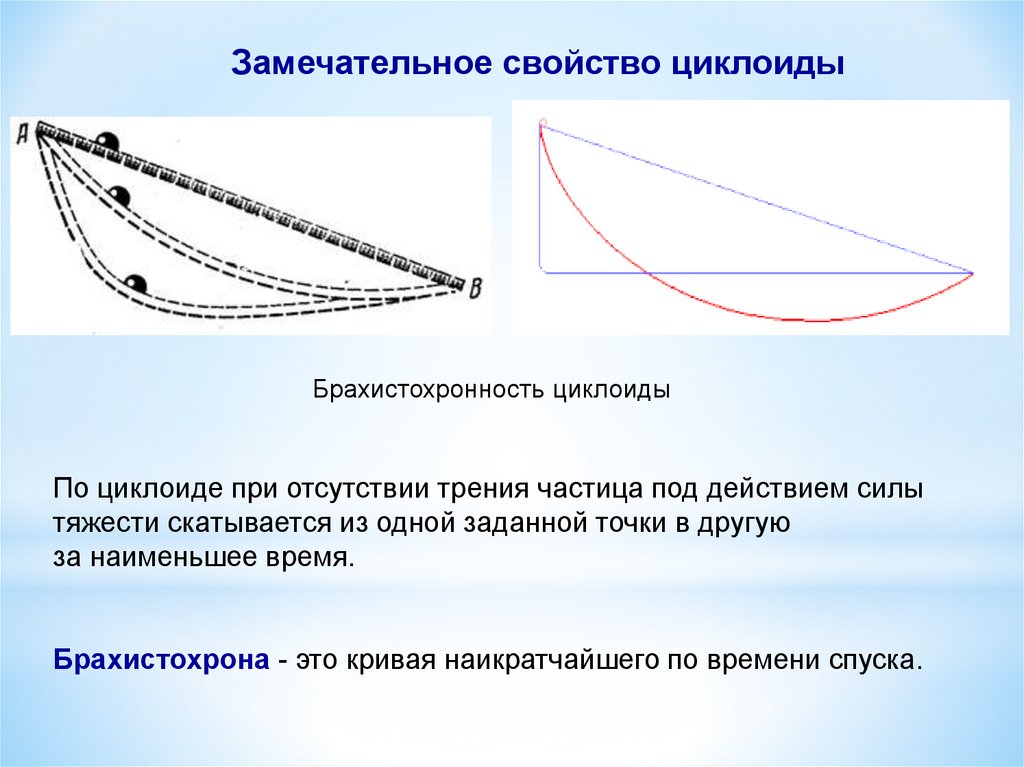
Замечательное свойство циклоидыБрахистохронность циклоиды
По циклоиде при отсутствии трения частица под действием силы
тяжести скатывается из одной заданной точки в другую
за наименьшее время.
Брахистохрона - это кривая наикратчайшего по времени спуска.
13.
«Спираль Архимеда»Спираль Архимеда - это плоская кривая, которую вырисовывает точка,
движущаяся с постоянной скоростью от центра окружности по ее радиусу.
Увеличение ее шага, всегда равномерно.
14.
Задача № 2 исследования:Провести опыты, показывающие способ
построения конкретной замечательной кривой
15.
Эллипс16.
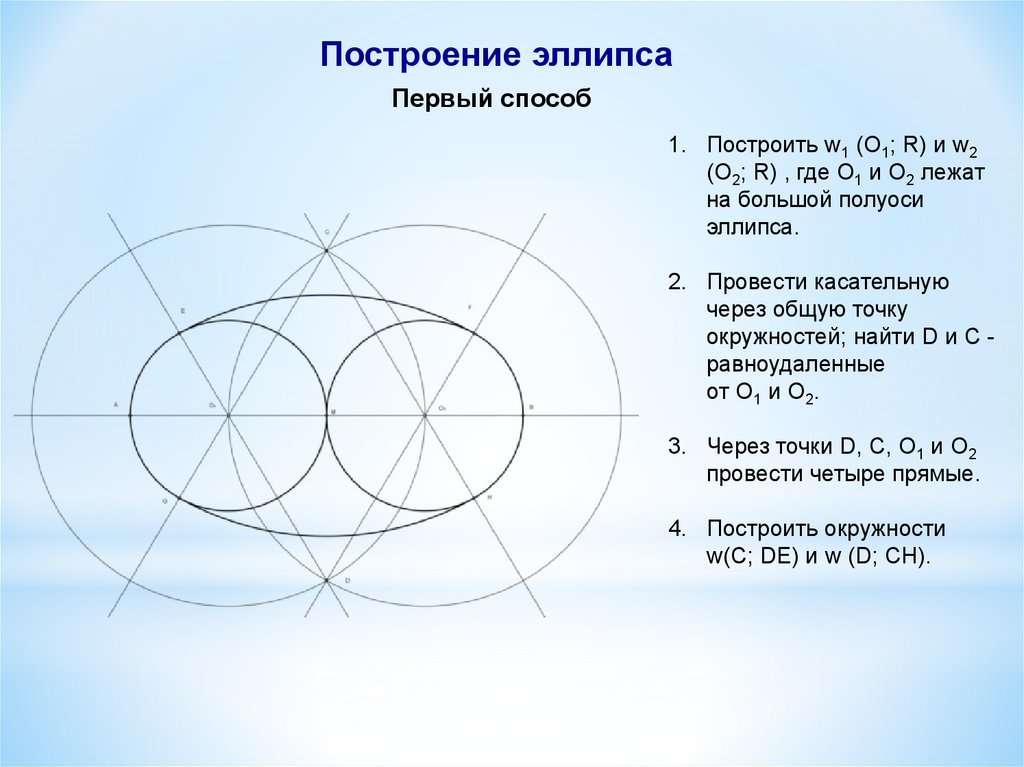
Построение эллипсаПервый способ
1. Построить w1 (O1; R) и w2
(O2; R) , где O1 и O2 лежат
на большой полуоси
эллипса.
2. Провести касательную
через общую точку
окружностей; найти D и C равноудаленные
от O1 и О2.
3. Через точки D, C, O1 и O2
провести четыре прямые.
4. Построить окружности
w(C; DE) и w (D; CH).
17.
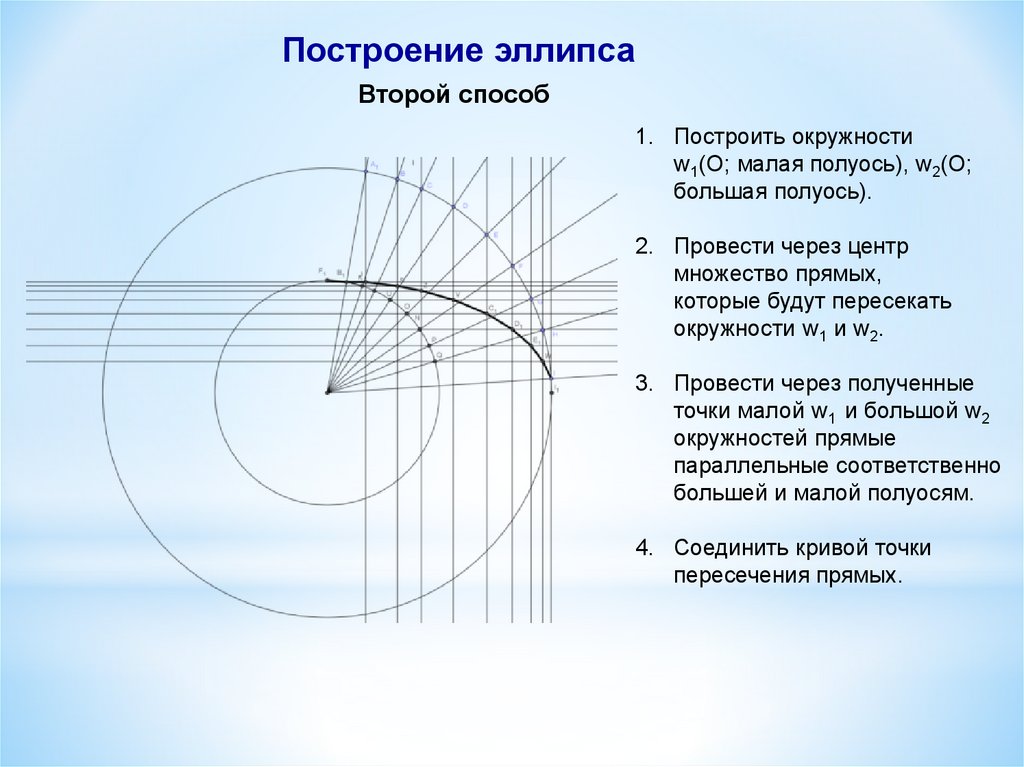
Построение эллипсаВторой способ
1. Построить окружности
w1(О; малая полуось), w2(O;
большая полуось).
2. Провести через центр
множество прямых,
которые будут пересекать
окружности w1 и w2.
3. Провести через полученные
точки малой w1 и большой w2
окружностей прямые
параллельные соответственно
большей и малой полуосям.
4. Соединить кривой точки
пересечения прямых.
18.
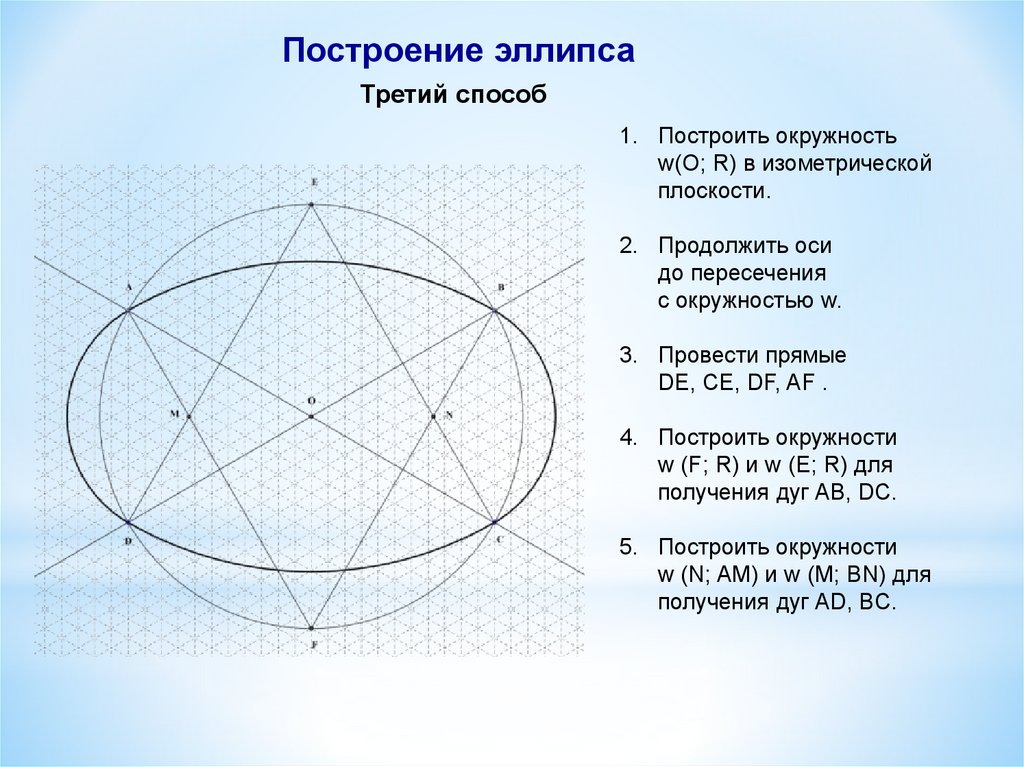
Построение эллипсаТретий способ
1. Построить окружность
w(О; R) в изометрической
плоскости.
2. Продолжить оси
до пересечения
с окружностью w.
3. Провести прямые
DE, CE, DF, AF .
4. Построить окружности
w (F; R) и w (E; R) для
получения дуг AB, DC.
5. Построить окружности
w (N; AM) и w (M; BN) для
получения дуг AD, BC.
19.
Построение циклоиды20.
Построение гиперболыНужно взять линейку, нить и три кнопки.
Две кнопки воткнуть в лист бумаги – в
этих точках будут фокусы гиперболы – и
к ним привязать концы нити. Третью
кнопку втыкают в линейку около ее края,
привязав к ней нить недалеко от
середины нити, но не в середине. Если
теперь, прижимая нить к краю линейки
кончиком карандаша и держа нить все
время в натянутом состоянии, двигать
карандаш, то его графит будет
вычерчивать на бумаге одну из ветвей
гиперболы
21.
Входе
анализа
литературы
и
при проведении опытов было установлено,
что
кривая
есть
след
движущейся
(острие карандаша, монета и т.д.)
точки
22.
Задача № 3 исследования:Показать возможности применения
замечательных кривых в технике и жизни,
их существования в природе.
23.
ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ В ЖИЗНИ ЧЕЛОВЕКА24.
Практическая ценностьрезультатов исследования:
представлены способы построения отдельных
замечательных кривых;
показано использование замечательных кривых
в природе и технике.
25.
Интерес к кривым обусловленне только их красотой и оригинальностью,
но и большой практической ценностью.
Кривые имеют непосредственное отношение
к окружающему нас миру.
Они имеют место в природе, науке, архитектуре.
В дальнейшем мы предполагаем изучить другие виды
замечательных кривых.
















 Инженерная графика
Инженерная графика








