Похожие презентации:
Замечательные кривые
1.
Замечательныекривые
2.
Замечательные кривыеПроект по геометрии
Выполнил Кузин Михаил
Ученик 9 Б класса МОУ СОШ №4
г.Михайловска
Руководитель Романенко О.С.
2011 год
3.
Цели и задачиo познакомить учащихся с
дополнительными материалами по
теме;
oизучить построение кривых на
примере циклоиды, помочь разобраться
со схемой построения кривых;
oРасширить кругозор по теме
«Графики»;
oСделать вывод по предложенной
гипотезе
4.
ГипотезаСуществует ли
практическое применение
кривых
5.
Природа говорит языкомматематики: буквы этого языка –
круги, треугольники и иные
математические фигуры.
Г. Галилей
6.
Краткая аннотация проектаВ основе проекта изучение темы «Кривые"
курса геометрии направлен на развитие
познавательных способностей, навыков
самостоятельной работы.
В проекте затронуты учебные темы:
«Построение геометрических фигур»,
«Графики функций».
7.
Замечательные кривыеЗовут меня ученые - кривая.
Я - линия довольно не простая:
Есть у меня изгибы, повороты,
И есть прямые слуги асимптоты.
Прямая ломит напролом, ломая шею.
Я ж обойти преграды все сумею,
А максимум и минимум известны
Кривую делает особо интересной
И как не хорохорится прямая,
Довольно точна линия такая
Представит синусоиду простую,
Взять только амплитуду нулевую.
И коль соображаешь ты, братишка,
Тогда при мне не задавайся слишком
Ведь знают все детсадовцы любые,
Что в голове извилины кривые!
Но, между прочим, и для разгильдяя
Живет во мне надежда неплохая:
Лентяй из двоек вылезет,
Когда «кривая вывезет».
8.
Виды кривыхэллипс
циклоида
парабола
трактриса
спираль
9.
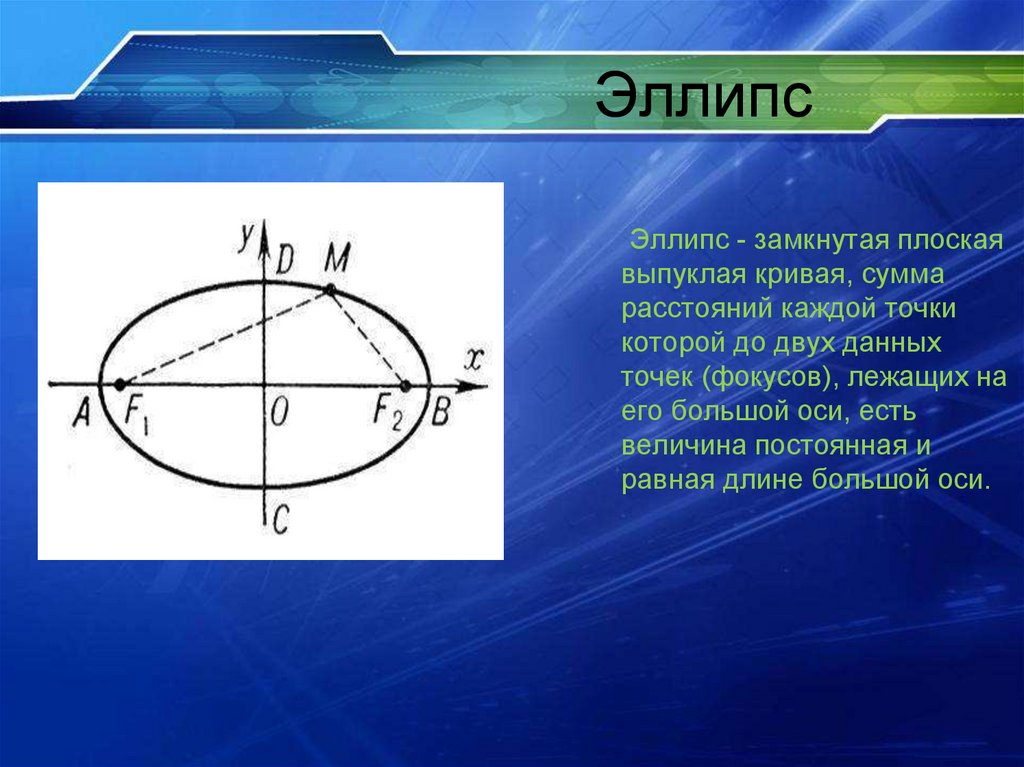
ЭллипсЭллипс - замкнутая плоская
выпуклая кривая, сумма
расстояний каждой точки
которой до двух данных
точек (фокусов), лежащих на
его большой оси, есть
величина постоянная и
равная длине большой оси.
10.
Построение эллипса1.Проводят две перпендикулярные
осевые линии;
2.От точки их пересечения
откладывают вверх и вниз по
вертикальной оси отрезки, равные длине
малой полуоси, а влево и вправо по
горизонтальной оси - отрезки, равные
длине большой полуоси получаем точки
A,B,C и D;
3.Проводим две концентрические
окружности диаметрами AB и CD;
4.Проводим ряд лучей диаметров;
5.Из точек пересечения лучей с
окружностями проводят линии,
параллельные осям эллипса, до
взаимного пересечения в точках,
принадлежащих эллипсу;
6.Полученные точки соединяют
плавной кривой.
11.
ЦиклоидаКривая, которую описывает точка, закрепленная на окружности, катящейся
без скольжения по прямой линии, называется циклоидой.
12.
Галилео Галилей13.
Спираль АрхимедаСпираль Архимеда плоская кривая,
которую описывает
точка, движущаяся
равномернопоступательно от
центра 0 по
равномерновращающемуся
радиусу.
14.
Построение Архимедовойспирали
• Из центра 0 проводят окружность радиусом, равным шагу S
спирали и делят шаг и окружность на несколько равных частей
Точки деления нумеруют;
• Из центра 0 радиусами 01, 02, 03, ... проводят дуги до
пересечения с соответствующими радиусами в точках I, II, III, ...;
• Полученные точки принадлежат спирали Архимеда с заданным
шагом S и центром 0.
15.
Архимед - механик• Архимед (287 до н. э. — 212
до н. э.) — древнегреческий
математик, механик и
инженер из Сиракуз. Отцом
его был астроном Фидий,
который привил сыну с
детства любовь к
математике, механике и
астрономии. Архимед
родился в Сиракузах (о.
Сицилия) и жил в этом
городе в эпоху 1-й и 2-й
Пунических войн. Научную
деятельность начал как
механик и техник.
16.
Архимедовы спиралиПервые труды Архимеда были
посвящены механике. Принцип рычага,
учение о центре тяжести и закон
Архимеда являются важнейшими
достижениями Архимеда в области
механики. Архимед был не только
математиком и механиком, но и одним
из крупнейших инженеров и
конструкторов своего времени. Машина
для поливки полей "Улитка",
водоподъемный винт (винт Архимеда),
разнообразные военные машины для
метания копий и дротиков, для
поднятия и потопления кораблей
увековечили славу Архимеда.
17.
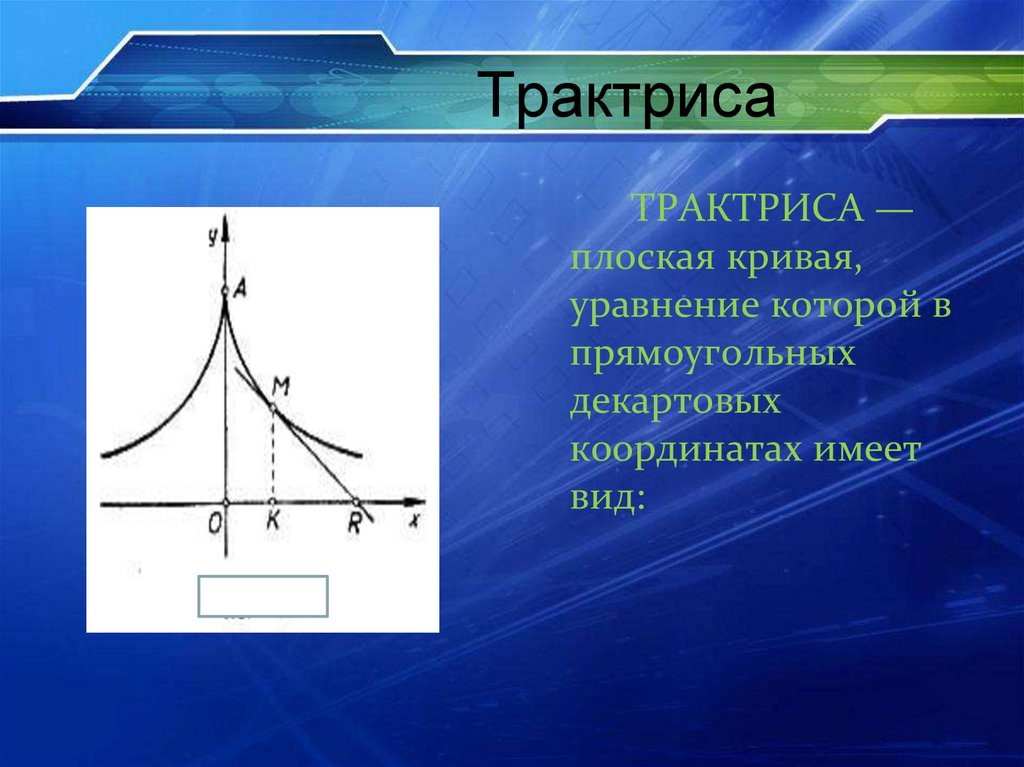
ТрактрисаТРАКТРИСА —
плоская кривая,
уравнение которой в
прямоугольных
декартовых
координатах имеет
вид:
18.
Трактриса• Расположим в
горизонтальной плоскости
натянутую гибкую
нерастяжимую нить, к
одному концу которой
прикреплен груз. Другой её
конец будем перемещать
вдоль прямой, лежащей
одной плоскости и не
совпадающей с
направлением нити. Эту
задачу в 1693 г. поставил
французский архитектор
Клод Перро- брат
знаменитого сказочника
Шарля Перро
19.
Парабола• Пара́бола (греч. παραβολή —
приложение) —
геометрическое место точек,
равноудалённых от данной
прямой (называемой
директрисой параболы) и
данной точки (называемой
фокусом параболы).
• Наряду с эллипсом и
гиперболой, парабола
является коническим
сечением. Она может быть
определена как коническое
сечение с единичным
эксцентриситетом.
20.
ГиперболаГипе́рбола — от
греч.«бросать»и«сверх»—
геометрическое место точек
M Евклидовой плоскости,
для которых абсолютное
значение разности
расстояний от M до двух
выделенных точек F1 и F2
(называемых фокусами)
постоянно. Точнее,
причем | F1F2 | > 2a > 0.
21.
Циклоида• Цикло́ида — круглый) —
плоская
трансцендентная
кривая. Циклоида
определяется
кинематически как
траектория
фиксированной точки
производящей
окружности радиуса r,
катящейся без
скольжения по прямой.
22.
ГаллилейГалиле́о Галиле́й (1564-1642 ) —
итальянский физик, механик,
астроном, философ и
математик, оказавший
значительное влияние на науку
своего времени.
Галилей — основатель
экспериментальтной физики
Термин "циклоида" предложил Г.
Галилей (ок.1598).
23.
Декартов лист• Кривая, заданная
уравнением
х3+у3=3аху
называется
декартовым
листом
24.
ДекартРене Декарт (1596-1650),
французский философ, математик,
физик и физиолог. С 1629 в
Нидерландах. Заложил основы
аналитической геометрии,
В область изучения геометрии Декарт
включил «геометрические» линии
(позднее названные Лейбницем
алгебраическими) — линии,
описываемые при движении
шарнирными механизмами.
Трансцендентные кривые (сам Декарт
называет их «механическими») он
исключил из своей геометрии.
25.
Кривые вокруг нас26.
Выводы по проектуСчитаю, что дополнительно
нужно изучать свойства кривых и
этот проект может служить
методическим пособием для
желающих самостоятельно овладеть
теоретическими знаниями в данной
области.
























 Инженерная графика
Инженерная графика








