Биномиальные кучи

1.

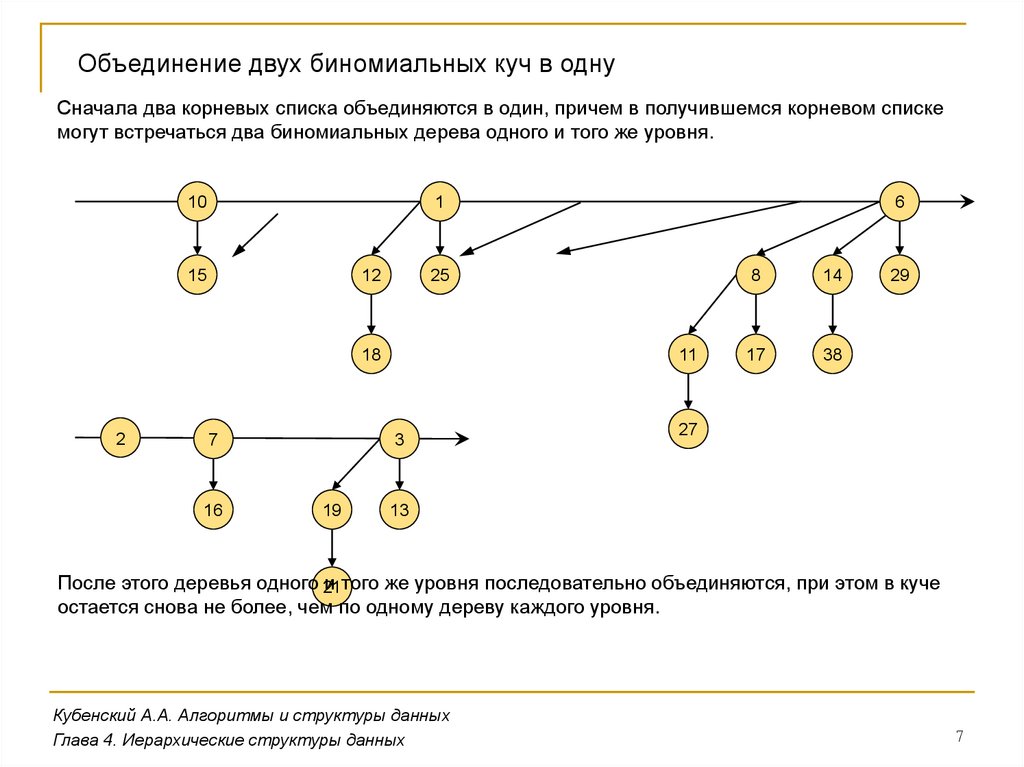
Биномиальные кучи
Двоичные кучи имеют один существенный недостаток: невозможно быстро объединить две
двоичные кучи в одну. Такое объединение происходит со скоростью O(N log M), где N – размер
добавляемой кучи, а M – размер исходной кучи.
Если в алгоритме используется операция объединения куч, то лучше использовать
биномиальные кучи, для которых эта операция выполняется со скоростью порядка O(log N).
Биномиальные деревья
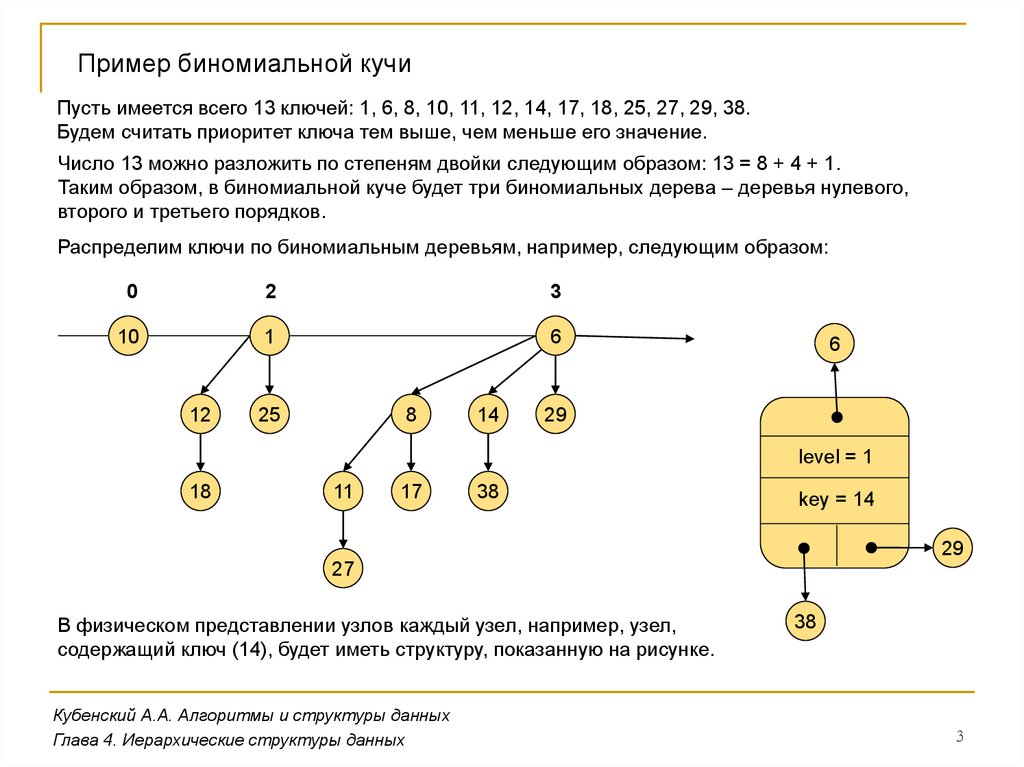
Биномиальная куча состоит из биномиальных деревьев, каждое из которых содержит 2k узлов.
Таким образом, если требуется хранить N значений, то число N раскладывается по степеням
двойки, и образуются биномиальные деревья с соответствующим количеством узлов в каждом.
Биномиальная куча представляет собой список таких деревьев.
25 = 16 + 8 + 1
1
8
16
Кубенский А.А. Алгоритмы и структуры данных
Глава 4. Иерархические структуры данных
1

2.

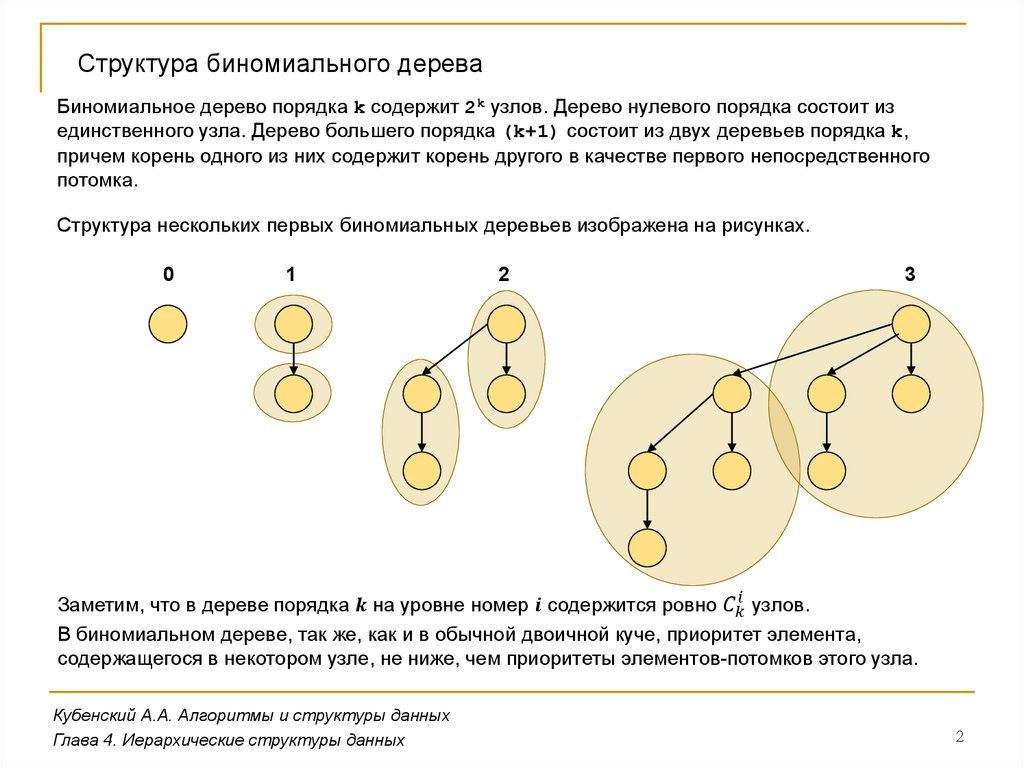
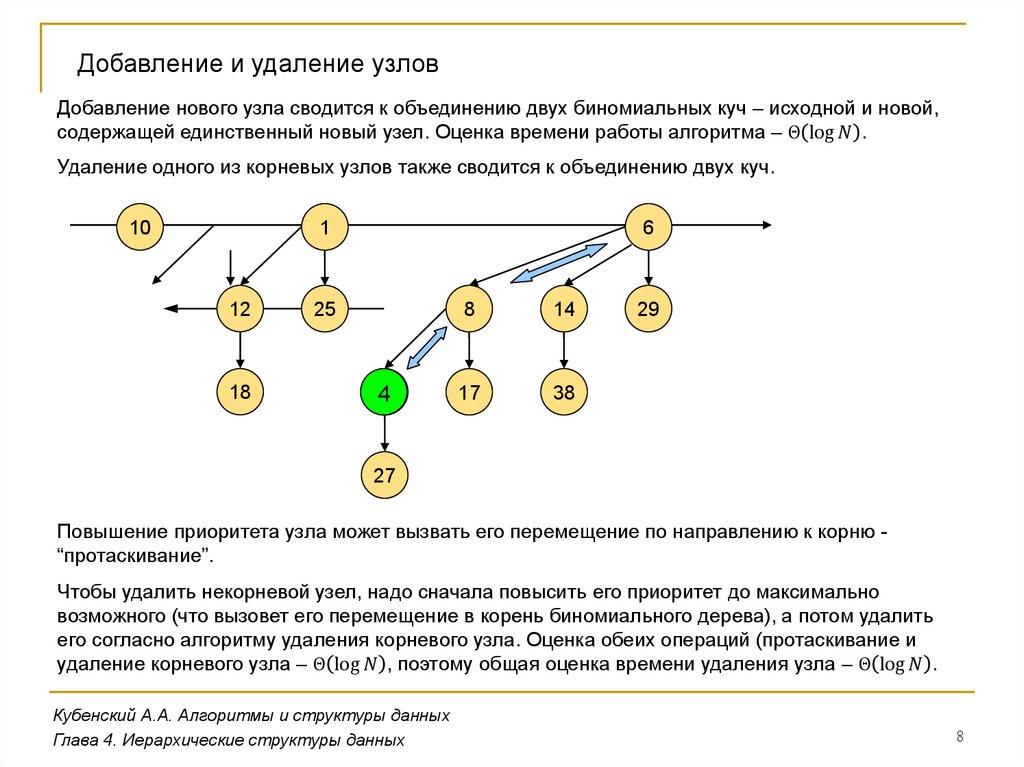
Структура биномиального дерева
Биномиальное дерево порядка k содержит 2k узлов. Дерево нулевого порядка состоит из
единственного узла. Дерево большего порядка (k+1) состоит из двух деревьев порядка k,
причем корень одного из них содержит корень другого в качестве первого непосредственного
потомка.
Структура нескольких первых биномиальных деревьев изображена на рисунках.
0
1
2
3
Заметим, что в дереве порядка