Сортировка выбором

1.

СОРТИРОВКА
ВЫБОРОМ
ИВТБ-1301

2.

ПРИНЦИП РАБОТЫ
• Просто и незатейливо — проходим по
массиву в поисках максимального
элемента. Найденный максимум меняем
местами с последним элементом.
Неотсортированная часть массива
уменьшилась на один элемент (не
включает последний элемент, куда мы
переставили найденный максимум). К
этой неотсортированной части
применяем те же действия — находим
максимум и ставим его на последнее
место в неотсортированной части
массива. И так продолжаем до тех пор,
пока неотсортированная часть массива
не уменьшится до одного элемента

3.

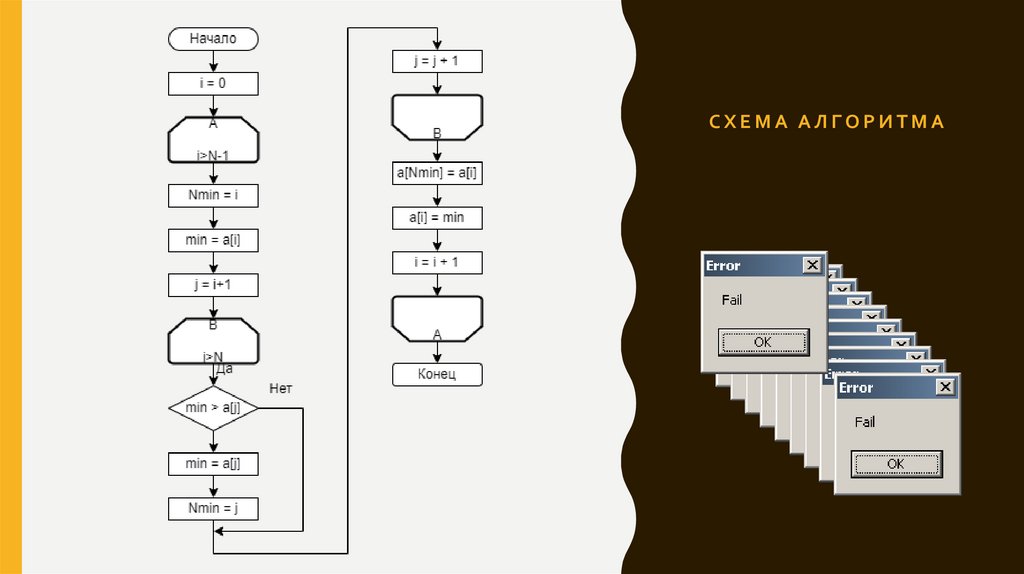
СХЕМА АЛГОРИТМА

4.

ВРЕМЯ РАБОТЫ И
ЭФФЕКТИВНОСТЬ СОРТИРОВКИ
• Лучшее, время работы сортировки
массива методом выбора – О(n), где n –
количество элементов массива
• Среднее и худшее время работы
вычисляется по формуле O(n^2), где n
– количество элементов массива
• Сортировка выбором является
эффективной сортировкой для
небольших массивов. Для больших
массивов она может быть
неэффективна, так как ее время
работы в худшем случае составляет
O(n^2)

5.

ПАМЯТЬ И УСТОЙЧИВОСТЬ
• Пространственная сложность сортировки
выбором составляет O(1). Это означает,
что сортировка выбором использует
только постоянную (не зависящую от
размера входного массива)
дополнительную память.
• В частности, сортировка выбором
использует только переменные,
необходимые для хранения индекса
текущего элемента и наименьшего
элемента, найденного до текущего
момента.
• Сортировка выбором является стабильной
сортировкой, то есть элементы, равные по
значению, остаются в том же порядке, в
котором они находились до сортировки.
• Это достигается за счет того, что
сортировка выбором не меняет порядок
элементов, равных по значению. На
каждом шаге сортировки выбором
выбирается наименьший элемент из
оставшейся части массива. Если этот
элемент равен текущему, то он не
обменивается местами с текущим
элементом.

6.

КОЛИЧЕСТВО ОБМЕНОВ И
ДЕТЕРМИНИРОВАННОСТЬ
• Количество обменов, выполняемых сортировкой
выбором, зависит от исходного порядка элементов
в массиве. В худшем случае, когда элементы
массива отсортированы в обратном порядке,
сортировка выбором выполняет n-1 обменов.
• В среднем случае, когда элементы массива
распределены равномерно, сортировка выбором
выполняет (n^2)/2 обменов.
• В лучшем случае, когда элементы массива уже
отсортированы, сортировка выбором не
выполняет ни одного обмена.
• Таким образом, количество обменов сортировки
выбором может быть от 0 до n-1.
• Сортировка выбором является
детерминированным
алгоритмом, то есть ее результат
не зависит от порядка
следования операций. Это
означает, что при одинаковых
входных данных сортировка
выбором всегда даст одинаковый
результат.

7.

ВСЕМ СПАСИБО, ВСЕ МОЛОДЦЫ