Основы теории тепловых двигателей. Термодинамика потока

1.

Теплотехника ПНИПУ
Основы теории
тепловых двигателей
Термодинамика потока
© 2002-2023 WebMaster [email protected]

2.

Теплотехника ПНИПУ
Первый закон термодинамики для потока
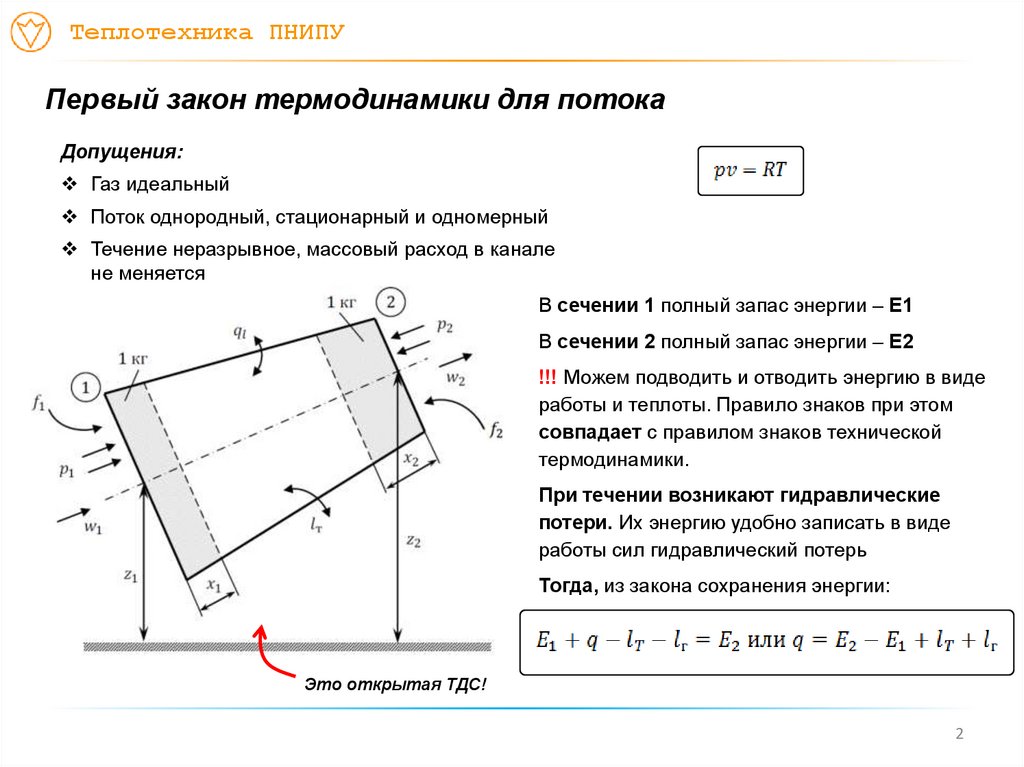
Допущения:
Газ идеальный
Поток однородный, стационарный и одномерный
Течение неразрывное, массовый расход в канале
не меняется
В сечении 1 полный запас энергии – Е1
В сечении 2 полный запас энергии – Е2
!!! Можем подводить и отводить энергию в виде
работы и теплоты. Правило знаков при этом
совпадает с правилом знаков технической
термодинамики.
При течении возникают гидравлические
потери. Их энергию удобно записать в виде
работы сил гидравлический потерь
Тогда, из закона сохранения энергии:
Это открытая ТДС!
2

3.

Теплотехника ПНИПУ
Первый закон термодинамики для потока
Полный запас энергии с учетом замечаний о гидравлических
потерях:
потенциальная энергия
положения
внутренняя энергия
потенциальная энергия
сил давления
кинетическая энергия
движения потока
газ во входном сечении получает
дополнительную энергию
Позади движущийся
поток
Впереди
движущаяся
масса
Рабочее тело преодолевает
сопротивление
3

4.

Теплотехника ПНИПУ
Первый закон термодинамики для потока
Подставим энергию по сечениям в уравнения для количества теплоты:
изменение энтальпии
работа проталкивания
ПЕРВЫЙ
ЗАКОН
ВАЖНО: все параметры состояния потока
определяются на границах термодинамической
системы
Для идеального газа!
4

5.

Теплотехника ПНИПУ
Первый закон. Механическая форма
Механическая форма первого закона термодинамики позволяет избавиться от тепловых величин.
1. Свяжем систему координат с потоком (СК начнет двигаться вместе с частицами).
2. Используем первый закон ТД для закрытой системы.
dq di v dp
w2
d ql d i d g dz d lT .
2
Заменяем теплоту и энтальпию, используя энергетическую форму
Распространение уравнений Бернулли
на случай течения сжимаемой вязкой
жидкости (газа).
Располагаемая работа газа. Учитывает
все тепловое влияние на поток.
Этими вещами часто
пренебрегают.
Для идеального газа:
5

6.

Теплотехника ПНИПУ
Параметры торможения
Это параметры состояния потока (давление, температура, удельный объем) при мгновенной его
остановке.
Обозначаются индексом
*
Для идеального газа все параметры можно выразить из энергетической формы Первого закона ТД:
тормозим поток в сечении 2 и получаем:
!
Температура торможения выше действительной температуры из-за
превращения кинетической энергии в энтальпию при остановке потока.
Проблема «теплового барьера»
6

7.

Теплотехника ПНИПУ
Параметры торможения
Тепловой барьер или аэродинамический нагрев – проблема разогрева тела, движущегося в потоке
газа при М > 1.
Некоторые трудности, вызываемые данной проблемой:
невозможность измерить действительную температуру как потока, так и тела в потоке
обычными датчиками (термопарами).
Трудоемкость подбора материалов конструкции (как правило, ракеты, спускаемые космические
аппараты и т.п.).
Трудоемкость проектирования и изготовления систем охлаждения (в основном для топлива).
Изготовление термически стабильных топлив с низким давлением насыщенных паров.
7

8.

Теплотехника ПНИПУ
Параметры торможения
Давление торможения удобнее всего искать с помощью температуры торможения и уравнения
процесса:
если известно полное давление,
отсюда можно найти скорость потока.
так как торможение мгновенное,
процесс адиабатный
!
Для определения скорости потока требуется: p, p*, T
НО термодинамическую температуру в потоке невозможно измерить
ТОГДА:
термодинамическую температуру заменяют температурой
торможения через уравнение адиабатного процесса.
Давление торможения и полное давление измеряют трубкой Пито.
Без модификаций применима только для
дозвуковых потоков.
(При сверхзвуке возникнут скачки уплотнения)
8

9.

Теплотехника ПНИПУ
Адиабатное истечение
Пусть есть большой резервуар с неподвижным газом внутри. Внутри
резервуара создано некоторое давление.
К резервуару приварен насадок, через который газ выходит в
атмосферу с некоторой скоростью.
Пусть истечение адиабатное
В выходном сечении то же давление и температура, что и
внутри резервуара
расширяем до давления среды и получим максимальное
значение при давлении среды, равном 0.
вся энтальпия превратится
в кинетическую энергию.
Можно вводить безразмерные
величины, тогда
Для неподвижного газа Λ = 0.
Для потока с максимальной скоростью Λ = 1.
9

10.

Теплотехника ПНИПУ
Скорость звука. Критическая скорость
Звуковые волны это
распространяющиеся в среде малые
изменения давления и плотности.
малые изменения
давления и плотности
Так как процесс изменения указанных
параметров происходит в пределах волны,
т.е. очень быстро, его можно считать
адиабатным. С учетом 1 закона ТД:
Формула Лапласа. Говорит о том, что чем горячее газ, тем он жестче, а
значит, выше скорость звука в нем.
показатель адиабаты можно
записать так…
число Маха
… а оценить скорость
потока можно так
10

11.

Теплотехника ПНИПУ
Скорость звука. Критическая скорость
НО! Если изменение давления и плотности среды
значительное, то, как правило, их скорость
превышает скорость звука.
В этом случае речь идет об ударных волнах.
В среде возникают скачки уплотнения – области
в движущемся потоке газа, в которых резко
возрастает давление, температура и плотность
при столь же резком падении скорости газа.
11

12.

Теплотехника ПНИПУ
Критическая скорость
Пусть поток энергетически изолирован, тогда:
Это ПОЛНАЯ энергия потока
Поток отсюда вылетает в
пространство, полностью
расширяясь.
Скорость потока падает по
мере расширения и прогрева
газа
1
Критическое состояние
потока: скорость потока равна
скорости звука в нем.
2
3
А скорость звука растет!
Критические параметры (давление и
температуру) можно отыскать через
первый закон термодинамики для
энергетически изолированного
потока.
12

13.

Теплотехника ПНИПУ
Критическая скорость
Разделили на температуру и заменили скорость
потока на критическую скорость звука.
При условии адиабатного истечения
Величина
критической
скорости
определяет
максимальный расход газа при истечении через
сужающееся сопло постоянной площадью выходного
сечения.
Скорость потока, как обычную, так и максимальную, можно сравнивать с критической скоростью
звука (аналог числа Маха). Эта безразмерная скорость обозначается буквой и называется
коэффициентом скорости.
13

14.

Теплотехника ПНИПУ
Уравнение обращения воздействий
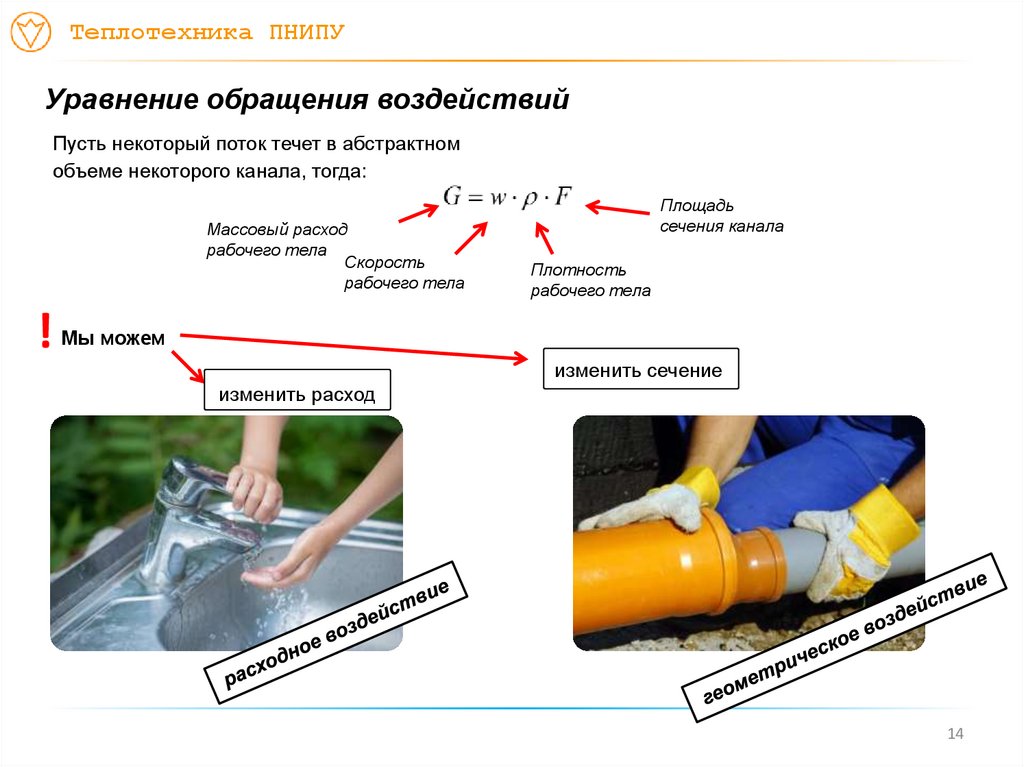
Пусть некоторый поток течет в абстрактном
объеме некоторого канала, тогда:
Массовый расход
рабочего тела
Скорость
рабочего тела
!
Площадь
сечения канала
Плотность
рабочего тела
Мы можем
изменить сечение
изменить расход
14

15.

Теплотехника ПНИПУ
Уравнение обращения воздействий
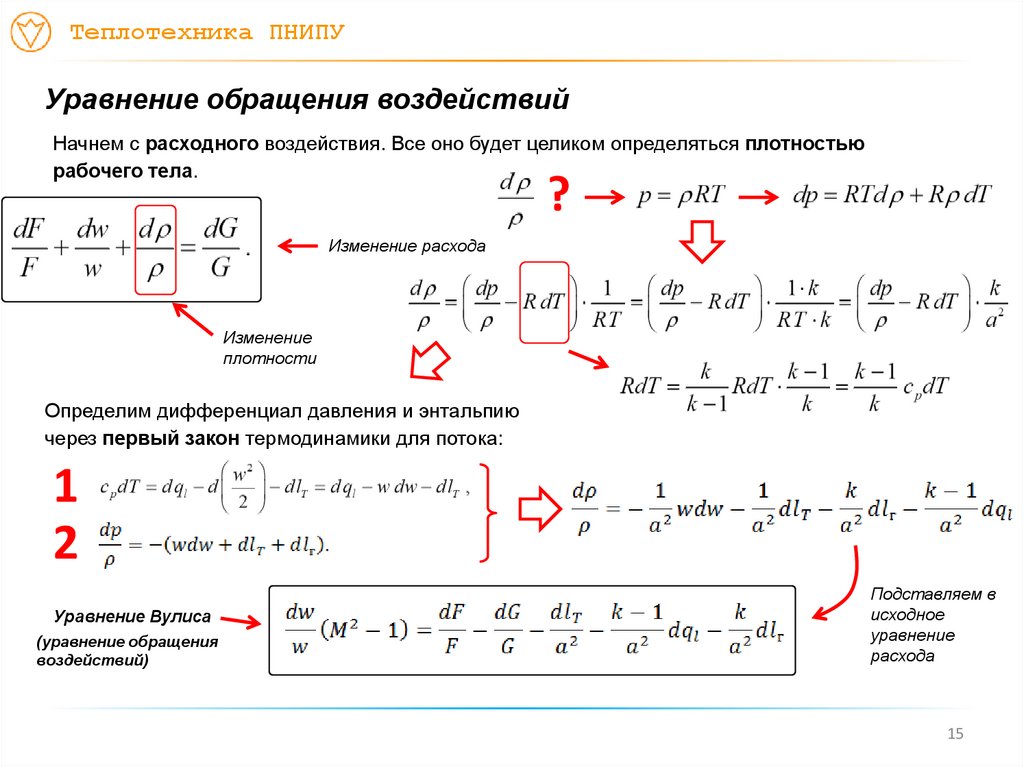
Начнем с расходного воздействия. Все оно будет целиком определяться плотностью
рабочего тела.
?
Изменение расхода
Изменение
плотности
Определим дифференциал давления и энтальпию
через первый закон термодинамики для потока:
1
2
Уравнение Вулиса
(уравнение обращения
воздействий)
Подставляем в
исходное
уравнение
расхода
15

16.

Теплотехника ПНИПУ
Уравнение обращения воздействий
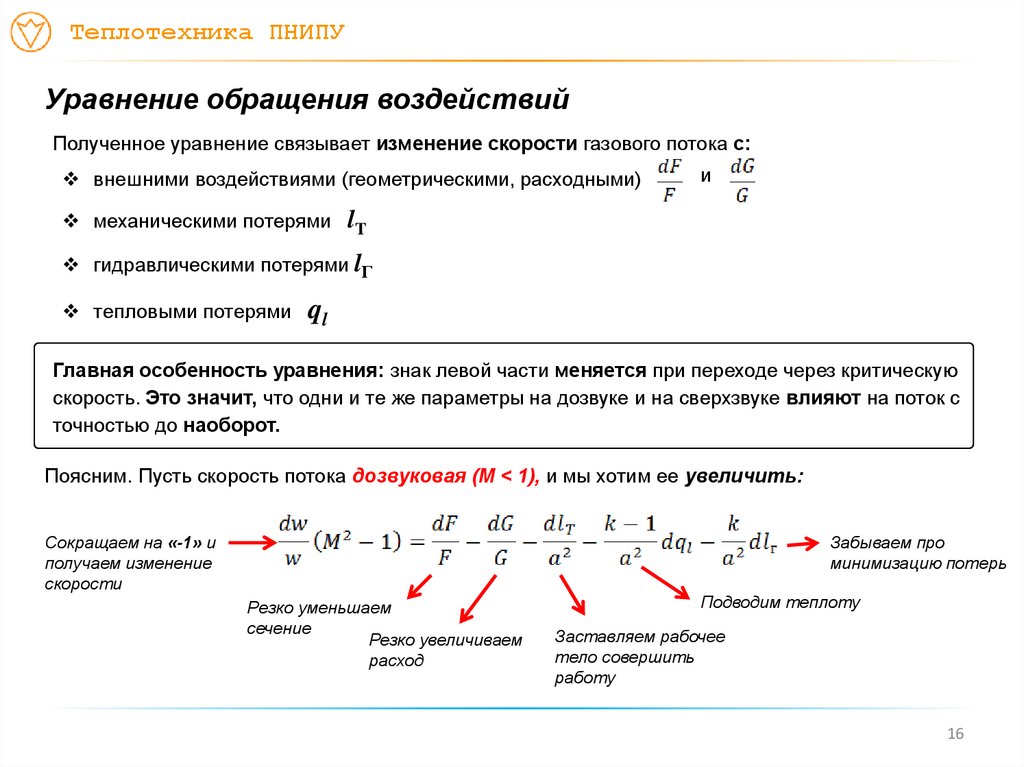
Полученное уравнение связывает изменение скорости газового потока с:
внешними воздействиями (геометрическими, расходными)
механическими потерями
и
lT
гидравлическими потерями lГ
тепловыми потерями
ql
Главная особенность уравнения: знак левой части меняется при переходе через критическую
скорость. Это значит, что одни и те же параметры на дозвуке и на сверхзвуке влияют на поток с
точностью до наоборот.
Поясним. Пусть скорость потока дозвуковая (M < 1), и мы хотим ее увеличить:
Сокращаем на «-1» и
получаем изменение
скорости
Забываем про
минимизацию потерь
Резко уменьшаем
сечение
Резко увеличиваем
расход
Подводим теплоту
Заставляем рабочее
тело совершить
работу
16

17.

Теплотехника ПНИПУ
Уравнение обращения воздействий
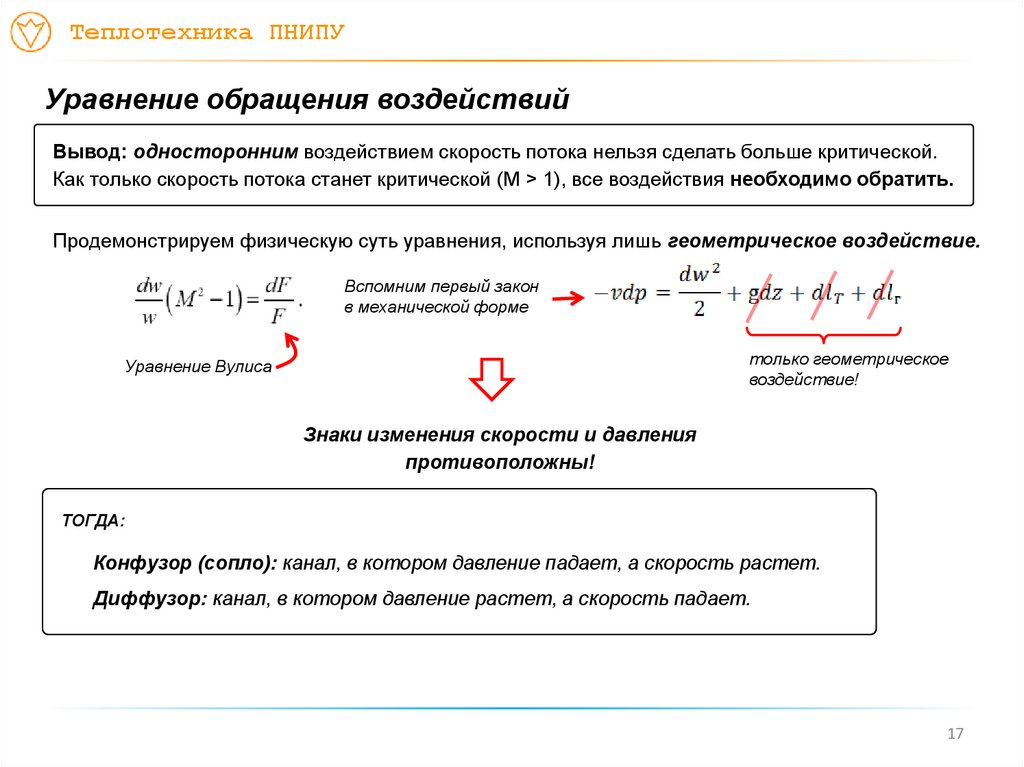
Вывод: односторонним воздействием скорость потока нельзя сделать больше критической.
Как только скорость потока станет критической (M > 1), все воздействия необходимо обратить.
Продемонстрируем физическую суть уравнения, используя лишь геометрическое воздействие.
Вспомним первый закон
в механической форме
только геометрическое
воздействие!
Уравнение Вулиса
Знаки изменения скорости и давления
противоположны!
ТОГДА:
Конфузор (сопло): канал, в котором давление падает, а скорость растет.
Диффузор: канал, в котором давление растет, а скорость падает.
17

18.

Теплотехника ПНИПУ
Уравнение обращения воздействий
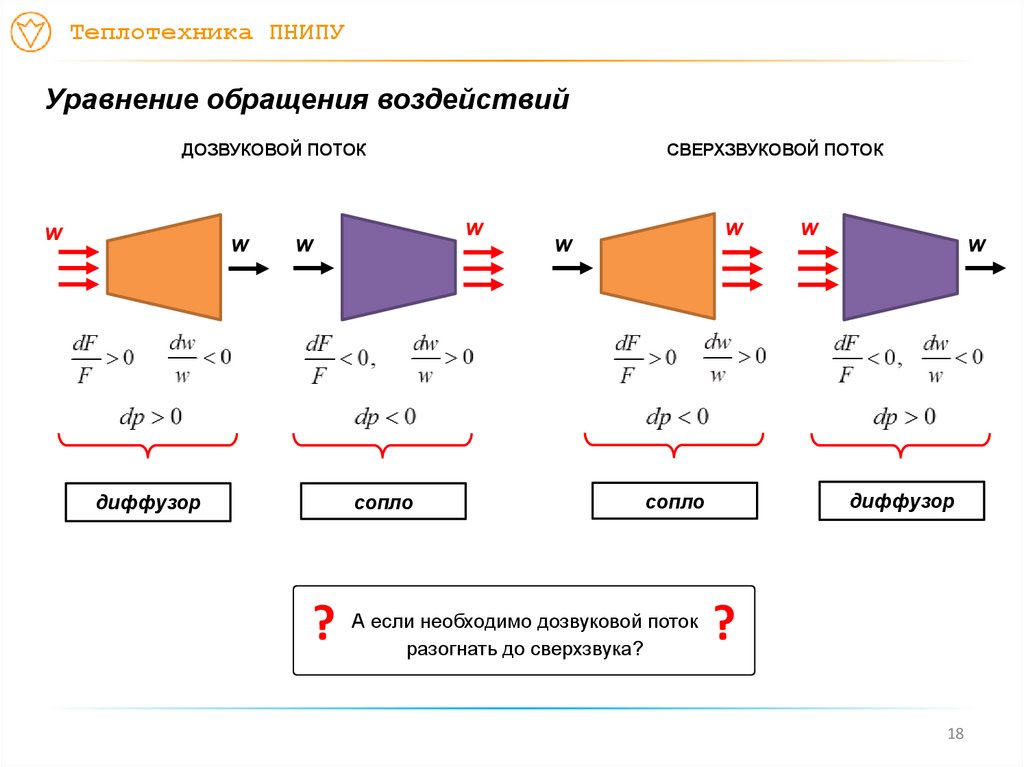
ДОЗВУКОВОЙ ПОТОК
w
w
w
w
диффузор
сопло
?
СВЕРХЗВУКОВОЙ ПОТОК
w
w
w
диффузор
сопло
А если необходимо дозвуковой поток
разогнать до сверхзвука?
w
?
18

19.

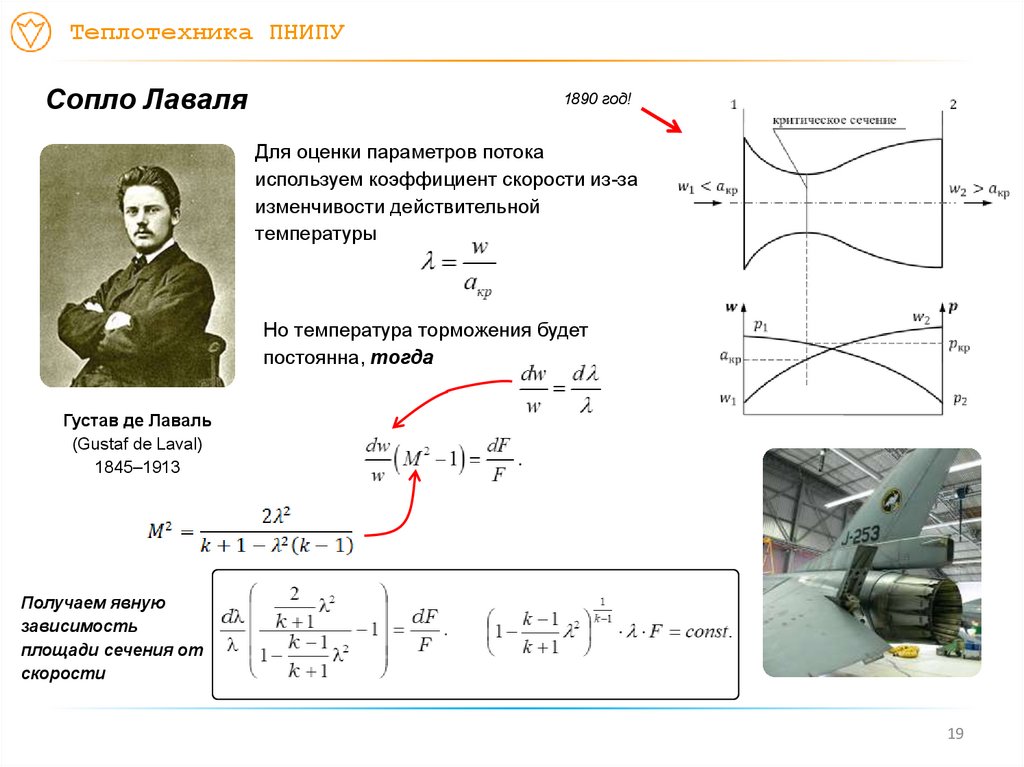
Теплотехника ПНИПУ
Сопло Лаваля
1890 год!
Для оценки параметров потока
используем коэффициент скорости из-за
изменчивости действительной
температуры
Но температура торможения будет
постоянна, тогда
Густав де Лаваль
(Gustaf de Laval)
1845–1913
Получаем явную
зависимость
площади сечения от
скорости
19

20.

Теплотехника ПНИПУ
Скачки уплотнения
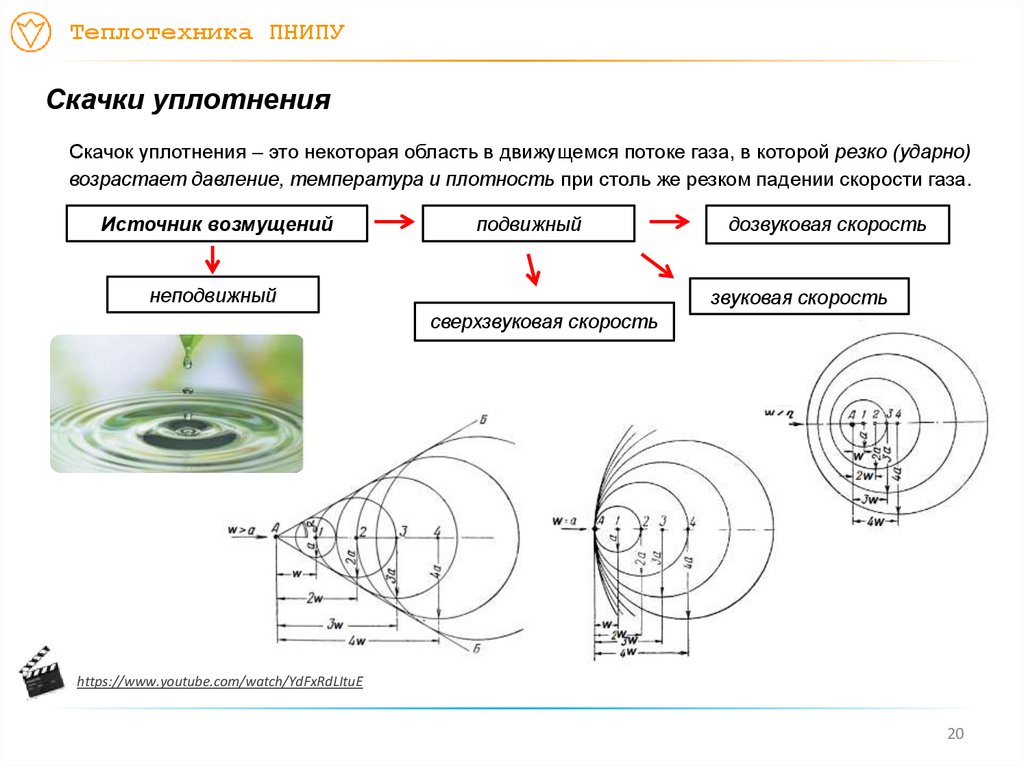
Скачок уплотнения – это некоторая область в движущемся потоке газа, в которой резко (ударно)
возрастает давление, температура и плотность при столь же резком падении скорости газа.
Источник возмущений
подвижный
неподвижный
дозвуковая скорость
звуковая скорость
сверхзвуковая скорость
https://www.youtube.com/watch/YdFxRdLItuE
20

21.

Теплотехника ПНИПУ
Скачки уплотнения
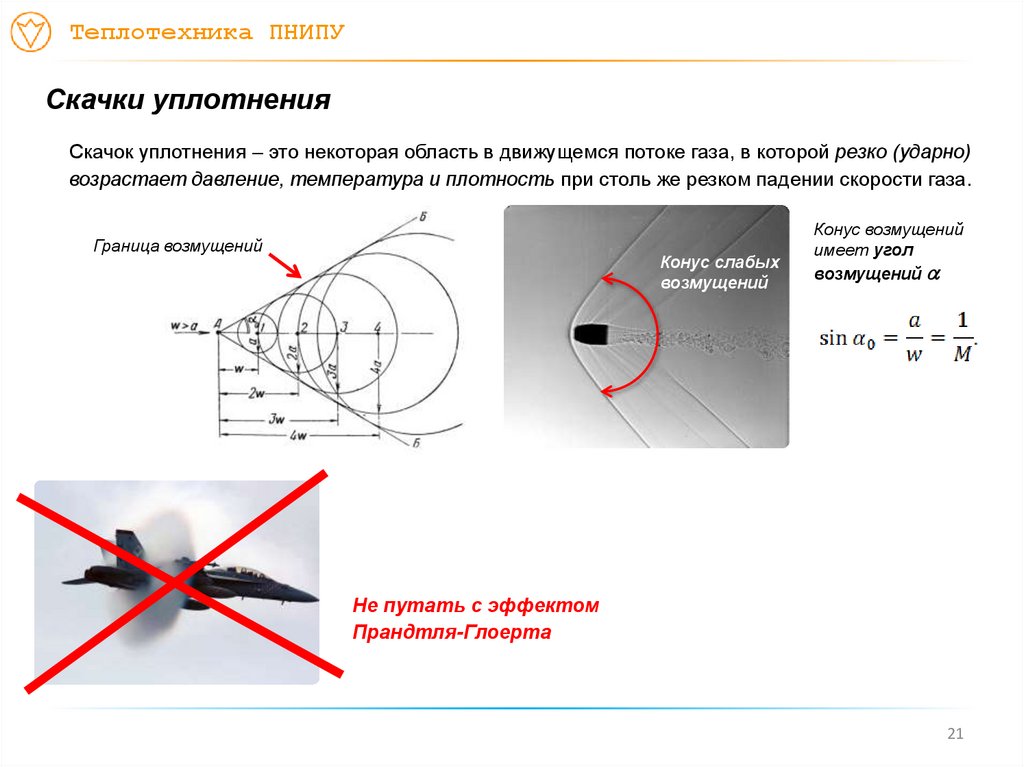
Скачок уплотнения – это некоторая область в движущемся потоке газа, в которой резко (ударно)
возрастает давление, температура и плотность при столь же резком падении скорости газа.
Граница возмущений
Конус слабых
возмущений
Конус возмущений
имеет угол
возмущений
Не путать с эффектом
Прандтля-Глоерта
21

22.

Теплотехника ПНИПУ
Скачки уплотнения
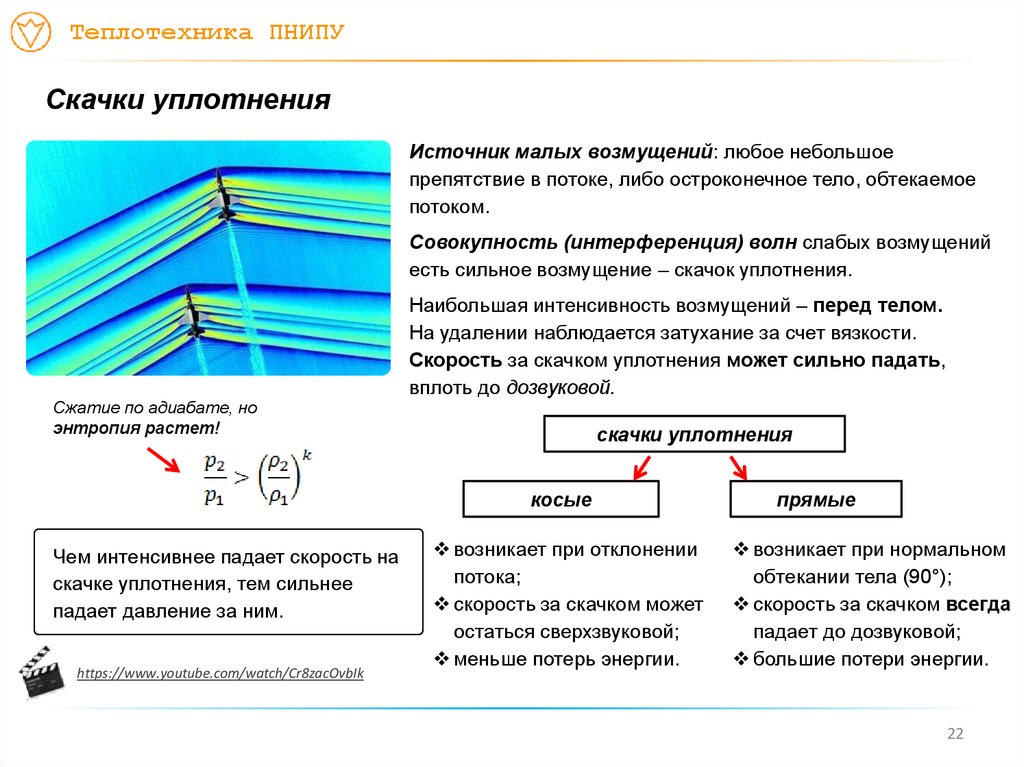
Источник малых возмущений: любое небольшое
препятствие в потоке, либо остроконечное тело, обтекаемое
потоком.
Совокупность (интерференция) волн слабых возмущений
есть сильное возмущение – скачок уплотнения.
Сжатие по адиабате, но
энтропия растет!
Наибольшая интенсивность возмущений – перед телом.
На удалении наблюдается затухание за счет вязкости.
Скорость за скачком уплотнения может сильно падать,
вплоть до дозвуковой.
скачки уплотнения
косые
Чем интенсивнее падает скорость на
скачке уплотнения, тем сильнее
падает давление за ним.
https://www.youtube.com/watch/Cr8zacOvbIk
возникает при отклонении
потока;
скорость за скачком может
остаться сверхзвуковой;
меньше потерь энергии.
прямые
возникает при нормальном
обтекании тела (90°);
скорость за скачком всегда
падает до дозвуковой;
большие потери энергии.
22

23.

Теплотехника ПНИПУ
Расчет скачков уплотнения. Прямой скачок
Для расчета необходимо:
После скачка
индекс 2
уравнение неразрывности;
уравнение количества движения;
первый закон термодинамики.
соблюдаем закон сохранения массы. Сколько
было перед скачком, столько станет и за ним
Найдем изменение количества движения по закону сохранения импульса:
Перед скачком
индекс 1
Импульс силы
Теперь исследуем изменение температуры, домножив уравнение для температуры торможения на
теплоемкость рабочего тела, записанную через k и R, заменим через скорость звука некоторые
величины:
делим на
, умножаем на
23

24.

Теплотехника ПНИПУ
Расчет скачков уплотнения. Прямой скачок
дозвук
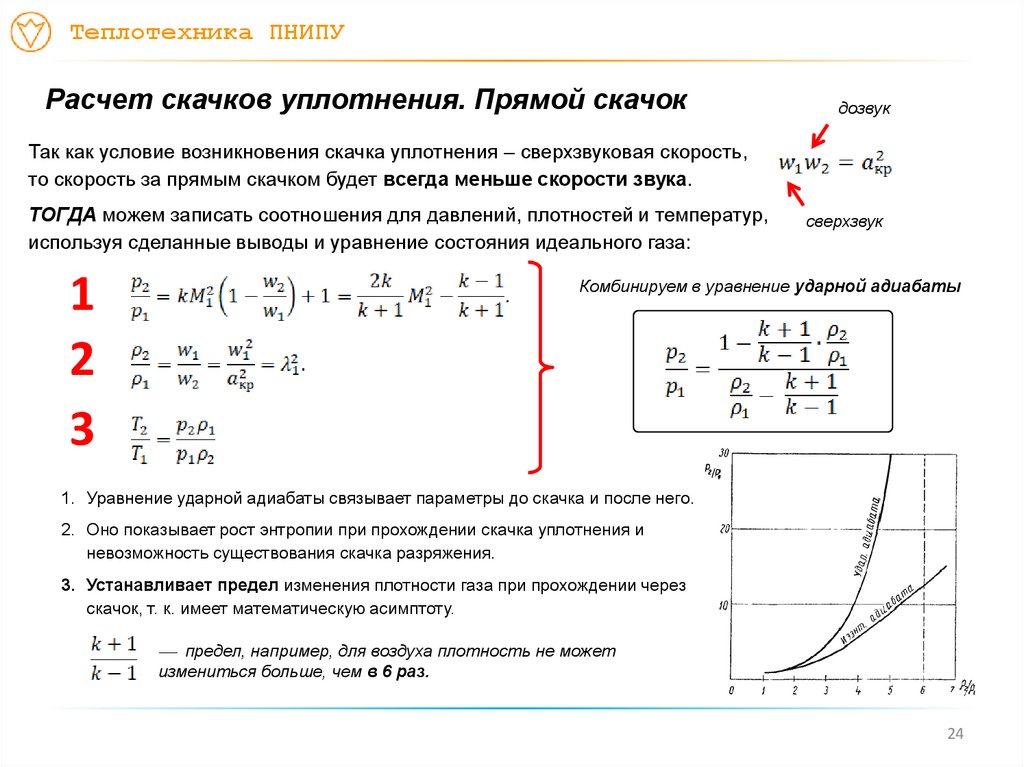
Так как условие возникновения скачка уплотнения – сверхзвуковая скорость,
то скорость за прямым скачком будет всегда меньше скорости звука.
ТОГДА можем записать соотношения для давлений, плотностей и температур,
используя сделанные выводы и уравнение состояния идеального газа:
1
2
3
сверхзвук
Комбинируем в уравнение ударной адиабаты
1. Уравнение ударной адиабаты связывает параметры до скачка и после него.
2. Оно показывает рост энтропии при прохождении скачка уплотнения и
невозможность существования скачка разряжения.
3. Устанавливает предел изменения плотности газа при прохождении через
скачок, т. к. имеет математическую асимптоту.
предел, например, для воздуха плотность не может
измениться больше, чем в 6 раз.
24

25.

Теплотехника ПНИПУ
Расчет скачков уплотнения. Прямой скачок
Таким образом, если для обычного адиабатного процесса изменение энтропии равно 0
выражение под логарифмом = 1
То при прохождении скачка уплотнения выражение под
логарифмом становится больше 1:
С учетом этого по первому закону термодинамики полное давление за скачком:
Будет меньше 1, т.к.
скорость меньше звуковой
25

26.

Теплотехника ПНИПУ
Расчет скачков уплотнения. Косой скачок
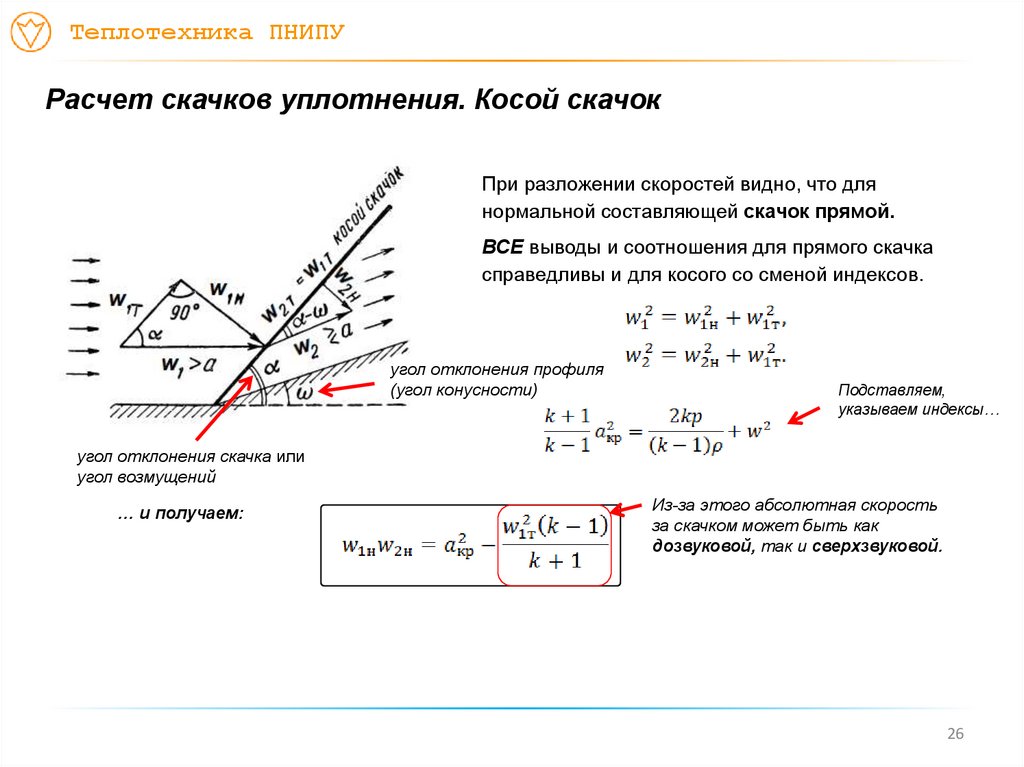
При разложении скоростей видно, что для
нормальной составляющей скачок прямой.
ВСЕ выводы и соотношения для прямого скачка
справедливы и для косого со сменой индексов.
угол отклонения профиля
(угол конусности)
Подставляем,
указываем индексы…
угол отклонения скачка или
угол возмущений
… и получаем:
Из-за этого абсолютная скорость
за скачком может быть как
дозвуковой, так и сверхзвуковой.
26

27.

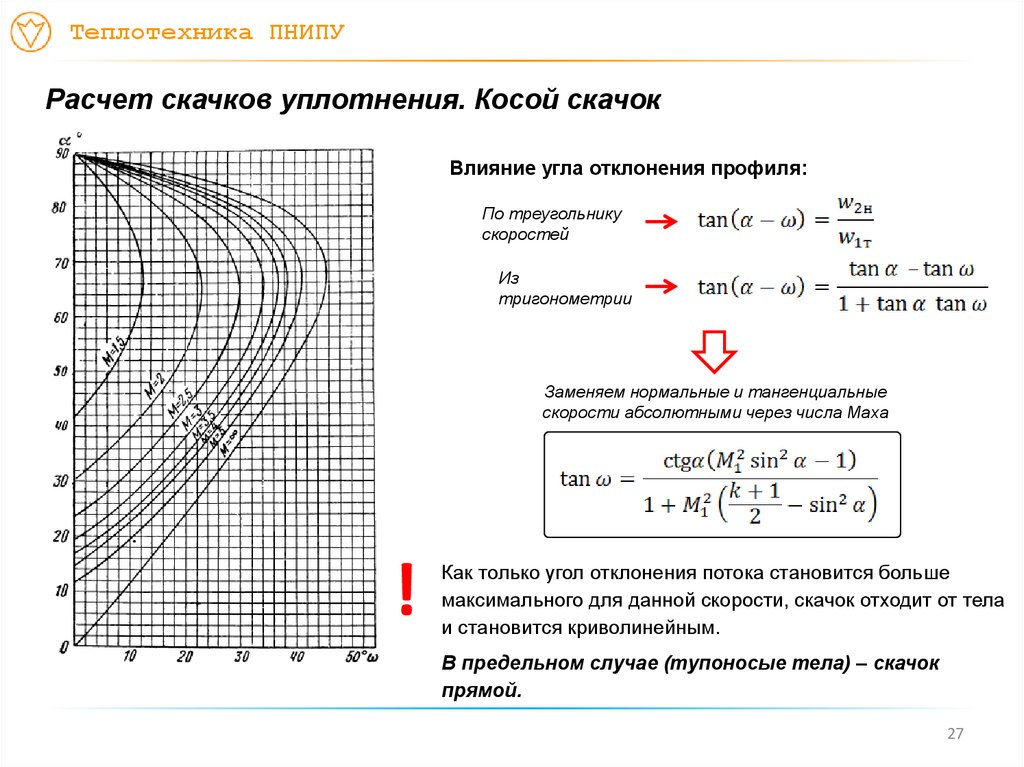
Теплотехника ПНИПУ
Расчет скачков уплотнения. Косой скачок
Влияние угла отклонения профиля:
По треугольнику
скоростей
Из
тригонометрии
Заменяем нормальные и тангенциальные
скорости абсолютными через числа Маха
!
Как только угол отклонения потока становится больше
максимального для данной скорости, скачок отходит от тела
и становится криволинейным.
В предельном случае (тупоносые тела) – скачок
прямой.
27

28.

Теплотехника ПНИПУ
В общем-то, всё!
Теплотехника ПНИПУ
Секция теплотехники каф. СПМиТМ
Механико-технологический факультет ПНИПУ
614990 г. Пермь, ул. Комсомольский проспект 29, ауд. 013, к. А.,
тел. 2198-175, e-mail: [email protected]
© 2002-2023 WebMaster [email protected]
28