Физические состояния полимеров. Термомеханическая кривая

1.

Физические состояния полимеров

2.

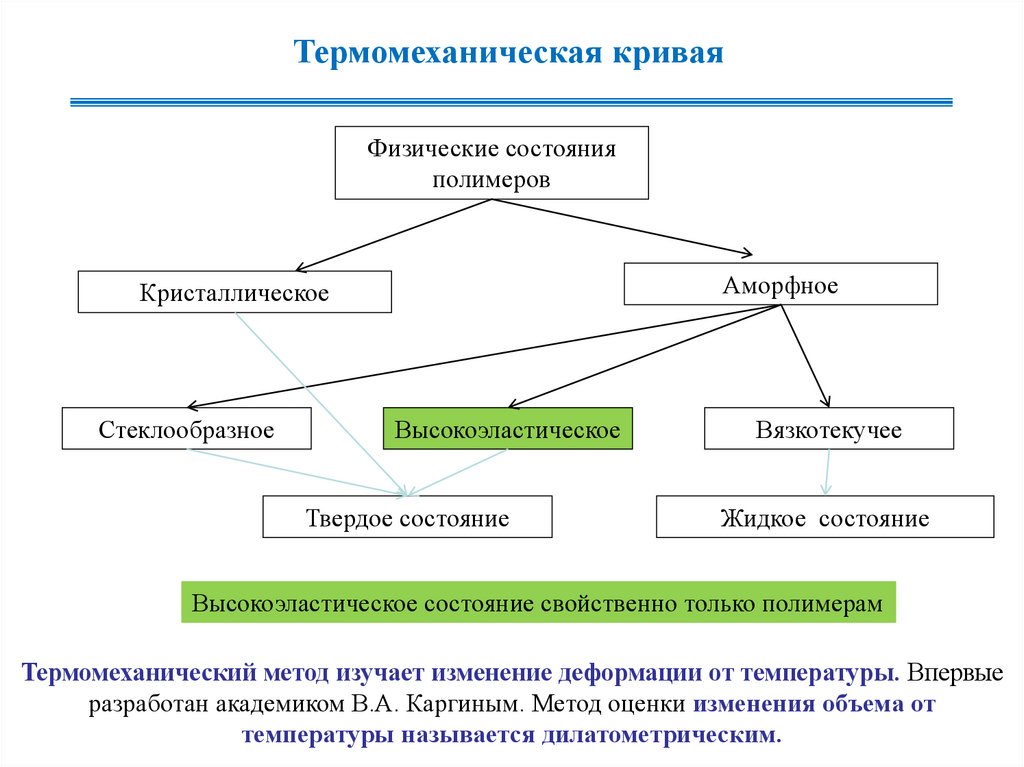
Термомеханическая кривая
Физические состояния
полимеров
Аморфное
Кристаллическое
Стеклообразное
Высокоэластическое
Твердое состояние
Вязкотекучее
Жидкое состояние
Высокоэластическое состояние свойственно только полимерам
Термомеханический метод изучает изменение деформации от температуры. Впервые
разработан академиком В.А. Каргиным. Метод оценки изменения объема от
температуры называется дилатометрическим.

3.

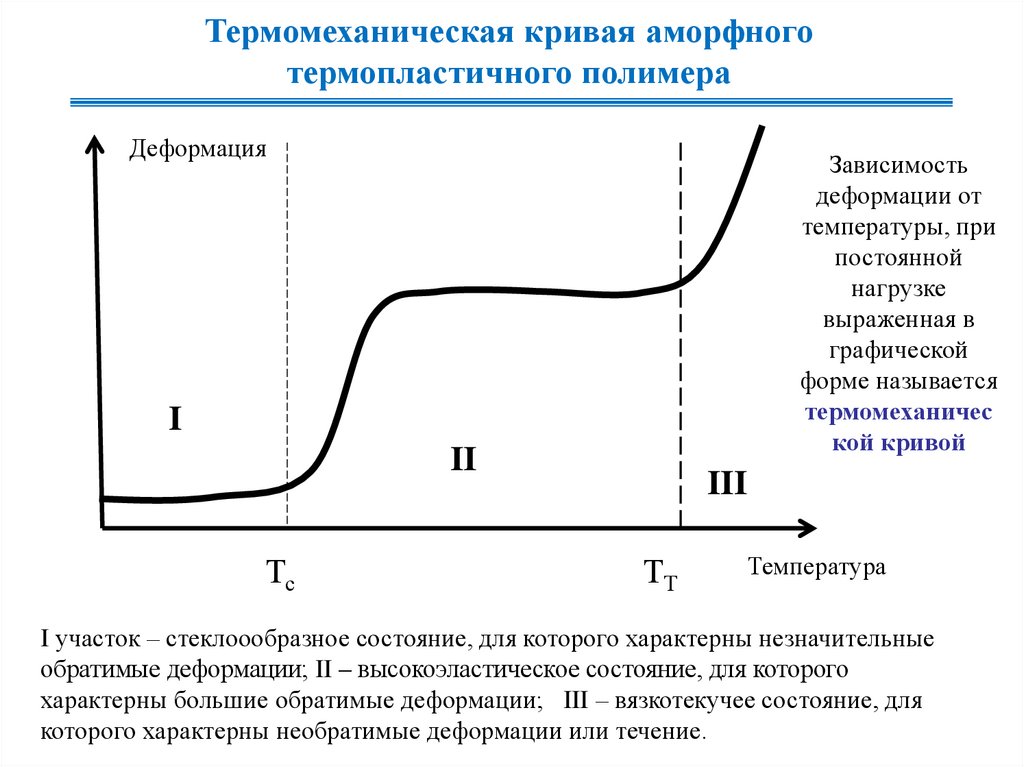
Термомеханическая кривая аморфного
термопластичного полимера
Деформация
Зависимость
деформации от
температуры, при
постоянной
нагрузке
выраженная в
графической
форме называется
термомеханичес
кой кривой
I
II
Тс
III
ТТ
Температура
I участок – стеклоообразное состояние, для которого характерны незначительные
обратимые деформации; II – высокоэластическое состояние, для которого
характерны большие обратимые деформации; III – вязкотекучее состояние, для
которого характерны необратимые деформации или течение.

4.

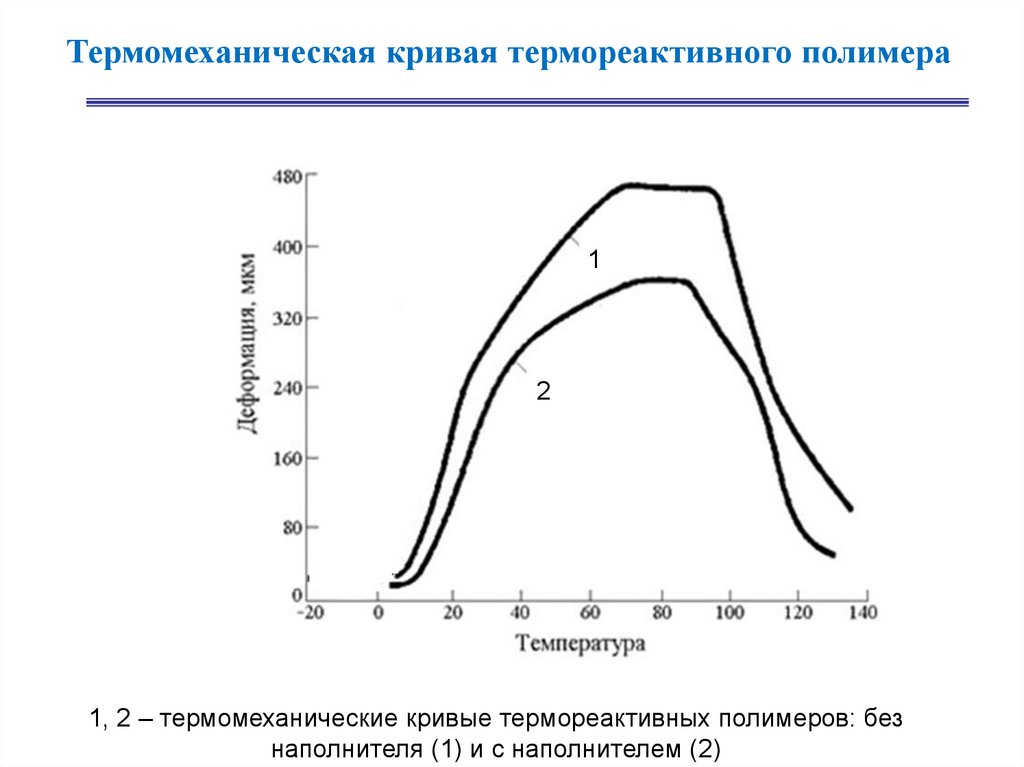
Термомеханическая кривая термореактивного полимера
1
2
1, 2 – термомеханические кривые термореактивных полимеров: без
наполнителя (1) и с наполнителем (2)

5.

Температура стеклования
Для стеклообразного состояния характерны:
- небольшие упругие деформации (<10%);
- высокие значения модуля упругости 2 103 - 5 104 МПа.
В стеклообразном состоянии полимеры деформируются как твердые тела.
Деформация осуществляется за счет изменения средних межатомных и
межмолекулярных расстояний (перемещением сегментов макромолекул,
содержащих 5 – 20 атомов основной цепи). Возможность деформации
полимера связана с существованием свободного объема, не занятого
макромолекулами. В застеклованном состоянии полимер обладает наименьшим
свободным объемом, величина которого мало зависит от типа полимера и
составляет несколько процентов. По мере повышения температуры величина
свободного объема возрастает.
Выше температуры стеклования начинает изменяться жесткость
макромолекул, что приводит к снижению прочности и жесткости полимера.
5

6.

Релаксационные переходы при температуре стеклования
В зависимости от температуры, имеют место
различные пики релаксации, обычно называемые γ, β
и α. Все они связаны с молекулярной подвижностью,
амплитуды которых возрастают с повышением
температуры.
При низкой температуре (γ-пик), имеет место
вращения радикалов.
При средней температуре (β –пик) возникает
подвижность отдельных участков цепи.
При при высокой температуре (α-пик) изменяется
температура стеклования, связанная с подвижностью
развернутых участков цепей между узлами на
большом расстоянии.
При температуре T > Tс для полимера характерен большое конформационный набор и
большая конформационная энтропия. С уменьшением температуры снижается
гибкость цепи и поэтому большие конформации «вымораживаются». Температура, при
которой фазовое движение сегментов макромолекулы полностью прекращается
называют температурой фазового перехода второго рода T2 .
На практике всегда T с > T2 , но при бесконечно малых скоростях охлаждения условно
6
предполагают, что T с = T2

7.

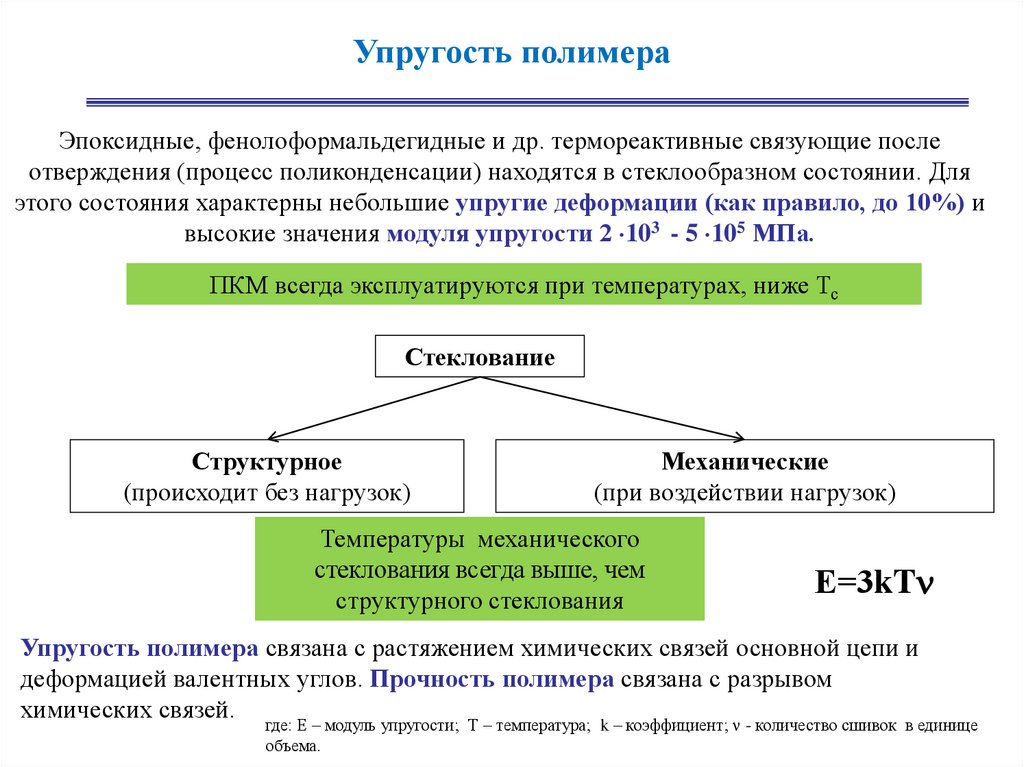
Упругость полимера
Эпоксидные, фенолоформальдегидные и др. термореактивные связующие после
отверждения (процесс поликонденсации) находятся в стеклообразном состоянии. Для
этого состояния характерны небольшие упругие деформации (как правило, до 10%) и
высокие значения модуля упругости 2 103 - 5 105 МПа.
ПКМ всегда эксплуатируются при температурах, ниже Тс
Стеклование
Структурное
(происходит без нагрузок)
Механические
(при воздействии нагрузок)
Температуры механического
стеклования всегда выше, чем
структурного стеклования
Е=3kT
Упругость полимера связана с растяжением химических связей основной цепи и
деформацией валентных углов. Прочность полимера связана с разрывом
химических связей. где: Е – модуль упругости; Т – температура; k – коэффициент; - количество сшивок в единице
объема.

8.

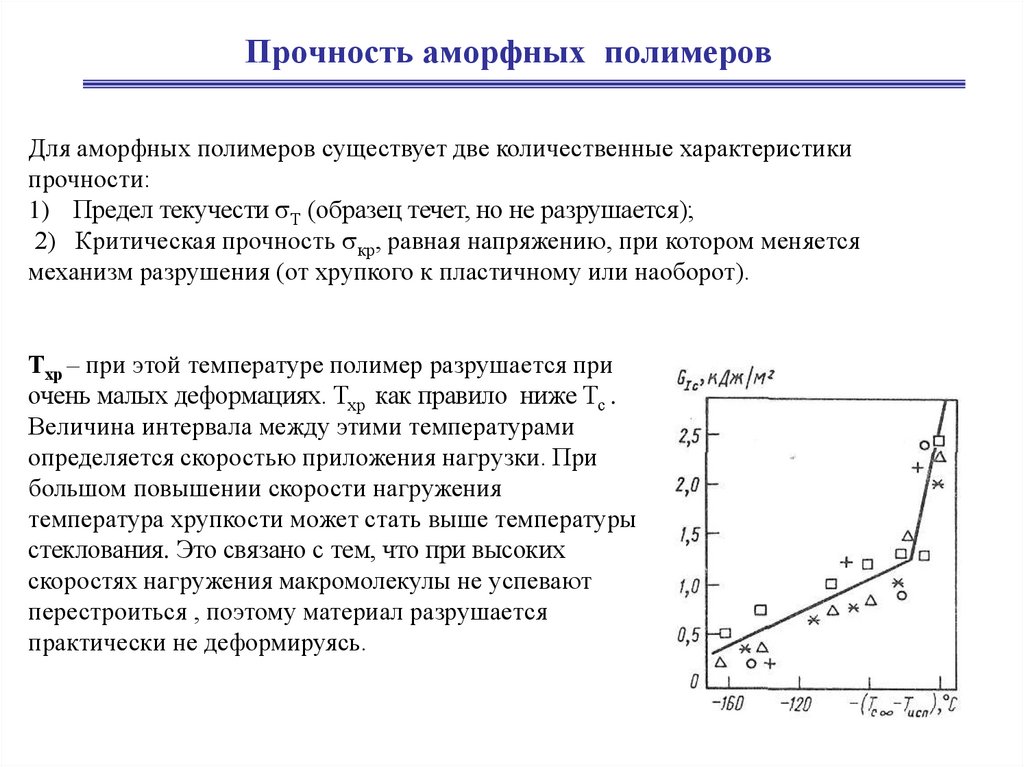
Прочность аморфных полимеров
Для аморфных полимеров существует две количественные характеристики
прочности:
1) Предел текучести Т (образец течет, но не разрушается);
2) Критическая прочность кр, равная напряжению, при котором меняется
механизм разрушения (от хрупкого к пластичному или наоборот).
Тхр – при этой температуре полимер разрушается при
очень малых деформациях. Тхр как правило ниже Тс .
Величина интервала между этими температурами
определяется скоростью приложения нагрузки. При
большом повышении скорости нагружения
температура хрупкости может стать выше температуры
стеклования. Это связано с тем, что при высоких
скоростях нагружения макромолекулы не успевают
перестроиться , поэтому материал разрушается
практически не деформируясь.

9.

Высокоэластическое состояние
II.
I
II
III
Это область характеризуется относительно высокой
подвижностью сегментов макромолекул.
Высокоэластическое состояние присуще только
полимерным материалам, так как вследствие гибкости
макромолекул возможно изменение их формы и
перемещение отдельных частей макромолекул без
смещения их в целом относительно друг друга.
Тg
Под релаксационными явлениями понимают изменение свойств полимеров во
времени, обусловленное достижением равновесного состояния. В основе
релаксационных явлений лежит вязкоупругость.
Временем релаксации также называют время необходимое для перестройки структуры
системы, подвергающейся воздействию, от равновестного состояния в неравновестное.
Важнейшие вязкоупругие свойства полимеров:
- при статическом нагружении имеет место ползучесть и релаксация напряжений;
- при динамических нагрузках (или динамических деформациях) имеет место
отставание деформации от напряжения (или наоборот).

10.

Природа вязкоупругости полимеров
n3
где – время релаксации; n – число звеньев между двумя
сшивками. (т.е. для полимеров время релаксации в n3
больше по сравнению с низкомолекулярными жидкостями.
Для гибкоцепных молекул 500 > n > 50, что приблизительно соответствует
молекулярной массе
105 > M > 104
Вязкоупругость проявляется только в том случае, если время t воздействия на
полимер соизмеримо со временем релаксации .
При > t проявляться упругие свойства.
При < t проявляются вязкие свойства (течение).
При n = 104 время релаксации может измеряться как в секундах, так и в минутах и даже часах.
Время релаксации – макроскопическая величина. С увеличением количества водородных
связей или сил Ван-дер-Ваальсового взаимодействия, время релаксации увеличивается.

11.

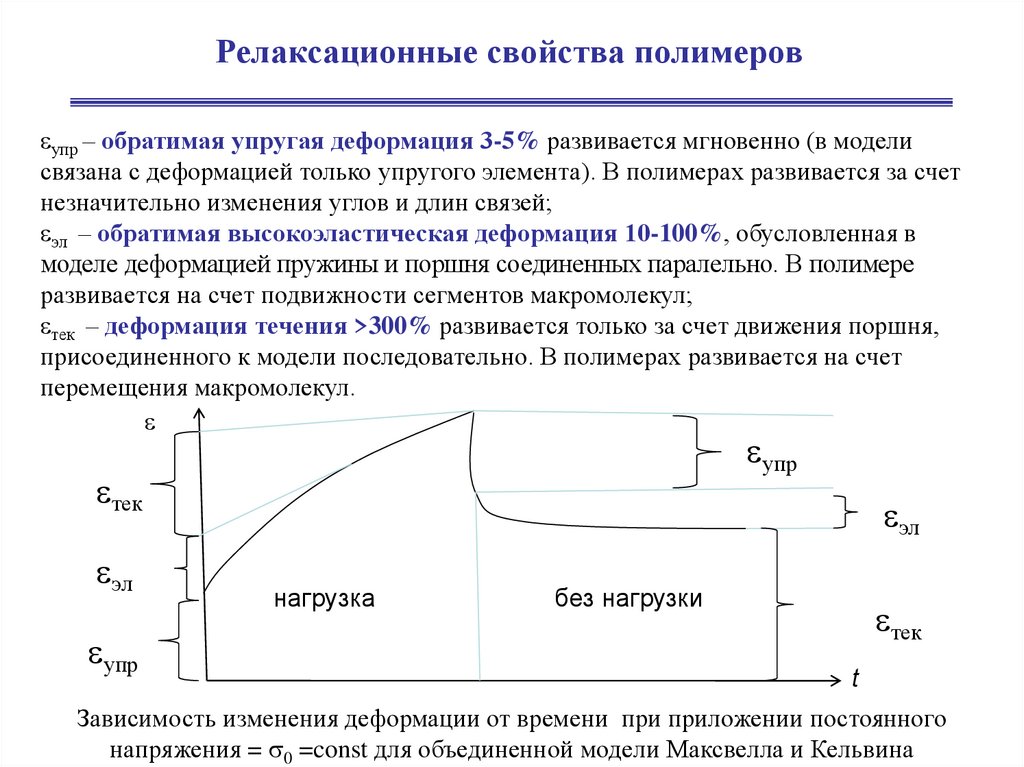
Релаксационные свойства полимеров
упр – обратимая упругая деформация 3-5% развивается мгновенно (в модели
связана с деформацией только упругого элемента). В полимерах развивается за счет
незначительно изменения углов и длин связей;
эл – обратимая высокоэластическая деформация 10-100%, обусловленная в
моделе деформацией пружины и поршня соединенных паралельно. В полимере
развивается на счет подвижности сегментов макромолекул;
тек – деформация течения >300% развивается только за счет движения поршня,
присоединенного к модели последовательно. В полимерах развивается на счет
перемещения макромолекул.
упр
тек
эл
упр
эл
нагрузка
без нагрузки
тек
t
Зависимость изменения деформации от времени при приложении постоянного
напряжения = 0 =const для объединенной модели Максвелла и Кельвина

12.

Упругий гистерезис полимеров
Растяжение
Сжатие
Необратимая деформация
= 0 sin wt
w = 2 /v
= 0 (sin wt - )
Несовпадение зависимостей
отвечающих растяжению и
сжатию свидетельствует о потере
части упругой энергии которая
превращается в тепло и
необратимо рассеивается в
результате трения, возникающего
при перемещении сегментов
макромолекул. В результате
постепенно идет накопление
необратимой деформации.
где w – круговая частота, связанная с периодом колебаний; v – период колебаний;
0 - амплитудной значение напряжений; t – время; - угол сдвига фаз (он связан с
так называемыми механическими потерями, которые представляют собой долю
упругой энергии, превращенную в тепло).
Петля Гистерезиса соответствует только одному циклу нагружений. При каждом
последующем цикле ее форма немного видоизменяется. При тепловом режиме петля
приобретает форму элипса и остается неизменной.

13.

Природа вязкоупругости полимеров
Особенностью полимеров является то, что они одновременно обладают свойствами
твердого (упругого) тела и жидкости. Это общее для всех полимеров явление
называется вязкоупругостью.
Уравнение Ньютона-Стокса
=
- напряжение сдвига; - скоростью сдвига; - вязкость.
(t) = 0 exp (-t/ )
- время релаксации, т.е. это время в течение которого напряжение уменьшается
в «е» раз.
Уменьшение напряжений при фиксированной деформации упруговязкого тела
называется релаксацией напряжений.

14.

Принцип температурно-временной суперпозиции
Этот принцип разработан Вильямсом, Ланделом и Ферри. Он является
универсальным по отношению ко всем полимерным материалам.
Глубина релаксации определяется только двумя факторами: вренем и
температурой и их влияние эквивалентно.
Эквивалентность факторов времени и температуры позволяет осуществлять
взаимный пересчет вязкоупругих характеристик полимера. Такой подход
получил название принцип температурно-временной суперпозиции.
= В exp(Eo / kT)
где - время релаксации; В, k – константs для данного полимера, зависящие от
объема структурного элемента; Т – температура; Eo - энергия активации.

15.

Вязко-текучее состояние
I
III.
II
III
ТТ
В области высоких температур тепловая
энергия достаточно велика и структура полимера
с изменением температуры успевает переходить в
новое состояние при изменении внешних условий.
Кинетические элементы структуры (отдельные
сегменты, группы или атомы), участвующие в
движении и обладающие большой тепловой
энергией, легко преодолевают энергетические
барьеры , которые препятствуют любым
изменениям структуры полимеры. К таким
барьерам относятся, например, межмолекулярное
взаимодействие и объемные препятствия,
связанные с близостью окружающих
макромолекул.

16.

Законы капиллярного течения
( ) ( )
Основной закон вискозиметрии (закон трения Ньютона)
Сдвиговое напряжение в твердом теле пропорционально
деформации, а в жидкости – скорости сдвига, т.е.
параметры G и служат одной и той же цели – это
коэффициент сопротивления, учитывающий природу тела,
подвергаемого сдвигу.
Чистый сдвиг
S
d
f
( )
S
Напряжением сдвига ( ) называют
отношение приложенной силы (это сила
трения) к единице площади.
Динамическая вязкость не учитывает прочность
структуры, но отражает скорость ее разрушения.
( )
v
d
Скорость сдвига ( )– это градиент
скорости в направлении перпендикулярном
приложенной силе.
Слой жидкости, толщиной d помещен между двумя плоскопараллельными пластинами, из которых одна, с
площадью S является подвижной. К подвижной пластине приложена сила f, под действием которой она
движется со скоростью v. Напряжение сдвига вызывает послойное разделение жидкости. Максимальная
16
скорость течения наблюдается у границы раздела жидкости с движущейся плоскостью.

17.

Кинематическая вязкость
мм 2
1 санти Стокс
с
3…6 мм
Материал (связующее)
Вязкость, при 20 С
Кинематическая ВЗ 2, м2/с
при 20 С
Вода
Бензин
Кровь
Эпоксидное
1,0035
0,1
100
400 - 2000
Число (критерий) Рейнольдса
Re – есть мера отношения сил
V D
инерции, действующих в потоке,
Re
к вязкости или это отношение
кинетической энергии жидкости к
потерям энергии на характерной
длине (ввиду внутреннего
V – скорость, м/с; - кинематическая
трения).
вязкость, Па с; D – гидравлический
диаметр, м.
17

18.

Динамическая вязкость (динамический коэффициент вязкости)
М
Н
2
м
1 Па с 1 сантипуаз
с
Реометр СAP 2000+
Реометр «RheoStress
6000»
Приборы, которые измеряют вязкоупругие характеристики,
называют реометрами. Приборы, которые определяют только
18
вязкость – вискозиметрами.

19.

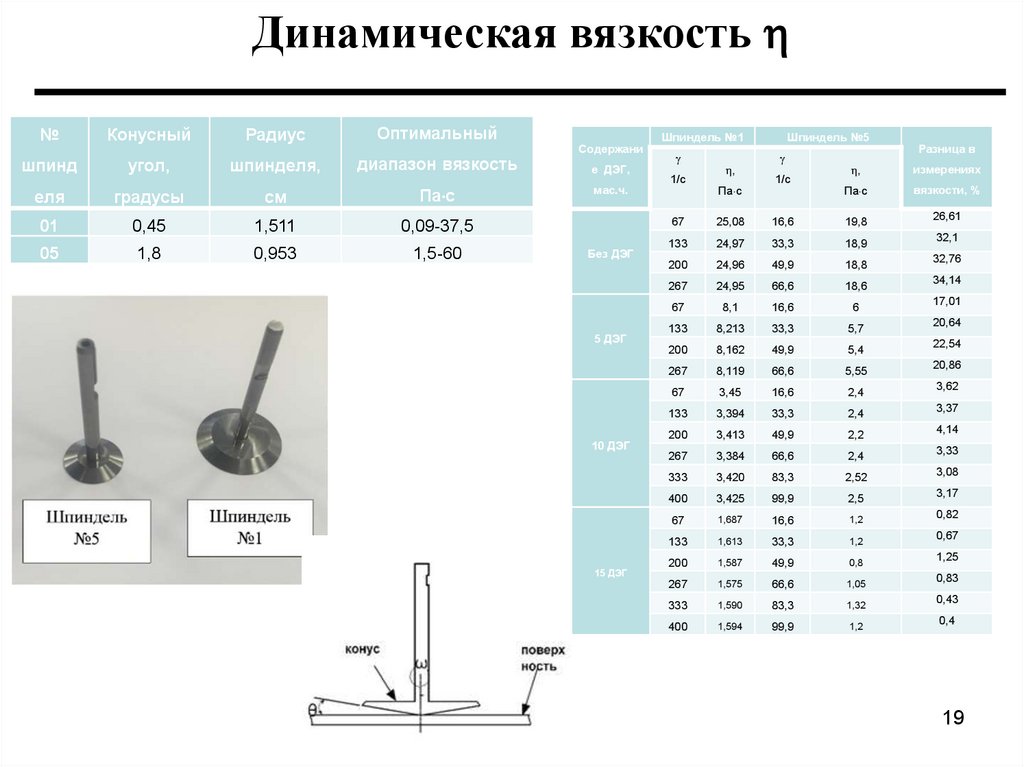
Динамическая вязкость
№
Конусный
Радиус
Оптимальный
шпинд
угол,
шпинделя,
диапазон вязкость
еля
градусы
см
Па с
01
0,45
1,511
0,09-37,5
05
1,8
0,953
1,5-60
Содержани
е ДЭГ,
мас.ч.
Без ДЭГ
5 ДЭГ
10 ДЭГ
15 ДЭГ
Шпиндель №1
1/с
,
Па с
Шпиндель №5
1/с
Разница в
,
измерениях
Па с
вязкости, %
26,61
67
25,08
16,6
19,8
133
24,97
33,3
18,9
200
24,96
49,9
18,8
267
24,95
66,6
18,6
67
8,1
16,6
6
133
8,213
33,3
5,7
200
8,162
49,9
5,4
267
8,119
66,6
5,55
67
3,45
16,6
2,4
133
3,394
33,3
2,4
200
3,413
49,9
2,2
267
3,384
66,6
2,4
333
3,420
83,3
2,52
400
3,425
99,9
2,5
67
1,687
16,6
1,2
0,82
133
1,613
33,3
1,2
0,67
200
1,587
49,9
0,8
1,25
267
1,575
66,6
1,05
0,83
333
1,590
83,3
1,32
0,43
400
1,594
99,9
1,2
0,4
32,1
32,76
34,14
17,01
20,64
22,54
20,86
3,62
3,37
4,14
3,33
3,08
3,17
19

20.

Кривые течения и вязкости
1 – ньютоновские (идеальные жидкости) в них отсутствует касательные силы, т.е. около твердых
поверхностей такие жидкости скользят (а не прилипают, как неноьютоновские жидкости);
2 – псевдопластичные (полимерные связующие для которых справедливо, чем выше скорость их смешения
или подачи, тем ниже их вязкость); При данной силе (давлении) воздействия большая масса материала может
быть переведена в текущее состояние, т.е. снижены затраты на поддержание течения за заданном уровне; Этот
эффект является обратимым, т.е. при снижении скорости сдвига высокие значения вязкости восстанавливаются.
3 – дилатантные жидкости.
20

21.

Вязкотекучее состояние полимера
Для термопластов – это расплав. Для реактопластов – это состояние олигомера до
начала его гелеобразования.
Течение термопластов – направленная диффузия сегментов макромолекул. Для
обеспечения течения необходимо два условия:
1) наличие тепловой энергии;
2) наличие микропустот (свободного объема) в который и осуществляется
перемещение сегмента.
Эффект Вайссенберга - это возникновение
нормальных напряжений, направленных
перпендикулярно приложенным сдвиговым
напряжением.
Эффект Вайссенберга имеет место вследствие того, что при
сдвиговой деформации клубки макромолекул деформируются ,
но тепловое движение сегментов стремиться вернуть их к
первоначальной конформации. В результате возникает
напряжение, перпендикулярное сдвиговому, которое и
заставляет «ползти» жидкость к верху по валу.

22.

Основные понятия реологии
Первоначально термин «реология» относился только к текучим системам. Термин «реология»
происходит от греческого глагола «рэо» - течь.
Сейчас реология трактуется как наука о законах деформации различных материалов, в том
числе и таких, для которых течение не является определяющим.
Предметом реологии является описание механических свойств материалов при различных
режимах деформирования, когда одновременно проявляется их способность к течению и
накоплению обратимых деформаций.
Реологические уравнения – это уравнения, устанавливающие связь между напряженным
состоянием среды, деформациями и скоростями деформации.
1. Аномалия вязкости при сдвиговом течении;
2. Возможность больших обратимых деформаций;
3. Вязкоупругая реакция на внешние воздействия (релаксация).
Эти три особенности свойств полимеров приводят к тому, что их рассматривают как нелинейные
вязкоупругие среды

23.

Реологические модели
1-я аксиома реологии:
Все материальные тела при всестороннем равномерном (изотропном) сжатии
ведут себя как идеальные упругие тела.
2-я аксиома реологии:
Любая материальная система обладает всеми реологическими свойствами
(упругостью, пластичностью, вязкостью, прочностью). Все эти свойства
проявляются при сдвиговой деформации-наиболее важной в реологии.
В реологии механические свойства материалов представляют в виде реологических моделей, в
основе которых лежат три основных идеальных закона, связывающих напряжение с деформацией.
Им соответствуют три модели идеальных материалов, отвечающих основным реологическим
характеристикам:
упругости,
пластичности
вязкости.
W- упругий потенциал, который характеризует упругую энергию, которая в
материале накапливается. D – интенсивность диссипации (рассеивание)
энергии в единице объема.
При условии W 0; D=0 – такая среда называется упругой.
При условии D 0; W=0 – такая среда называется вязкой.
При условии D 0; W 0 – такая среда называется вязкоупругой.
23

24.

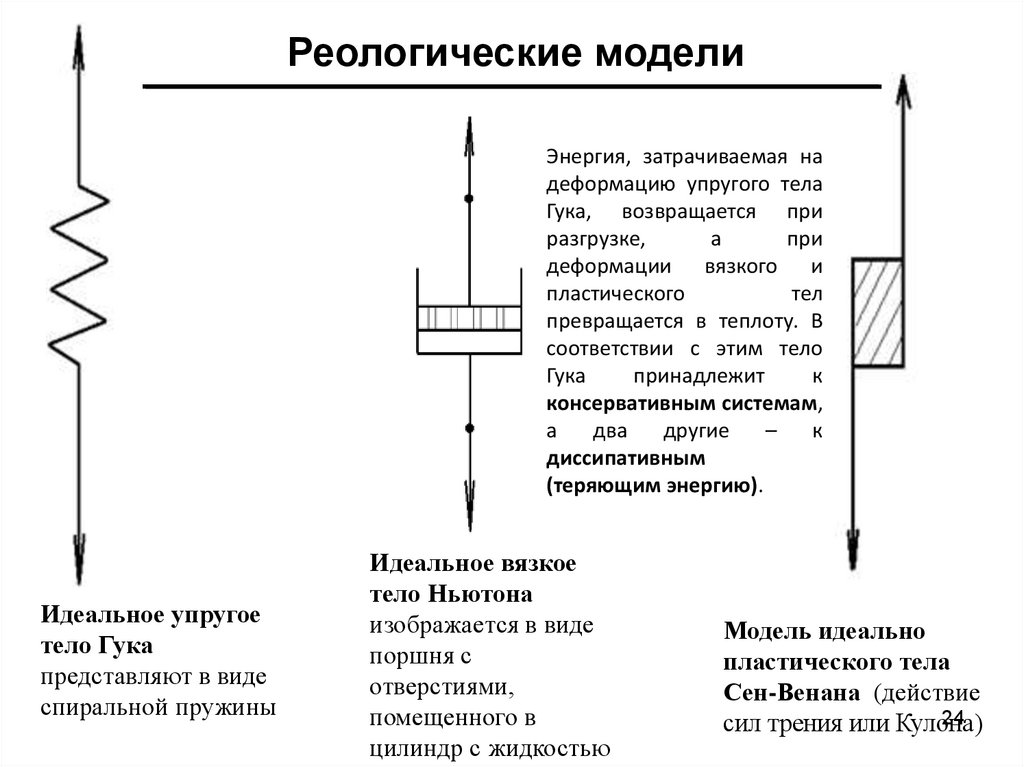
Реологические модели
Энергия, затрачиваемая на
деформацию упругого тела
Гука, возвращается при
разгрузке,
а
при
деформации вязкого и
пластического
тел
превращается в теплоту. В
соответствии с этим тело
Гука
принадлежит
к
консервативным системам,
а
два
другие
–
к
диссипативным
(теряющим энергию).
Идеальное упругое
тело Гука
представляют в виде
спиральной пружины
Идеальное вязкое
тело Ньютона
изображается в виде
поршня с
отверстиями,
помещенного в
цилиндр с жидкостью
Модель идеально
пластического тела
Сен-Венана (действие
24
сил трения или Кулона)

25.

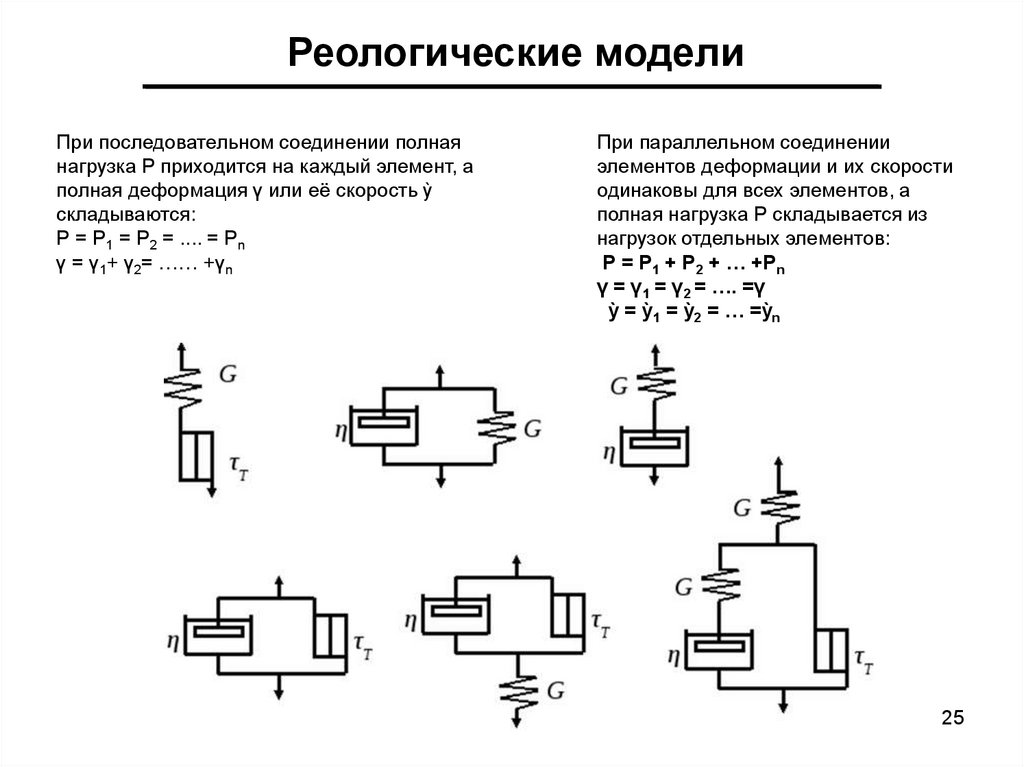
Реологические модели
При последовательном соединении полная
нагрузка Р приходится на каждый элемент, а
полная деформация γ или её скорость ỳ
складываются:
Р = Р1 = Р2 = .... = Рn
γ = γ1+ γ2= …… +γn
При параллельном соединении
элементов деформации и их скорости
одинаковы для всех элементов, а
полная нагрузка Р складывается из
нагрузок отдельных элементов:
Р = Р1 + Р2 + … +Рn
γ = γ1 = γ2 = …. =γ
ỳ = ỳ1 = ỳ2 = … =ỳn
25

26.

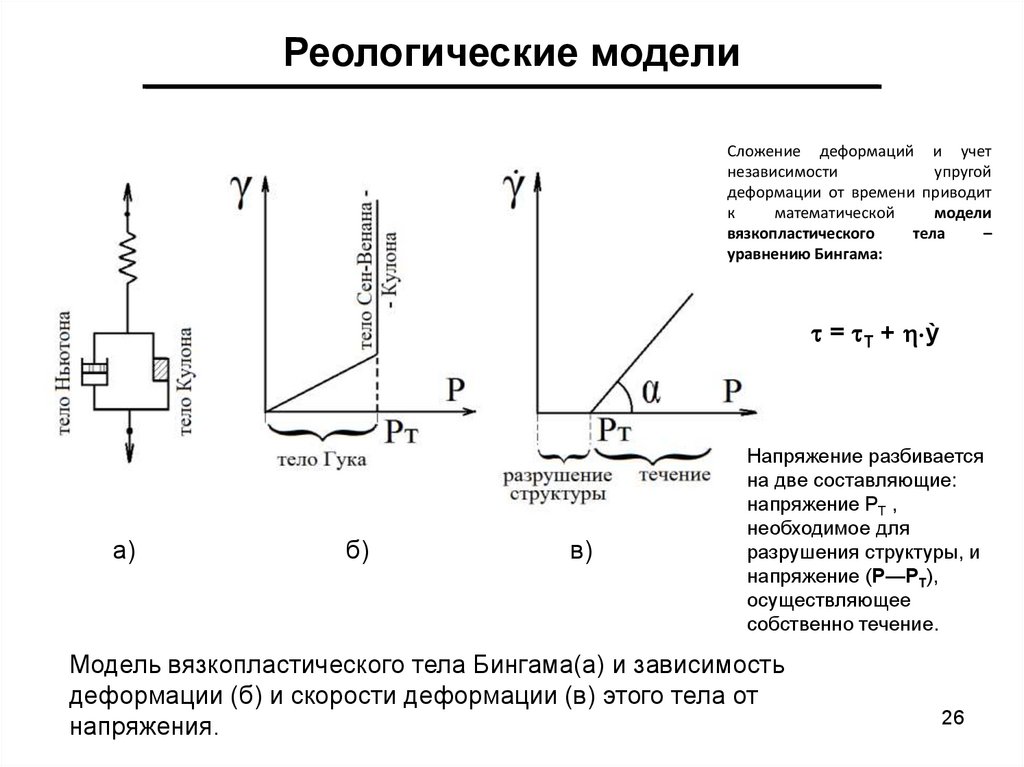
Реологические модели
Сложение деформаций и учет
независимости
упругой
деформации от времени приводит
к
математической
модели
вязкопластического
тела
–
уравнению Бингама:
= Т + ỳ
а)
б)
в)
Напряжение разбивается
на две составляющие:
напряжение РТ ,
необходимое для
разрушения структуры, и
напряжение (Р—РТ),
осуществляющее
собственно течение.
Модель вязкопластического тела Бингама(а) и зависимость
деформации (б) и скорости деформации (в) этого тела от
напряжения.
26

27.

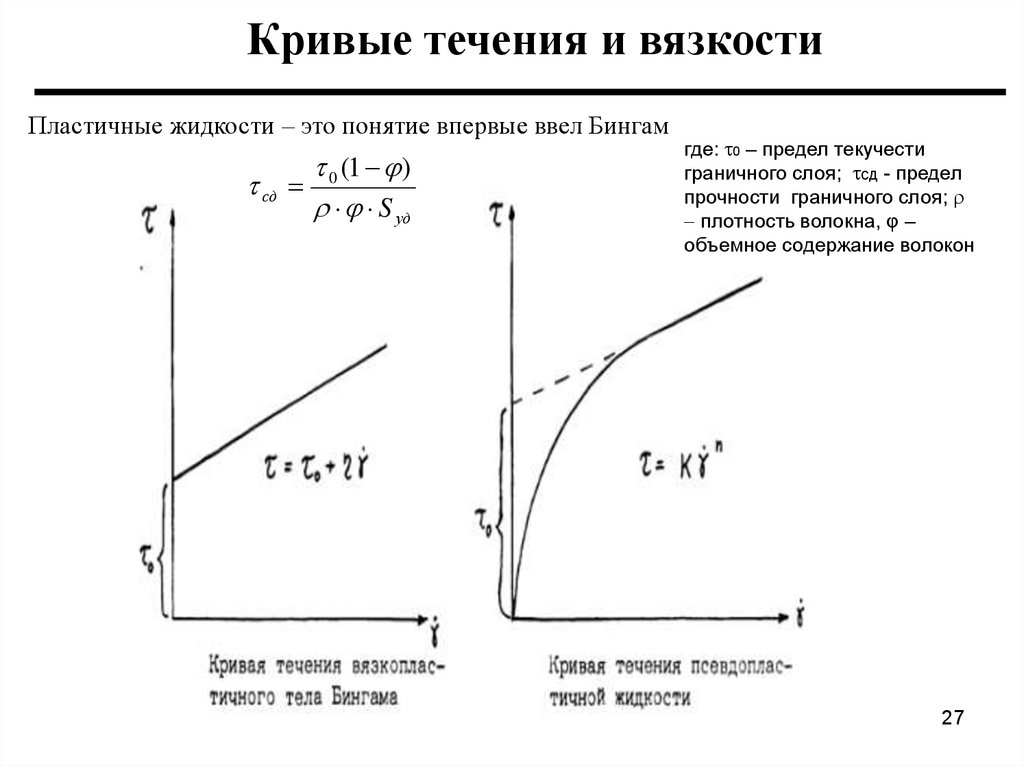
Кривые течения и вязкости
Пластичные жидкости – это понятие впервые ввел Бингам
сд
0 (1 )
S уд
где: 0 – предел текучести
граничного слоя; сд - предел
прочности граничного слоя;
плотность волокна, φ –
объемное содержание волокон
27

28.

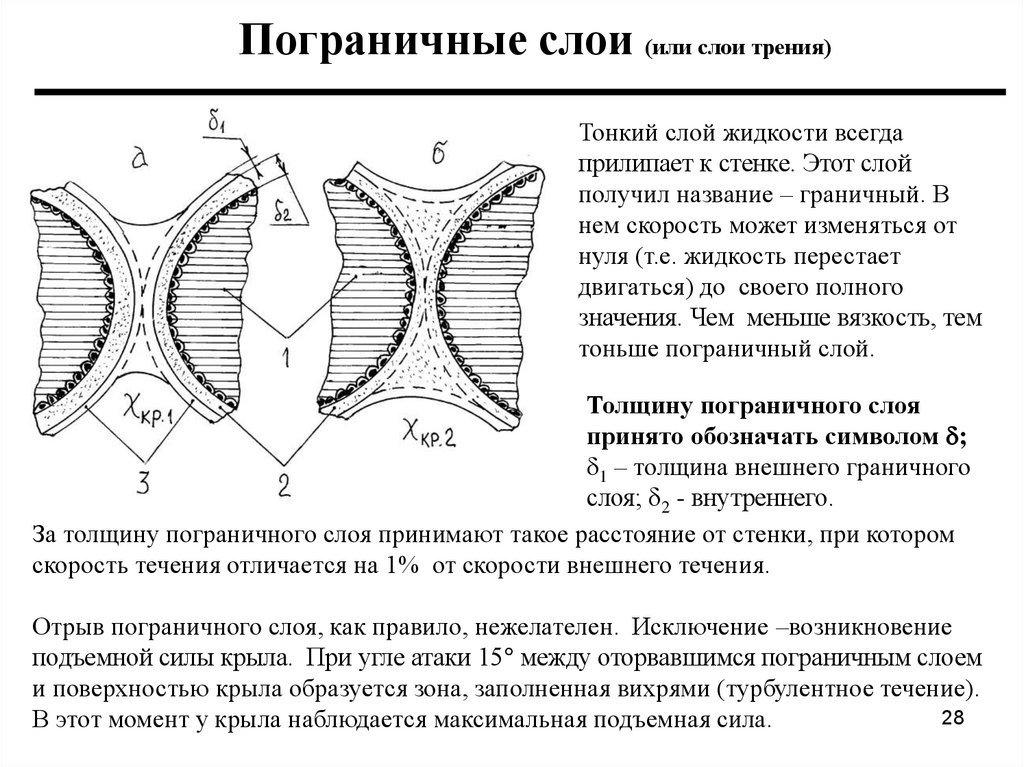
Пограничные слои (или слои трения)
Тонкий слой жидкости всегда
прилипает к стенке. Этот слой
получил название – граничный. В
нем скорость может изменяться от
нуля (т.е. жидкость перестает
двигаться) до своего полного
значения. Чем меньше вязкость, тем
тоньше пограничный слой.
Толщину пограничного слоя
принято обозначать символом ;
1 – толщина внешнего граничного
слоя; 2 - внутреннего.
За толщину пограничного слоя принимают такое расстояние от стенки, при котором
скорость течения отличается на 1% от скорости внешнего течения.
Отрыв пограничного слоя, как правило, нежелателен. Исключение –возникновение
подъемной силы крыла. При угле атаки 15 между оторвавшимся пограничным слоем
и поверхностью крыла образуется зона, заполненная вихрями (турбулентное течение).
28
В этот момент у крыла наблюдается максимальная подъемная сила.

29.

Законы капиллярного течения
Закон Дарси, описывает законы фильтрации жидкостей и газов в пористых
средах. Для ньютоновских жидкостей область применения закона Дарси
ограничивается малыми скоростями фильтрации (числа Рейнольдса),
рассчитанные по характерному размеру пор, меньше или порядка
единицы).
k P
V
l
2 cos
r
r cos 0,5
L
A 0,5
2
Рк
н
Уравнение Пуазейля
Закон Дарси
m L2
2 K P
Закон Лапласа
Уравнение Уошбурна
Q L
K
A P
Рк – капиллярное давление; поверхностное натяжение; краевой угол смачивания; r радиус капилляра;
V скорость ламинарного течения; Р перепад давления; L длина пути, пройденного жидкостью;
вязкость; время. V – скорость пропитки; k – капиллярное число, η- вязкость, l - длина капилляра; Q –
объемный расход жидкости, см3/сек; А – площадь сечения пропитываемого образца, см2; ΔР – перепад
давления, действующий на жидкость, кгс/см2; μ – вязкость жидкости; m – пористость армирующего
наполнителя, %.
29

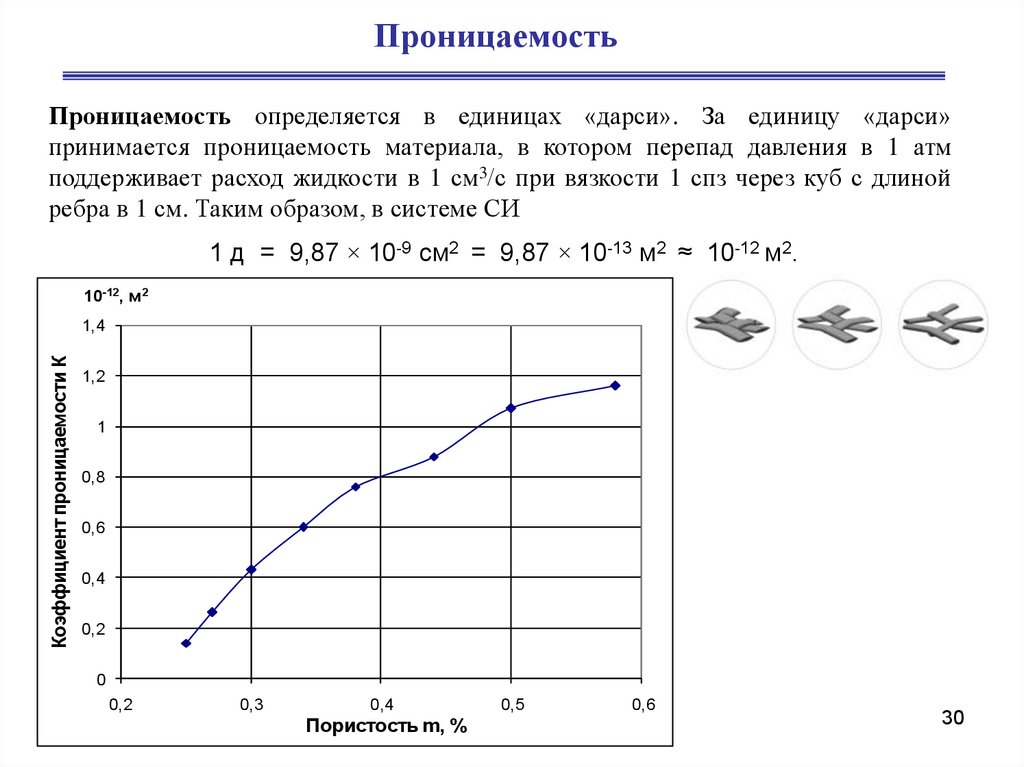
30.

Проницаемость
Проницаемость определяется в единицах «дарси». За единицу «дарси»
принимается проницаемость материала, в котором перепад давления в 1 атм
поддерживает расход жидкости в 1 см3/с при вязкости 1 спз через куб с длиной
ребра в 1 см. Таким образом, в системе СИ
1 д = 9,87 × 10-9 см2 = 9,87 × 10-13 м2 ≈ 10-12 м2.
10-12, м2
Коэффициент проницаемости К
1,4
1,2
1
0,8
0,6
0,4
0,2
0
0,2
0,3
0,4
Пористость m, %
0,5
0,6
30