Разные способы решения линейного тригонометрического уравнения

1.

МОУ СШ № 43 им. А. С. Пушкина
Разные способы решения
линейного тригонометрического
уравнения
Учитель математики
Страшко О.В.

2.

Тема: Некоторые способы решения
тригонометрических уравнений
Цель:
Проверить и закрепить умения и навыки
применения разных способов решения
линейных тригонометрических уравнений;
Поддержать в учащихся желание заниматься
математикой.

3.

Теоретическая часть
Вопросы

4.

Вопросы теоретической части
турнира
1. Какое уравнение называется
тригонометрическим?
2. Какая особенность решения тригонометрических
уравнений?
3. Какие тригонометрические уравнения называются
простейшими?
4. Что значит решить простейшее
тригонометрическое уравнение?

5.

Формула решения простейшего
тригонометрического уравнения.
5. При каких a данные уравнения имеют решения?
6. Решите простейшие тригонометрические уравнения

6.

Вопросы теоретической части
турнира
7. Какие тригонометрические уравнения называют
однородными?
8. Как решаются однородные уравнения n – степени
относительно синуса и косинуса?
9. Какие тригонометрические уравнения называются
линейными? Назовите способы решения
линейных тригонометрических уравнений.

7.

Практическая часть
Разные способы решения линейного
тригонометрического уравнения

8.

Приведение к одной
тригонометрической функции
Поскольку обе части уравнения были возведены в квадрат, могли
появиться посторонние корни. Значит, необходимо выполнить проверку.

9.

Способ приведения к одной
тригонометрической функции
Подставим каждый корень в заданное уравнение.
Ответ:
или

10.

Способ приведения к однородному
уравнению относительно синуса и косинуса
Ответ:
или

11.

Способ введения вспомогательного
аргумента
Ответ:
или

12.

Способ замены sin x и cos х на тангенс
половинного угла
1. Пусть

13.

Способ замены sin x и cos х на тангенс
половинного угла
2. Пусть
Подставим корень в исходное уравнение.
- тоже корень уравнения.
Следовательно,
Ответ:
или

14.

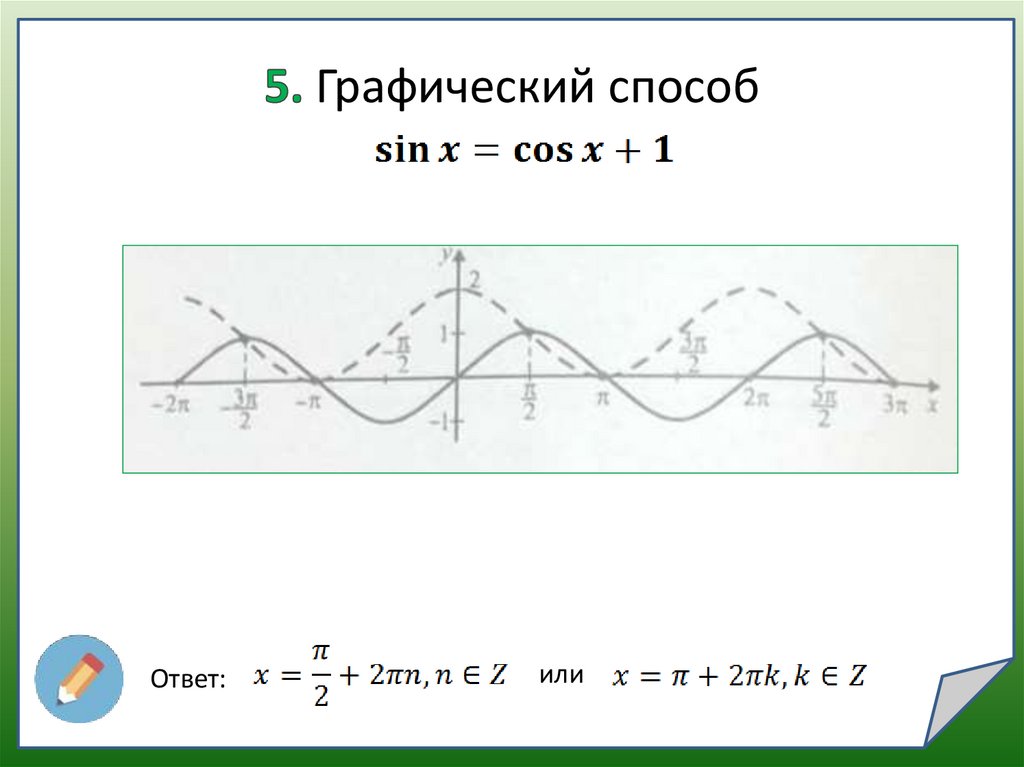
Графический способ
Ответ:
или

15.

Способ разложения на множители
Поскольку
то
Далее как в способе 2.
Ответ:
или

16.

Способ преобразования разности (суммы)
тригонометрических функций в произведение
Воспользуемся формулой разности синусов.
Далее как в способе 3.
Ответ:
или

17.

Способ возведения в квадрат обеих частей
уравнения
или
Поскольку обе части уравнения были возведены в квадрат, могли
появиться посторонние корни. Значит, необходимо выполнить проверку.

18.

Способ возведения в квадрат обеих частей
уравнения
Подставим каждый корень в заданное уравнение.
Ответ:
или

19.

Спасибо за внимание!