Похожие презентации:
Решение линейных уравнений с параметрами
1.
Решение линейныхуравнений с параметрами
воспитатель
Хриштейн Д.Я.
СПб ГКУЗ «ЦВЛ «Детская психиатрия» имени С.С. Мнухина
2.
Что такое параметр?Линейное уравнение с одной переменной — это уравнение вида
kx+b=0, где, x — переменная, а k и b — некоторые числа,
Называемые коэффициентами.
Решить уравнение – значит найти все значения переменной, при
которых уравнение превращается в верное числовое равенство
или показать, что их нет.
Количество корней линейного уравнения определятся значениями
коэффициентов k и b . Запишем эти условия:
b
при k≠0 и b≠0 линейное уравнение имеет единственный корень x=−
k
;
при k=0 и b≠0 линейное уравнение не имеет корней;
при k=0 и b=0 линейное уравнение имеет бесконечно много корней. Т.е. в
данном случае любое число может стать корнем линейного уравнения.
3.
Что такое параметр?Параметр – независимая величина, значение которой в задаче
считается заданным фиксированным или произвольным
действительным числом, или числом, принадлежащим заранее
оговоренному множеству.
Если в уравнении некоторые коэффициенты заданы не
конкретными числовыми значениями, а обозначены буквами, то
они называются параметрами , а уравнение параметрическим .
Например: ах+5=b
Решить уравнение с параметром – значит:
а) определить, при каких значениях параметров существуют
решения;
б) для каждой допустимой системы значений параметров найти
соответствующее множество решений.
4.
Что такое параметр?Линейное уравнение
Линейное уравнение с параметром
4х+8=0
x = 8/2
x=4
kx+8=0
k - параметр
Ответ: 4
Кол-во корней уравнения зависит от
значений параметра k.
Если k=0, то 0х+8=0
Корней нет.
Если k≠0, то kх+8=0
Имеет один корень х=-8/k
5.
Выразить переменную х в данных равенствахзадание
1. x a b
2. mx n
3. ax bx c
ax
4.
c
b
x
5. x c
b
px qx
6.
a
q
p
решение
1. x b a
2. x
3. x
4. x
5. x
6. x
n
m
c
a b
bc
a
bc
b 1
aqp
2
2
p q
6.
Что такое параметр?Типы задач с параметрами
• решить для любого значения параметра;
• определить количество решений в зависимости от значения
параметра;
• требуется найти все те значения параметра, при которых
указанные уравнения, неравенства, их системы и совокупности
имеют заданное число решений;
• уравнения, неравенства, их системы и совокупности, для
которых при искомых значениях параметра множество решений
удовлетворяет заданным условиям в области определения.
7.
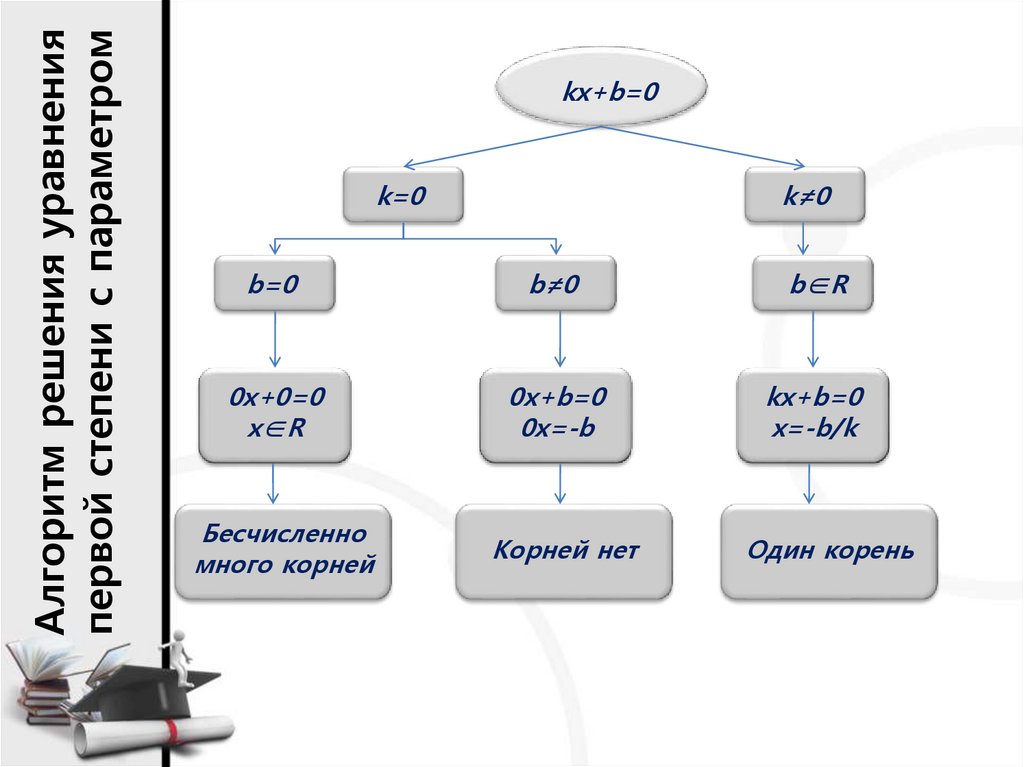
Алгоритм решения уравненияпервой степени с параметром
kx+b=0
k=0
k≠0
b=0
b≠0
b∈R
0x+0=0
x∈R
0x+b=0
0x=-b
kx+b=0
x=-b/k
Бесчисленно
много корней
Корней нет
Один корень
8.
ЗадачиРешить уравнение:
ах 1 0
5х а 0
5 х а
ах 1
если а 0, то решений нет
если а 0, то х
х
1
а
Ответ : при а 0 решений нет, при а 0 х
1
.
а
а
5
Ответ : при а R x
Для каждого значения параметра а найдите количество корней
уравнения:
ах 7 1 3а
x
3a 6
a
Ответ : при а 0 один корень х
ппр а 0 ккорней н ет.
-3а-6
а
a
5
9.
ЗадачиОпределить при каких значениях параметра a
уравнение имеет положительные корни
5( x 3) 3(3x 2a)
Определить при каких значениях параметра a
уравнение имеет отрицательные корни
8х ах 8 а 3
Решение :
Решение :
1. 5 x 15 9 x 6a
1. 8 х-ах 8-а 3
4 x 15 6a
х(8 а ) (8 а ) 3
6a 15
x
4
( х 1)(8 а ) 3
2.
6 a 15
0
4
6 a 15
a 2,5
Ответ : при а 2,5 х 0
3
8 а
3 8 а
х
8 а
а 5
х
8 а
а 5
0
8 а
2.
+
5
x 1
Ответ : при а ; 5 (8; ) х 0
8
-
10.
ЗадачиРешить линейное уравнение с параметром:
1. а 2 х а 3 2ах 3 х
2. 10 х-7 ах 5 а-а 2 х
3. 3 а 2 х а 8ах 15
4. ( р 2 1) х р 3 1
При каких значениях параметров а и b уравнение не имеет
решений
5. ( 2а b)x a b-1
Исследовать при каких значениях параметров уравнение имеет
положительные, отрицательные, нулевые, бесконечные решения.
6. 3ах b b(a x)









 Математика
Математика








