Статистические критерии различий. Непараметрические критерии для несвязных выборок

1. Статистические критерии различий. Непараметрические критерии для несвязных выборок

СТАТИСТИЧЕСКИЕ КРИТЕРИИ
РАЗЛИЧИЙ.
НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ
ДЛЯ НЕСВЯЗНЫХ ВЫБОРОК

2. План

ПЛАН
Критерий Розенбаума Q .
2. Критерий U Манна-Уитни.
3. Критерий H Крускала-Уоллиса.
4. Критерий тенденций Джонкира S.
1.

3. Критерии Q

КРИТЕРИИ Q
Работа с критерием Розенбаума предполагает подсчет так
называемых «хвостов». Поэтому этот критерий еще носит название
«критерий хвостов».
Расположим данные, полученные в результате эксперимента друг
под другом для каждой выборки. В том случае если в сравниваемых
рядах будут равные элементы, их следует размещать точно друг под
другом.
ххххх|ххххххх|
S
T
|ууууууу|уууууууу
Выбор расположения произволен. В обоих случаях символы Т и S
обозначают соответственно левый и правый «хвосты». Они
подсчитываются так величина Т равна числу элементов ряда х, которые
находятся левее начала совпадающих элементов в ряду у, величина S —
соответственно равна числу элементов, которые находятся в ряду у,
правее конца совпадающих элементов.
Таким образом, величина Т «левого» хвоста равна 5.Величина S
«правого» хвоста данных равна 8.
Qэмп– это сумма величин S и Т.
Qэмп = S + Т

4. Критерии Q

КРИТЕРИИ Q
Рассмотрим следующее расположение данных
полученных у двух выборок испытуемых:
хххххххххххх
ууууууууууууууу
Поскольку в этом случае между
элементами обоих рядов нет пересечений
(одинаковых элементов), то между этими
двумя рядами будет статистически значимое
различие.
А хвостами можно считать длины рядов х и y.

5. Критерии Q

КРИТЕРИИ Q
Задача. Используя тест Векслера психолог определил показатели
интеллекта у двух групп, учащихся из разных школ. Его интересует ответ
на вопрос – будут ли обнаружены статистически значимые различия в
показателях интеллекта?
Решение.
Из первой школы было выбрано 11 школьников, а из второй – 12.
Результаты измерений сразу представим в удобном для расчета критерия
Q виде, т.е. расположив числа в порядке возрастания слева направо и
одно измерение под другим
Т
|96, 100, 104, 104, 120,120, 120, 120,|126,130, 134
76, 82, 82, 84, 88,|96, 100, 102, 104, 110, 118, 120| S
В этом случае S=3, Т=5, Qэмп = 3+5 = 8

6. Критерии Q

КРИТЕРИИ Q
Критические значения:
Qкр =7, для Р < 0,05,
Qкр =9, для Р < 0,01
Ось значимости
Зона
незначимости
Зона
неопределенности
0,05
Qкр =7
0,01
Qэмп=8
Qкр =9
Зона
значимости

7. Критерии Q

КРИТЕРИИ Q
Qэмп попало в зону неопределенности, можно
принять гипотезу H1 о различии.
H1 : существуют статистически значимые различия
в уровне интеллекта у учащихся двух школ.
Различия зафиксированы на уровне значимости
0,05.
Ответ: согласно критерию Q установлены различия в
уровне интеллекта у учащихся двух школ на уровне
значимости 0,05.

8. Алгоритм использования критерия Q

АЛГОРИТМ ИСПОЛЬЗОВАНИЯ КРИТЕРИЯ Q
1.Упорядочить экспериментальные данные для каждой выборки.
2.Расположить полученные ряды чисел друг под другом и «отсечь
хвосты».
3. Определить длины «хвостов».
4. Вычислить Qэмп как сумму длин «хвостов».
5. Построить ось значимости (направление оси - слева направо).
6. Сделать вывод о принятии нулевой или альтернативной гипотез.
7. Интерпретировать задачу.

9. Для применения критерия Q необходимо соблюдать следующие условия:

ДЛЯ ПРИМЕНЕНИЯ КРИТЕРИЯ Q НЕОБХОДИМО
СОБЛЮДАТЬ СЛЕДУЮЩИЕ УСЛОВИЯ:
1.
2.
3.
4.
5.
Измерение может быть проведено в шкале порядка,
интервалов и отношений.
Выборки должны быть независимыми.
В каждой из выборок должно быть не меньше 11
испытуемых.
Верхний предел выборки, в зависимости от таблицы
приложений, может ограничиться 26 испытуемыми.
При числе наблюдений (испытуемых) в каждой
выборке больше 26 можно пользоваться
следующими величинами QK =8 для р<0,05 и QK =10
для р<0,01

10. Критерий U Манна-Уитни

КРИТЕРИЙ U МАННА-УИТНИ
Критерий U является более мощным, чем критерий
Розенбаума.
Этот критерий применяют для оценки различий по
уровню выраженности какого-либо признака для двух
независимых (несвязных) выборок. При этом выборки
могут различаться по числу входящих в них испытуемых.
Этот критерий особенно удобен в том случае, когда число
испытуемых невелико и в обеих выборках не превышает
величину 20, хотя таблицы критических значений
рассчитаны для величин выборок, не превышающих 60
человек испытуемых.
Данный метод выявления различий между
выборками был предложен в 1945 году Фрэнком
Уилкоксоном (F. Wilcoxon). В 1947 году он был
существенно переработан и расширен Х.Б.Манном
(H. B. Mann) и Д.Р.Уитни (D. R. Whitney), по именам
которых и называется.

11. Критерий U Манна-Уитни

КРИТЕРИЙ U МАННА-УИТНИ
Задача. Две неравные по численности группы испытуемых
решали техническую задачу. Показателем успешности
служило время решения. Испытуемые меньшей по
численности группы получали дополнительную мотивацию в
виде денежного вознаграждения. Психолога интересует
вопрос — влияет ли вознаграждение на успешность решения
задачи.
Решение: Психологом были получены следующие результаты
времени решения технической задачи в секундах в первой
группе — с дополнительной мотивацией - 39, 38, 44, 6, 25,
25, 30, 43, во второй группе — без дополнительной
мотивации — 46, 8, 50, 45 32, 41, 41, 31, 55 Число
испытуемых в первой группе - 8, во второй 9.

12. Критерий U Манна-Уитни

КРИТЕРИЙ U МАННА-УИТНИ
Первый способ расчета по критерию U
Полученные данные необходимо объединить, т. е.
представить как один ряд и упорядочить его по
возрастанию входящих в него величин.
Для критерия U важны не сами численные значения
данных, а порядок их расположения.
Предварительно обозначим каждый элемент первой
группы символом х, а второй — символом у. Тогда
общий упорядоченный по возрастанию численных
величин ряд можно представить так
Х у х х х у у х х у у х х у у у у
6 8 25 25 30 31 32 38 39 41 41 43 44 45 46 50 55

13. Критерий U Манна-Уитни

КРИТЕРИЙ
U МАННА-УИТНИ
Группа с дополнительной
Группа без
Инверсия X/Y
№1
мотивацией
№2
№3
№4
Инверсия Y/X
6
-
дополнительной
мотивации
8
0
-
1
25
-
1
-
25
-
1
-
30
-
1
-
-
31
-
4
-
32
-
4
38
-
3
-
39
-
3
-
-
41
-
6
-
41
-
6
43
-
5
-
44
-
5
-
-
45
-
8
-
46
-
8
-
50
-
8
-
55
-
8
19
53
Суммы инверсий

14. Критерий U Манна-Уитни

КРИТЕРИЙ U МАННА-УИТНИ
Критические значения:
Uкр =18, для Р< 0 05,
Uкр =11, для Р < 0,01
Uэмп =19 (наименьшее значение из сумм инверсий)
Ось значимости
Зона
Зона
незначимости
Uэмп=19
неопределенности
0,05
0,01
Uкр =18
Uкр =11
Зона
значимости

15. Критерий U Манна-Уитни

КРИТЕРИЙ U МАННА-УИТНИ
Uэмп попало в зону незначимости, нужно принять
гипотезу H0 о сходстве.
H0 : не существует статистически значимых
различий во времени решения задач у двух
групп испытуемых.
Ответ: согласно критерию U установлено, что не
существует статистически значимых различий во
времени решения задач, а значит
вознаграждение не влияет на успешность
решения задачи.

16. Критерий U Манна-Уитни (второй способ расчета)

КРИТЕРИЙ U МАННА-УИТНИ (ВТОРОЙ СПОСОБ
РАСЧЕТА)
Преимущество второго способа подсчета по
критерию U наиболее отчетливо проявляется
в тех случаях, когда две или большее
количество одинаковых величин будут входить
в оба сравниваемых ряда.

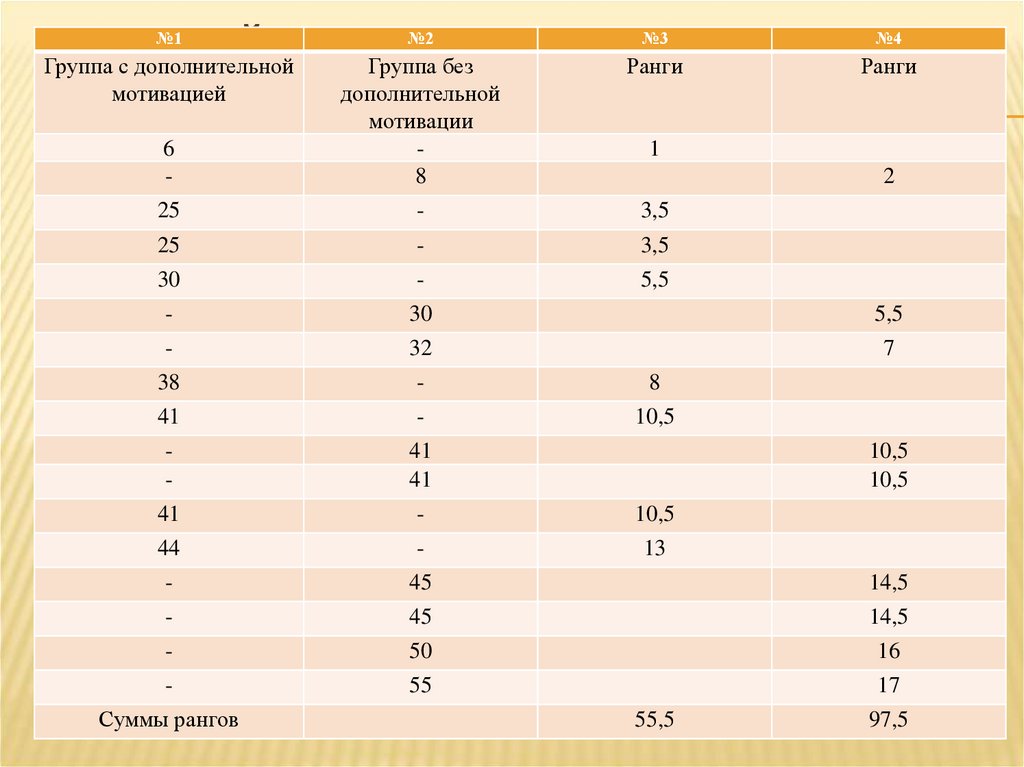
17. Критерий U Манна-Уитни

КРИТЕРИЙ
U МАННА-УИТНИ
Группа с дополнительной
Группа без
Ранги
№1
мотивацией
№2
№3
№4
Ранги
6
-
дополнительной
мотивации
8
25
-
3,5
25
-
3,5
30
-
5,5
-
30
5,5
-
32
7
38
-
8
41
-
10,5
-
41
41
41
-
10,5
44
-
13
-
45
14,5
-
45
14,5
-
50
16
-
55
17
Суммы рангов
1
2
10,5
10,5
55,5
97,5

18. Критерий U Манна-Уитни

КРИТЕРИЙ U МАННА-УИТНИ
Следующим этапом, является проверка его правильности. Для этого
Подсчитывается общая сумма рангов из таблицы
55,5 + 97,5= 153
Рассчитывается сумма рангов по формуле
N ( N 1) 17 18
153
2
2
N n1 n2
Поскольку расчетные суммы случаев совпали, то ранжирование было проведено
правильно.
Затем находится наибольшая по величине ранговая сумма. Она обозначается
как Rmaх . В нашем случае она равна 97,5.
UЭМП вычисляется по следующей формуле
n ( n 1)
9 10
U эмп ( n1 n2 ) x x
Rmax (8 9)
97,5 19,5
2
2
Где n1 – численное значение первой выборки,
n2 – численное значение второй выборки,
Rmax – наибольшая по величине сумма рангов,
nx – количество испытуемых в группе с большей суммой рангов

19. Критерий U Манна-Уитни

КРИТЕРИЙ U МАННА-УИТНИ
Критические значения:
Uкр =18 для Р < 0,05,
Uкр =11 для Р < 0,01
Ось значимости
Зона
Зона
незначимости
Uэмп=19,5
неопределенности
0,05
0,01
Uкр =18
Uкр =11
Зона
значимости

20.

Uэмп попало в зону незначимости, нужно принять можно
принять гипотезу H0 о сходстве.
H0 : не существует статистически значимых различий во
времени решения задач у двух групп испытуемых.
Ответ: согласно критерию U установлено, что не существует
статистически значимых различий во времени решения
задач, а значит вознаграждение не влияет на успешность
решения задачи.

21. Для применения Критерия U Манна-Уитни необходимо соблюдать следующие условия:

ДЛЯ ПРИМЕНЕНИЯ КРИТЕРИЯ U МАННА-УИТНИ
НЕОБХОДИМО СОБЛЮДАТЬ СЛЕДУЮЩИЕ
УСЛОВИЯ:
1. Измерение должно быть проведено в шкале
интервалов или отношений.
2. Выборки должны быть несвязанными.
3. Нижняя граница применимости критерия
для каждой группы испытуемых – 3
человека.
4. Верхняя граница применимости критерия –
60 человек.

22. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
Критерий Н применяется для оценки
различий по степени выраженности
анализируемого признака одновременно
между тремя, четырьмя и более выборками.
Он позволяет выявить степень изменения
признака в выборках, не указывая, однако,
на направление этих изменений.

23. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
Работа с данными начинается с того, что все выборки
условно объединяются по порядку встречающихся
величин в одну выборку и значениям этой
объединенной выборки проставляются ранги. Затем
полученные ранги проставляются исходным выборочным данным, и по каждой выборке отдельно
подсчитывается сумма рангов. Критерий построен на
следующей идее — если различия между выборками
незначимы, то и суммы рангов не будут существенно
отличаться одна от другой и наоборот.

24. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
Задача Четыре группы испытуемых
выполняли тест Бурдона в разных
экспериментальных условиях. Задача в том,
чтобы установить — зависит ли
эффективность выполнения теста от условий
или, иными словами, существуют ли
статистически достоверные различия в
успешности выполнения теста между
группами. В каждую группу входило четыре
испытуемых.

25. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
Номер
1 группа
испытуемого
2 группа
3 группа
4 группа
1
23
45
34
21
2
20
12
24
22
3
34
34
25
26
4
35
11
40
27
Суммы
112
102
123
96

26. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
Для дальнейшей работы с критерием необходимо построить
все полученные значения и один столбец по порядку и
проставить им pанги.
Данные
11
12
20
21
22
23
24
25
Ранги
1
2
3
4
5
6
7
8
Данные
26
27
34
34
34
35
40
45
Ранги
9
10
12
12
12
14
15
16

27. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
№
1 группа Ранги
испытуе
мых
2 группа Ранги
3 группа Ранги
4 группа Ранги
1
23
6
45
16
34
12
21
4
2
20
3
12
2
24
7
22
5
3
34
12
34
12
25
8
26
9
4
35
14
11
1
40
15
27
10
Сумм 112
ы
35
102
31
123
42
96
28

28. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
Теперь можно подсчитать величину Нэмп по
формуле
12
R2
Hэмп
3( N 1)
N ( N 1)
n
Где N – общее число членов в обобщенной
выборке, п – число членов в каждой
отдельной выборке
2
R – квадраты сумм рангов по каждой
отдельной выборке.

29. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
352 312 422 282
12
Hэмп
3 16 1 1, 21
16(16 1) 4
4
4
4
7,815, для _ р 0,05
H кр
11,345, для _ р 0,01
При определении критических значении критерия
Н применительно к четырем и более выборкам
используют таблицу для критерия хи-квадрат
Пирсона, подсчитав предварительно число
степеней свободы v для с = 4 Тогда v = c— 1=4— 1
= 3.

30. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
7,815, для _ р 0,05
H кр
11,345, для _ р 0,01
Зона
незначимости
Зона
неопределенности
0,05
Нэмп=1,21 Нкр =7,815
0,01
Нкр =11,345
Зона
значимости

31. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
Полученное эмпирическое значение оказалось существенно
меньше
критического
значения
для
5%
уровня.
Следовательно, можно утверждать, что различии по
показателю переключаемости внимания между группами нет.
Переформулируем полученный результат в терминах нулевой
и альтернативной гипотез. Поскольку между показателями,
измеренными в четырех разных условиях, существуют лишь
случайные различия то принимается нулевая гипотеза H0, т.е.
гипотеза о сходстве. Иными словами, различные условия
проведения тесы Бурдона не влияют на показатели
переключаемости внимания.

32. Алгоритм использования Критерия H Крускала-Уоллиса

АЛГОРИТМ ИСПОЛЬЗОВАНИЯ КРИТЕРИЯ H
КРУСКАЛА-УОЛЛИСА
1.Объединить все данные в одну выборку и
проранжировать.
2.Вернуть ранги в исходную таблицу.
3. Просуммировать ранги для каждой группы
испытуемых.
4. Вычислить Hэмп по формуле.
5. Построить ось значимости (направление оси - слева
направо).
6. Сделать вывод о принятии нулевой или
альтернативной гипотез.
7. Интерпретировать задачу.

33. Критерий H Крускала-Уоллиса

КРИТЕРИЙ H КРУСКАЛА-УОЛЛИСА
1.
2.
3.
4.
5.
6.
Для использования критерия Н необходимо соблюдать следующие
условия:
Измерение должно быть проведено в шкале порядка, интервалов или
отношений.
Выборки должны быть независимыми.
Допускается разное число испытуемых в сопоставляемых выборках.
При сопоставлении трех выборок допускается, чтобы в одной из них
было n = 3, а в двух других n = 2. Однако, в таком случае различия могут
быть зафиксированы лишь на 5% уровне значимости.
Максимальное число испытуемых во всех трех выборках, может быть 5.
При большем числе выборок и разном количестве испытуемых в каждой
выборке следует пользоваться таблицей для критерия хи- квадрат. В этом
случае число степеней свободы определяется по формуле v=с-1, где с —
количество сопоставляемых выборок.

34. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
Этот критерий ориентирован на выявление тенденций
изменения измеряемого признака при сопоставлении от трех
до шести выборок.
В отличие от предыдущего критерия, количество
элементов в каждой выборке должно быть одинаковым.
Если же число элементов каждой выборке различно, то
необходимо случайным образом уравнять выборки, при этом
неизбежно утрачивается часть информации.
Если же потеря информации покажется слишком
расточительной, то следует воспользоваться
вышеприведенным критерием Н – Крускала-Уоллиса, хотя в
этом случае нельзя будет выдвигать гипотезу о наличии или
отсутствии искомых тенденции.

35. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
Критерий S основан на следующем принципе все выборки
располагаются слева направо в порядке возрастания значений
исследуемого признака. При этом выборка, в которой среднее значение
или сумма всех значений меньше чем в остальных выборках,
располагается слева, а выборка, в которой эти же значения выше,
располагается правее и так далее.
После такого упорядочивания для каждого отдельного элемента,
стоящего слева в выборке, подсчитывается число инверсии по отношению
ко всем элементам упорядоченных выборок, расположенных правее.
Инверсией для данного элемента выборки считается число
элементов, которые превышают данный элемент по величине по всем
выборкам справа. Инверсии по отношению к собственной выборке, т.е.
той, в которой находится данный элемент, не подсчитываются. В
соответствии с этим правилом у последнего столбца выборки инверсии
также не подсчитываются, т. к. справа больше нет данных.

36. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
Задача. Установить наблюдается ли тенденция
к увеличению ошибок при выполнении теста
Бурдона разными испытуемыми в
зависимости от условии его выполнения.

37. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
Номер
1 группа
испытуемого
2 группа
3 группа
4 группа
1
23
45
34
21
2
20
12
24
22
3
34
34
25
26
4
35
11
40
27
Суммы
112
102
123
96

38. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
Номер
4 группа
испытуемого
2 группа
1 группа
3 группа
1
21
45
23
34
2
22
12
20
24
3
26
34
34
25
4
27
11
35
40
Суммы
96
102
112
123

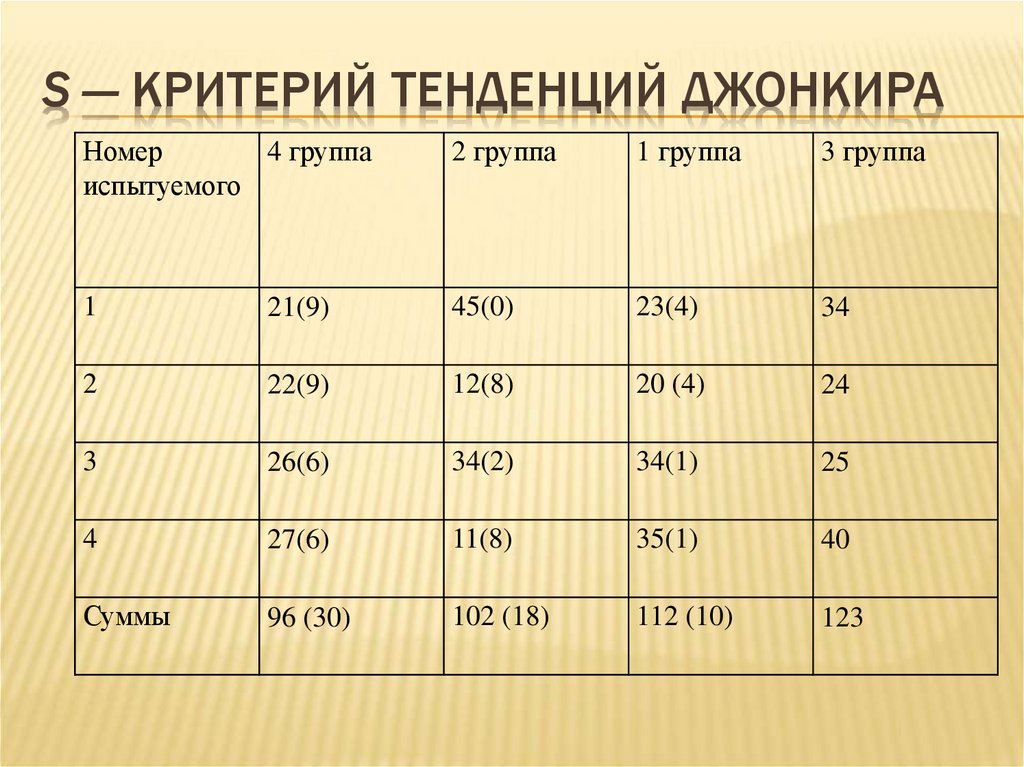
39. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
Номер
4 группа
испытуемого
2 группа
1 группа
3 группа
1
21(9)
45(0)
23(4)
34
2
22(9)
12(8)
20 (4)
24
3
26(6)
34(2)
34(1)
25
4
27(6)
11(8)
35(1)
40
Суммы
96 (30)
102 (18)
112 (10)
123

40. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
Следующий этап – подсчет общей суммы
получившихся инверсии. Это число
обозначается как А. В нашей задача оно равно
А =30+18+10 = 58
Величина Sэмп критерия вычисляется по
формуле Sэмп=2А-В.
В формуле символ В также представляет
собой выражение B с(с 1) n
2
n — количество элементов в столбце (группе).
с — количество столбцов (групп).
2

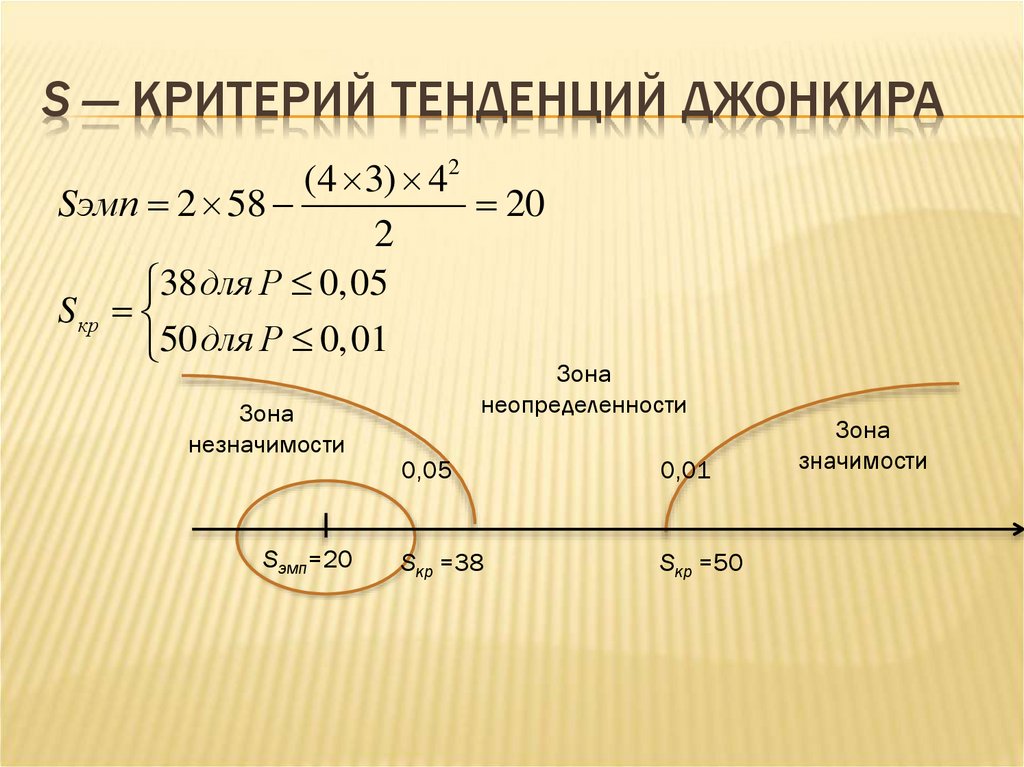
41. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
(4 3) 42
Sэмп 2 58
20
2
38 для Р 0,05
Sкр
50 для Р 0,01
Зона
незначимости
Sэмп=20
Зона
неопределенности
0,05
0,01
Sкр =38
Sкр =50
Зона
значимости

42. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
Согласно полученному результату Sэмп
попало в зону незначимости, следовательно,
принимается гипотеза Н0 о том, что тенденция
к увеличению числа ошибок в тесте Бурдона в
зависимости от условий его выполнения, не
выявлена.

43. Алгоритм использования S — критерия тенденций Джонкира

АЛГОРИТМ ИСПОЛЬЗОВАНИЯ S — КРИТЕРИЯ
ТЕНДЕНЦИЙ ДЖОНКИРА
1.Расположить выборки в порядке возрастания их сумм (или
средних значений).
2.Выполнить подсчет инверсий для каждого столбца, соотнося
данные со столбцами, расположенными правее рабочего.
3. Просуммировать инверсии для каждой группы испытуемых.
4. Вычислить Sэмп по формуле.
5. Построить ось значимости (направление оси - слева направо).
6. Сделать вывод о принятии нулевой или альтернативной
гипотез.
7. Интерпретировать задачу.

44. S — критерий тенденций Джонкира

S — КРИТЕРИЙ ТЕНДЕНЦИЙ ДЖОНКИРА
Для использования критерия S необходимо соблюдать
следующие условия:
1. Измерение может быть произведено в шкале порядка,
интервалов и отношений.
2. Выборки должны быть независимыми.
3. Количество элементов в каждой выборке должно быть
одинаковым. Если это не так, то необходимо случайным
образом уравнять выборки.
4. Нижняя граница применимости критерия не менее трех
выборок и не менее двух элементов в каждом наблюдении.
Верхняя граница определяется таблицей – не более 6
выборок и не более 10 элементов в каждой выборке. Во всех
других случаях следует пользоваться критерием Н.

45.

Спасибо за внимание!