Похожие презентации:
Статистические критерии различий. Непараметрические критерии для связных выборок
1. Статистические критерии различий. Непараметрические критерии для связных выборок
СТАТИСТИЧЕСКИЕ КРИТЕРИИРАЗЛИЧИЙ.
НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ
ДЛЯ СВЯЗНЫХ ВЫБОРОК
2. План
ПЛАН1.Статистические критерии различий.
1.1 Понятие статистического критерия различий и
классификация критериев.
1.2 Рекомендации к выбору критерия различий.
2.Непараметрические критерии для связанных
выборок.
2.1 Критерий знаков G.
2.2 Парный критерий Т – Вилкоксона.
2.3 Критерий Фридмана.
2.4 Критерий Пейджа.
2.5 Критерий Макнамары.
3.
Статистические способы, позволяющие оценить степеньстатистической достоверности изменения того или иного
показателя (в частности психологического) в одной или
нескольких группах или выявить динамику изменения
показателя под влиянием экспериментальных воздействий
называются статистическими критериями различий.
Критерии различаются по следующим основаниям:
- по типу измерительной шкалы;
- по объему выборки (максимальный и минимальный);
- по количеству выборок;
- по качеству выборки (связные, несвязные);
- по мощности;
- по использованию типа распределения и его параметров
(параметрические и непараметрические).
4.
Мощность критерия — это его способность выявлятьразличия или отклонять нулевую гипотезу, если она
неверна(мощность критерия характеризует его
способность избегать ошибок второго рода).
Чем мощнее критерий, тем более трудоемкой
является процедура вычислений с его помощью.
Более того, если значимые различия установлены с
помощью менее мощного критерия, то более
мощный, заведомо подтвердит факт существования
этих различий. Следовательно использование менее
мощных критериев нередко бывает оправданным
(прежде всего в целях экономии времени
вычислений).
5.
Критерии различия называют параметрическимесли он основан на конкретном типе
распределения генеральной совокупности (как
правило нормальном) или использует параметры
этой
совокупности
(среднее
значение,
дисперсию и т.д.)
Критерий
различия
называют
непараметрическим (критерий свободный от
распределения) если он не базируется на
предположении
о
типе
распределения
генеральной совокупности и не использует
параметры этой совокупности.
6.
Принормальном
распределении
генеральной
совокупности параметрические критерии обладают
большей
мощностью
по
сравнению
с
непараметрическими. По этой причине, в тех случаях
когда выборки взяты из нормально распределенных
генеральных
совокупностей,
следует
отдавать
предпочтение параметрическим критериям.
Однако, как показывает практика, подавляющее
большинство данных получаемых в психологических
экспериментах не распределены нормально, поэтому
применение параметрических критериев при анализе
результатов
психологических
исследовании
может
привести к ошибкам в статистических выводах. В таких
случаях непараметрические критерии оказываются более
мощными, т. е. способными с большей достоверностью
отвергать нулевую гипотезу.
7. Рекомендации к выбору критерия различий:
РЕКОМЕНДАЦИИ К ВЫБОРУ КРИТЕРИЯ РАЗЛИЧИЙ:прежде всего, определить, является ли выборка связной (зависимой) или
несвязной (независимой);
определить однородность, неоднородность выборки;
оценить объем выборки и, зная ограничения каждого критерия по
объему, выбрать соответствующий критерий;
целесообразнее всего начинать работу с выбора наименее трудоемкого
критерия;
если используемый критерий не выявил различия — следует применить
более мощный, но одновременно и более трудоемкий критерий;
если в распоряжении психолога имеется несколько критериев, то следует
выбирать те из них, которые наиболее полно используют информацию,
содержащуюся в экспериментальных данных.
при малом объеме выборки следует увеличивать величину уровня
значимости (не менее 1%) так как небольшая выборка и низкий уровень
значимости приводят к увеличению вероятности принятия ошибочных
решений.
8. Критерии знаков G
КРИТЕРИИ ЗНАКОВ GЗадача. Психолог проводит групповой
тренинг. Его задача — выяснить будет ли
эффективен данный конкретный вариант
тренинга для снижения уровня тревожности
участников?
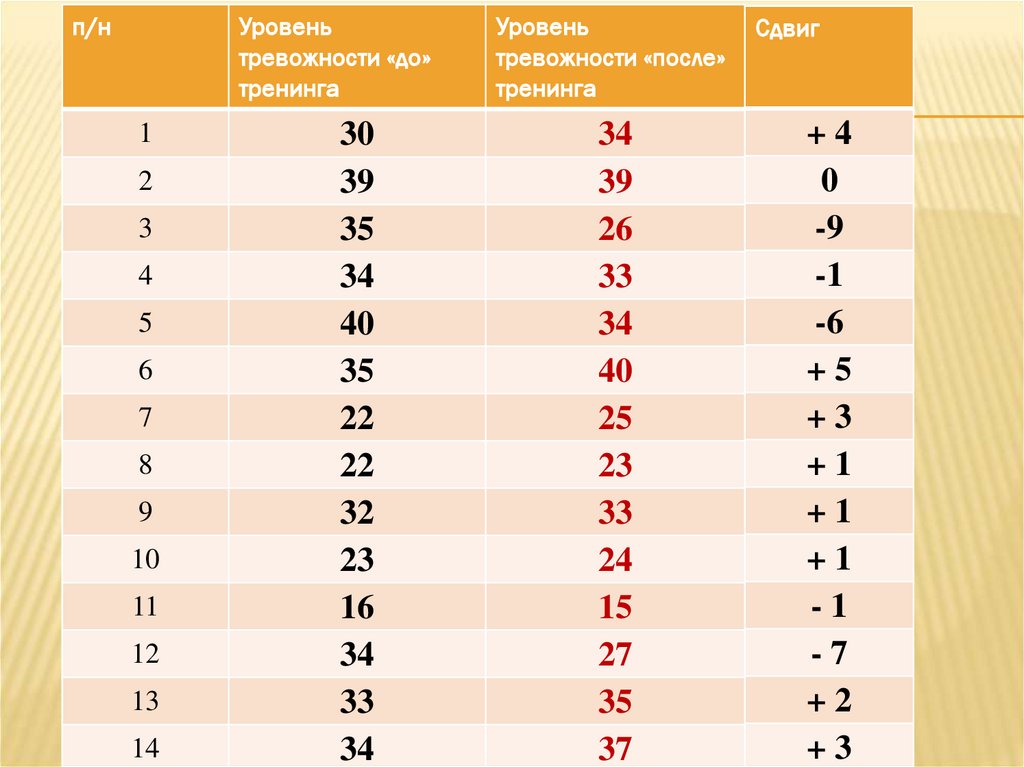
Решение. Для решения этой задачи психолог
с помощью теста Тейлора дважды выявляет
уровень тревожности у 14 участников до и
после проведения тренинга. Результаты
измерения приведены в таблице.
9.
п/нУровень
тревожности «до»
тренинга
1
2
3
4
5
6
7
8
9
10
11
12
13
14
30
39
35
34
40
35
22
22
32
23
16
34
33
34
Уровень
тревожности «после»
тренинга
34
39
26
33
34
40
25
23
33
24
15
27
35
37
Сдвиг
+4
0
-9
-1
-6
+5
+3
+1
+1
+1
-1
-7
+2
+3
10.
Сдвиг — это величина разности между показателямипризнака одного и того же участника после и до
тренинга. Но не наоборот. Величины сдвигов
обязательно должны быть даны в соответствующем
столбце таблицы с учетом знаков.
Количество положительных сдвигов - 8
Количество отрицательных сдвигов – 5
Типичный сдвиг (наиб. знач. найденных чисел) – 8
Нетипичный сдвиг (наим. знач. найденных чисел) –
5 = Gэмп
11.
Критические значения:Gкр =3 для Р < 0,05,
Gкр =1 для Р < 0,01
Ось значимости
Зона
незначимости
Gэмп=5
Зона
неопределенности
0,05
0,01
Gкр =3
Gкр =1
Зона
значимости
12.
Gэмп попало в зону незначимости т.е. полученный вэксперименте общий положительный сдвиг, который
соответствует увеличению уровня тревожности
испытуемых после проведения тренинга
статистически недостоверен.
Т. о.должна быть принята гипотеза H0 об отсутствии
различий или о наличии сходства.
Возвращаясь к условию задачи, сформулируем
Ответ: согласно критерию знаков G, примененный
психологом способ тренинга неудовлетворителен,
поскольку не дает статистически достоверных
изменений в состоянии участников тренинга.
13. Алгоритм использования критерия знаков G
АЛГОРИТМ ИСПОЛЬЗОВАНИЯ КРИТЕРИЯЗНАКОВ G
1.Определить величину сдвига, как разность между соответствующими
значениями показателя после и до эксперимента.
2.Подсчитать количество положительных и отрицательных сдвигов.
3. Сумму чисел, найденных в п.2 использовать для определения
критических значений показателя.
4. Построить ось значимости (направление оси - справа налево).
5. Наименьшее значение чисел, найденных в п.2 (нетипичный сдвиг)
обозначить как Gэмп и нанести его на ось значимости.
6. Сделать вывод о принятии нулевой или альтернативной гипотез.
7. Интерпретировать задачу.
14. Для применения критерия знаков G необходимо соблюдать следующие условия:
ДЛЯ ПРИМЕНЕНИЯ КРИТЕРИЯ ЗНАКОВ GНЕОБХОДИМО СОБЛЮДАТЬ СЛЕДУЮЩИЕ
УСЛОВИЯ:
1. Измерение может быть проведено в шкале порядка,
интервалов или отношений.
2. Выборка должна быть однородной и связной.
3. Число элементов в сравниваемых выборках должно
быть равным.
4. Критерий знаков G может применяться при величине
типичного сдвига от 5 до 300 (на большую величину не
рассчитана таблица достоверности).
5. При большом числе сравниваемых парных значений
критерий знаков достаточно эффективен.
6. При равенстве типичных и нетипичных сдвигов
критерий знаков неприменим, следует использовать
другие критерии.
15. Парный критерий Т - Вилкоксона
ПАРНЫЙ КРИТЕРИЙ Т - ВИЛКОКСОНАКритерий является более мощным, чем критерий
знаков, и применяется для оценки различий
экспериментальных данных, полученных в двух
разных условиях на одной и той же выборке
испытуемых. Он позволяет выявить не только
направленность изменений, но и их выраженность,
т.е. он позволяет установить, насколько сдвиг
показателей в каком-то одном направлении является
более интенсивным, чем в другом.
Настоящий статистический метод был
предложен Фрэнком Вилкоксоном в 1945 году.
16.
Задача. Психолог проводит с младшими школьникамикоррекционную работу по формированию навыков
внимания, используя для оценки результатов корректурную
пробу. Задача состоит в том, чтобы определить будет ли
уменьшаться количество ошибок внимания у младших
школьников после специальных коррекционных упражнений.
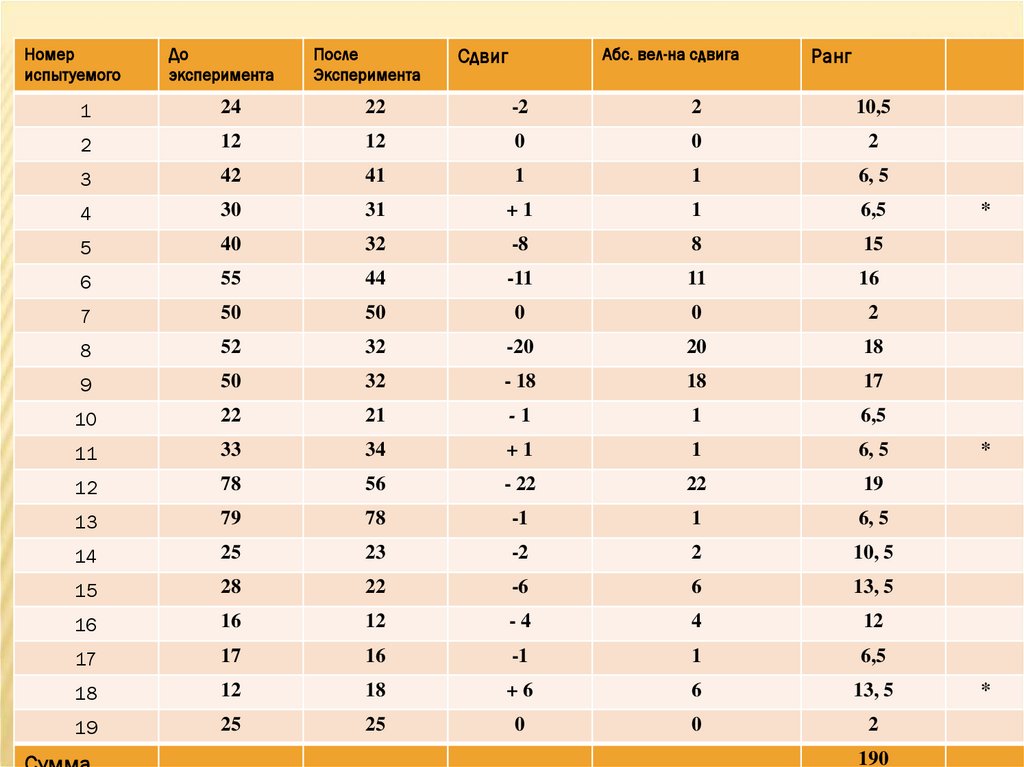
Решение: Для решения этой задачи психолог у 19 детей
определяет количество ошибок при выполнении
корректурной пробы до и после коррекционных упражнений.
В таблице приведены соответствующие экспериментальные
данные.
17.
Номериспытуемого
До
эксперимента
После
Эксперимента
Абс. вел-на сдвига
1
24
22
-2
2
10,5
2
12
12
0
0
2
3
42
41
1
1
6, 5
4
30
31
+1
1
6,5
5
40
32
-8
8
15
6
55
44
-11
11
16
7
50
50
0
0
2
8
52
32
-20
20
18
9
50
32
- 18
18
17
10
22
21
-1
1
6,5
11
33
34
+1
1
6, 5
12
78
56
- 22
22
19
13
79
78
-1
1
6, 5
14
25
23
-2
2
10, 5
15
28
22
-6
6
13, 5
16
16
12
-4
4
12
17
17
16
-1
1
6,5
18
12
18
+6
6
13, 5
19
25
25
0
0
2
Сдвиг
Ранг
190
*
*
*
18.
Проверка правильности ранжирования:(19*20)/2=190
Количество нетипичных сдвигов – 3 (в таблице
отмечены звездочкой)
Эмпирическое значение
определяется как сумма рангов
нетипичных сдвигов
Тэмп = 6,5 + 13,5 + 6,5 = 26,5
Критическое значение
определяется по таблице для n = 19
19.
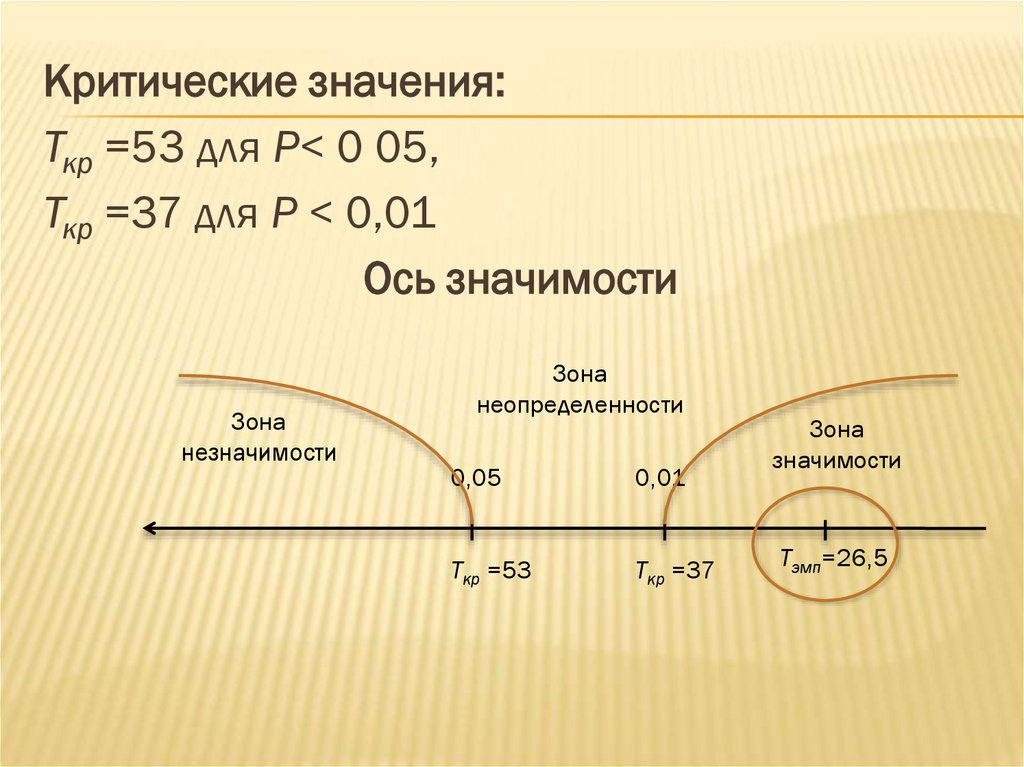
Критические значения:Ткр =53 для Р< 0 05,
Ткр =37 для Р < 0,01
Ось значимости
Зона
незначимости
Зона
неопределенности
0,05
0,01
Tкр =53
Tкр =37
Зона
значимости
Tэмп=26,5
20.
Величина Тэмп попадает в зону значимости.Можно утверждать, что зафиксированные в
эксперименте
изменения
неслучайны
и
значимы на 1% уровне. Таким образом,
применение
коррекционных
упражнений
способствует повышению точности выполнения
корректурной пробы.
Полученный
результат
может
быть
переформулирован в терминах нулевой и
альтернативной
гипотез,
поскольку
преобладание
типичного
отрицательного
направления сдвига в данном конкретном
эксперименте не является случайным, то должна
быть принята гипотеза Н1 о наличии различий, а
гипотеза H0 отклонена.
21. Алгоритм использования критерия Т-Вилкоксона
АЛГОРИТМ ИСПОЛЬЗОВАНИЯ КРИТЕРИЯ ТВИЛКОКСОНА1.Определить величину сдвига, как разность между
соответствующими значениями показателя после и до
эксперимента.
2.Найти абсолютную величину сдвига.
3. Проранжировать абсолютную величину сдвига.
4.Определить нетипичный сдвиг и найти сумму рангов,
соответствующих значениям нетипичного сдвига.
Обозначить найденную сумму Тэмп.
5. По соответствующей таблице определить критические
значения параметра в зависимости от объема выборки.
6. Построить ось значимости и нанести на нее все данные
(направление оси - справа налево).
7. Сделать вывод о принятии нулевой или альтернативной
гипотез.
8. Интерпретировать задачу.
22. Для применения критерия Т-Вилкоксона необходимо соблюдать следующие условия:
ДЛЯ ПРИМЕНЕНИЯ КРИТЕРИЯ Т-ВИЛКОКСОНАНЕОБХОДИМО СОБЛЮДАТЬ СЛЕДУЮЩИЕ
УСЛОВИЯ:
1. Измерение может быть проведено во всех
шкалах, кроме номинальной.
2. Выборка должна быть связной.
3. Число элементов в сравниваемых выборках
должно быть равным.
4. Критерий Т— Вилкоксона может применяться
при численности выборки от 5 до 50 (на
большую величину не рассчитана таблица
достоверности).
23. Критерий Фридмана
КРИТЕРИЙ ФРИДМАНАКритерий Фридмана можно рассматривать
как распространение критерия Т—
Вилкоксона на три и большее количество
измерений связной выборки испытуемых.
Критерий позволяет установить уровень
статистической достоверности различий сразу
в нескольких измерениях (от 3 до 100), но не
дает возможности выявить направление
изменений (для этого используется критерий
Пейджа).
24.
Задача. Шести школьникам предъявляют тестРавена. Фиксируется время решения
каждого задания. Выясняется вопрос — будут
ли найдены статистически значимые
различия между временем решения первых
трех заданий теста?
Решение: психолог измерил время решения
первых трех задании теста у шести
испытуемых. Результаты этих измерении
приведены в таблице.
25.
№ испытуемыхп/п
Время решения Время решения Время решения
первого задания в второго задания в третьего задания
секундах
секундах
в секундах
1
8
3
5
2
4
15
12
3
6
23
15
4
3
6
6
5
7
12
3
6
15
24
12
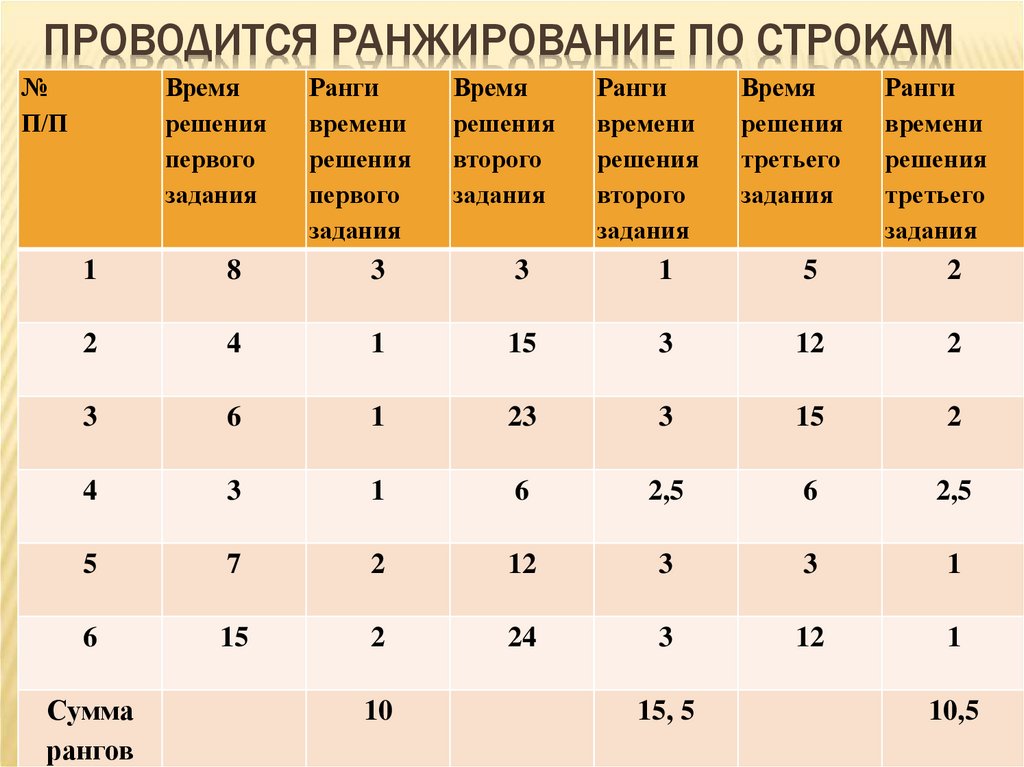
26. Проводится ранжирование по строкам
ПРОВОДИТСЯ РАНЖИРОВАНИЕ ПО СТРОКАМ№
П/П
Время
решения
первого
задания
Ранги
времени
решения
первого
задания
Время
решения
второго
задания
Ранги
времени
решения
второго
задания
Время
решения
третьего
задания
Ранги
времени
решения
третьего
задания
1
8
3
3
1
5
2
2
4
1
15
3
12
2
3
6
1
23
3
15
2
4
3
1
6
2,5
6
2,5
5
7
2
12
3
3
1
6
15
2
24
3
12
1
Сумма
рангов
10
15, 5
10,5
27.
Проверка правильности ранжирования:n*c*(c + 1)/2=6* 3* (3 + 1)/2=36
Сумма рангов: 10 + 15,5 + 10,5 = 36
Расчет эмпирического значения критерия
Фридмана, осуществляемый по следующей
формуле:
n - количество испытуемых (строк),
с — количество столбцов,
Ri — сумма рангов i-того столбца.
28.
Критические значения:X2кр=6,33 для Р< 0,052,
X2кр=8,33 для Р < 0,012
Ось значимости
Зона
незначимости
X2фр=3,08
Зона
неопределенности
0,05
0,01
X2кр=6,33
X2кр=8,33
Зона
значимости
29.
Полученное эмпирическое значение критерияФридмана попало в зону незначимости. Отсюда
следует, что статистически значимых различий во
времени решения первых трех заданий теста нет.
Полученный
результат
может
быть
переформулирован в терминах нулевой и
альтернативной
гипотез:
поскольку
между
показателями, измеренными в трех разных
условиях, существуют лишь случайные различия,
то принимается нулевая гипотеза Но, т. е. гипотеза
о сходстве, а гипотеза Н1 отклоняется.
30. Алгоритм использования критерия Фридмана
АЛГОРИТМ ИСПОЛЬЗОВАНИЯ КРИТЕРИЯФРИДМАНА
1.Провести ранжирование по всем показателям для
каждого испытуемого.
2.Найти сумму рангов, соответствующих каждому
показателю.
3. Рассчитать эмпирическое значение критерия по
формуле.
4. По соответствующей таблице определить
критические значения параметра в зависимости от
объема выборки.
5. Построить ось значимости и нанести на нее все
данные.
6. Сделать вывод о принятии нулевой или
альтернативной гипотез.
7. Интерпретировать задачу.
31.
Для применения критерия Фридмананеобходимо соблюдать следующие
условия:
1. Измерение должно быть проведено в шкале
интервалов или отношений.
2. Выборка должна быть связной.
3. В выборке должно быть не менее двух испытуемых,
каждый из которых имеет не менее трех измеренных
показателей. Верхний предел для количества
испытуемых не определен, а количество измерений
не может превышать 100.
4. В зависимости от числа измерений и количества
испытуемых используются разные таблицы
значимости.
32. Правила использования таблиц для нахождения критических значений
ПРАВИЛА ИСПОЛЬЗОВАНИЯ ТАБЛИЦ ДЛЯНАХОЖДЕНИЯ КРИТИЧЕСКИХ ЗНАЧЕНИЙ
1. При общем количестве измерений равном 3 и числе
испытуемых от 2 до 9 критические значения критерия
Фридмана определяются по таблице 3 Приложения.
2. При общем количестве измерений равном 4 и числе
испытуемых от 2 до 4 критические значения критерия
Фридмана определяются по таблице 4 Приложения.
3. При большем количестве измерении и испытуемых
критические значения критерия Фридмана определяются
по таблице 12 Приложения для критерия хи-квадрат. В
этом случае число степеней свободы определяется по
формуле v =с-1. где с — количество условий измерения.
(По учебнику «Математическая статистика для психологов»
О.Ю. Ермолаев)
33. Критерий L тенденций Пейджа
КРИТЕРИЙ L ТЕНДЕНЦИЙ ПЕЙДЖАЕсли предыдущей критерий позволяет только
выявлять различия между выборками, то
критерий Педжа выявляет тенденцию, т.е.
направление в изменение величин.
34. Критерий L тенденций Пейджа
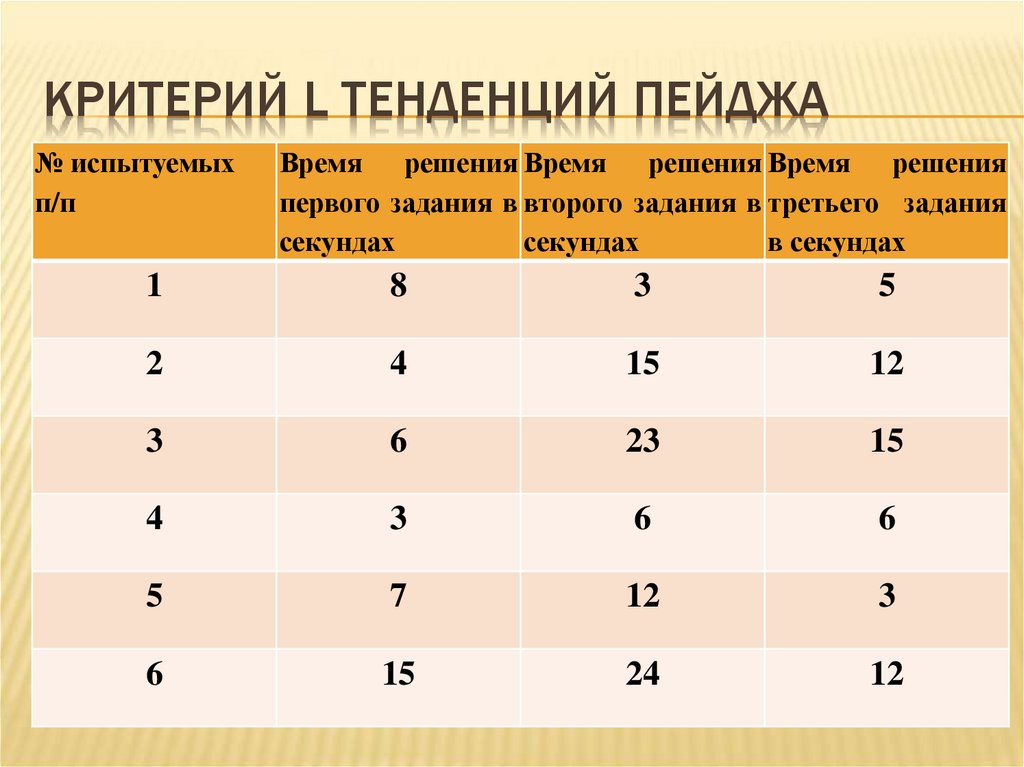
КРИТЕРИЙ L ТЕНДЕНЦИЙ ПЕЙДЖАЗадача. Шести школьникам предъявляют тест
Равена. Фиксируется время решения
каждого задания. Выясняется вопрос — будут
ли найдены статистически значимые
различия между временем решения первых
трех заданий теста и можно ли выявить
тенденцию во времени решения?
Решение: психолог измерил время решения
первых трех задании теста у шести
испытуемых. Результаты этих измерении
приведены в таблице.
35. Критерий L тенденций Пейджа
КРИТЕРИЙ L ТЕНДЕНЦИЙ ПЕЙДЖА№ испытуемых
п/п
Время решения Время решения Время решения
первого задания в второго задания в третьего задания
секундах
секундах
в секундах
1
8
3
5
2
4
15
12
3
6
23
15
4
3
6
6
5
7
12
3
6
15
24
12
36. Критерий L тенденций Пейджа
КРИТЕРИЙ L ТЕНДЕНЦИЙ ПЕЙДЖАУточнение вопроса задачи:
Проверить тенденцию, что время решения
второй задачи выше, чем время решения
первой и третьей.
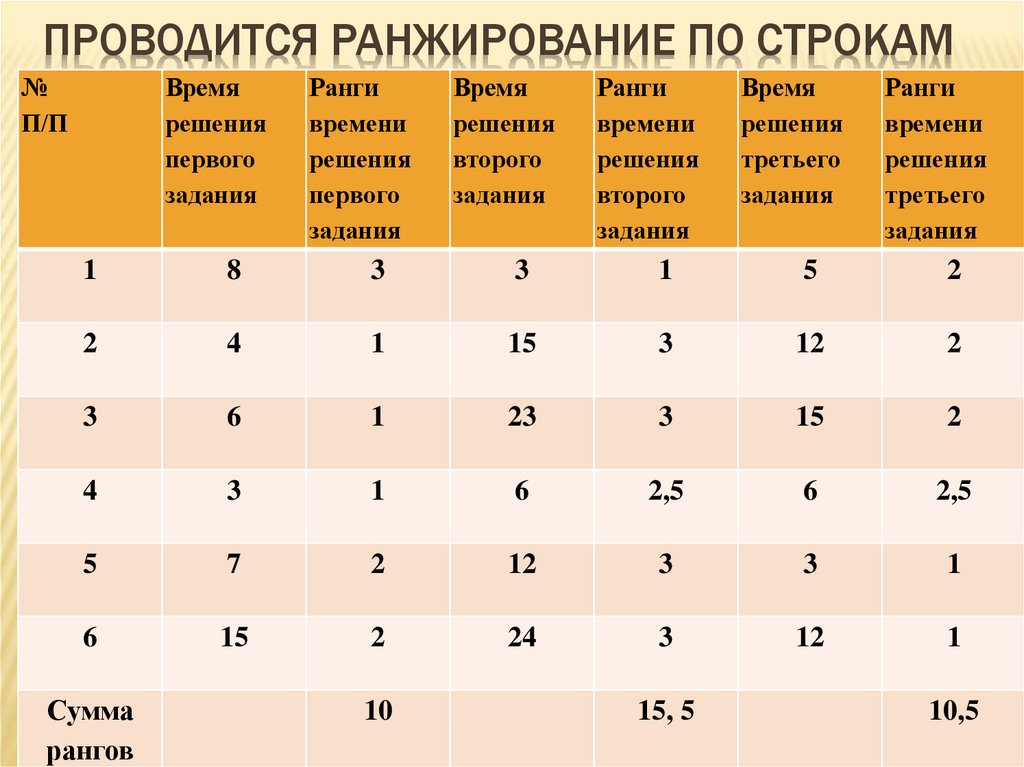
37. Проводится ранжирование по строкам
ПРОВОДИТСЯ РАНЖИРОВАНИЕ ПО СТРОКАМ№
П/П
Время
решения
первого
задания
Ранги
времени
решения
первого
задания
Время
решения
второго
задания
Ранги
времени
решения
второго
задания
Время
решения
третьего
задания
Ранги
времени
решения
третьего
задания
1
8
3
3
1
5
2
2
4
1
15
3
12
2
3
6
1
23
3
15
2
4
3
1
6
2,5
6
2,5
5
7
2
12
3
3
1
6
15
2
24
3
12
1
Сумма
рангов
10
15, 5
10,5
38. Критерий L тенденций Пейджа
КРИТЕРИЙ L ТЕНДЕНЦИЙ ПЕЙДЖАРасчетная формула:
c
Lэмп ( Ri i )
i 1
Ri — сумма рангов i-того столбца (суммы
выстраиваются по возрастанию).
i- порядковый номер в упорядоченном ряду
сумм.
39. Критерий L тенденций Пейджа
КРИТЕРИЙ L ТЕНДЕНЦИЙ ПЕЙДЖАLэмп 1 10 2 10,5 3 15,5 87,5
Критические значения:
Lкр =79 для Р< 0 05,
Lкр =81 для Р < 0,01
Зона
незначимости
Зона
неопределенности
0,05
0,01
Зона
значимости
Lкр=79
Lэмп =87,5
Lкр=81
40.
Полученное эмпирическое значение критерия Пейджапопало в зону значимости. Отсюда следует, что выявлены
статистически значимые различия во времени решения
первых трех заданий теста и можно подтвердить тенденцию о
том, что время решения второго задания больше, чем время
решения первого и третьего.
Полученный результат может быть переформулирован в
терминах нулевой и альтернативной гипотез: поскольку
между показателями, измеренными в трех разных условиях,
существуют неслучайные различия, то принимается гипотеза
Н1, т. е. гипотеза о различии, а гипотеза Н0 отклоняется.
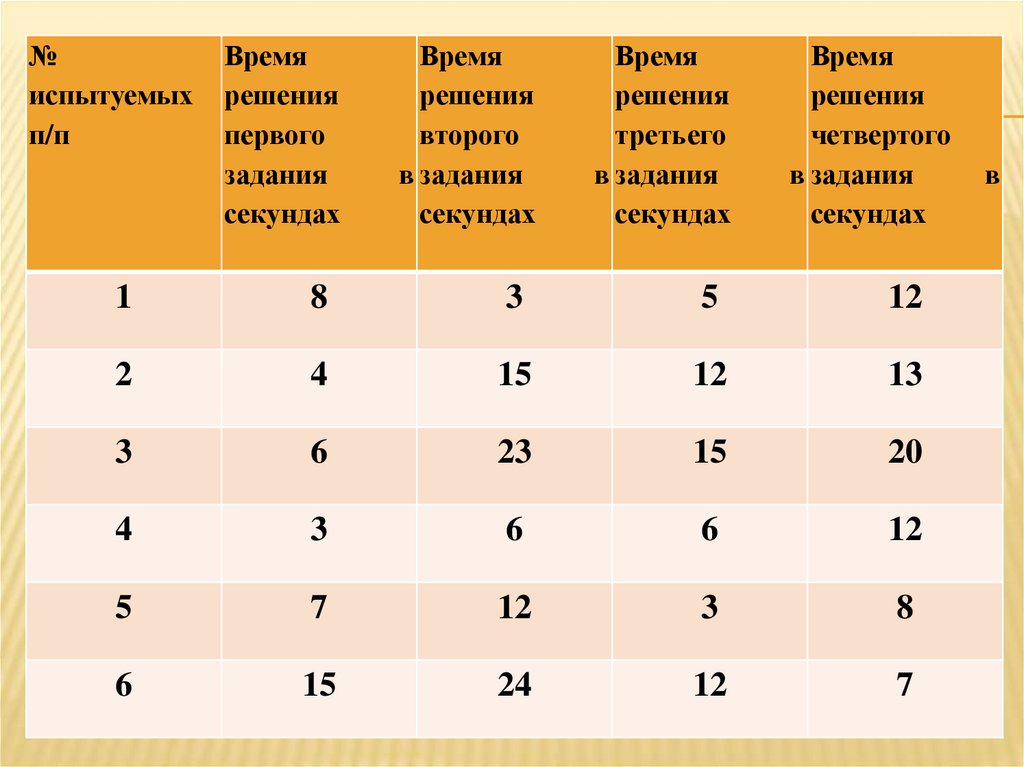
41.
№испытуемых
п/п
Время
решения
первого
задания
секундах
Время
решения
второго
в задания
секундах
Время
решения
третьего
в задания
секундах
Время
решения
четвертого
в задания
секундах
1
8
3
5
12
2
4
15
12
13
3
6
23
15
20
4
3
6
6
12
5
7
12
3
8
6
15
24
12
7
КРИТЕРИЙ L ТЕНДЕНЦИЙ ПЕЙДЖА
в
42. Критерий L тенденций Пейджа
КРИТЕРИЙ L ТЕНДЕНЦИЙ ПЕЙДЖАУсловия применимости критерия:
1. Измерение должно быть проведено в шкале рангов,
интервалов или отношений.
2. Выборка должна быть связной.
3. В выборке должно быть не менее двух и не больше 12
испытуемых, каждый из которых имеет не менее трех
измеренных показателей.




































 Математика
Математика








