Похожие презентации:
Квадратные уравнения
1.
Квадратныеуравнения
2.
Квадратным уравнением называетсяуравнение вида ах2 + вх +с = 0,
где х –переменная,
а, в и с - некоторые числа,
причем а 0.
3.
Квадратное уравнение называютприведенным, если его старший
коэффициент равен 1.
Квадратное уравнение называют не
приведенным, если его старший
коэффициент отличен от 1.
4.
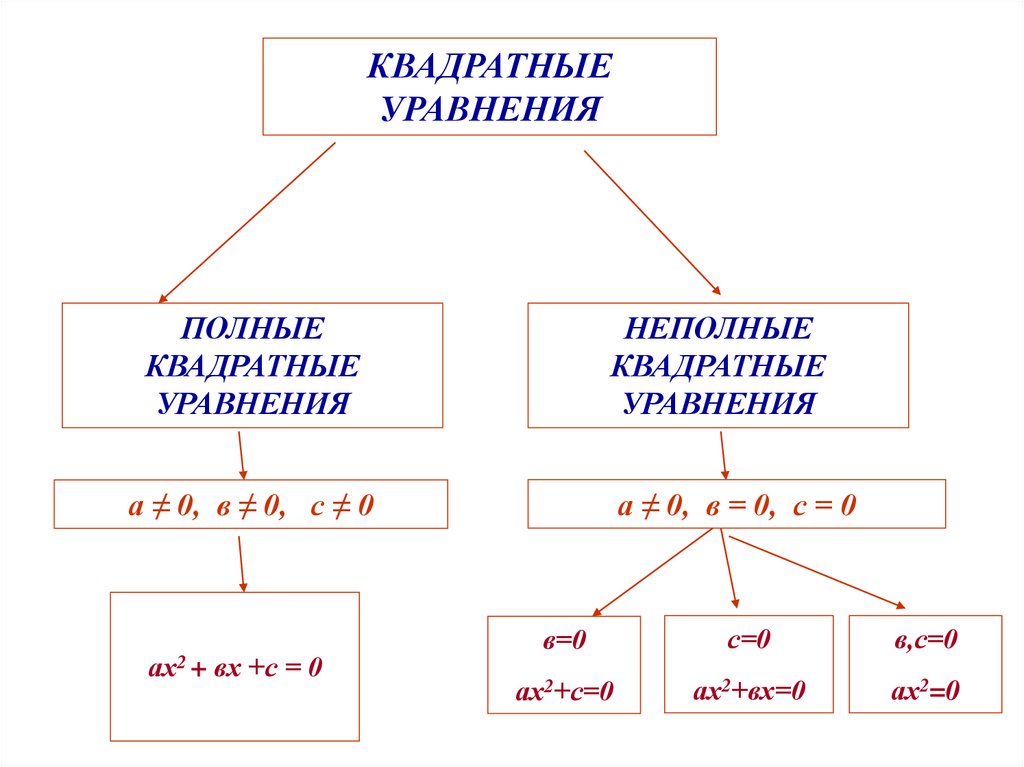
КВАДРАТНЫЕУРАВНЕНИЯ
ПОЛНЫЕ
КВАДРАТНЫЕ
УРАВНЕНИЯ
НЕПОЛНЫЕ
КВАДРАТНЫЕ
УРАВНЕНИЯ
а ≠ 0, в ≠ 0, с ≠ 0
а ≠ 0, в = 0, с = 0
ах2 + вх +с = 0
в=0
с=0
в,с=0
ах2+с=0
ах2+вх=0
ах2=0
5.
Корнем квадратного уравнения ах2 + вх +с = 0называют всякое значение переменной х, при котором
квадратный трехчлен ах2 + вх +с обращается в нуль;
такое значение переменной х называют также корнем
квадратного трехчлена.
Можно сказать и так:
корень квадратного уравнения ах2 + вх +с = 0 - это
такое значение х, подстановка которого в уравнение
обращает уравнение в верное числовое равенство
0 = 0.
Решить квадратное уравнение — значит найти все его
корни или установить, что корней нет.
6.
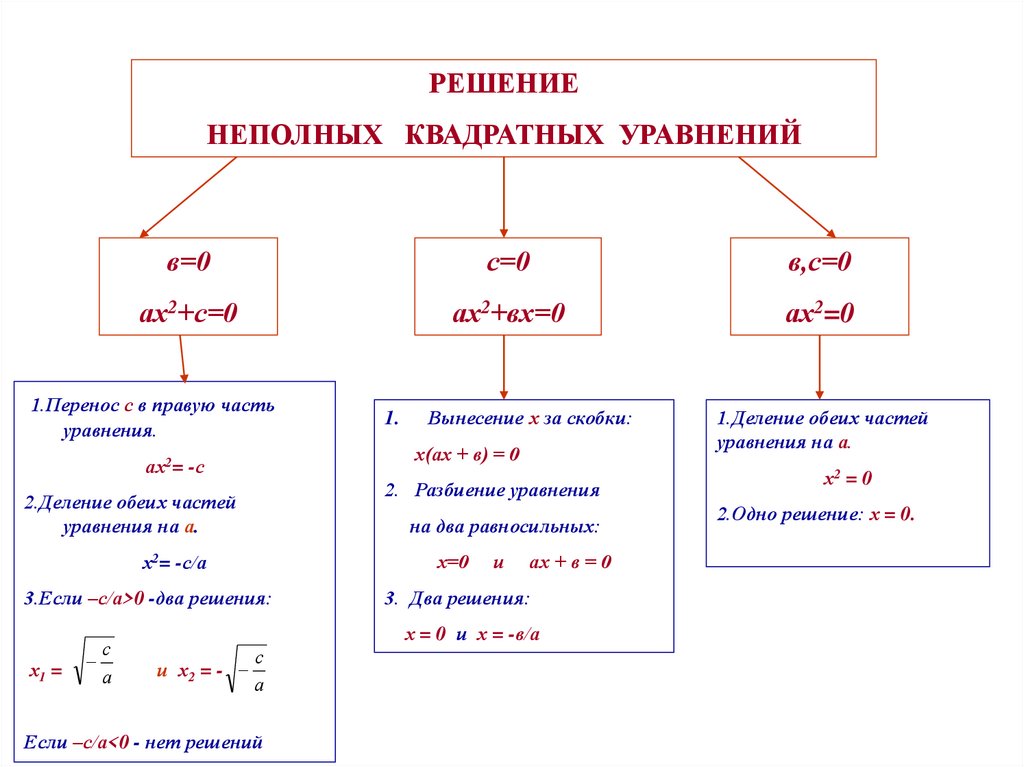
РЕШЕНИЕНЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0
с=0
в,с=0
ах2+с=0
ах2+вх=0
ах2=0
1.Перенос с в правую часть
уравнения.
2. Разбиение уравнения
2.Деление обеих частей
уравнения на а.
на два равносильных:
х=0
х2= -с/а
3.Если –с/а>0 -два решения:
х1 =
Вынесение х за скобки:
х(ах + в) = 0
ах2= -с
с
а
1.
и
ах + в = 0
3. Два решения:
х = 0 и х = -в/а
и х2 = -
с
а
Если –с/а<0 - нет решений
1.Деление обеих частей
уравнения на а.
х2 = 0
2.Одно решение: х = 0.
7.
Способы решенияполных квадратных уравнений
1. Выделение квадрата двучлена.
1.
Формула: D = b2- 4ac,
2. График.
3. Теорема Виета.
b D
x1,2=
2a
8.
Формула корней квадратного уравнения9.
Основные теоремы10.
11.
Решить уравнение12.
Решить уравнение13.
Решить уравнение14.
15.
Решите уравнения с помощью формул1 вариант:
а) -7х + 5х2 + 1 =0
б) (х – 1)(х + 1) = 2 (5х – 10,5)
2 вариант:
а) 2х2 + 5х -7 = 0
б) –х2 = 5х - 14
3 вариант:
а) х2 – 8х + 7 = 0
б) 6х – 9 = х2
16.
От чего зависит количество корней квадратногоуравнения?











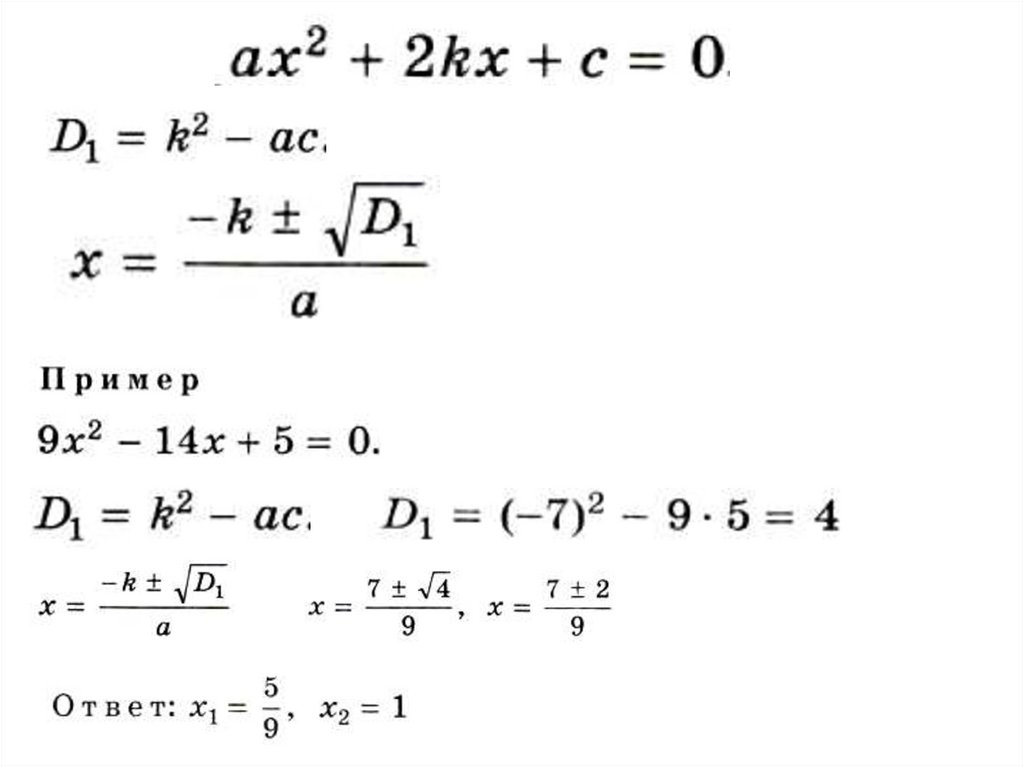


 Математика
Математика








