Похожие презентации:
Теория и практика по заданию 11 материалов ОГЭ
1.
ГБОУ Школа №543 Московского районаСанкт-Петербурга
«Теория и практика
по заданию 11
материалов ОГЭ»
Учитель математики
высшей категории
Чагина Юлия
Анатольевна
2.
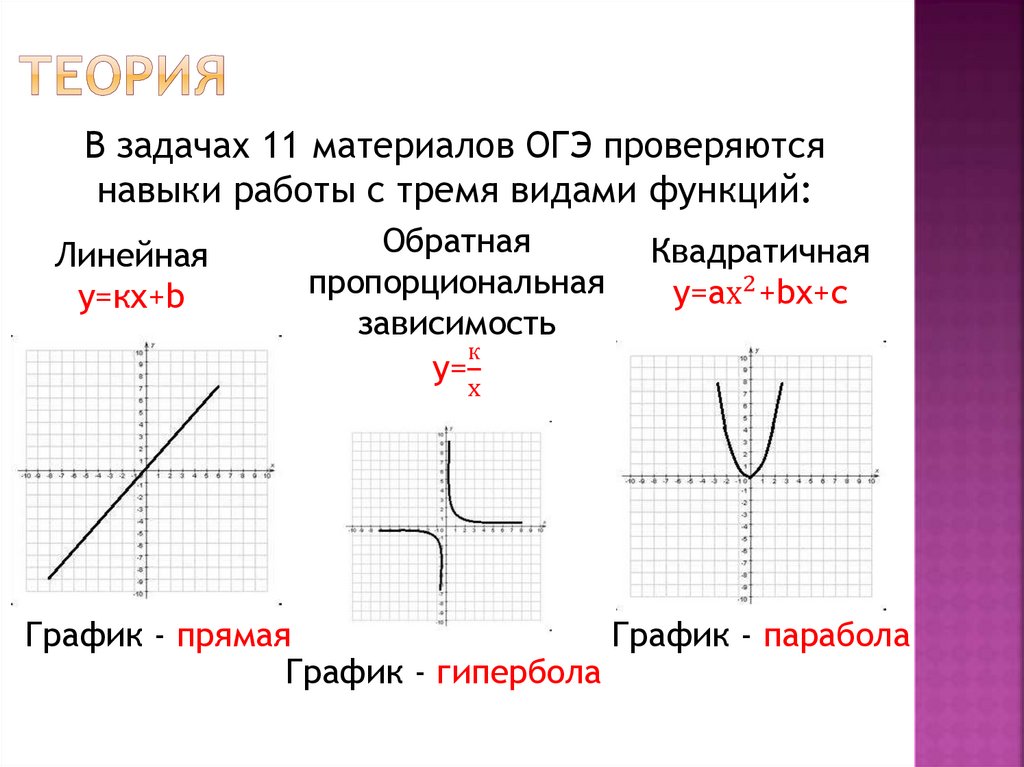
В задачах 11 материалов ОГЭ проверяютсянавыки работы с тремя видами функций:
Линейная
у=кх+b
Обратная
пропорциональная
зависимость
к
у=
Квадратичная
у=ах2 +bх+с
х
График - прямая
График - парабола
График - гипербола
3.
Задаетсяуравнением вида у=кх+b. Графиком
функции является прямая. Коэффициенты к и b
определяют
расположение
прямой
на
координатной плоскости.
4.
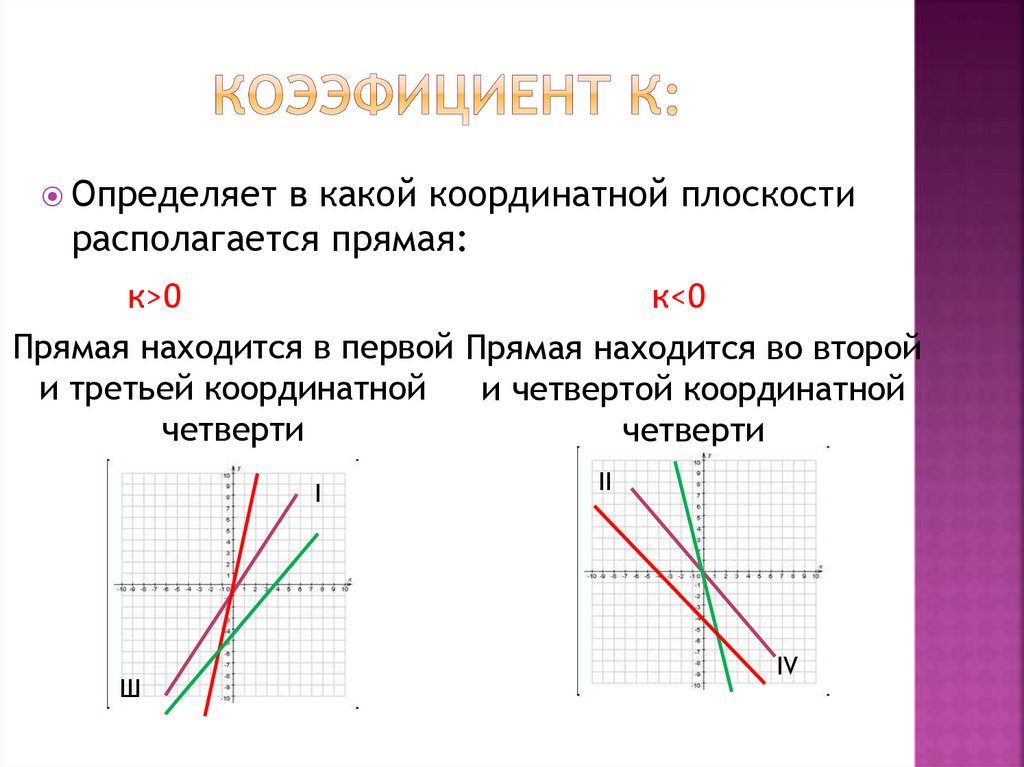
Определяет в какой координатной плоскостирасполагается прямая:
к>0
к<0
Прямая находится в первой Прямая находится во второй
и третьей координатной
и четвертой координатной
четверти
четверти
I
Ш
II
IV
5.
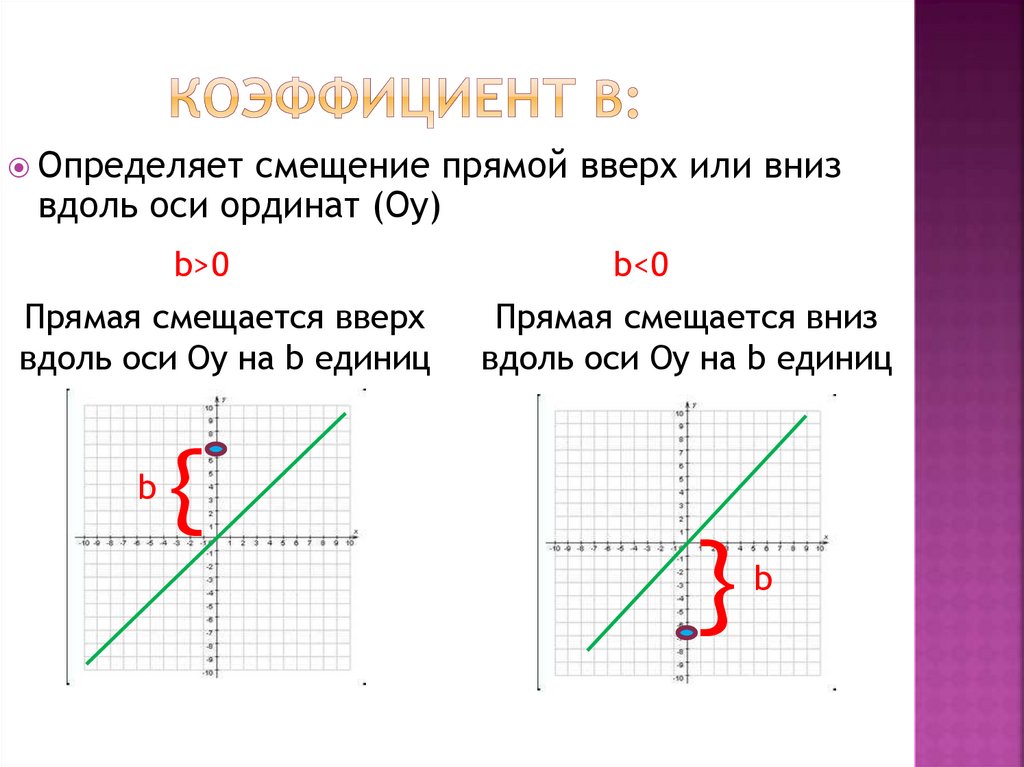
Определяет смещение прямой вверх или внизвдоль оси ординат (Оу)
b>0
Прямая смещается вверх
вдоль оси Оу на b единиц
b
{
b<0
Прямая смещается вниз
вдоль оси Оу на b единиц
}
b
6.
Ib
III
{
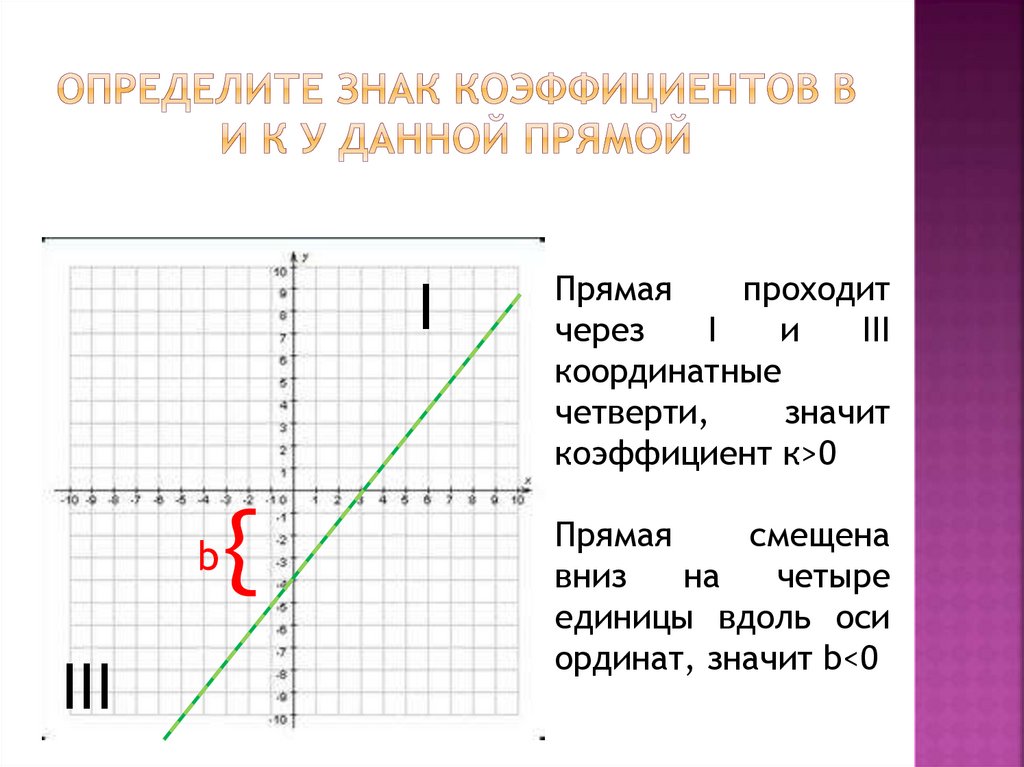
Прямая
проходит
через
I
и
III
координатные
четверти,
значит
коэффициент к>0
Прямая
смещена
вниз
на
четыре
единицы вдоль оси
ординат, значит b<0
7.
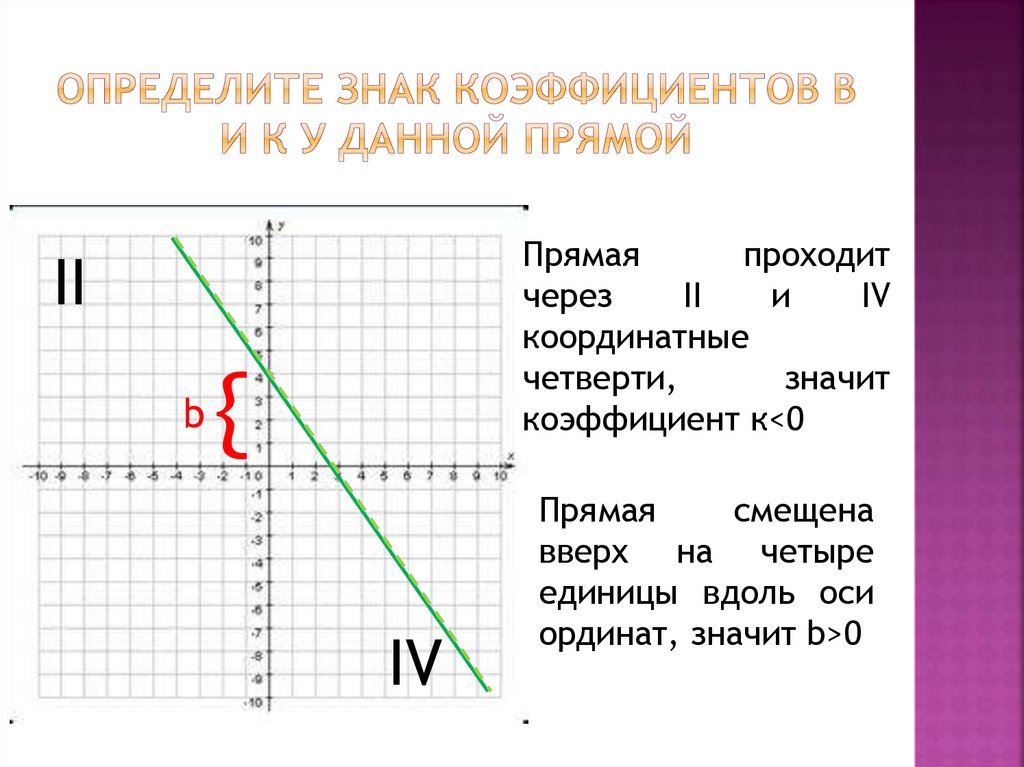
Прямаяпроходит
через
II
и
IV
координатные
четверти,
значит
коэффициент к<0
II
b
{
IV
Прямая
смещена
вверх на четыре
единицы вдоль оси
ординат, значит b>0
8.
Задается уравнением вида у=ах +bх+с2
Графиком
функции
является
парабола.
Коэффициенты а, b и с определяют расположение
прямой на координатной плоскости.
9.
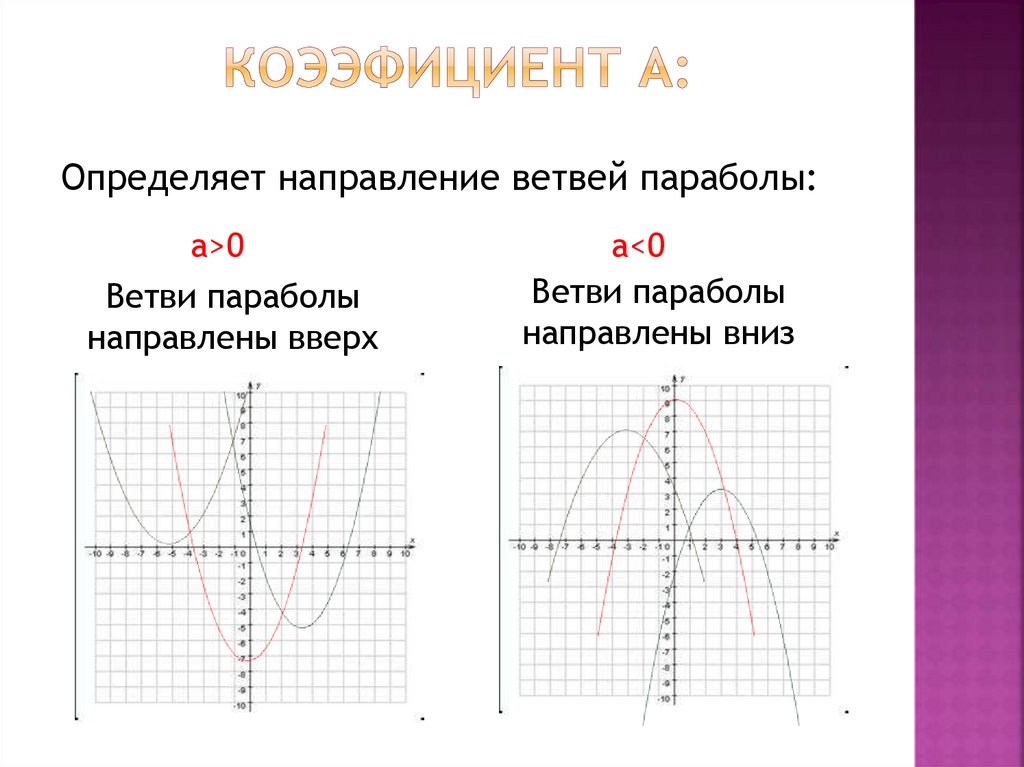
Определяет направление ветвей параболы:а>0
Ветви параболы
направлены вверх
а<0
Ветви параболы
направлены вниз
10.
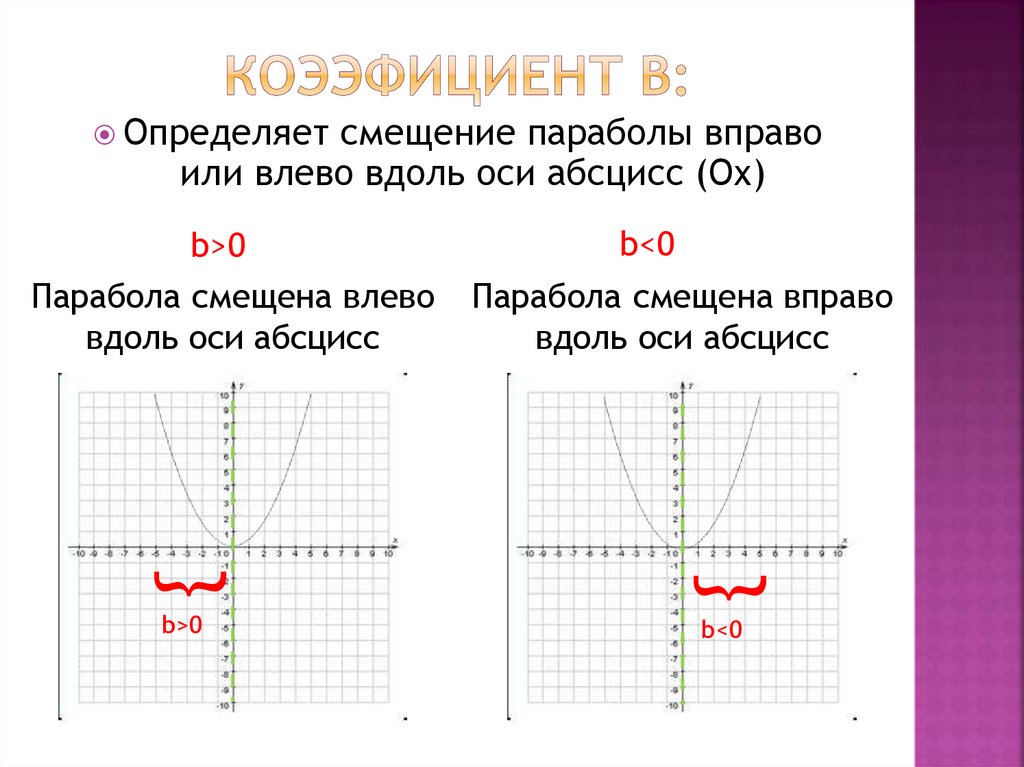
Определяет смещение параболы вправоили влево вдоль оси абсцисс (Ох)
b<0
{
Парабола смещена вправо
вдоль оси абсцисс
{
b>0
Парабола смещена влево
вдоль оси абсцисс
b>0
b<0
11.
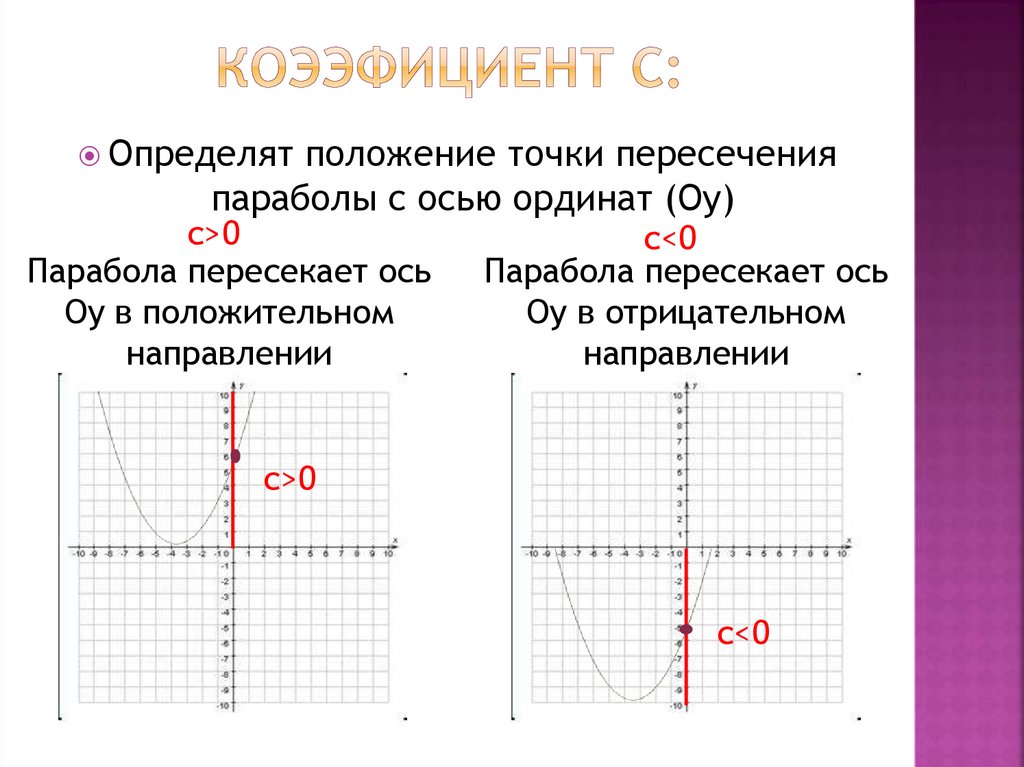
Определят положение точки пересеченияпараболы с осью ординат (Оу)
с>0
Парабола пересекает ось
Оу в положительном
направлении
с<0
Парабола пересекает ось
Оу в отрицательном
направлении
с>0
с<0
12.
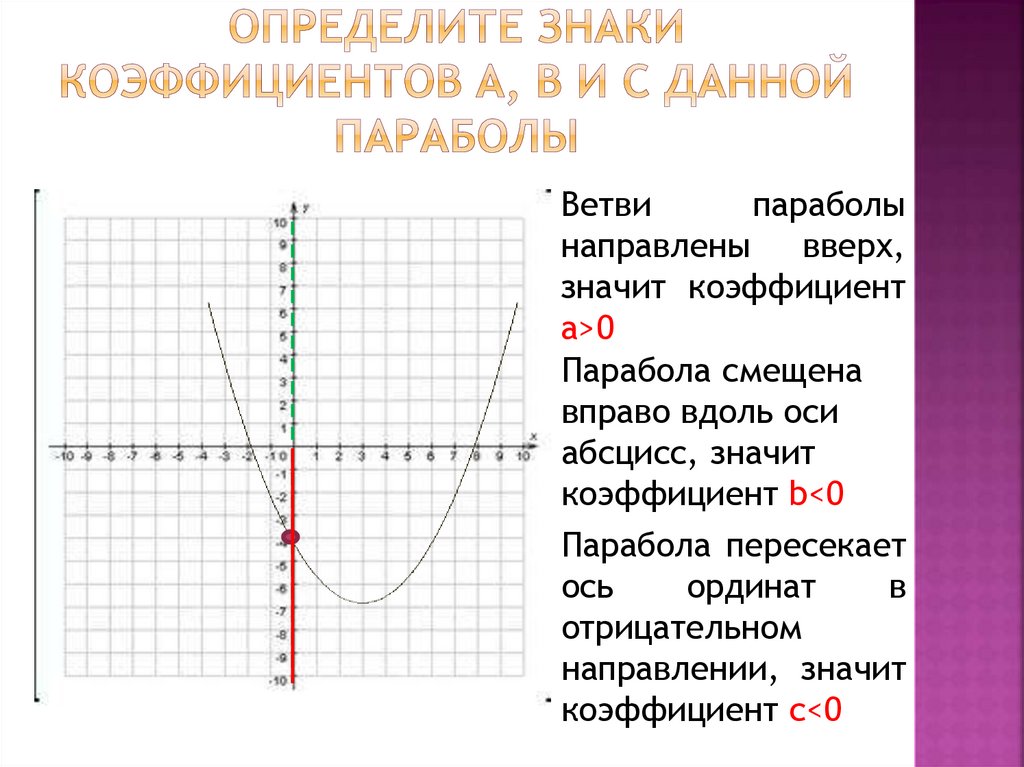
Ветвипараболы
направлены
вверх,
значит коэффициент
а>0
Парабола смещена
вправо вдоль оси
абсцисс, значит
коэффициент b<0
Парабола пересекает
ось
ординат
в
отрицательном
направлении, значит
коэффициент с<0
13.
12
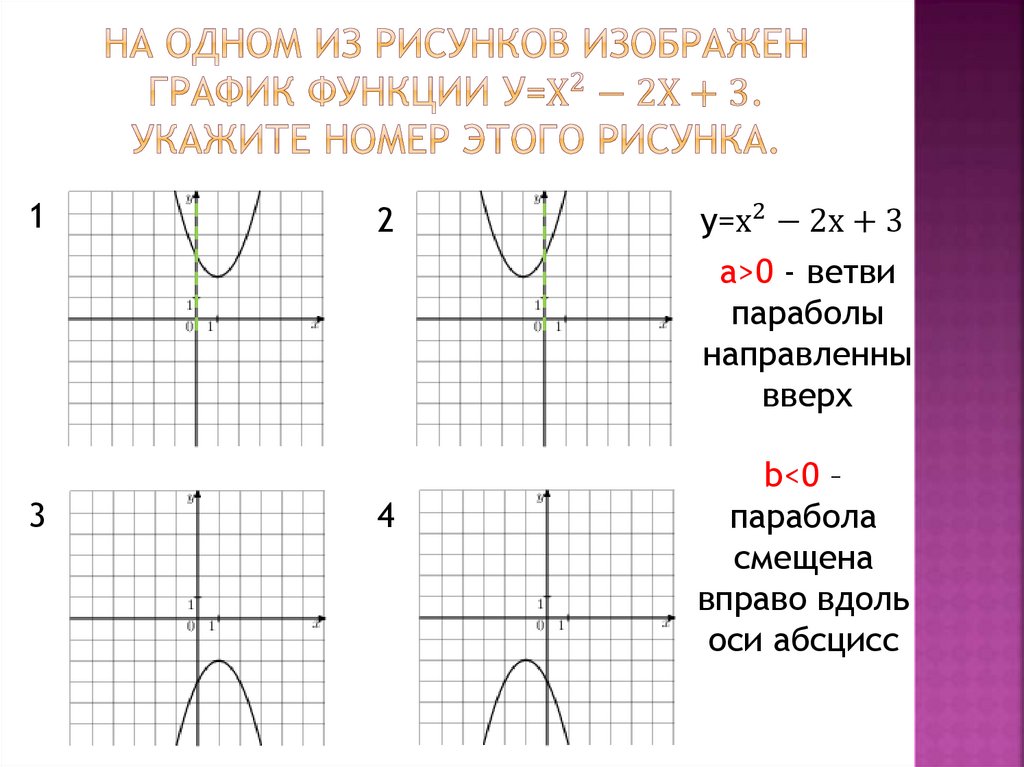
у=х2 − 2х + 3
а>0 - ветви
параболы
направленны
вверх
3
4
b<0 –
парабола
смещена
вправо вдоль
оси абсцисс
14.
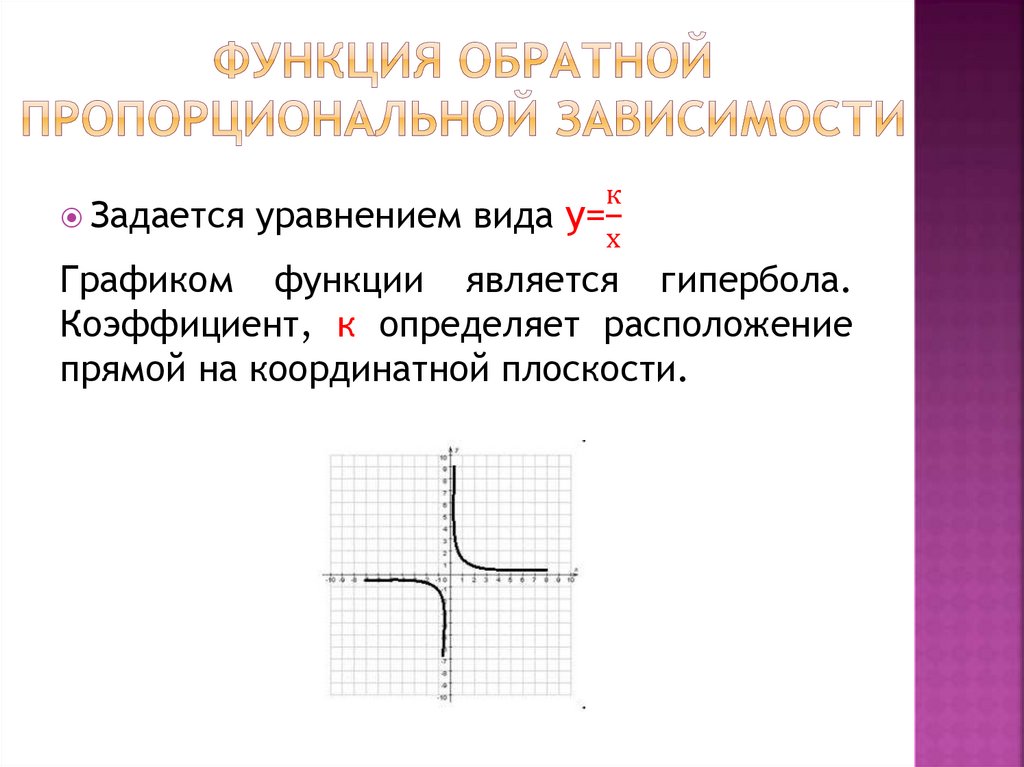
кЗадается уравнением вида у=
х
Графиком функции является гипербола.
Коэффициент, к определяет расположение
прямой на координатной плоскости.
15.
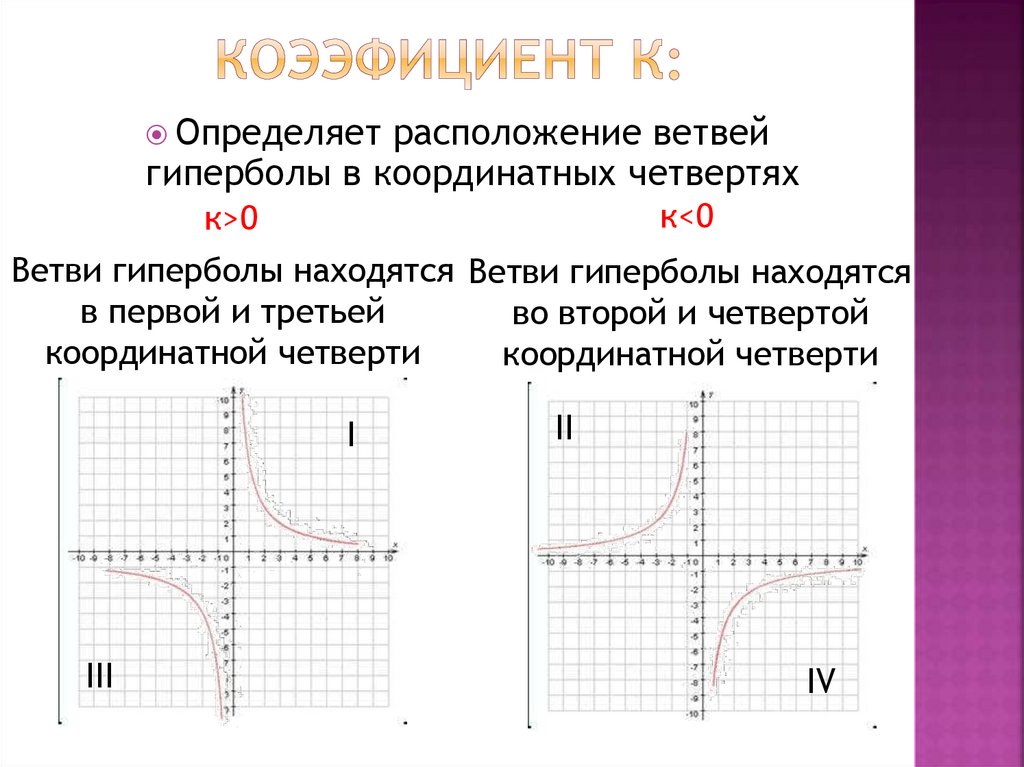
Определяет расположение ветвейгиперболы в координатных четвертях
к<0
к>0
Ветви гиперболы находятся Ветви гиперболы находятся
в первой и третьей
во второй и четвертой
координатной четверти
координатной четверти
I
III
II
IV




 Математика
Математика








