Похожие презентации:
Поверхности второго порядка
1.
Поверхности второго порядка2.
ОпределениеУравнением поверхности в некоторой
аффинной системе координат в
пространстве называется уравнение вида,
F x, y, z 0
которому удовлетворяют координаты
любой точки поверхности и не
удовлетворяют координаты ни одной
точки, не принадлежащей этой
поверхности
3.
Поверхностью второго порядканазывается множество всех точек пространства,
координаты которых в какой-либо аффинной
системе координат удовлетворяют уравнению
второй степени
a11x2+a22y2+a33z2+2a12xy+2a13xz+
+2a23yz+2a10x+2a20y+2a30z+a00=0 ,
где не все коэффициенты при членах второй
степени равны нулю.
4.
не вырожденные поверхности• эллипсоиды,
• гиперболоиды,
• параболоиды,
• конусы
• цилиндры.
5.
Будем рассматривать основные типыповерхностей, используя их простейшие
канонические уравнения.
Для изучения формы поверхности применим
метод сечений.
Пусть поверхность S задана в прямоугольной
системе координат. Пересечем поверхность
плоскостями, параллельными координатным
плоскостям (или самими координатными
плоскостями), и найдем линии пересечения
поверхности с этими плоскостями.
По виду этих линий и выносится суждение о
форме поверхности S.
6. Эллипсоид
ОпределениеЭллипсоидом называется поверхность второго
порядка, которая в некоторой прямоугольной
системе координат определяется уравнением
2
2
2
x
y
z
2 2 1
2
a
b
c
7. ИССЛЕДОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ЭЛЛИПСОИДА
1)Сечения плоскостями x = h:
x2 y2 z 2
2 2 2 1,
a
b
c
x h .
y2 z2
h2
2 1 2 .
2
b
c
a
Это уравнение определяет
а) при | h | < a – эллипс (причем, чем больше | h |,
тем меньше полуоси эллипса);
б) при | h | = a – точку A2,1( a; 0; 0);
в) при | h | > a – мнимую кривую.
8.
3) Сечения плоскостями y = h:x2 y2 z 2
2 2 2 1,
a
b
c
y h .
2
2
2
x z
h
2 2 1 2 .
a c
b
Это уравнение определяет
а) при | h | < b – эллипс (причем, чем больше | h |,
тем меньше полуоси эллипса);
б) при | h | = b – точку B2,1(0; b; 0);
в) при | h | > b – мнимую кривую.
9.
3) Сечения плоскостями z = h:x2 y2 z 2
2 2 2 1,
a
b
c
z h .
2
2
2
x y
h
2 2 1 2 .
a b
c
Это уравнение определяет
а) при | h | < c – эллипс (причем, чем больше | h |,
тем меньше полуоси эллипса);
б) при | h | = c – точку C2,1(0; 0; c);
в) при | h | > c – мнимую кривую.
10.
zC2
A1
B1
x
A2
B2
y
C1
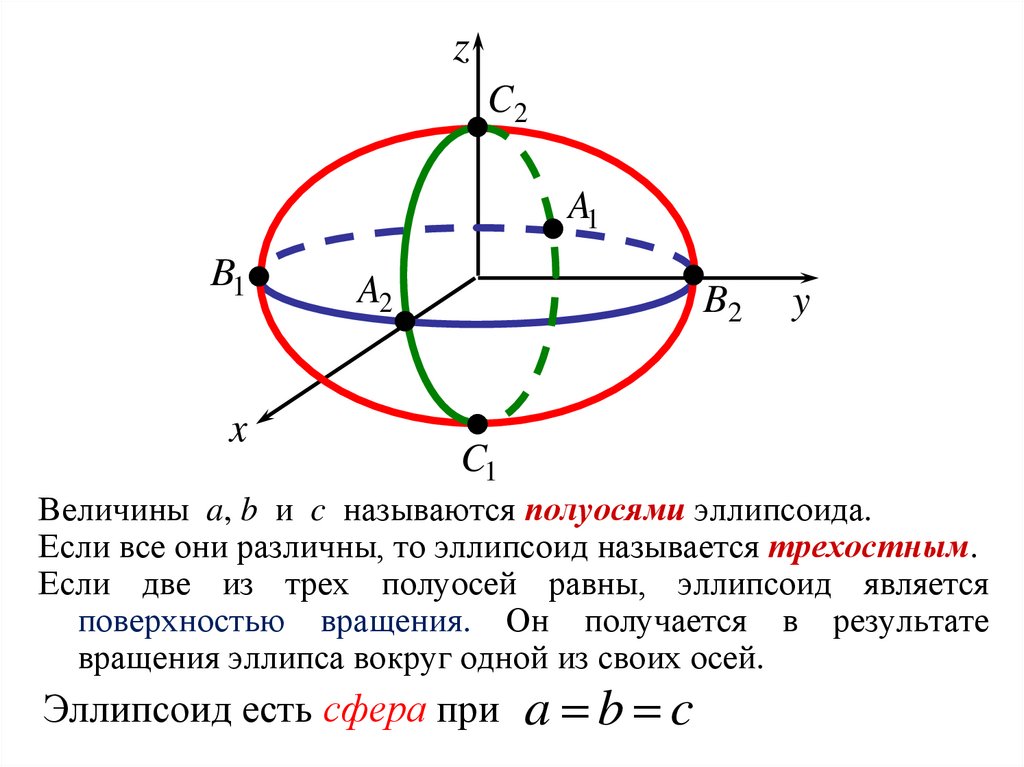
Величины a, b и c называются полуосями эллипсоида.
Если все они различны, то эллипсоид называется трехостным.
Если две из трех полуосей равны, эллипсоид является
поверхностью вращения. Он получается в результате
вращения эллипса вокруг одной из своих осей.
Эллипсоид есть сфера при a b c
11.
ОПРЕДЕЛЕНИЕ.Однополостным гиперболоидом называется поверхность
второго порядка, которая в некоторой прямоугольной
системе координат определяется уравнением
x2 y 2 z 2
2 2 1,
2
a
b
c
где a, b, c – положительные константы.
12. ИССЛЕДОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА
1) Сечения плоскостями x = h:x2 y 2 z 2
2 2 2 1,
a
b
c
x h .
y2 z2
h2
2 1 2 .
2
b
c
a
Это уравнение определяет
а) при | h | < a – гиперболу, с действительной осью || Oy;
б) при | h | > a – гиперболу, с действительной осью || Oz;
в) при | h | = a – пару прямых.
13.
3) Сечения плоскостями y = h:x2 y 2 z 2
2 2 2 1,
a
b
c
y h .
x2 z 2
h2
1
.
2
2
2
a
c
b
Это уравнение определяет
а) при | h | < b – гиперболу, с действительной осью || Ox;
б) при | h | > b – гиперболу, с действительной осью || Oz;
в) при | h | = b – пару прямых.
14.
3) Сечения плоскостями z = h:x2 y 2 z 2
2 2 2 1,
a
b
c
z h .
2
2
2
x
y
h
2 1 2 .
2
a
b
c
Это уравнение определяет эллипс при любом h.
При h = 0 полуоси эллипса будут наименьшими.
Этот эллипс называют горловым эллипсом
однополостного гиперболоида.
15.
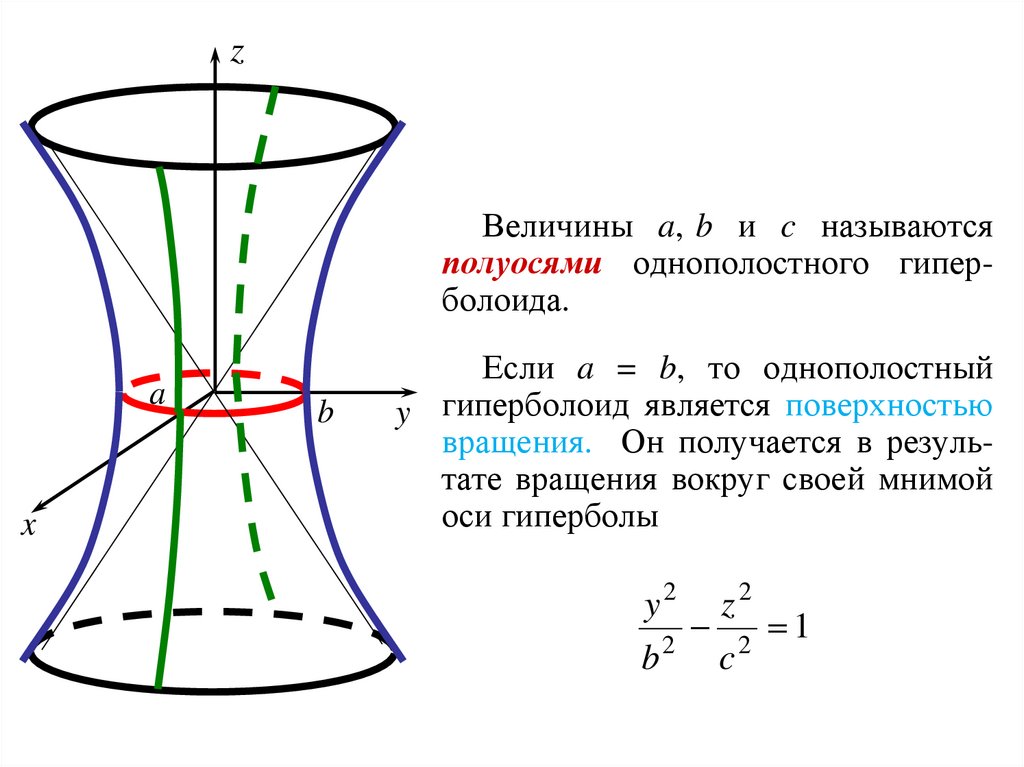
zВеличины a, b и c называются
полуосями однополостного гиперболоида.
a
x
b
Если a = b, то однополостный
y гиперболоид является поверхностью
вращения. Он получается в результате вращения вокруг своей мнимой
оси гиперболы
y2 z2
2 1
2
b
c
16.
Замечание.Уравнения
2
2
2
x
y
z
2 2 1,
2
a
b
c
2
2
2
x
y
z
2 2 2 1
a
b
c
определяют однополостные гиперболоиды, но они «вытянуты»
вдоль оси Oy и Ox соответственно.
Замечание
Однополостный гиперболоид имеет центр симметрии
O(0; 0; 0) и три плоскости симметрии xOy, xOz, yOz.
17.
Шуховская башнярасположена в Москве на улице Шаболовка, построена в 1919—
1922г. русским архитектором Владимиром Григорьевичем
Шуховым.
По форме секции башни — это
однополостные гиперболоиды
вращения, сделанные из прямых
балок, упирающихся концами в
кольцевые основания.
Такие конструкции часто
употребляются для устройства
высоких радиомачт, водонапорных
башен поскольку обеспечивают
минимальную ветровую нагрузку.
18.
ОПРЕДЕЛЕНИЕ.Двуполостным гиперболоидом называется поверхность
второго порядка, которая в некоторой прямоугольной
системе координат определяется уравнением
x2 y2 z 2
2 2 1 ,
2
a
b
c
где a, b, c – положительные константы.
19. ИССЛЕДОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ДВУПОЛОСТНОГО ГИПЕРБОЛОИДА
1)Сечения плоскостями x = h:
x2 y 2 z 2
2 2 2 1,
a
b
c
x h .
2
2
2
y
z
h
1
.
b2 c2
a2
При любом
h это уравнение определяет гиперболу, с
действительной осью || Oz.
20.
2) Сечения плоскостямиy = h:
x2 y 2 z 2
2 2 2 1,
a
b
c
y h .
2
2
2
x
z
h
2 1 2 .
2
a
c
b
При любом h это уравнение определяет гиперболу, с
действительной осью || Oz.
21.
3) Сечения плоскостями z = h:x2 y 2 z 2
2 2 2 1,
x2 y 2
h2
1
.
a
b
c
2
2
2
a
b
c
z h .
Это уравнение определяет
а) при | h | > c – эллипс (причем, чем больше | h |,
тем больше полуоси эллипса);
б) при | h | = c – точку C2,1(0; 0; c);
в) при | h | < c – мнимую кривую.
22.
zВеличины a, b и c называются
полуосями двуполостного гиперболоида.
c
y
x
Если a = b, то двуполостный гиперболоид является поверхностью
вращения. Он получается в результате вращения вокруг своей
действительной оси гиперболы
y2 z2
2 2 1
b
c
23.
Замечание.Уравнения
2
2
2
2
2
2
x y z
x y z
1
и
1
2
2
2
2
2
2
a b c
a b c
тоже определяют двуполостные гиперболоиды,
«вытянуты» вдоль оси Oy и Ox соответственно.
но
• Двуполостный гиперболоид имеет центр
симметрии O(0; 0; 0) и три плоскости
симметрии xOy, xOz, yOz.
они
24.
ОПРЕДЕЛЕНИЕ.Эллиптическим параболоидом называется поверхность
второго порядка, которая в некоторой прямоугольной
системе координат определяется уравнением
x2 y2
2 2z ,
2
a
b
где a, b – положительные константы.
25. ИССЛЕДОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ПАРАБОЛОИДА
1) Сечения плоскостями x = h:x2 y 2
2 2 2z ,
a
b
x h .
2
2
y
h
2
z
.
2
2
b
a
При любом h это уравнение определяет параболу. Ее ось || Oz,
ветви направлены вверх, параметр p = b2. При h 0 вершина
параболы смещена вверх.
26.
2) Сечения плоскостями y = h:x2 y 2
2 2 2z ,
a
b
y h .
2
2
x
h
2
z
.
2
2
a
b
При любом h это уравнение определяет параболу. Ее ось || Oz,
ветви направлены вверх, параметр p = a2. При h 0 вершина
параболы смещена вверх.
27.
3) Сечения плоскостямиx2 y 2
2 2 2z ,
a
b
z h .
z = h:
2
2
x
y
2
h
.
2
2
a
b
Это уравнение определяет
а) при h > 0 – эллипс (причем, чем больше h,
тем больше
полуоси эллипса);
б) при h = 0 – точку O (0; 0; 0);
в) при h < 0 – мнимую кривую.
28.
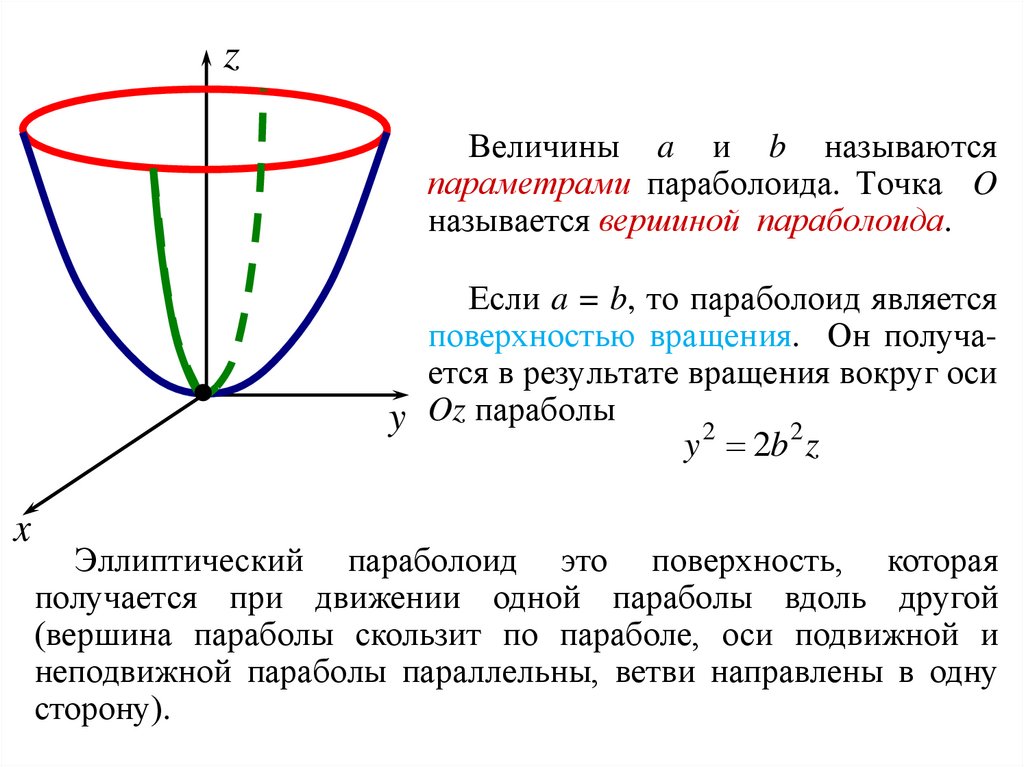
zВеличины a и b называются
параметрами параболоида. Точка O
называется вершиной параболоида.
Если a = b, то параболоид является
поверхностью вращения. Он получается в результате вращения вокруг оси
y Oz параболы
y 2 2b 2 z
x
Эллиптический параболоид это поверхность, которая
получается при движении одной параболы вдоль другой
(вершина параболы скользит по параболе, оси подвижной и
неподвижной параболы параллельны, ветви направлены в одну
сторону).
29.
Замечания:1) Уравнение
2
2
x
y
2
z
a 2 b2
тоже определяет эллиптический параболоид, но «развернутый» вниз.
2) Уравнения
x2 z 2
2 2 y ,
2
a
c
y2 z2
2 2 x
2
b
c
определяют эллиптические параболоиды, с осями симметрии
Oy и Ox соответственно.
Эллиптический параболоид имеет две плоскости симметрии
xOz, yOz.
30.
ОПРЕДЕЛЕНИЕ.Гиперболическим параболоидом называется поверхность
второго порядка, которая в некоторой прямоугольной
системе координат определяется уравнением
x2 y 2
2 2z ,
2
a
b
где a, b – положительные константы.
31. ИССЛЕДОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА
1)Сечения плоскостями x = h:
x
y
2 2 2z ,
a
b
x h .
2
2
2
2
y
h
2 2z 2 .
b
a
При любом h это уравнение определяет параболу. Ее ось || Oz,
ветви направлены вниз, параметр p = b2. При h 0 вершина
параболы смещена вверх.
32.
2) Сечения плоскостями y = h:x
y
2
2
2 2 2z ,
x
h
2
z
.
a
b
2
2
a
b
y h .
2
2
При любом h это уравнение определяет параболу. Ее ось || Oz,
ветви направлены вверх, параметр p = a2. При h 0 вершина
параболы смещена вниз.
33.
3) Сечения плоскостями z = h:x2 y 2
2 2 2z ,
a
b
z h .
2
2
x
y
2
h
.
2
2
a
b
Это уравнение определяет
а)
при h 0 – гиперболу
при h > 0 – действительная ось гиперболы || Ox,
при h < 0 – действительная ось гиперболы || Oy;
б) при h = 0 – пару прямых .
34.
zx
y
Величины a и b называются параметрами параболоида.
Гиперболический параболоид это поверхность, которая
получается при движении одной параболы вдоль другой
(вершина параболы скользит по параболе, оси подвижной и
неподвижной параболы параллельны, ветви направлены в
разные стороны).
35.
Замечания:1) Уравнение
x2 y 2
2 2 z
2
a
b
тоже определяет гиперболический параболоид, но «развернутый» вниз.
2) Уравнения
x2 z 2
y2 z2
2 2 y ,
2 2 x
2
2
a
c
b
c
определяют гиперболические параболоиды, у которых
«неподвижные параболы» лежат в плоскости xOy и имеют оси
Oy и Ox соответственно.
Гиперболический параболоид имеет две плоскости
симметрии xOz, yOz.
36. Цилиндры
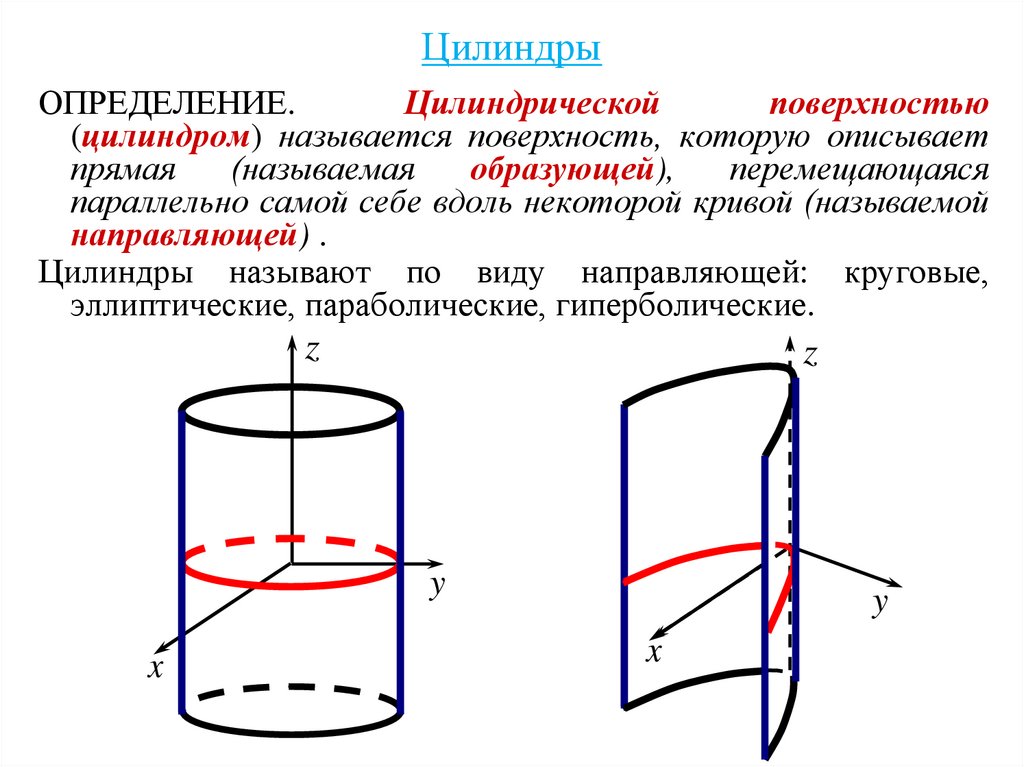
ОПРЕДЕЛЕНИЕ.Цилиндрической
поверхностью
(цилиндром) называется поверхность, которую описывает
прямая
(называемая
образующей),
перемещающаяся
параллельно самой себе вдоль некоторой кривой (называемой
направляющей) .
Цилиндры называют по виду направляющей: круговые,
эллиптические, параболические, гиперболические.
z
z
y
x
y
x
37. Классификация цилиндрических поверхностей второго порядка
Эллиптическийцилиндр
Параболический
цилиндр
38.
Гиперболический цилиндр39.
ЗамечаниеЦилиндр в некоторой декартовой системе координат
задается уравнением, в которое не входит одна из
координат.
Кривая,
которую
определяет
это
уравнение
в
соответствующей координатной плоскости, является
направляющей цилиндра; а образующая – параллельна оси
отсутствующей координаты.
40. Конические поверхности 2-го порядка
Определение Коническая поверхность-поверхность, образованная прямыми
(образующими конуса), проходящими через
данную точку (вершину конуса) и пересекающими
данную линию (направляющую конуса).
2
2
2
x
y
z
2 2 0
2
a
b
c
41. ИССЛЕДОВАНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ КОНУСА
1)Сечения плоскостями x = h:
x2 y 2 z 2
2 2 2 0,
a
b
c
x h .
2
2
2
y
z
h
.
2
2
2
b
c
a
Это уравнение определяет
а) при h 0 – гиперболу, с действительной осью || Oz;
б) при h = 0 – пару прямых.
42.
2) Сечения плоскостями y = h:x2 y 2 z 2
2 2 2 0,
a
b
c
y h .
2
2
x
z
h
.
2
2
2
a
c
b
Это уравнение определяет
а) при h 0 – гиперболу, с действительной осью || Oz;
б) при h = 0 – пару прямых.
2
43.
3). Сечения плоскостямиz = h:
x2 y 2 z 2
2 2 2 0,
a
b
c
z h .
2
2
x
y
h
2 2.
2
a
b
c
Это уравнение определяет
а) при h 0 – эллипс (причем, чем больше | h |,
тем больше полуоси эллипса);
б) при h = 0 – точку O (0; 0; 0).
2
44.
zВеличины a, b и c называются
полуосями конуса.
Центр симметрии O называется
вершиной конуса.
y
x
Если a = b, то конус является поверхностью вращения. Он получается в результате вращения вокруг
оси Oz прямой
c
z y
b
45.
Замечание.Уравнения
2
2
2
2
2
2
x
y
z
x
y
z
0
и
0
2
2
2
2
2
2
a
b
c
a
b
c
тоже определяют конусы, но они «вытянуты» вдоль оси Oy и
Ox соответственно.









































 Математика
Математика








