Похожие презентации:
Сети Петри
1. Сети Петри
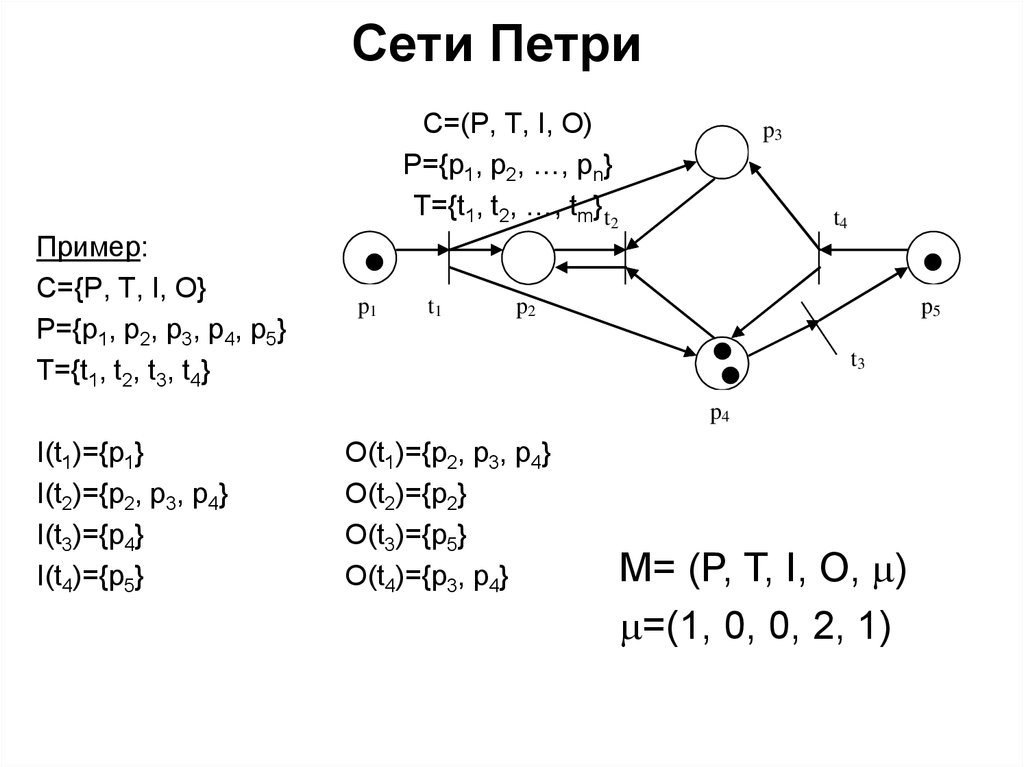
Пример:C={P, T, I, O}
P={p1, p2, p3, p4, p5}
T={t1, t2, t3, t4}
С=(P, T, I, O)
P={p1, p2, …, pn}
T={t1, t2, …, tm} t2
p1
t1
p3
t4
p2
p5
t3
p4
I(t1)={p1}
I(t2)={p2, p3, p4}
I(t3)={p4}
I(t4)={p5}
O(t1)={p2, p3, p4}
O(t2)={p2}
O(t3)={p5}
O(t4)={p3, p4}
M= (P, T, I, O, )
=(1, 0, 0, 2, 1)
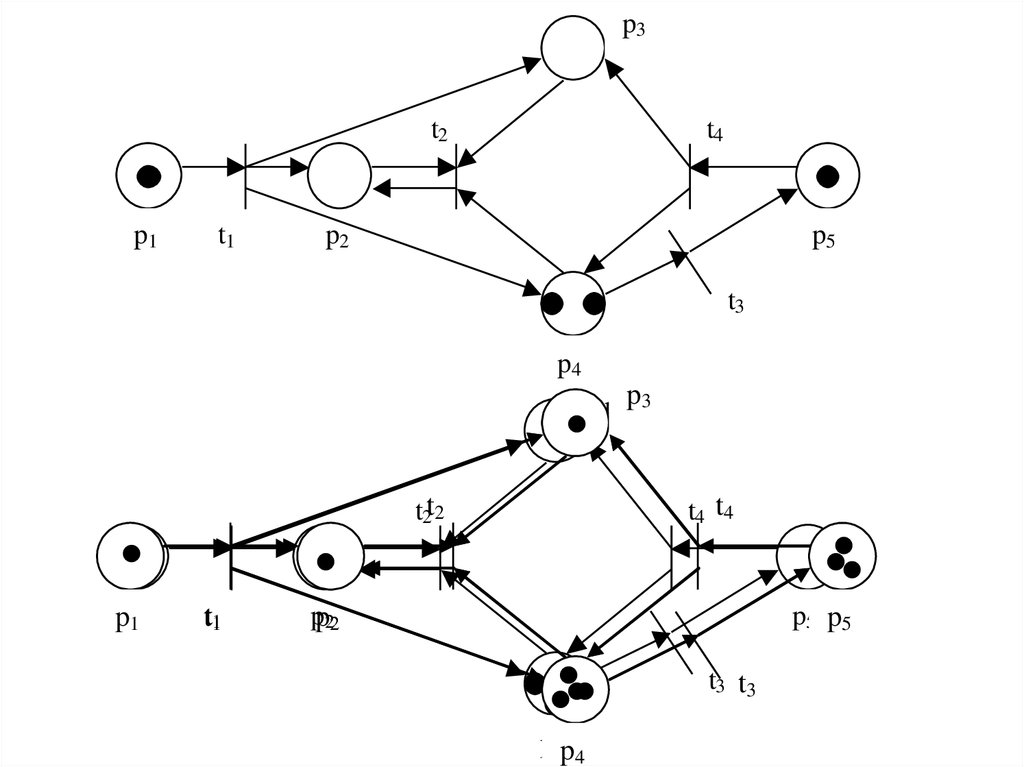
2.
p3t2
p1
t1
t4
p2
p5
t3
p4
p3p3
t2t2
pp11
t1
t4 t4
pp22
p5 p5
t3 t3
p4p4
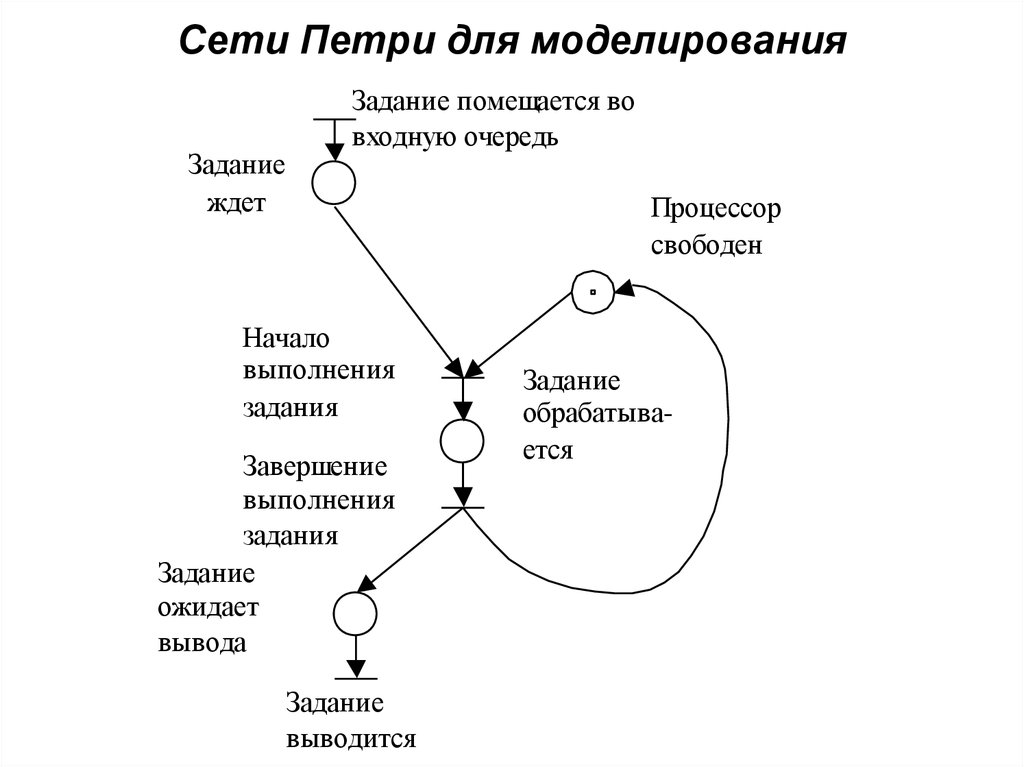
3. Сети Петри для моделирования
Заданиеждет
Задание помещается во
входную очередь
Начало
выполнения
задания
Завершение
выполнения
задания
Задание
ожидает
вывода
Задание
выводится
Процессор
свободен
Задание
обрабатывается
4.
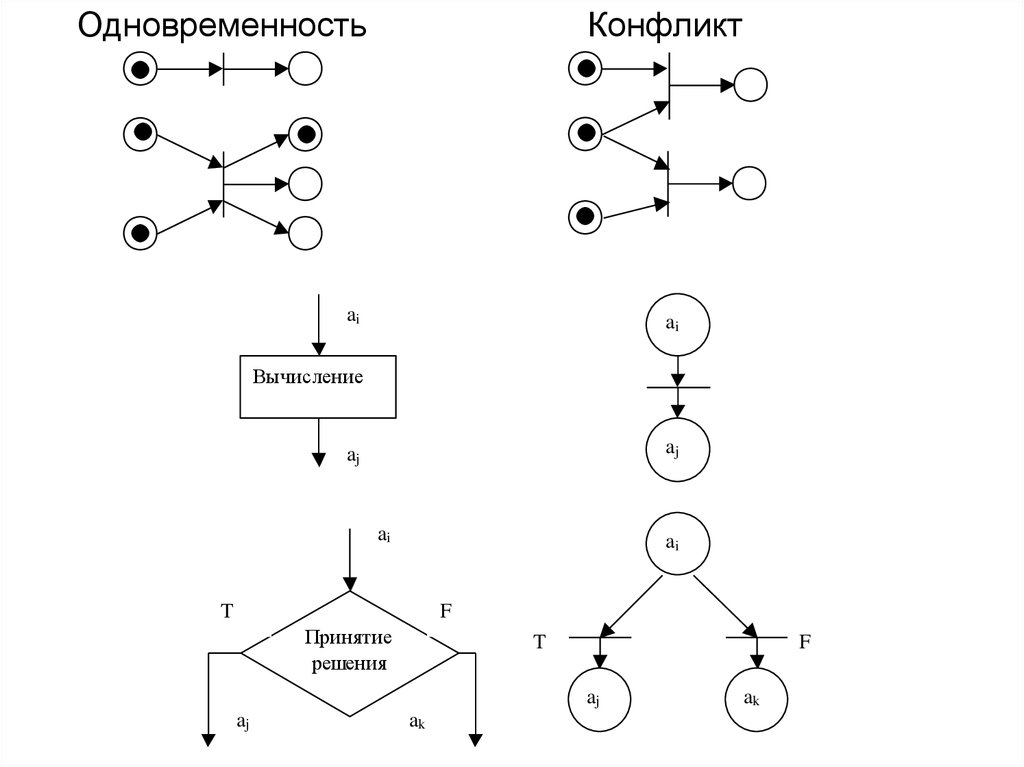
ОдновременностьКонфликт
ai
ai
Вычисление
aj
aj
ai
ai
T
F
Принятие
решения
T
F
aj
aj
ak
ak
5.
6.
Е3Е4
С3
М3
М4
С4
С2
М2
М5
Е2
С5
С1
М1
Е1
Е5
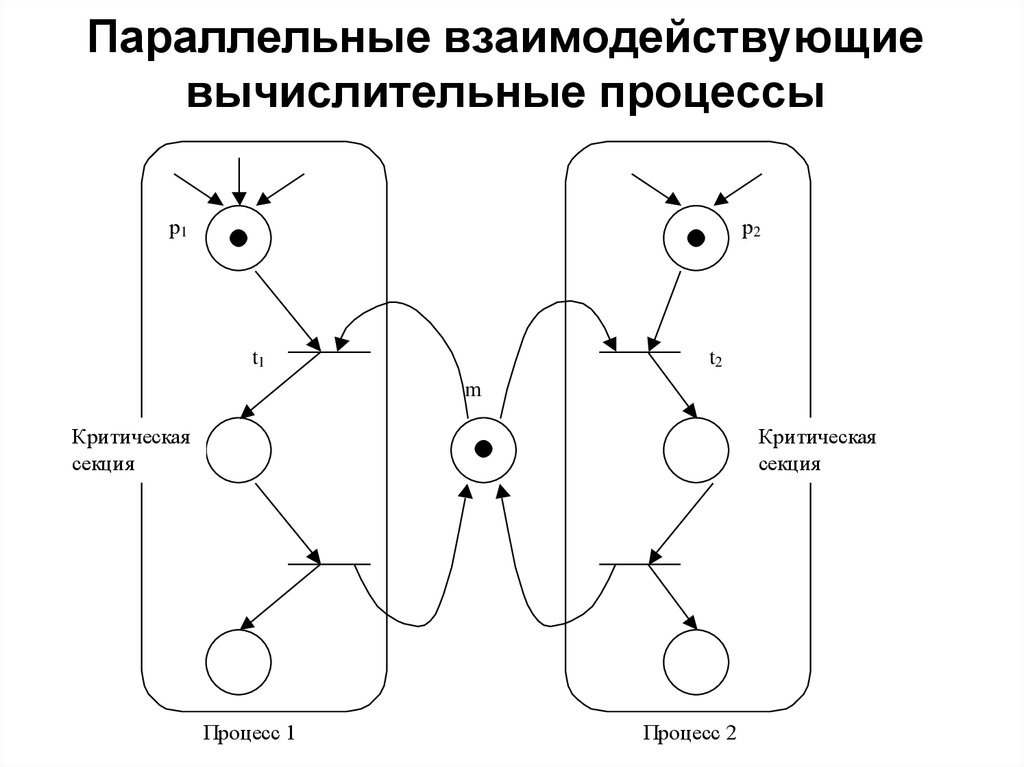
7. Параллельные взаимодействующие вычислительные процессы
р1р2
t1
t2
m
Критическая
секция
Критическая
секция
Процесс 1
Процесс 2
8. Средства синхронизации и связи
• Блокировка памяти• Операция «Проверка и установка»
9. Семафоры Дейкстры
P(S)V(S)
P(S): S:=S-1;
if S<0, then {остановить процесс и поместить его в
очередь ожидания к семафору S}
V(s): if S<0 then {поместить один из ожидающих процессов
очереди семафора S в очередь готовности};
S:=S+1
InitSem (имя_семафора, начальное_значение_семафора);
10.
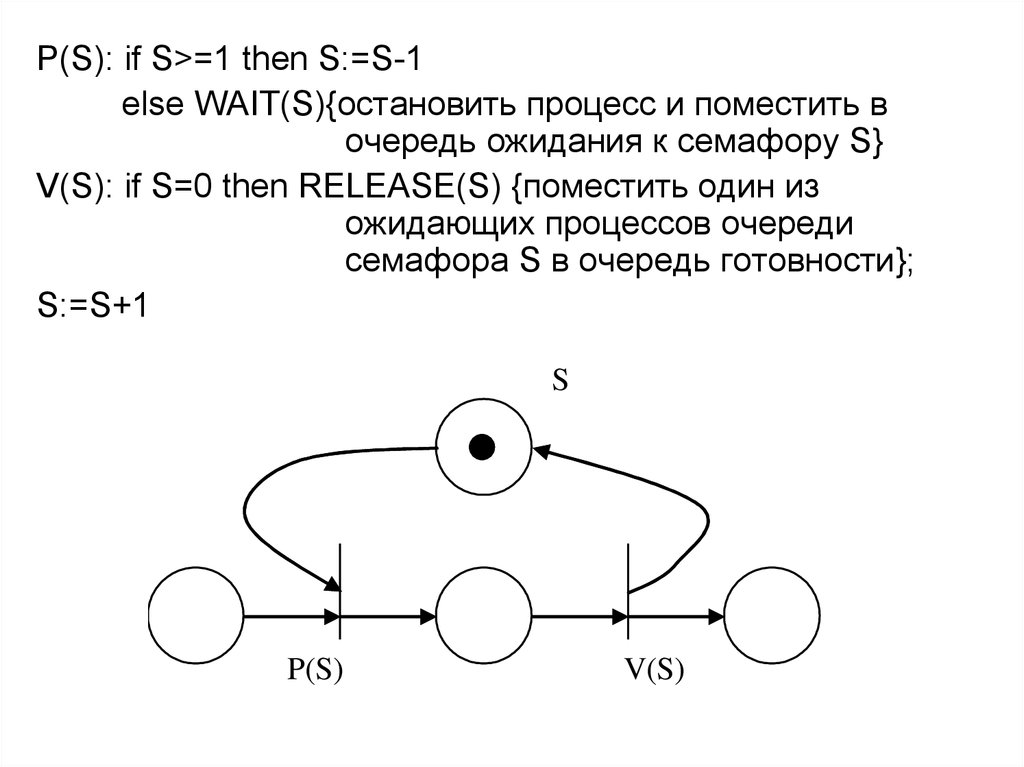
P(S): if S>=1 then S:=S-1else WAIT(S){остановить процесс и поместить в
очередь ожидания к семафору S}
V(S): if S=0 then RELEASE(S) {поместить один из
ожидающих процессов очереди
семафора S в очередь готовности};
S:=S+1
S
P(S)
V(S)
11.
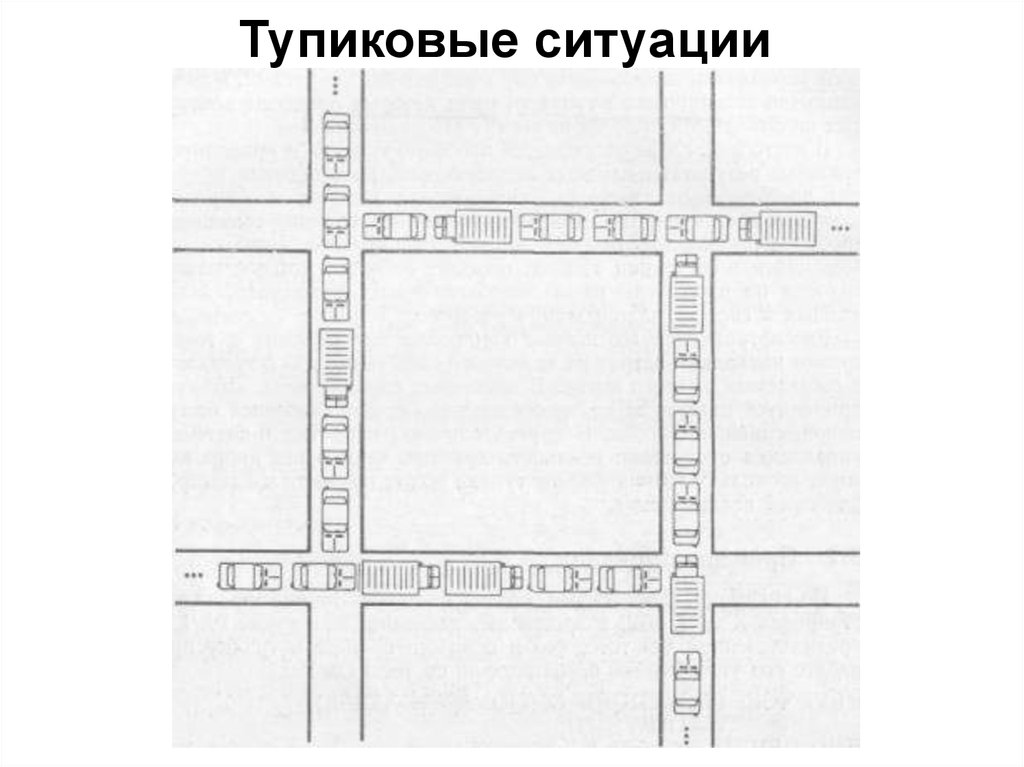
Тупиковые ситуации12.
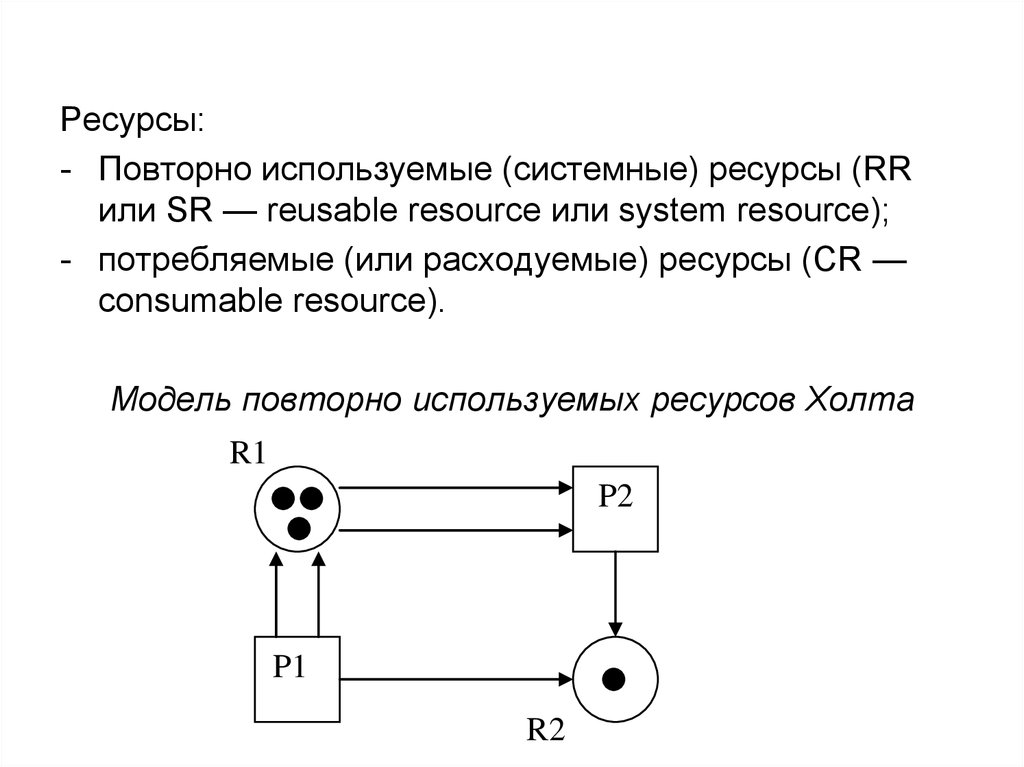
Ресурсы:- Повторно используемые (системные) ресурсы (RR
или SR — reusable resource или system resource);
- потребляемые (или расходуемые) ресурсы (CR —
consumable resource).
Модель повторно используемых ресурсов Холта
R1
P2
P1
R2
13.
Условия возникновения тупика:• взаимного исключения;
• ожидания;
• отсутствия перераспределения;
• кругового ожидания.
14. Формальные модели для изучения проблемы тупиковых ситуаций
•Сети Петри•Вычислительные схемы
•Модель пространства состояний
•Модель Холта
15. Сети Петри
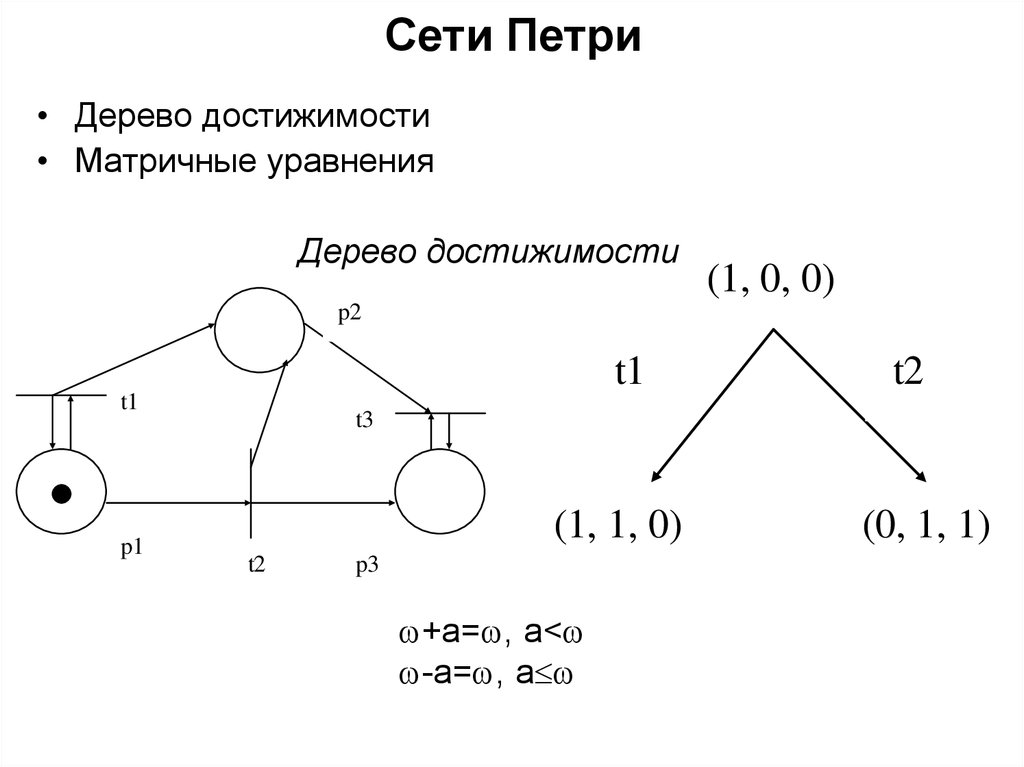
• Дерево достижимости• Матричные уравнения
Дерево достижимости
(1, 0, 0)
p2
t1
t1
p1
t2
t3
(1, 1, 0)
t2
p3
+a= , a<
-a= , a
(0, 1, 1)
16.
Классификация вершин:граничная;
терминальная;
дублирующая;
внутренняя.
Алгоритм:
[x]= [y], х – дублирующая;
[x], х – терминальная;
tj T, [x], z. [z], pi:
- [x]i=ω, [z]i=ω;
- [у]< ( [x], tj) и [у]i< ( [x], tj)i , то [z]i= ;
- [z]i= ( [x], tj)i .
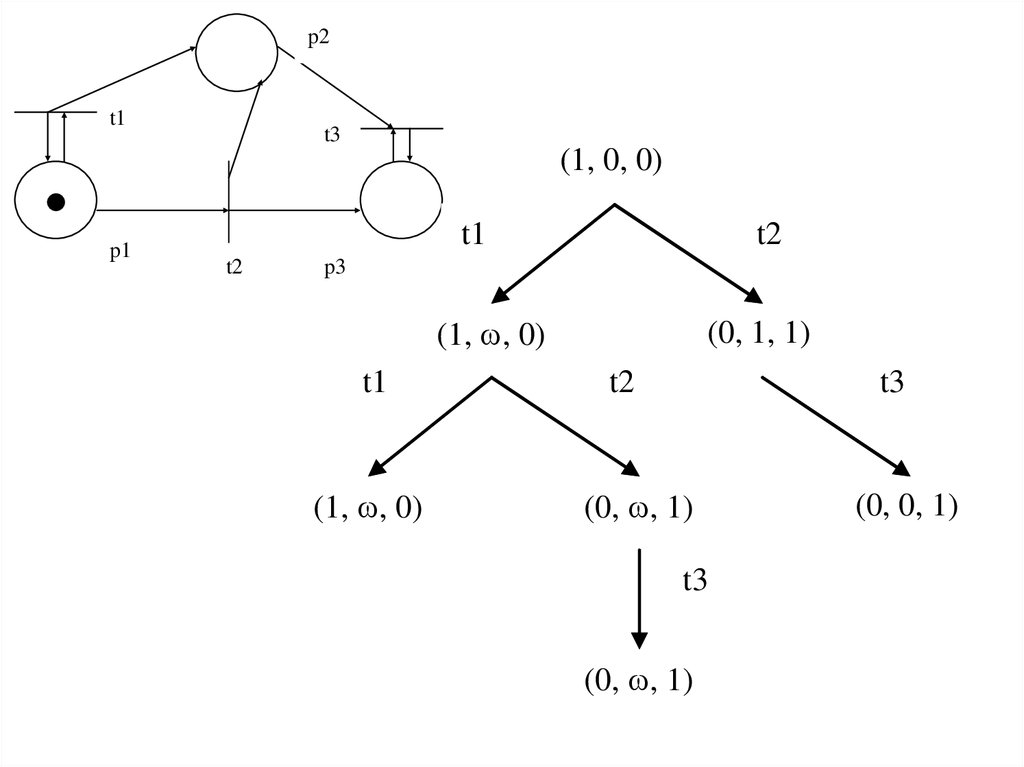
17.
p2t1
t3
(1, 0, 0)
p1
t1
t2
t2
p3
(1, , 0)
t1
(1, , 0)
(0, 1, 1)
t2
t3
(0, , 1)
t3
(0, , 1)
(0, 0, 1)
18. Матричные уравнения
DD+D=D+-D• D-[i, j]=#(pi, I(tj))
• D+[j, i]=#(pi, O(tj))
p1
p2
t1
p4
p3
1 1 1 0
D 0 0 0 1
0 0 1 0
t2
1 0 0 0
D 0 2 1 0
0 0 0 1
t3
0 1 1 0
D 0 2 1 1
0 0 1 1
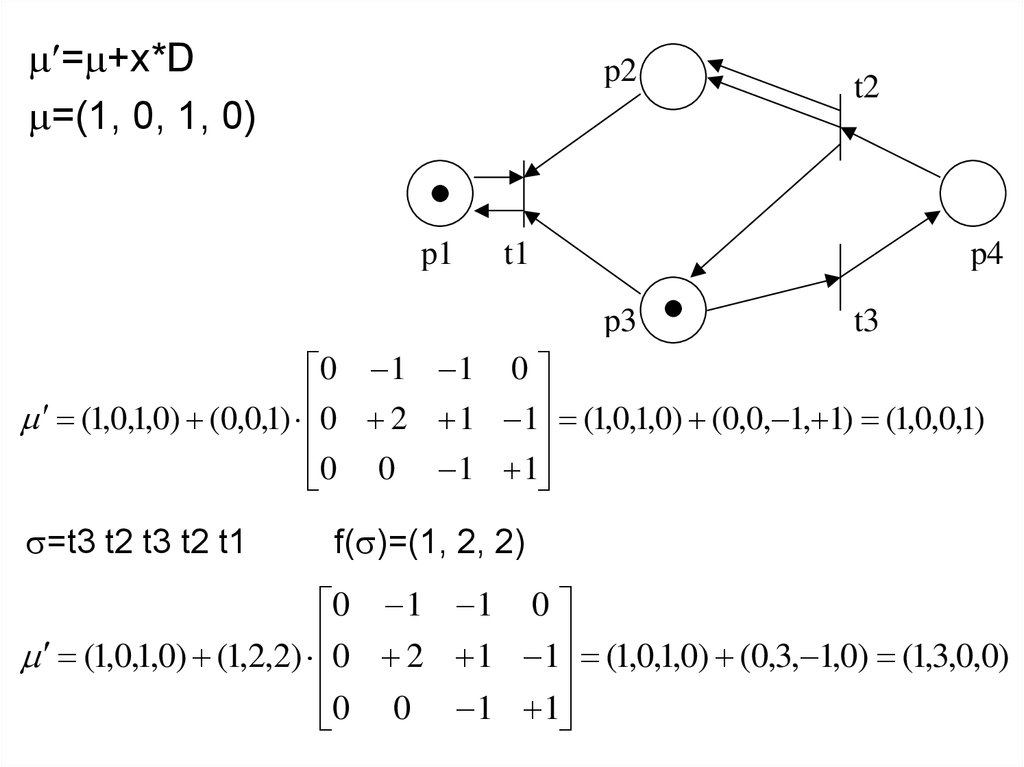
19.
= +х*D=(1, 0, 1, 0)
p2
p1
t2
t1
p4
p3
t3
0 1 1 0
(1,0,1,0) (0,0,1) 0 2 1 1 (1,0,1,0) (0,0, 1, 1) (1,0,0,1)
0 0 1 1
=t3 t2 t3 t2 t1
f( )=(1, 2, 2)
0 1 1 0
(1,0,1,0) (1,2,2) 0 2 1 1 (1,0,1,0) (0,3, 1,0) (1,3,0,0)
0 0 1 1
20.
=(1, 0, 1, 0)’=(1, 8, 0, 1)
0 1 1 0
(1,8,0,1) (1,0,1,0) x 0 2 1 1 ,
0 0 1 1
х=(0, 4, 5)
=t3 t2 t3 t2 t3 t2 t3 t2 t3









 Математика
Математика Информатика
Информатика








