Похожие презентации:
Шахматы - одна из самых древних игр
1.
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕПОЧИНКОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
с. ПОЧИНКИ НИЖЕГОРОДСКОЙ ОБЛАСТИ
(Алгебра – 9)
Автор: учитель математики
Напалкова Елена Серафимовна
2.
Шахматы – одна из самых древнихигр. Она существует уже многие века
и неудивительно, что с нею связаны
различные предания, правдивость
которых, за давностью времени,
невозможно проверить.
Шахматная игра была придумана
в Индии, и когда индусский царь
Шерам познакомился с нею, он был
восхищен ее остроумием и
разнообразием возможных в ней
положений.
3.
Узнав, что она изобретенаодним из его подданных, царь
приказал его позвать, чтобы
лично наградить за удачную
выдумку.
Изобретатель, его звали
Сета, явился к трону повелителя.
- Я желаю достойно
вознаградить тебя .
Мудрец молчал.
- Я достаточно богат, чтобы
исполнить твоё самое смелое
пожелание. Назови награду ,
которая тебя удовлетворит.
4.
- Повелитель,- сказал Сета,прикажи выдать мне за первуюклетку шахматной доски одно
пшеничноё зерно, за вторую – 2, за
третью - 4, за четвёртую – 8, за
пятую – 16…
- Довольно, - с раздражением
прервал его царь. – Ты получишь
свои зёрна за всё 64 клетки доски.
Но знай, что просьба твоя
недостойна моей щедрости.
Сета улыбнулся и покинул залу.
5.
Отходя ко сну царь вспомнил обизобретателе шахмат и спросил:
-Унёс ли Сета свою жалкую награду?
- Повелитель ,- ответили ему, математики
твои трудятся без отдыха и надеются к
рассвету закончит подсчёт.
Утром царю доложили , что число это так
велико, что в его амбарах нет такого
количества зёрен.
6. Что за последовательность чисел получилась?
1 ; 2 ; 4 ; 16 ; 32 ; 64….В этой последовательности каждый её
член, начиная со второго, равен
предыдущему, умноженному на два.
Такая последовательность называется
геометрической прогрессией.
7. Определение геометрической прогрессии.
Числовая последовательностьb1 ; b2 ; b3 ;….; bn;…
называется геометрической прогрессией,
если для всех натуральных n выполняется
равенство bn+1 = bnq ,
где bn ≠ 0, q – некоторое число , не равное
нулю.
q называется знаменателем прогрессии.
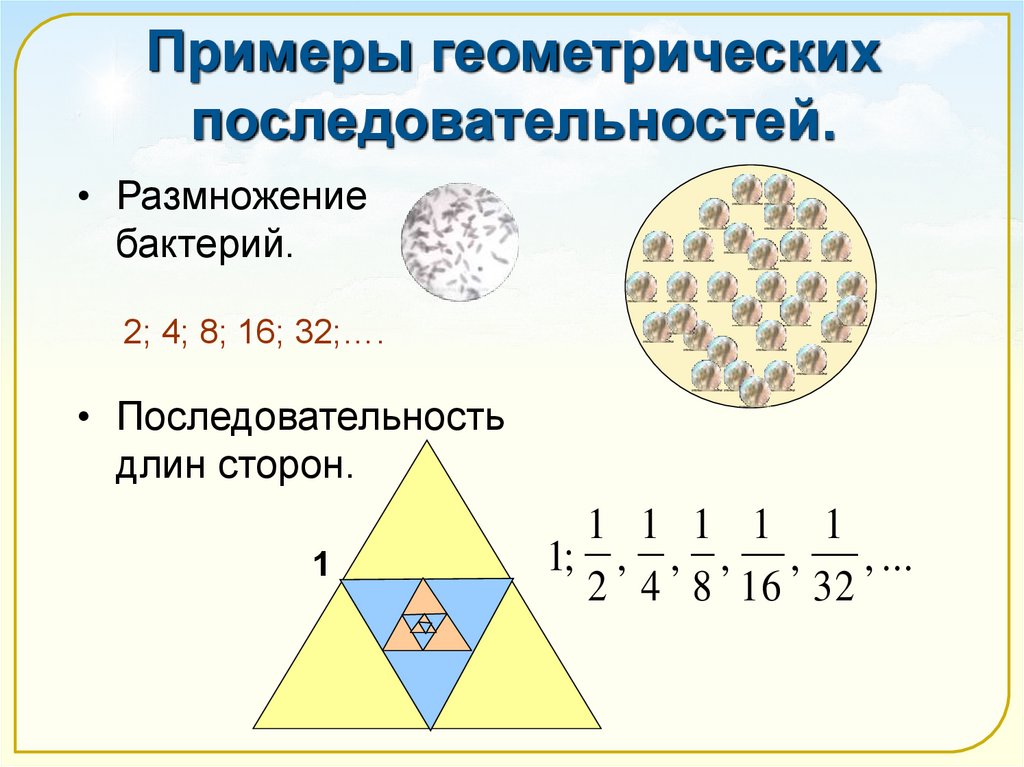
8. Примеры геометрических последовательностей.
• Размножениебактерий.
2; 4; 8; 16; 32;….
• Последовательность
длин сторон.
1
1 1 1 1 1
1; , , , , , ...
2 4 8 16 32
9. Свойство геометрической прогрессии.
bn+1 = bnqbn-1 = bn : q
Перемножим эти равенства
bn+1∙ bn-1 = (bnq) ∙ (bn : q) = bn2
bn bn 1 bn 1
10.
• Если все члены прогрессии положительны, тоbn bn 1 bn 1 ,
т. е. каждый член, начиная со второго, равен
среднему геометрическому двух соседних с
ним членов.
• Этим объясняется название
«геометрическая» прогрессия.
11. Формула n – го члена геометрической прогрессии.
bn+1 = bnqb2 = b1q
b3 = b2q = b1q2
b4 = b3q = b1q3
………………………
bn = b1qn-1
12. Задача №1.
Найти седьмой член геометрической1
прогрессии, если b1 = 81, q =
.
Решение.
b n = b1q
3
n -1
1
b7 81
3
7 1
4
1
81 3
6 = 6 .
9
3
3
13. Задача № 2.
Дано : b1 2, b2 6, bn 486.Найти : n.
Решение.
bn=b1·qn-1
b2 6
1) q
3,
b1 2
2) bn=2·3n-1= 486,
n 1 5,
3n-1= 243,
n 6.
3n-1= 35,
Ответ : 6.
14. Задача № 3 .
На луг площадью 12800 м2 попали семенаодуванчика и со временем заняли 50м2. При
благоприятных условиях одуванчик
размножаясь, занимает площадь вдвое
большую, чем в прошлом году. Через сколько
лет одуванчики займут весь луг?
15.
Решение.Дано:
b1=50,
bn=12800,
q=2.
Найти: n.
bn=b1·qn-1
bn=50·2n-1= 12800,
2n-1= 256,
2n-1= 28,
n – 1 = 8,
n = 9.
Ответ: через 9 лет.
16. Закрепление.
• Какая последовательность называетсягеометрической прогрессией?
• Почему она так называется?
• Как вычислить n – й член геометрической
прогрессии?
















 Спорт
Спорт








