Введение в теорию вероятности

1.

Математика
5 класс

2.

Александр Сергеевич Пушкин
О, сколько нам открытий чудных
Готовят просвещенья дух
И опыт, сын ошибок трудных,
И гений, парадоксов друг,
И случай, бог изобретатель.
Михаил Юрьевич Лермонтов
Я к вам пишу случайно; право,
Не знаю как и для чего.
Я потерял уж это право.
И что скажу вам? — ничего!
Алексей Константинович Толстой
Средь шумного бала, случайно,
В тревоге мирской суеты,
Тебя я увидел, но тайна
Твои покрывала черты.
Александр Александрович Блок
Жизнь - без начала и конца.
Нас всех подстерегает случай.
Над нами - сумрак неминучий,
Иль ясность божьего лица.

3. Блез Паскаль Пьер Ферма

4.

А что получилось у тебя?

5.

Два ученика провели эксперимент c подбрасыванием монеты и
результаты оформляли в виде таблицы размером 10 клеток на 10,
раскрашивая при этом клеточку в зеленый цвет, если при бросании
монеты выпадет герб, а если решка - в красный.
Получились мозаики из красных и зеленых скоплений. Вот такие.
Такую мозаику формирует случай.

6.

Знаменитый французский
естествоиспытатель Бюффон
(1707 – 1788) проделал этот опыт 4040 раз,
при этом выпадение «орла» равнялось
2048.
Английский математик Пирсон (1857 – 1936)
повторил опыт 12000 раз, число выпадений
герба составило 6019.

7. Гнеденко Борис Владимирович

Колмогоров
Андрей Николаевич

8.

Ляпунов
Чебышёв
Александр
Пафнутий
Михайлович Львович
Буняковский
Виктор
Яковлевич

9.

Бросание кубика можно считать опытом,
экспериментом, испытанием ( или даже игрой,
забавой), а полученный результат – СОБЫТИЕМ.

10.

КЛАССИФИКАЦИЯ СОБЫТИЙ
• Событие, которое обязательно произойдет в
данном опыте, называют Достоверным
событием.
Например, событие: выпадет цифра от 1 до 6, является
достоверным.
• Событие, которое не может произойти в этом
опыте, называется Невозможным событием.
В нашем примере таковым является событие: выпадет цифра 7
• Событие, если оно может произойти, а может и не
произойти в данном опыте, называется
Случайным событием.
Событие: выпадет цифра 1 может наступить, а может и не
наступить.

11. Охарактеризуйте события, о которых пойдет речь, как достоверные, случайные и невозможные.

Меня завтра спросят на уроке
Летом у меня будут каникулы
Мне сегодня встретится черная кошка
День рождения моего друга – число меньшее 32.
Из школьного окна видно море
Завтра будет воскресенье, если сегодня суббота.
Выбрали наугад слово из книги, и в нем есть буква о.
Камень, брошенный в воду, утонет.
Когда ты станешь взрослым, тебя изберут
Президентом России.

12. В ящике имеются 4 белых и 7 черных шаров. Из ящика наугад выбирают шар.

•Вынутый шар белого цвета
•Вынутый шар черного
•Случайное
цвета
•Вынутый шар зеленого
•Достоверное
цвета
•Вынутый шар черного или
белого цвета
•Невозможное

13. В корзине лежало 3 красных и 3 жёлтых яблока. Из сумки наугад вынимают яблоко. Среди следующих событий укажите случайные,

достоверные, невозможные события.
А: Вынуто красное яблоко
СЛУЧАЙНЫЕ
В: Вынуто жёлтое яблоко
С: Вынуто зелёное яблоко
D:
Вынуто яблоко
НЕВОЗМОЖНОЕ
ДОСТОВЕРНОЕ

14.

Три господина, придя в ресторан , сдали в гардероб свои шляпы.
Расходились они по домам последними, и притом в полной
темноте, поэтому разобрали свои шляпы наугад . Какие из
следующих событий случайные, невозможные, достоверные?
А: «каждый надел свою шляпу».
В: «все надели чужие шляпы».
С: « двое надели чужие шляпы , а один - свою».
D: « двое надели свои шляпы , а один - чужую».
ОТВЕТ: события
А,В,С – случайные,
событие D - невозможное

15. Задача

• В коробке лежат 6 красных, 2 синих и 1 зелёный
карандаш.
Один из карандашей выпал и закатился под стол.
Даша закричала первая: «Если он зелёный, то я
беру его себе!» Данила сказал: «Если карандаш
синий, то я беру его себе.» Андрей, подумав,
предложил: «Если карандаш не зелёный и не
синий, то я беру его себе».
Как вы думаете, у кого из детей больше шансов
получить выпавший карандаш?

16.

В теории вероятностей чаще, чем в большинстве других
областей математики, встречаются результаты,
противоречащие интуиции, а против решения иных задач
восстает здравый смысл.
В мешке 3 желтых шара и 1 синий. Как вы думаете, что
вероятнее вытащить:
2 желтых или 1 желтый и 1 синий?
Наверное, многие сразу скажут: два желтых, ведь их больше!
И будут неправы! Чтобы это понять, обозначим шары.
У нас три желтых:
и один синий Мы можем вытащить два шара так:
То есть три способа вытащить два желтых и три способа вытащить
желтый и синий. А значит вероятности равны!
Такие события называются равновероятными или равновозможными.
Именно на этом парадоксе основаны некоторые карточные фокусы. Во многих
азартных играх нельзя полагаться на интуицию, ибо последствия могут быть
самыми неприятными.

17. Через мгновение Вы войдете в мир магии...

18.

…Вы столкнетесь с
необъяснимым.

19. Вы станете частью иллюзии...

20. …иллюзии Копперфильда.

21. Вы увидите,

22. Что я могу узнать, что Вы думаете.

23.

Вы видите 6 карт.
Выберите одну карту.
Просто думайте о ней.
ДУМАЙТЕ.

24.

Смотрите в мои глаза.
Просто думайте о
загаданной карте.

25.

Я Вас не знаю.
Я не могу видеть Вас..
Но я знаю, что Вы
думаете.

26.

СМОТРИТЕ,
Я забрал
Вашу карту !!!

27.

Я знал тот выбор,
который Вы сделаете!

28.

Слово "комбинаторика" происходит от латинского "combinare", которое
означает "соединять, сочетать".
Комбинаторика - раздел математики, в котором изучаются вопросы о
том, сколько различных комбинаций, подчиненных тем или иным
условиям, можно составить из заданных объектов.
С похожими задачами люди столкнулись в глубокой древности.
Комбинаторные задачи возникали и в связи с такими играми, как шашки,
шахматы, домино, карты, кости и др.
Комбинаторика становится наукой в XVII в., когда возникла теория
вероятностей. Чтобы решать теоретико-вероятностные задачи, нужно было
уметь подсчитывать число различных комбинаций, подчиненных тем или
иным условиям. Комбинаторными задачами интересовались и математики,
занимавшиеся составлением и разгадыванием шифров, изучением древних
рукописей. После создания компьютеров, с помощью которых стало
возможным делать вычисления, требовавшие ранее сотен и тысяч лет,
применение комбинаторики расширилось. Сейчас комбинаторика находит
приложения во многих областях науки: в биологии, в химии, механике и т.д.

29.

Наверное, ты знаешь фильм "Кин-дза-дза".
Жители планеты Кин-дза-дза обходились для
всех случаев одним словом "ку".
А если бы алфавит у них состоял из двух букв
К и У, то сколько слов было бы у них в
словаре, при условии, что буквы в слове
могут повторяться, и слова состоят только
из двух букв?
Решение:
Можно составить слова: "Ку ", " Кк ", " Уу " и "Ук".
Если эта задачка показалась тебе слишком лёгкой,
то следующая задача потруднее.

30. Задача 1

Туристическая фирма
планирует посещение
туристами в Италии
трех городов: Венеции,
Рима и Флоренции.
Сколько существует
вариантов такого
маршрута?
30

31. Решение

*
В
Ф
Р
Р
Ф
Ф
В
Р
В
Ф
Р
В
Ф
В
Р
ВРФ ВФР РФВ РВФ ФРВ ФВР

32.

• В этой задаче нам пришлось
перебрать все возможные
варианты, или , как обычно
говорят в таких случаях – все
возможные комбинации.
Поэтому подобные задачи
называют комбинаторными.

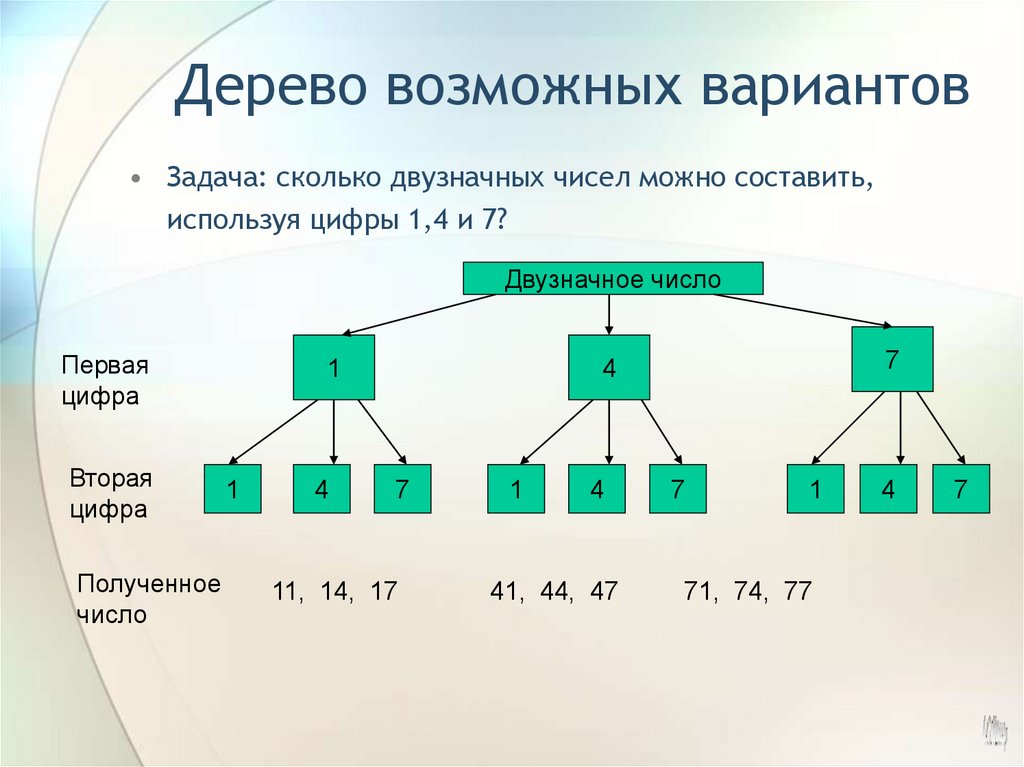
33. Дерево возможных вариантов

• Задача: сколько двузначных чисел можно составить,
используя цифры 1,4 и 7?
Двузначное число
Первая
цифра
Вторая
цифра
Полученное
число
1
1
4
7
4
7
11, 14, 17
1
4
41, 44, 47
7
1
71, 74, 77
4
7

34.

Сколько двузначных чисел можно
составить из цифр 9 , 7 и 0 ?
Попробуйте самостоятельно построить
дерево возможных вариантов.
Полученные числа: 99, 97, 90, 79, 77, 70

35.

• Задача
Несколько стран решили использовать для
своего государственного флага символику в виде
трех горизонтальных полос одинаковой ширины
разных цветов: красного, белого, зеленого.
Сколько стран могут использовать такую
символику?

36.

Решение:
Построим дерево различных вариантов.
1 полоса
2 полоса
3 полоса
з
б к
к б
Итого получилось 6 вариантов.
б
к
з
к
з
к
б з
з б

37.

Васе очень надо позвонить приятелю, но он
забыл две последних цифры шестизначного
телефонного номера. (Согласитесь, такое может
случиться с каждым.) Он пытается угадать их, не
получается. Тогда он решает перепробовать
комбинации всех забытых цифр .
Какое наибольшее число звонков предстоит
сделать Васе, чтобы в результате дозвониться
до приятеля?
Давайте разберемся.
Васе предстоит проверить 10 вариантов выбора последней
цифры (всего 10 цифр: 0, 1, 2,...8, 9). Для каждой из этих цифр
надо проверить 10 вариантов выбора предпоследней цифры.
Например, если последняя цифра 1, то предпоследняя может
быть: 0, 1, ...7, 8, 9. Остальные цифры ему известны, их не надо
угадывать. Так что получается, что наибольшее число вариантов
номеров, которые предстоит проверить Васе, равно 10·10=100
Наверное, если бы он подумал, то не стал бы и начинать.

38. Итак,

• Событие, которое в данном опыте
обязательно наступит, называется…
• Событие, которое в данном опыте
наступить не может, называется…
• Событие, которое в данном опыте
может как наступить, так и не
наступить, называется…

39.

1.Укажите, какие из перечисленных событий, по вашему
мнению, являются достоверными, а какие —
невозможными:
А = на игральном кубике кости выпало 0 очков;
В = на игральном кубике выпало от одного до шести очков;
С = номер открытой страницы в книге — дробное число;
E = номер открытой страницы в книге не меньше 1;
F = 1 января в школе не будет уроков.
2. Являются ли достоверными события:
A = на игральной кости выпало четное число очков;
B = на игральной кости выпало целое число очков?
C = завтра на улице вам встретится Баба-Яга;
D = число дней в следующем месяце не превысит 31;
E = в вашей ванне поселится красный крокодил в синюю
полоску;
F = на морозе вода в стакане через некоторое время
замерзнет;
G = сборная нашего класса выиграет в футбол у "Спартака".

40.

41. Случай в твоей жизни

1. В жизни каждого, наверно, бывают разные непредсказуемые
случаи, которые меняют размеренное течение жизни и
запоминаются надолго. Попробуй вспомнить какое-то
неожиданное событие. Случай может быть забавным и не очень.
Ты можешь составить устно небольшой рассказик, а можешь
нарисовать. Главное, чтобы это было случайное событие,
которое произошло с тобой.

42.

2. Бросаем два кубика. Какие из следующих событий
невозможные, какие – случайные, а какие – достоверные:
А = на кубиках выпало одинаковое число очков;
B = сумма очков на кубиках не превосходит 12;
С = сумма очков на кубиках равна 11;
D = произведение очков на кубиках равно 11.
3. В классе учится 10 мальчиков и 20 девочек. Какие из
следующих событий являются для такого класса
невозможными, какие – случайные, а какие – достоверные:
А = в классе есть два человека, родившихся в разные месяцы;
B = в классе есть два человека, родившихся в одном месяце;
С = в классе есть два мальчика, родившихся в одном месяце;
D = в классе есть две девочки, родившиеся в одном месяце;
Е = все мальчики родились в разные месяцы;
F = все девочки родились в разные месяцы;
G = есть мальчик и девочка, родившиеся в одном месяце;
H = есть мальчик и девочка, родившиеся в разные месяцы.

43.

4. О каких событиях говорят:
• «Как гром среди ясного неба»
• «Когда рак на горе свистнет»
5. Постройте дерево возможных вариантов
для задачи:
Сколько трехзначных чисел можно
составить из чисел 1, 3, 5 ?