Похожие презентации:
Математические основы криптографии
1.
МАТЕМАТИЧЕСКИЕ ОСНОВЫКРИПТОГРАФИИ
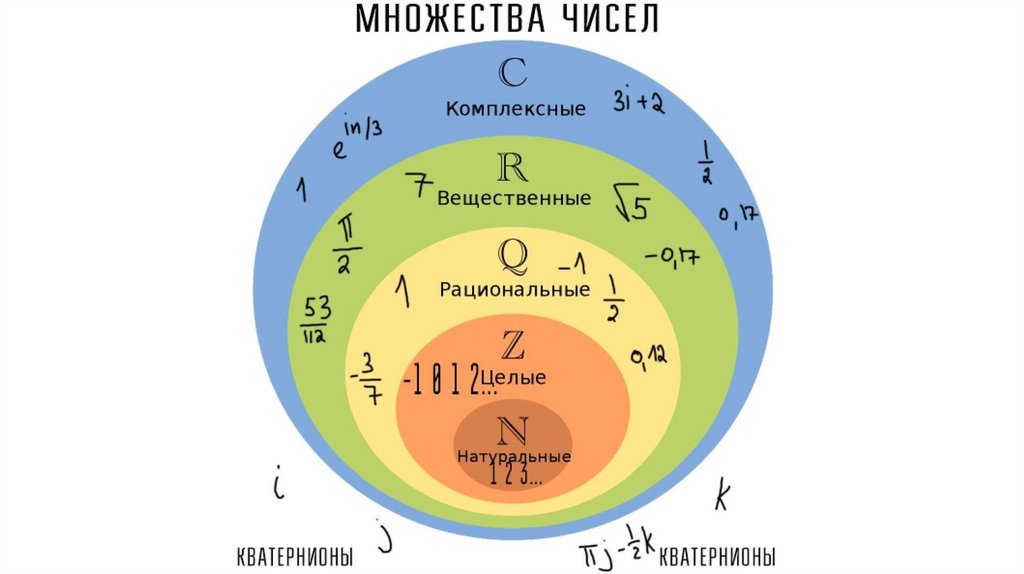
МНОЖЕСТВА
ГРУППЫ
КОЛЬЦА
ПОЛЯ
2.
МНОЖЕСТВА3.
4.
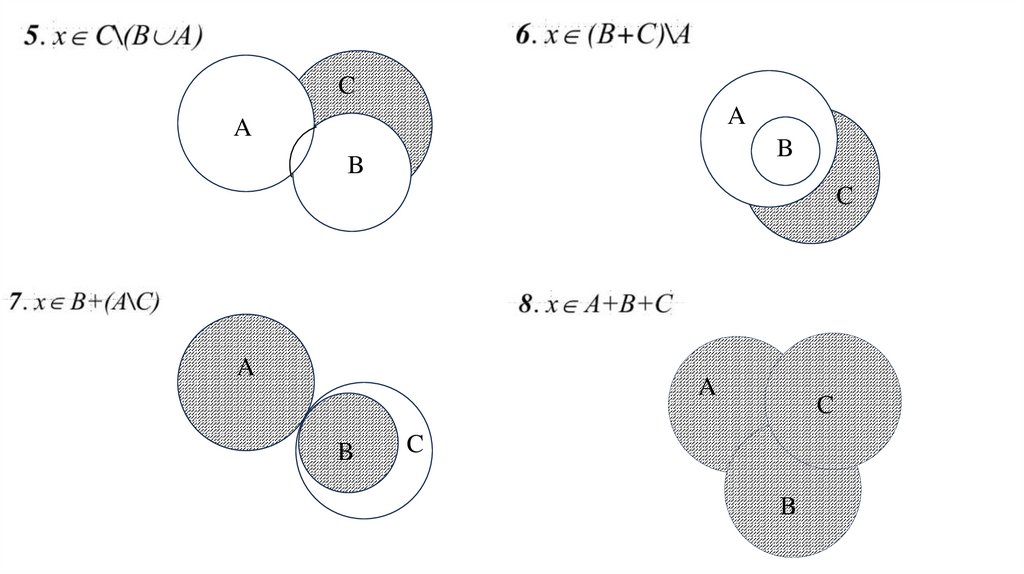
5.
6.
7.
8.
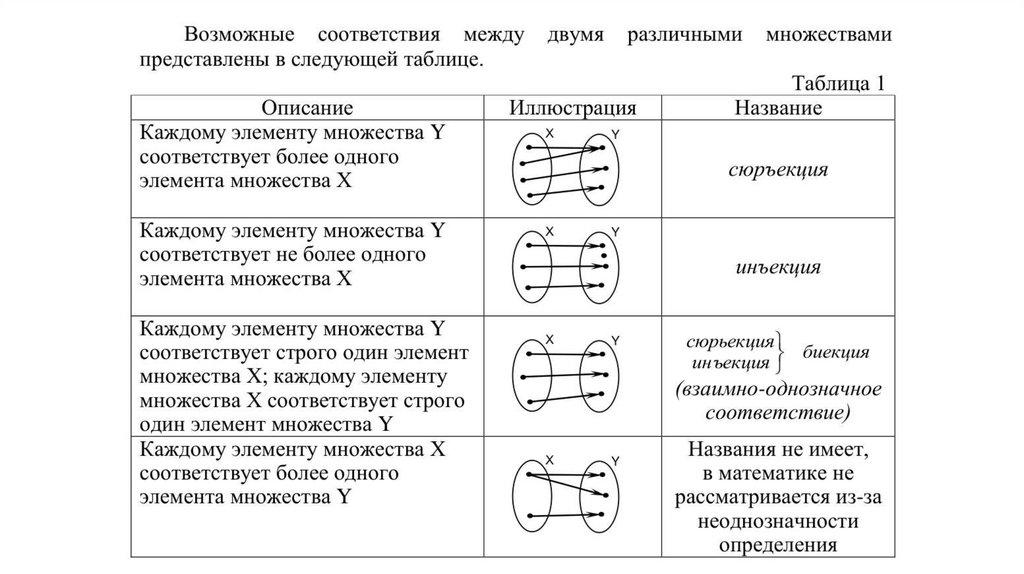
Определение. Если каждому элементу x∈X поставлен в соответствиеединственный элемент y∈Y, то такое соответствие называется отображением
множества Х в множество Y. Т.е., каждому элементу х соответствует только
один элемент y.
9.
10.
11.
12.
Алгебраические структуры: группыМножество G с алгебраической операцией * называется группой, если
выполняются следующие условия:
1) операция * в G ассоциативна: а*(b*с) = (а*b)*с Ɐа,b G;
2) в G существует нейтральный элемент а* = *а = а Ɐа G;
3) для каждого элемента а G существует обратный ему элемент а 1 G:
а*а 1 = а 1 *а
Если операция * коммутативна (ab = ba, a+b = b+a), то группа называется
коммутативной, или абелевой.
Относительно операции сложения группами являются множества Z, Q, R.
Относительно операции умножения группами являются множества Q\{0} и R\{0}.
В группах по сложению нейтральный элемент называют нулем, а обратный элемент
а 1 противоположным ( а).
В группах по умножению нейтральный элемент называют единицей и обозначают е,
для обратного элемента а 1 название и обозначение сохраняется.
13.
Алгебраические структуры: кольцаМножество K на котором заданы две операции сложение (+), и умножение (•),
называется кольцом, если:
1) относительно операции сложения множество К коммутативная группа, т е.
а) операция сложения коммутативна: a+b = b+a Ɐa,b К;
б) операция сложения ассоциативна: a+(b+c) = (a+b)+c Ɐa,b,c К;
в) существует нулевой элемент a+ = +a = a
Ɐa К;
г) для каждого элемента a К существует ( a) К: a+( a) = ( а)+а = ;
2) операция умножения в множестве К ассоциативна:
a⋅(bc) = (ab)⋅c
Ɐa,b,c К;
3) операции сложения и умножения связаны законами дистрибутивности:
(a+b)⋅c=a⋅c+b⋅c, c⋅(a+b)=c⋅a+c⋅b Ɐa,b,c К;
Если операция умножения коммутативна: a⋅b = b⋅a, то кольцо называется
коммутативным. Если для операции умножения существует единичный элемент
a⋅e = e⋅a = a, то говорят, что кольцо К есть кольцо с единицей.
Кольцами являются множества целых, рациональных, действительных чисел (Z, Q, R).
14.
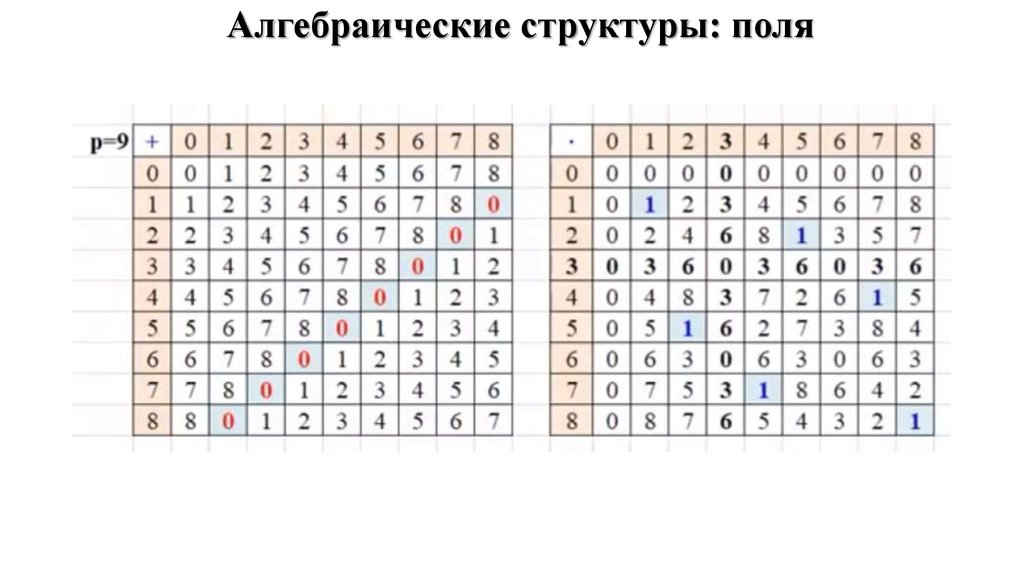
Алгебраические структуры: поляМножество П, на котором заданы две операции: сложение (+) и умножение
называется полем, если выполняются следующие условия:
1) П — коммутативное кольцо с единицей e ;
2) для каждого элемента a П (а ), существует а 1 П: а⋅а 1 = е.
15.
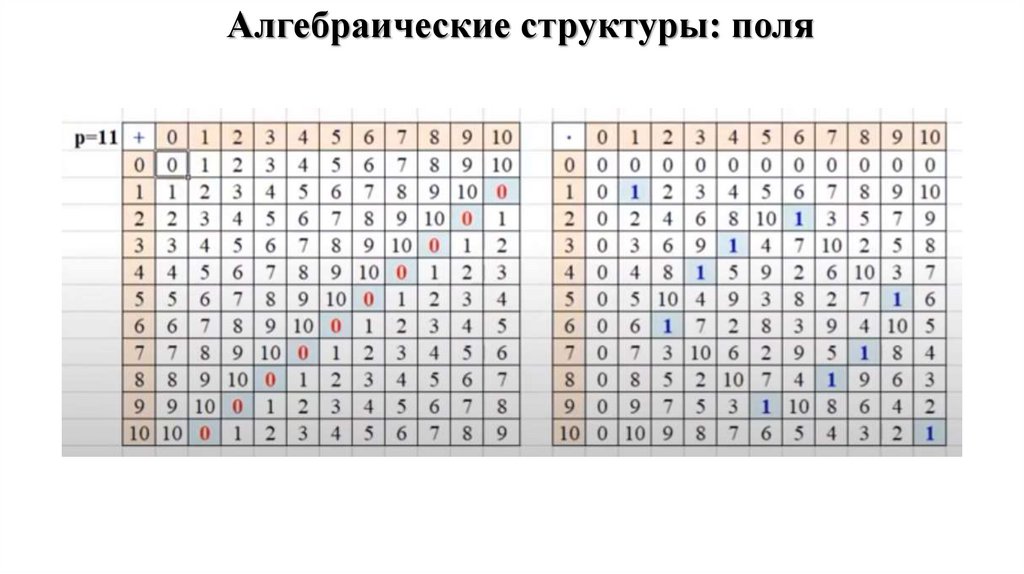
Алгебраические структуры: поля16.
Алгебраические структуры: поля17.
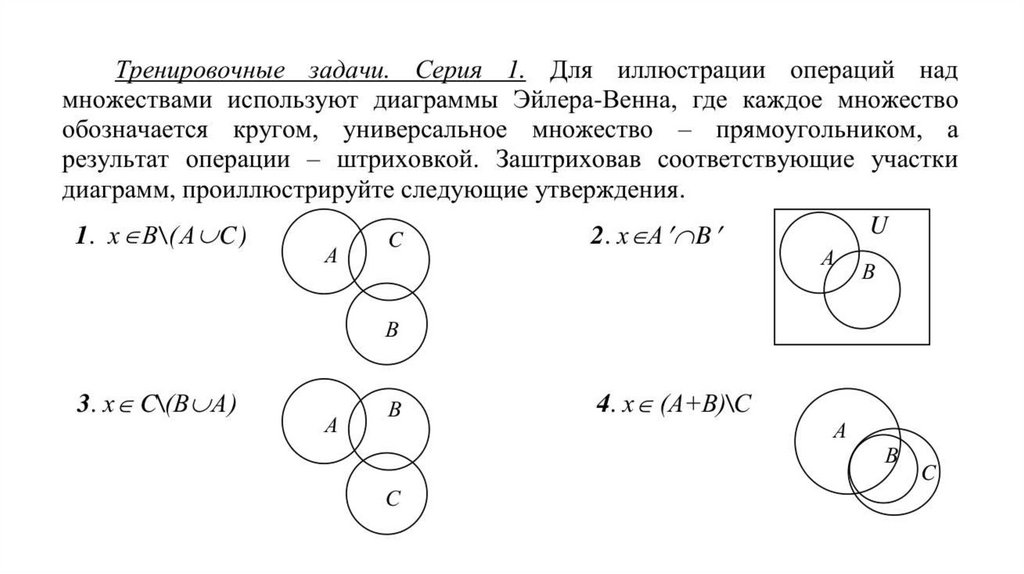
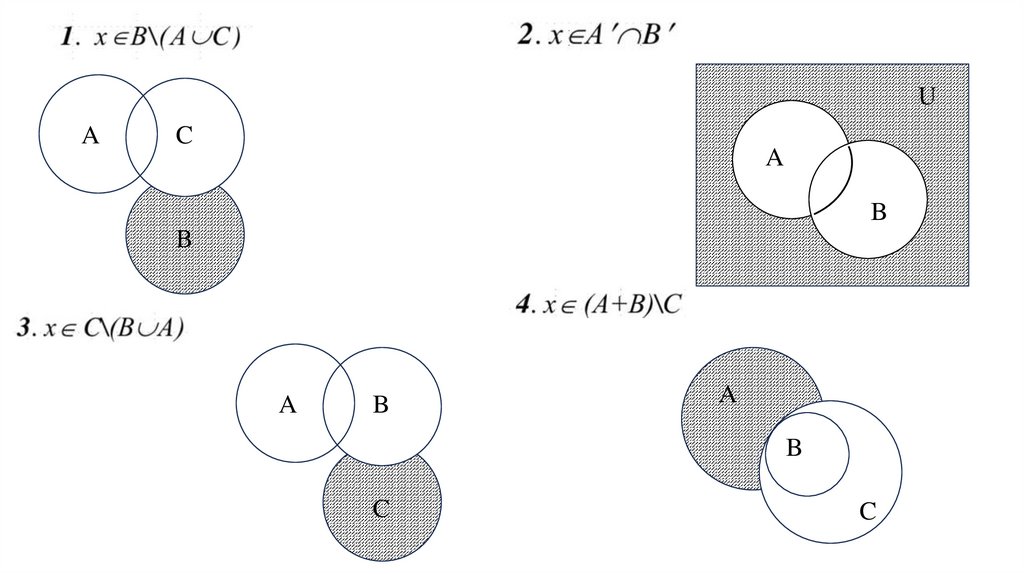
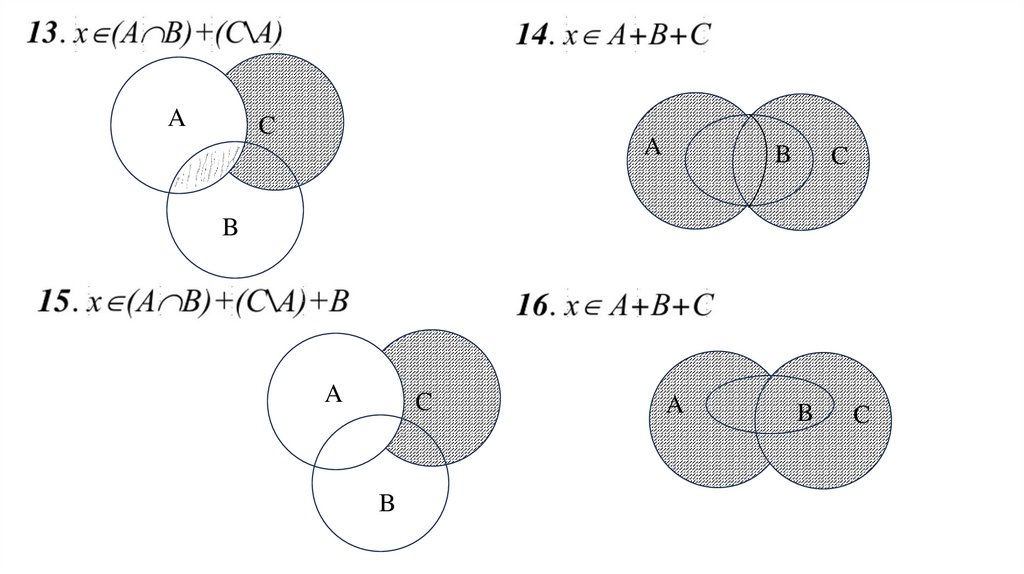
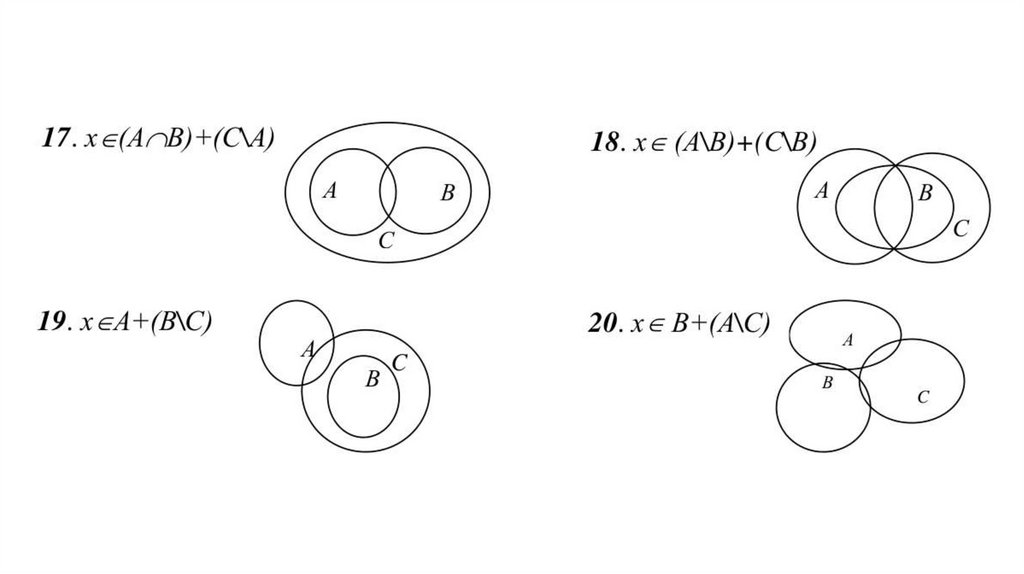
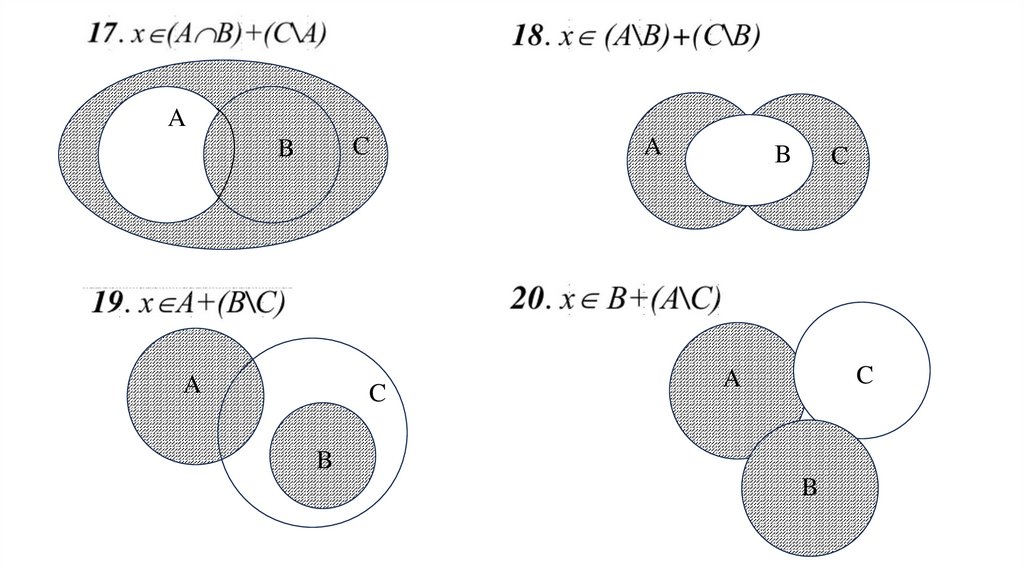
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ18.
Задание 11) Задайте множество цифр, с помощью которых записывается
число:
а) 3254; б) 8797; в) 11000; г) 555555.
2) Задайте множество А описанием:
а) А = {1, 3, 5, 7, 9}; б) А = {–2, –1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};
г) А = {0,1; 0,01; 0,001; 0,0001; …};
д) А = {1/2, 2/3, 3/4, 4/5, … }.
3) Задание с выбором ответа. Даны множества:
М = {5, 4, 6}, Р = {4, 5, 6}, Т = {5, 6, 7}, S = {4, 6}.
Какое из утверждений неверно?
а) М = Р.
б) Р ≠ S.
в) М ≠ Т.
г) Р = Т.
19.
Задание 21. Запишите на символическом языке следующее
утверждение:
а) число 10 – натуральное;
б) число – 7 не является натуральным;
в) число – 100 является целым;
г) число 2,5 – не целое.
2. Верно ли, что:
а) – 5 N;
б) – 5 Z;
в) 2,45 Q?
3. Верно ли, что:
а) 0,7 {х | х2 – 1 < 0};
б) – 7 {х | х2 + 16х ≤ – 64}?
20.
Задание 31. Даны множества:
А = {10}, В = {10, 15}, С = {5, 10, 15}, D = {5, 10, 15, 20}.
Поставьте вместо … знак включения ( ⊂ или ⊃) так,
чтобы получилось верное утверждение:
а) А … D; б) А … В; в) С … А; г) С … В.
2. Даны три множества А = {1, 2, 3, …, 37}, В = {2, 4, 6, 8, …},
С = {4, 8, 12, 16, …, 36}.
Верно ли, что:
а) А ⊂ В;
б) В ⊂ С;
в) С ⊂ А;
г) С ⊂ В?
21.
Задание 41. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11},
С = {5; 11}.
Найдите: 1) А∩В; 2) А∩С; 3) С∩В.
2. Даны множества: А – множества всех натуральных чисел,
кратных 10, В = {1; 2; 3;…, 41}.
Найдите А∩В.
3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f},
C = {c, e, g, k}. Найдите (А∩В)∩С.
22.
Задание 51. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f},
C = {c, e, g, k}.
Найдите (АUВ)UС.
23.
24.
UA
C
A
B
B
A
B
A
B
C
C
25.
26.
CA
A
B
B
C
A
A
B
C
C
B
27.
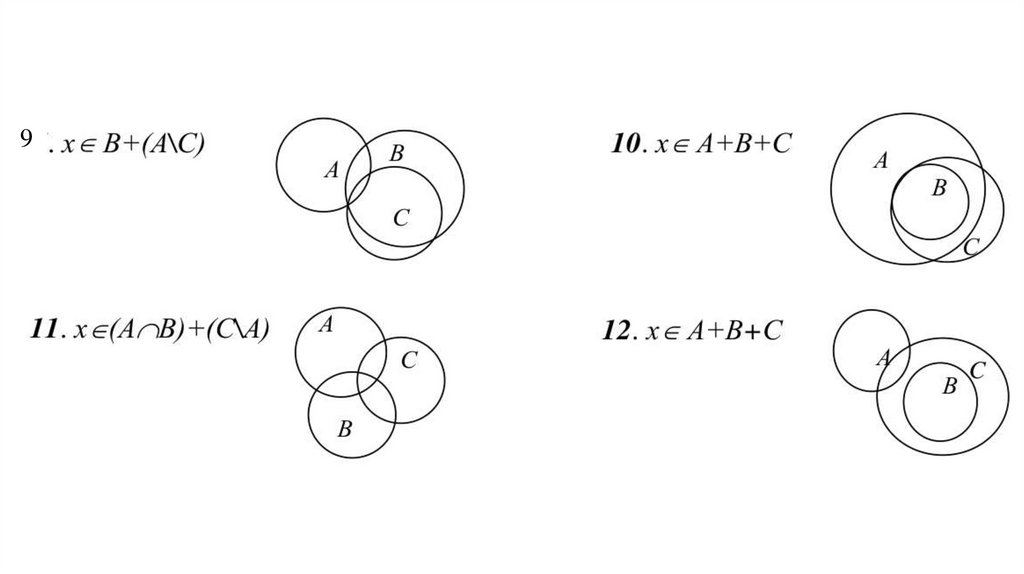
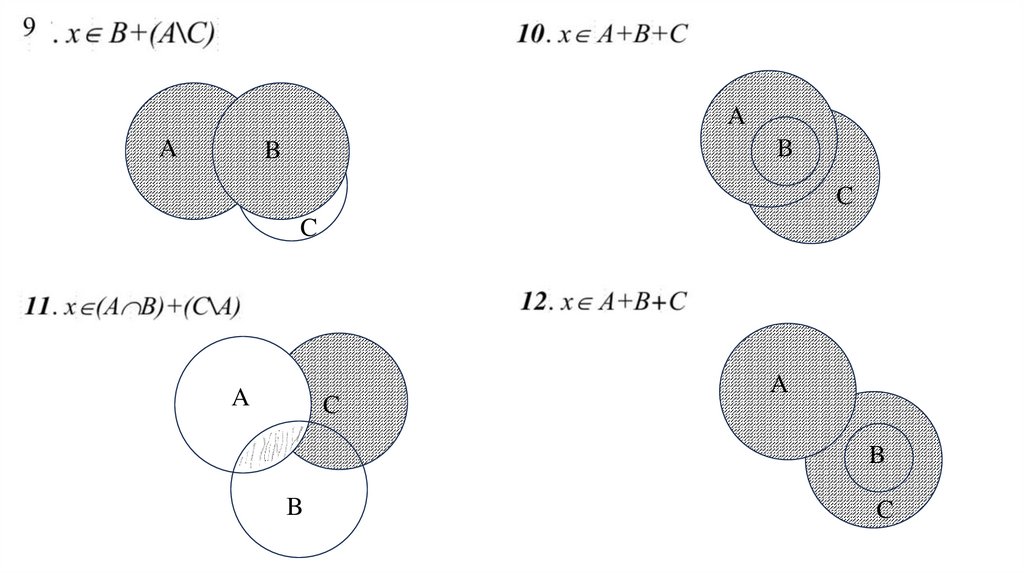
928.
AA
B
B
C
C
AA
C
A
B
B
C
29.
30.
AAC
A
B
C
B
AA
C
B
A
B
C
31.
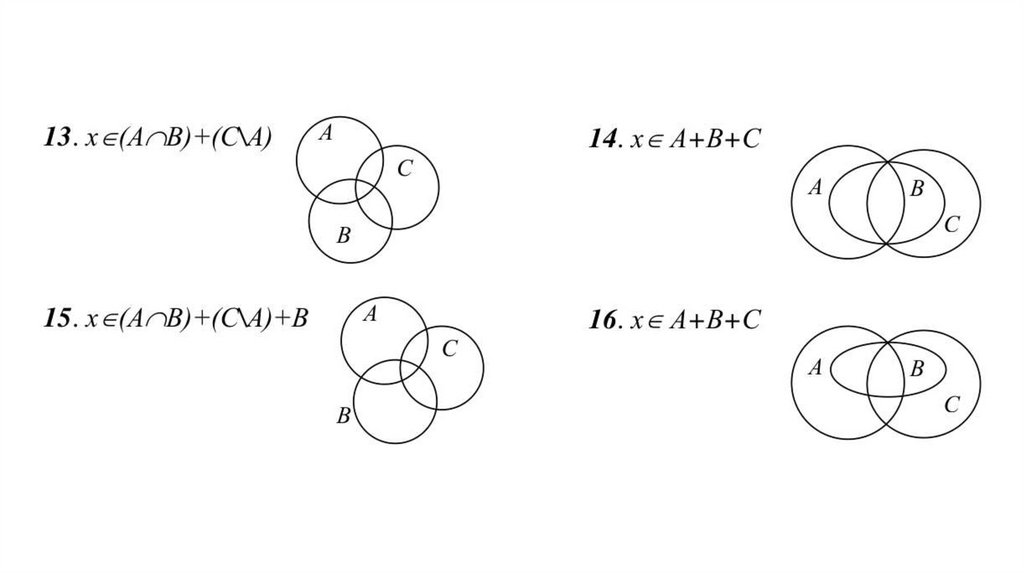
32.
AC
B
A
C
A
B
C
C
A
B
B


















 Математика
Математика