Похожие презентации:
Основы математического анализа
1.
Основыматематического
анализа
Зарубежное регионоведение
1 курс
Сафонова Татьяна Евгеньевна, к.ф.-м.н., доцент
2. Литературв
• Дискретная математика.Курс лекций / И.А. Палий. М.:Эксмо, 2008.
• Дискретная математика. Курс лекций и практических
занятий/ С.Д. Шапорев. СПб.:БХВ-Петербург, 2007.
• Учебно-методическое пособие по математике.
Математическая логика. Дискретная математика.
Линейная алгебра / Под ред. А.Н. Данчула. М.: Изд-во
РАГС, 2004.
• Кремер Н.Ш. Высшая математика для бакалавриата
экономических специальностей. М.: Юрайт, 2014.
2
3. Элементы линейной алгебры
Алгебраматриц
4. Матрица
• Матрица A размера m n –таблица чисел, содержащая m
строк и n столбцов.
• Amn
4
5.
• Элемент матрицы A, находящийся в i-ойстроке и j-ом столбце – aij.
Am n=[aij]m n
a11
a 21
A
...
a m1
a12
a 22
...
am2
... a1n
... a 2 n
... ...
... a mn
5
6.
• Матрица, в которойимеется только одна
строка, – векторстрока
A a11 a11 ... a1n
• Матрица, в которой
есть только один
столбец, – векторстолбец
a11
a 21
A
a m1
6
7. Квадратная матрица
• Матрица, в которой число строк равночислу столбцов, – квадратная матрица n-го
порядка
a11 a12
a21 a22
A
...
...
an1 an 2
... a1n
... a2 n
... ...
... ann
7
8. Диагональная матрица
• Диагональная матрица – квадратная матрица,у которой все элементы, не принадлежащие
главной диагонали, равны нулю
• Главня диагональ матрицы – множество ее
элементов, у которых номер строки равен
номеру столбца
a11 0
0 a22
A
... ...
0
0
0
... 0
... ...
... ann
...
8
9. Единичная матрица
• Единичная матрица –диагональнаяматрица, у которой все элементы,
принадлежащие главной диагонали, равны
единице
1
0
E
...
0
... 0
1 ... 0
... ... ...
0 ... 1
0
9
10.
• Верхней (нижней) треугольной матрицейназывается квадратная матрица
произвольного порядка, все элементы
которой, стоящие под (над) главной
диагональю, равны нулю.
• Нулевой матрицей называется матрица
произвольного порядка, все элементы
которой равны нулю.
10
11. ОПЕРАЦИИ НАД МАТРИЦАМИ
1112. Транспонирование матрицы
• Результат транспонирования матрицыразмера m n – матрица размера n m,
столбцы которой являются строками
исходной матрицы и записаны в том же
порядке.
• B =AT
[bij]n m =[aji]m n
12
13. Умножение матрицы на число
• Результат умножения матрицы размераm n на число – матрица того же размера,
все элементы которой равны
соответствующим элементам исходной
матрицы, умноженным на это число.
Bmn= Amn
[bij]mn =[ aij]mn
13
14. Сложение матриц
• Результат сложения двух матрицодинакового размера m n – матрица того
же размера, все элементы которой равны
сумме соответствующих элементов
матриц-слагаемых.
Cmn =Amn + Bmn
[cij]mn =[aij+bij]mn
14
15. Вычитание матриц
• Результат вычитания двух матрицодинакового размера m n – матрица того
же размера, все элементы которой равны
разности соответствующих элементов
матриц-слагаемых.
• Cmn =Amn - Bmn
• [cij]mn =[aij - bij]mn
15
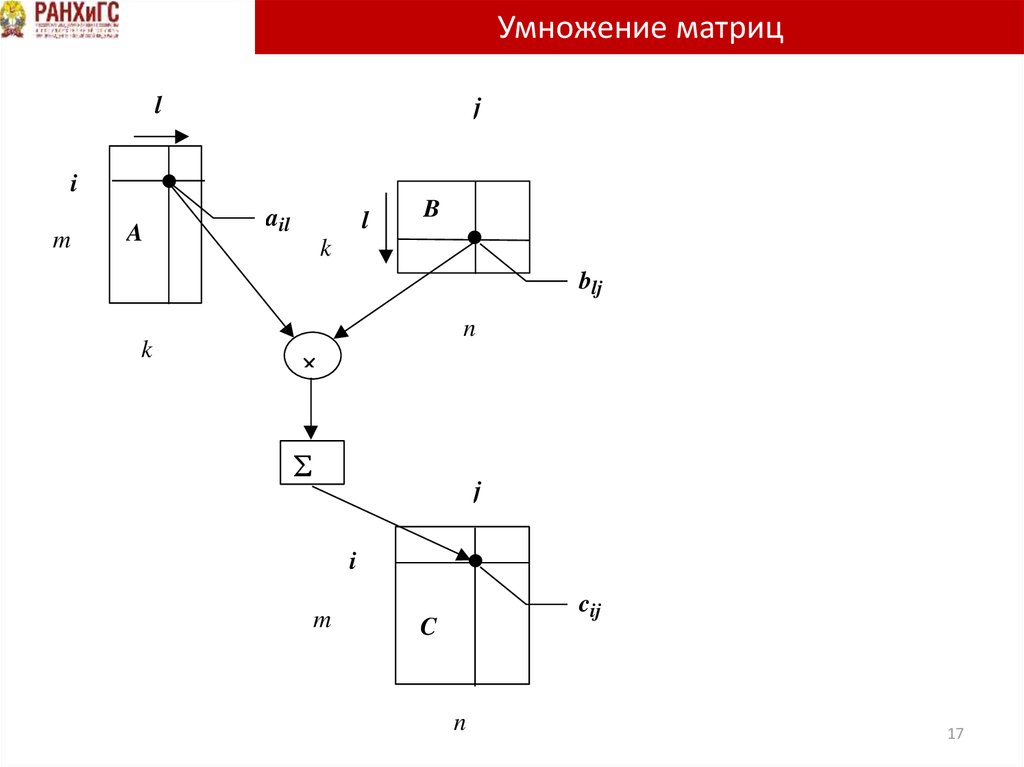
16. Умножение матриц
• Результат умножения матрицы A размераm k на матрицу B размера k n – матрица C
размера m n, каждый элемент которой cij
равен сумме всех попарных произведений
элементов, стоящих на одинаковых местах
в i-ой строке матрицы A и j-ом столбце
матрицы B.
• Cmn =AmkBkn
16
17. Умножение матриц
lj
i
m
ix
A
kk
ail
l
B
A
k
blj
k
n
j
i
m
cij
C
n
17
18. Свойства операций:
1. A+B= B+A
2. (A+B)+C=A+(B+C)
3. (A+B)= A+ B
4. A(B+C)=AB+AC
(A+B)C=AC+BC
5. (AB) = ( A)B = A( B)
6. A(B C)=(AB)C
7. В общем случае AB BA
18
19. ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ
• A – квадратная матрица порядка n, ееопределитель обозначается det(A) или A .
• Если n =1, то A = a11 =a11
• Если n =2, то:
A
a11
a12
a 21
a 22
a11a 22 a12 a 21
19
20. n=3
+20
21.
• Минор Mij элемента aij матрицы A n-гопорядка – определитель матрицы (n-1)-го
порядка, полученной из A вычеркиванием
i–ой строки и j–го столбца.
• Алгебраическое дополнение Aij элемента
aij матрицы A n-го порядка – его минор,
взятый со знаком, определяемым по
правилу шахматной доски
21
22. Разложение определителя по строке (или столбцу):
nA ai1 Ai1 ai 2 Ai 2 ... ain Ain ail Ail
l 1
n
A a1 j A1 j a2 j A2 j ... anj Anj alj Alj
l 1
22
23.
• Квадратная матрица, определителькоторой равен нулю – вырожденная.
23























 Математика
Математика








